结构方程模型(SEM)
# 结构方程模型(SEM)
# 1、作用
结构方程模型(SEM)是一种基于因子分析、线性回归方法、用于分析错综复杂变量之间路径关系的一种模型。与线性回归不一样的是,SEM 是以量表为单位的,也就是将量表通过因子分析降维成 1 个主成分(多个变量转化为一个变量),再进行路径分析。
# 2、输入输出描述
输入:建立因子对应的路径关系,一般要求输入数据为定量数据。
输出:各因子作用的路径关系或是否成立。
# 3、案例示例
案例:研究“幸福感”的影响因素,有四个因子可能对幸福感有影响,他们分别是:经济水平、受教育程度、情感支持。而每个因子又由多个变量组成,其中经济水平包括(衣、食、住、行)、情感支持包括(父母关心、同学相处、老师指导)、受教育程度包括(学校资源、补课程度)、幸福度包括(满足感、开心感),通过路径分析可以得到这四个变量如右图所示路径关系作用于幸福感。
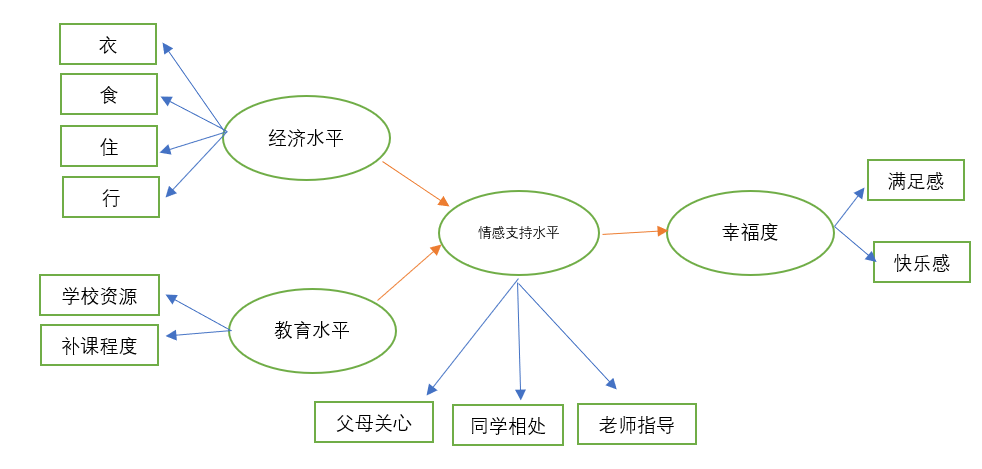
# 4、案例数据
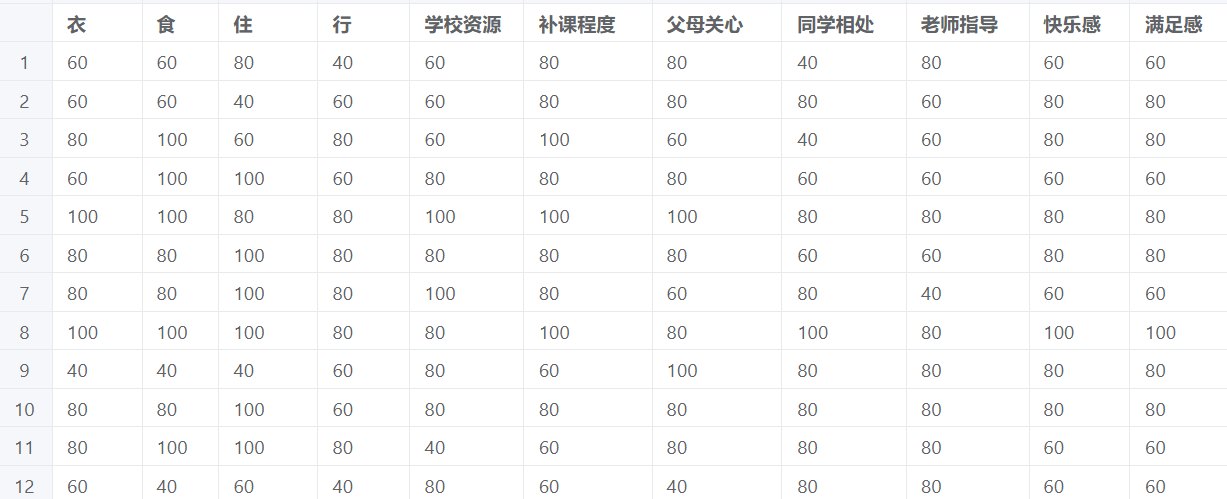
结构方程模型(SEM)案例数据
模型输入为建立因子对应的路径关系,一般要求输入数据为定量数据。其中衣食住行为一个因子,学校资源和补课程度为一个因子,父母关心、同学相处和老师指导为一个因子,快乐感和满足感为一个因子。在给出因子的路径关系,这是由调查或者询问专家获得的。# 5、案例操作
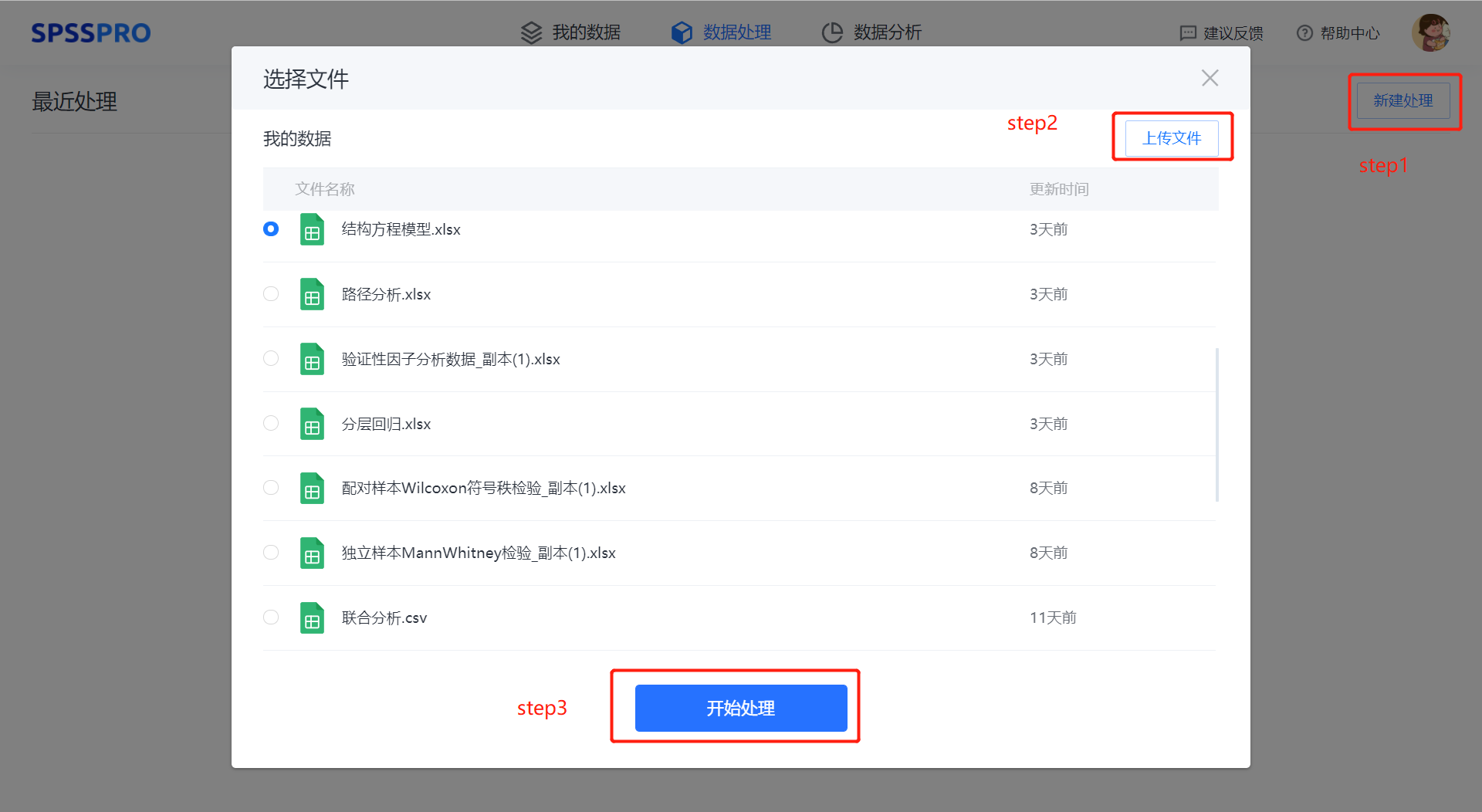
Step1:新建分析;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;
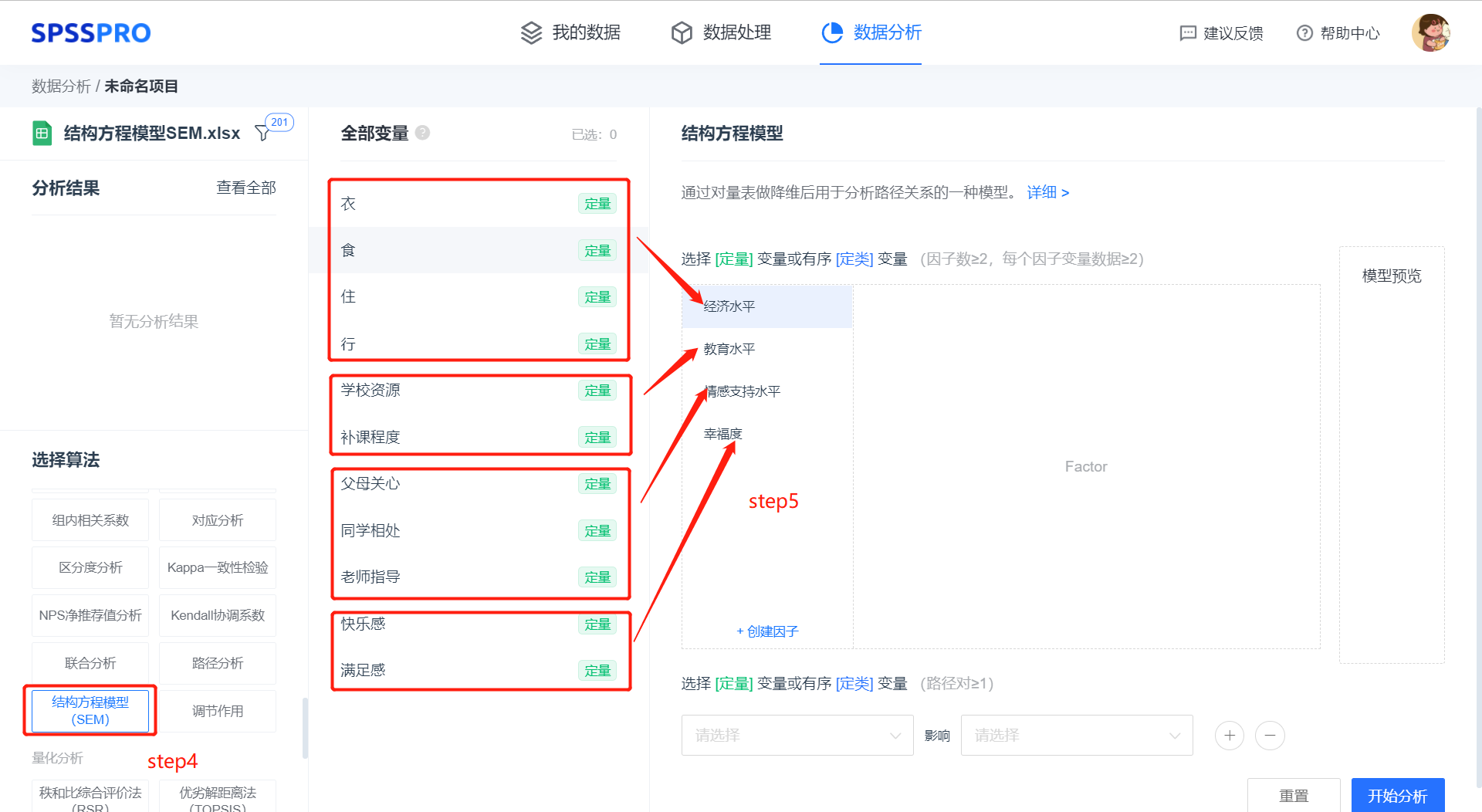
Step4:选择【结构方程模型】;
Step5:查看对应的数据数据格式,要求把各因子所包含的变量进行整合;

Step6:【结构方程模型】要求按照初步假设出模型中各变量的相互关系,绘制成一张清晰的路径分析图;
Step7:点击【开始分析】,完成全部操作。
# 6、输出结果分析
输出结果 1:模型路径图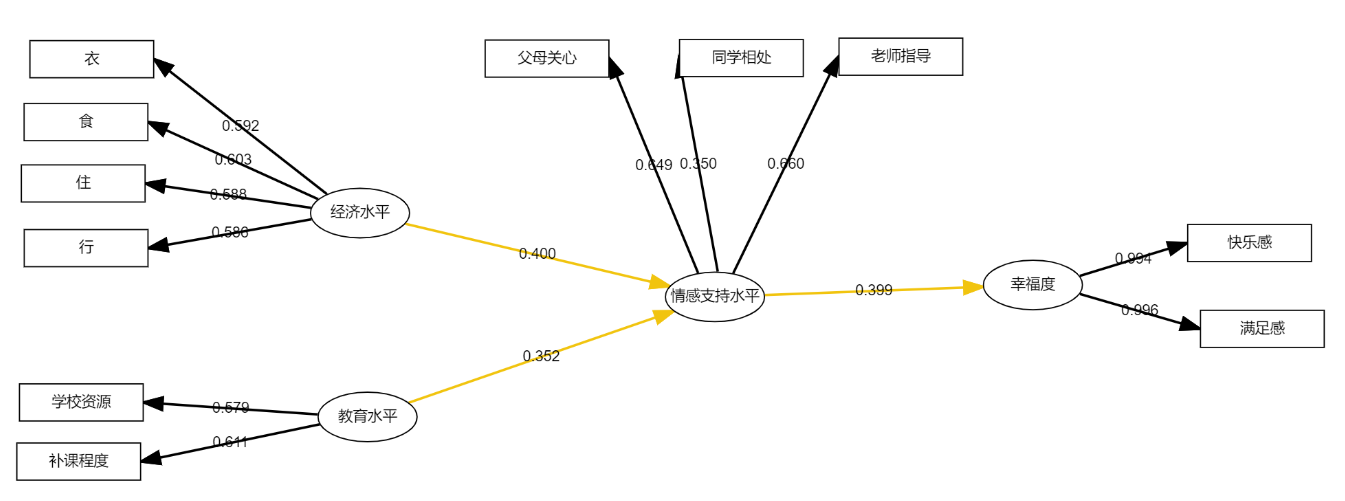
图表说明:上表展示了带权结构路径图,主要包括模型的标准化系数,用于分析结构路径影响关系情况。
输出结果 2:因子载荷系数表
图表说明:注意:在同一因子测量关系时,第一项会被作为参照项,因此不会呈现p 值等。
基于食(显著性 p 值为 0.000***)、住(显著性 p 值为 0.000***)、行(显著性 p 值为 0.000***)的水平上呈现显著性,则拒绝原假设,同时其标准载荷系数均大于 0.4,可以认为其有足够的方差解释率表现各变量能在同一因子上展现。
基于补课程度(显著性 p 值为 0.000***)的水平上呈现显著性,则拒绝原假设,同时其标准载荷系数均大于0.4,可以认为其有足够的方差解释率表现各变量能在同一因子上展现。
基于老师指导(显著性 p 值为 0.000***)的水平上呈现显著性,则拒绝原假设,同时其标准载荷系数均大于0.4,可以认为其有足够的方差解释率表现各变量能在同一因子上展现。
基于满足感(显著性 p 值为 0.000***)的水平上呈现显著性,则拒绝原假设,同时其标准载荷系数均大于0.4,可以认为其有足够的方差解释率表现各变量能在同一因子上展现。
输出结果 3:模型回归系数表
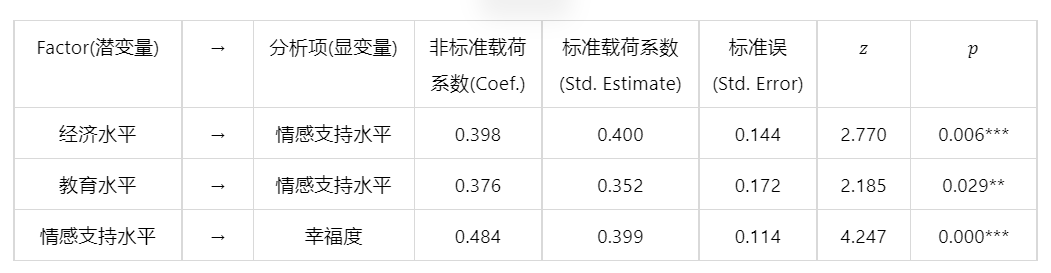
图表说明:基于配对项经济水平->情感支持水平,显著性 P 值为 0.006***,水平上呈现显著性,则拒绝原假设,因此此路径有效,其影响系数为 0.4。
基于配对项教育水平->情感支持水平,显著性 P 值为 0.029**,水平上呈现显著性,则拒绝原假设,因此此路径有效,其影响系数为 0.352。
基于配对项情感支持水平->幸福度,显著性 P 值为 0.000***,水平上呈现显著性,则拒绝原假设,因此此路径有效,其影响系数为 0.399。
输出结果 4:模拟拟合指标 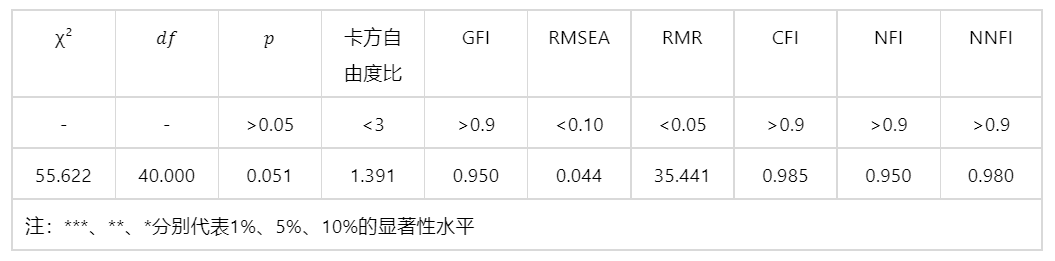
图表说明:上表展示了模型的拟合指标,可以适当选择一些指标进行评价,若所有指标均不满足,可以考虑根据输出 1 对路径进行删除或者重构。
● 卡方和自由 df 度主要用于比较多个模型,卡方值越小越好,自由度反映了模型的复杂程度,模型越简单,自由度越多,反之,模型越复杂,自由度越少。
● GFI(拟合优度指数):主要是运用判定系数和回归标准差,检验模型对样本观测值的拟合程度。其值在 0-1 之间,愈接近 0 表示拟合愈差。CFI≥0.9,认为模型拟合较好。
● RMSEA(近似误差均方根):一般情况下,RMSEA 在 0.08 以下(越小越好)。
● RMR(均方根残差):该指标通过测量预测相关和实际观察相关的平均残差,衡量模型的拟合程度。如果 RMR < 0.1,则认为模型拟合较好。
● CFI(比较拟合指数):该指数在对假设模型和独立模型比较时,其值在 0-1 之间,越接近 0 表示拟合越差,越接近 1 表示拟合越好。一般情况,CFI≥0.9,认为模型拟合较好。
● NNFI(非规范拟合系数)和 CFI(比较拟合指数) :其值越大越好,所拟合的模型表现较好。
结果分析:由上表可知,大部分指标都满足要求,说明拟合的模型表现较好。
输出结果 5:路径节点协方差关系表 
图表说明: 协方差表格分析了模型中没有入度的节点(即没有箭头指向它的节点),用于分析路径节点之间的关联性。
结果分析:由上表可知, 经济水平与情感支持水平的协方差关系呈现显著性,标准化系数为 0.504,有中等的关联性,建议加入路径关系进行分析。
# 7、注意事项
- 结构方程模型 SEM 构建前需要保障好测量关系的质量,建议结构方程模型 SEM 分析之前先进行探索性因子分析和验证性因子分析,确保测量显变量与潜变量关系良好后再进行 SEM 分析;
- 结构方程的路径关系可以用来反驳一个表明变量之间存在因果关系的模型;但是,它不能用来证明变量之间存在因果关系。
- 结构方程模型相比起路径分析,多了一个因子测量模型。当我们想对难以描述的概念建立路径时,比如想要建立”生活习惯->健康“这个路径,其中两个概念都很难描述,我们可以用饮食均衡、坚持运动等等指标来反映生活习惯,用心率、血压、体温等等指标来反映这个概念;
# 8、模型理论
结构方程模型是因子分析和路径分析的结合,它的初衷是针对潜变量之间关系进行建模。当我们面对一个难以描述概念时,就需要找到符合该概念下的指标。比如健康这个概念,我们很难描述,就会用心率、血压、体温等等指标来反映这个概念。当我们有了一定的研究后,从理论上已经分析出了多个难以描述的指标之间的关系,就需要用到结构方程模型,其步骤如下:
步骤 1 模型设定
研究者根据专业知识,通过推论何假设形成一个关于变量之间相互关系(常常是因果关系)的模型,这个模型也可以用路径表明制定变量之间的因果关系。
步骤 2 模型评价
评价模型样本数据拟合程度,否具有统计学意义,并且是否能够很好的与专业知识相吻合。
步骤 3 模型修正
当尝试模型出现不能拟合观察数据的情况时,就需要将模型进行修正。
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 吴兵福. 结构方程模型初步研究[D].天津大学,2006.
