多维尺度分析
# 1、作用
多维尺度分析可在低维空间反应多维因素的关系,利用平面距离反映对象之间的相似程度,能够识别影响事务相似性的潜在因素,在市场研究时能看清市场环境、竞争关系,效用巨大。
# 2、输入输出描述
输入:两项及以上的定量数据。
输出:空间感知图的距离反映对象之间差异程度(距离越远代表差异性越大)。
# 3、案例示例
案例:现有 42 个消费者对 15 种早餐进行评分,通过多维尺度分析来研究 15 种早餐的受欢迎程度结构(按变量列进行分析)或是 42 个消费者的喜好结构(按样本行进行分析)。
# 4、案例数据
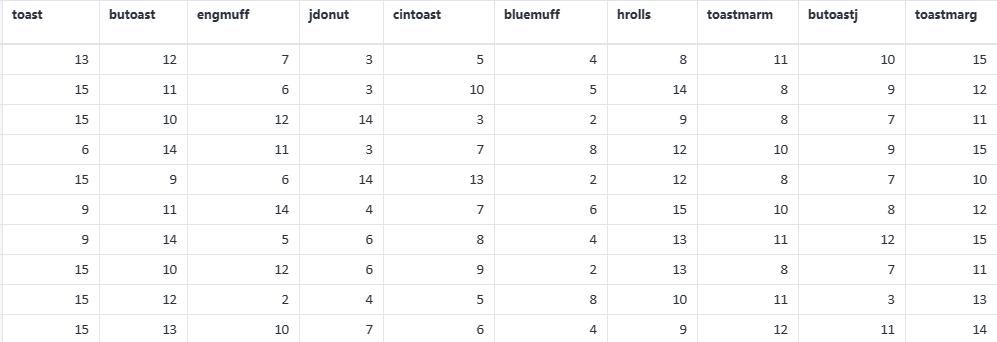
多维尺度分析案例数据
# 5、案例操作
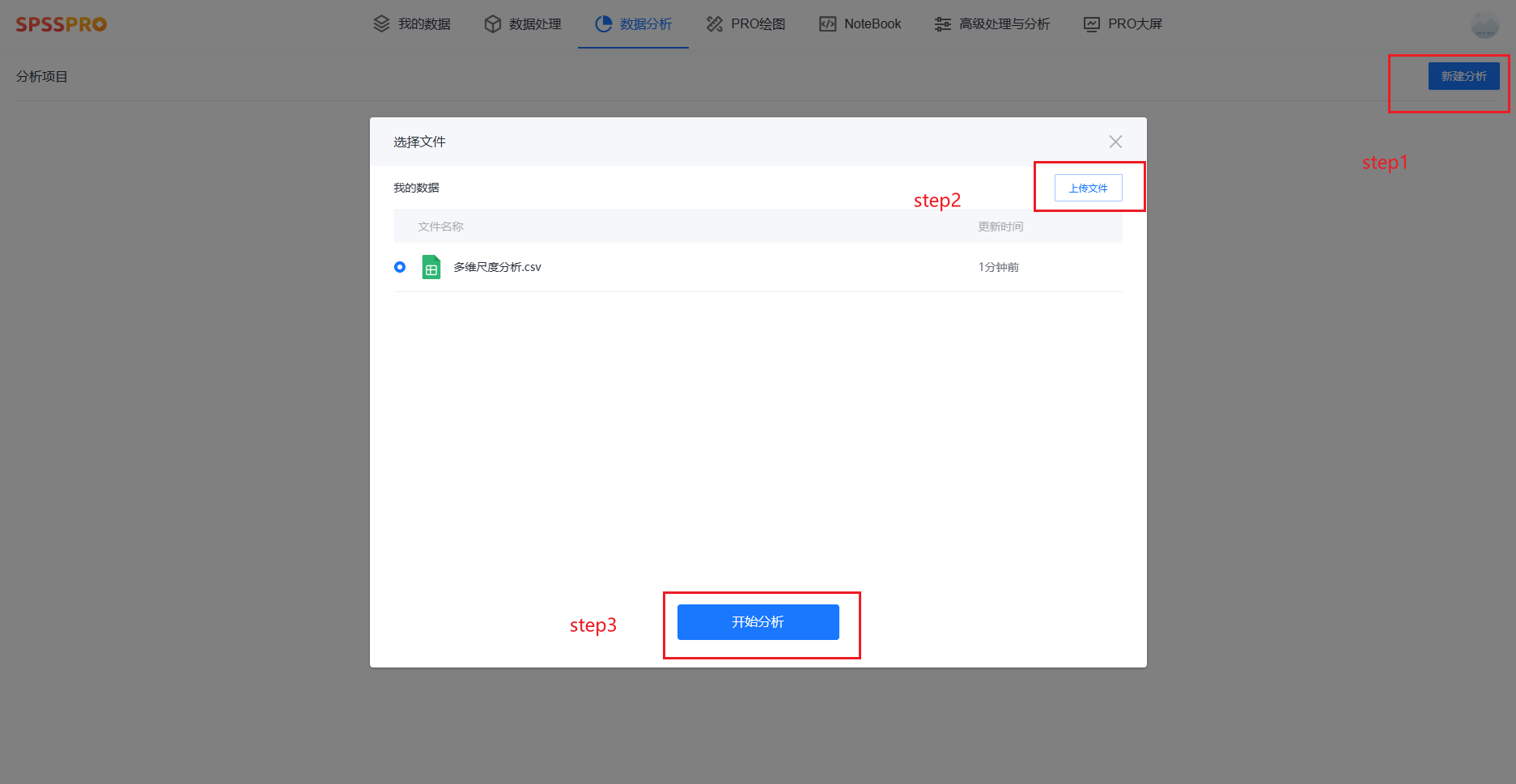
Step1:新建分析;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;
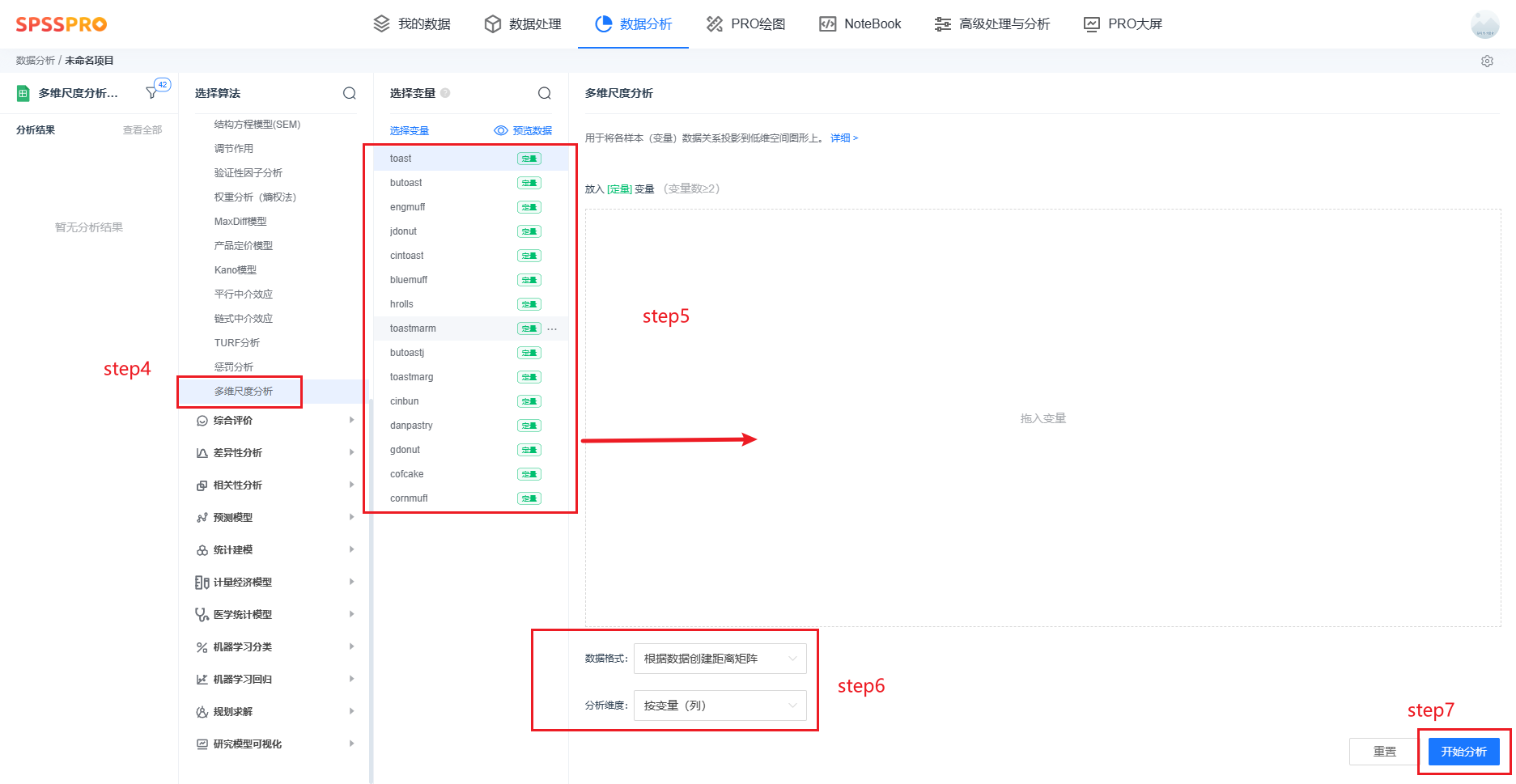
step4:选择【多维尺度分析】;
step5:查看对应的数据数据格式,【多维尺度分析】要求特征序列为至少两项定量变量;
step6:确定参数;
step7:点击【开始分析】,完成全部操作。
# 6、输出结果分析
输出结果 1:距离矩阵 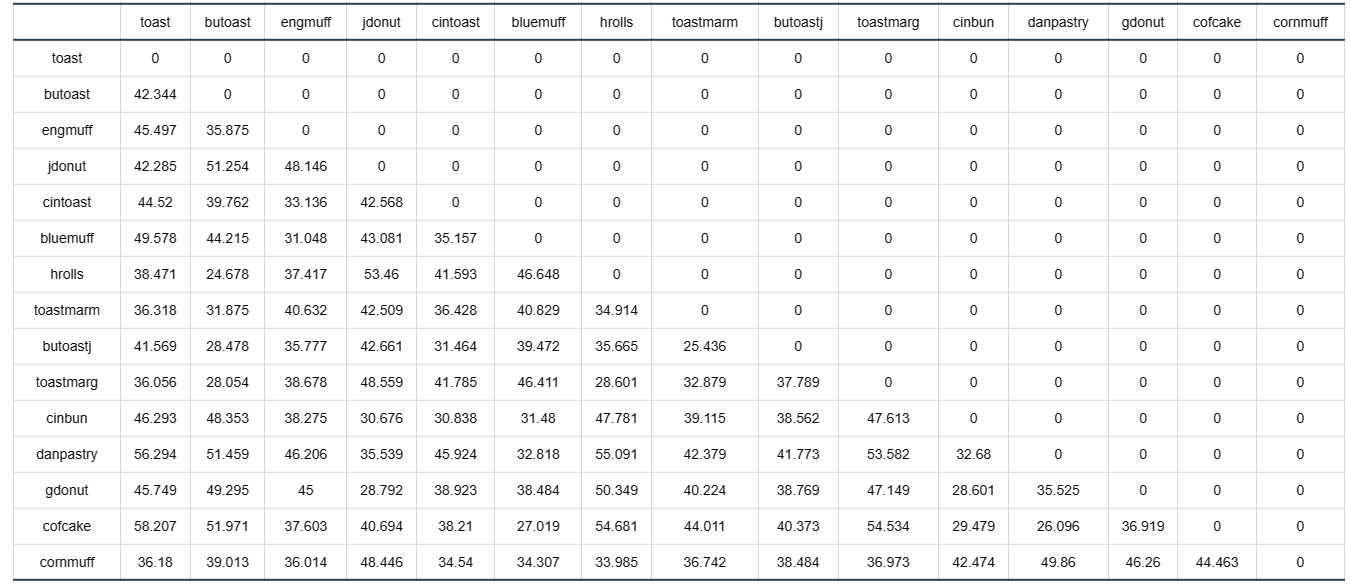
图表说明:上表展示了距离矩阵,其值为两两变量(样本)之间的距离,值越大说明两两变量(样本)之间的差异性越大。
输出结果 2:指标重要度直方图
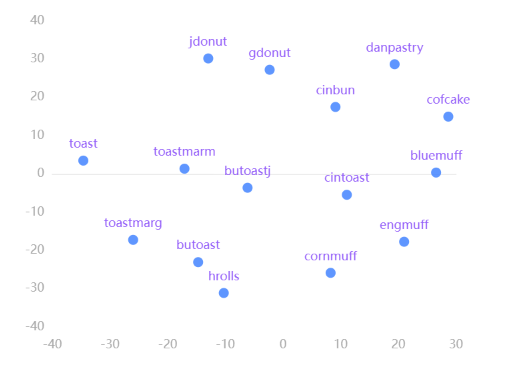
图表说明:上图为根据距离矩阵在低维图形上绘制的各样本(变量)之间差异性。
# 7、注意事项
- 当数据格式为“根据数据创建距离矩阵”:按照变量列进行运算时,是以每列的数据作为一个对象,是求解各列的差异;按照样本行进行运算时,是以每行的数据作为一个对象,然后来求解各行的差异;
- 当数据格式为“数据为距离矩阵”,此时要求上传对称矩阵。
# 8、模型理论
多维尺度分析基本原理是通过某种非线性变换,把高维空间的几何图形转化成低维空间的图形,变换后的图形仍能近似地保持原图形的集合关系。这些点所在的空间是欧几里得空间,可以是二维、三维或多维。它拥有两种输入格式,一种是直接给出距离矩阵,另外一种是通过输入数据计算出啊距离矩阵。
(1)输入数据格式 1:多维尺度分析处理的数据是一般是表示事物之间的接近性的观察数据,比如说拖入的数据就是各个品牌的不相似矩阵,可以通过多维尺度得到各个品牌的空间感知图。
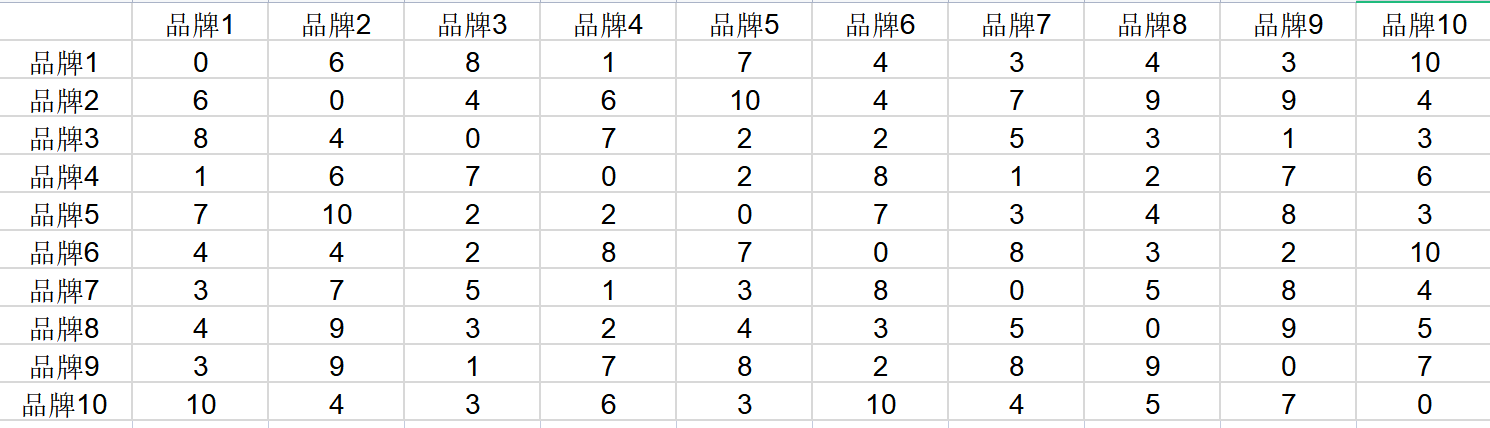
(2)多维尺度分析处理的数据也可以是主观评判的相似性(根据数据创建距离矩阵),目的就是要发现决定多个事物之间距离的潜在维度,用较少的变量对事物之间的差异性作出解释。
比如本例中:有 42 个消费者对 15 种早餐进行评分,先通过多维尺度可以得到各种早餐的距离矩阵,后绘制出低维的空间感知图,即把高维空间的几何图形转化成低维空间的图形。
多维尺度分析算法的计算步骤如下:
计算原始空间中样本点的距离矩阵,以欧式距离为例
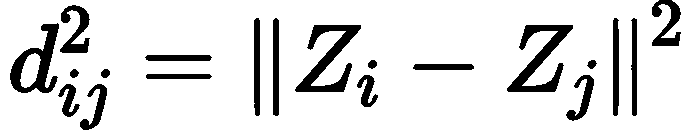
计算内积矩阵 B
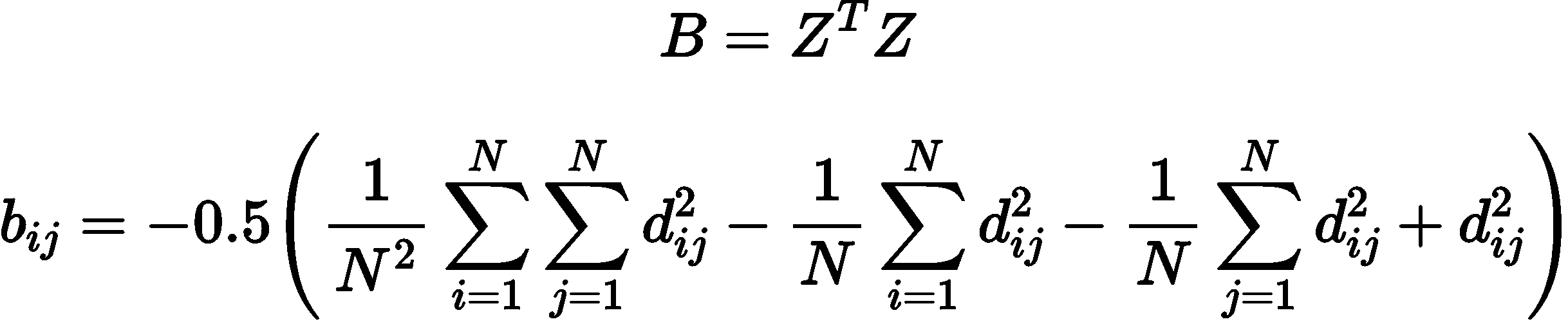
对矩阵 B 进行特征值分解,获得特征值矩阵和特征向量矩阵
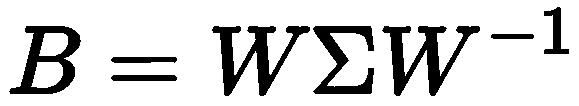
取特征值矩阵最大的前 Z 项及其对应的特征向量,构成最终降维之后的结果
![]()
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 骆文淑, 赵守盈. 多维尺度法及其在心理学领域中的应用[J]. 中国考试, 2005(4):27-30.
