# 联合分析

# 1、作用

联合分析是一种基于调查的统计技术，用于市场研究，有助于确定人们如何评估构成个别产品或服务的不同属性（特征，功能，效益），其目的是确定哪一种属性组合对受访者的选择或决策最有影响力。

# 2、输入输出描述

输入：属性 X 为至少两项或以上的定类变量，属性组合得分 Y 要求为定量变量或有序定类变量。
输出：输出不同属性（特性、功能）相对重要性及最优属性组合。 ​

# 3、案例示例

案例：通过联合分析对几款饮料的属性（口味、价格、容器、品牌）进行评估，并确定哪一种属性组合更受欢迎。

# 4、案例数据

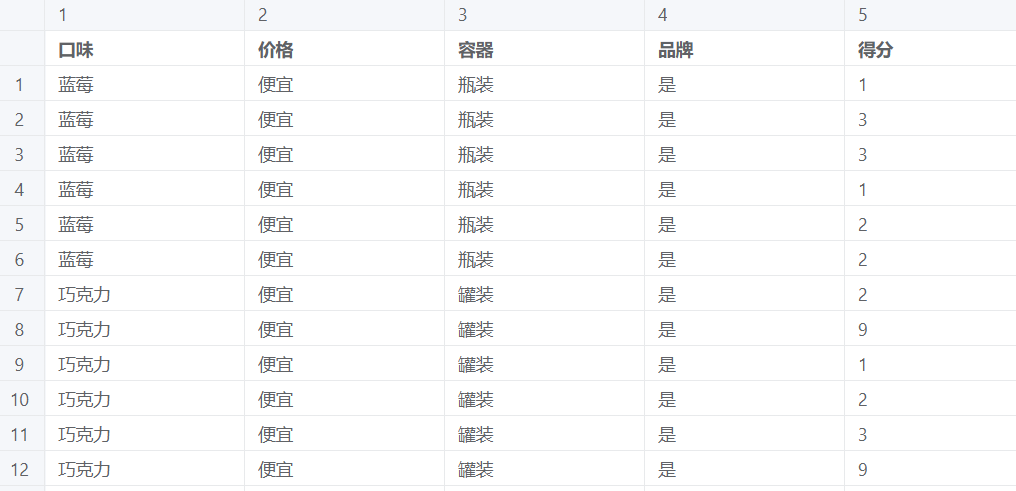
联合分析案例数据

联合分析需要数据为属性 X 为至少两项或以上的定类变量，属性组合得分 Y 要求为定量变量或有序定类变量，需要用特殊的问卷来进行问卷调查得到,问卷数据设计示例（单选题）如下：
现有以下饮料 1，请对该饮品的喜好程度打分（1-9 分）
口味：蓝莓
价格：便宜
品牌：不是
容器：罐装

现有以下饮料 2，请对该饮品的喜好程度打分（1-9 分）
口味：巧克力
价格：便宜
品牌：是
容器：罐装

现有以下饮料 2，请对该饮品的喜好程度打分（1-9 分）
......

# 5、案例操作

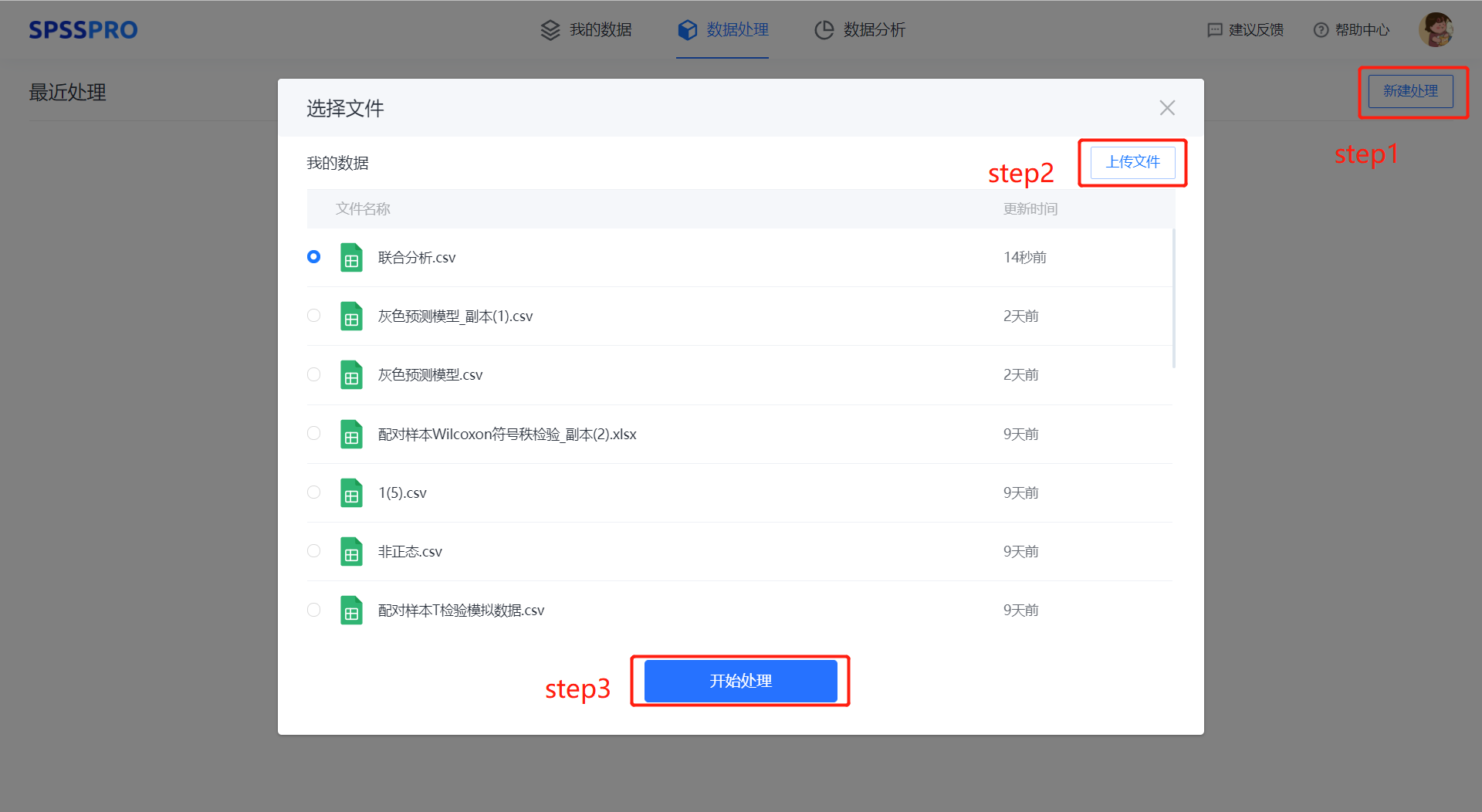
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

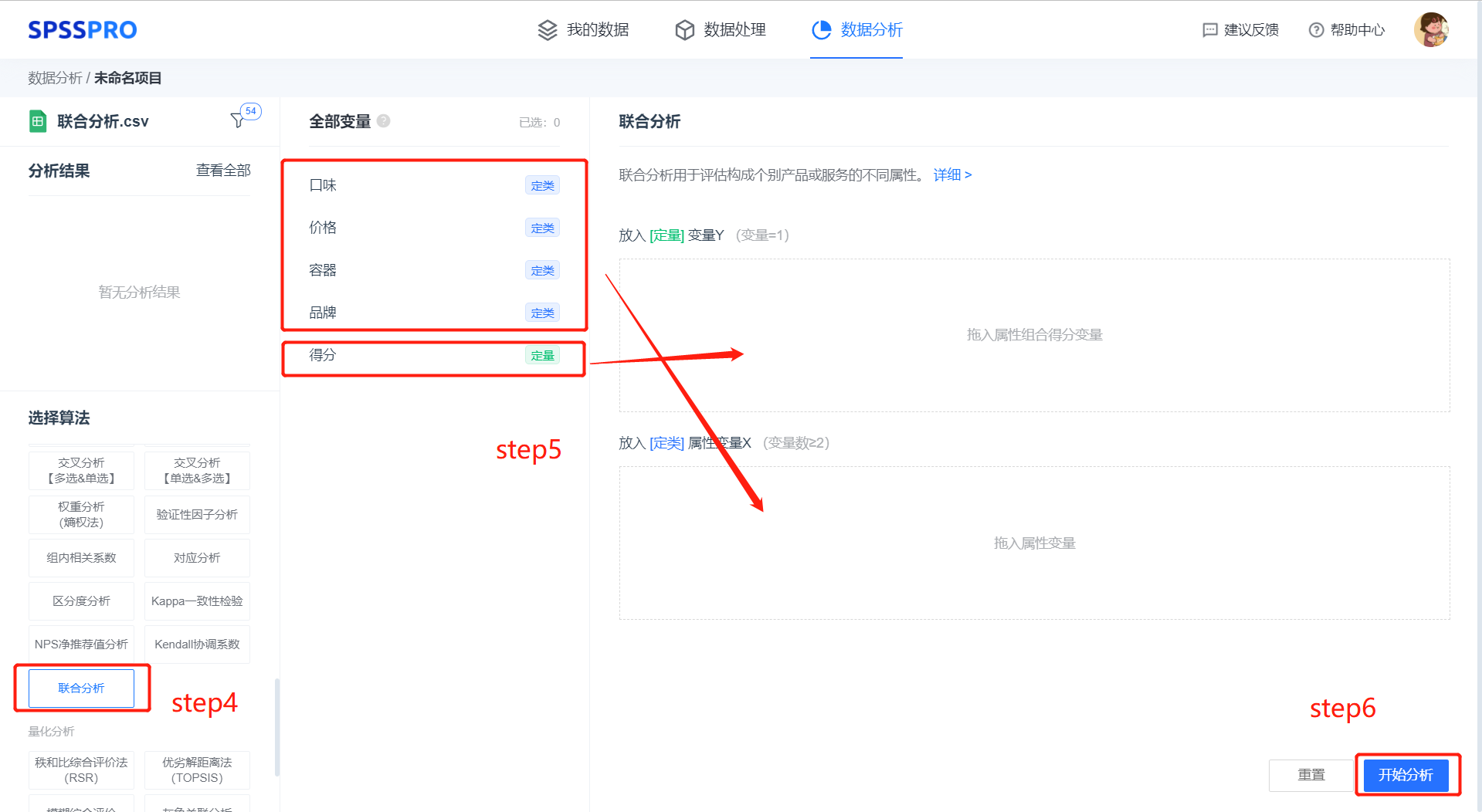
Step4：选择【联合分析】；
Step5：查看对应的数据数据格式，【联合分析】要求属性变量 X 为定类变量，且至少有两项；变量 Y 为定量变量，且只有一项；
Step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：​水平效用模型 ols 参数估计结果表

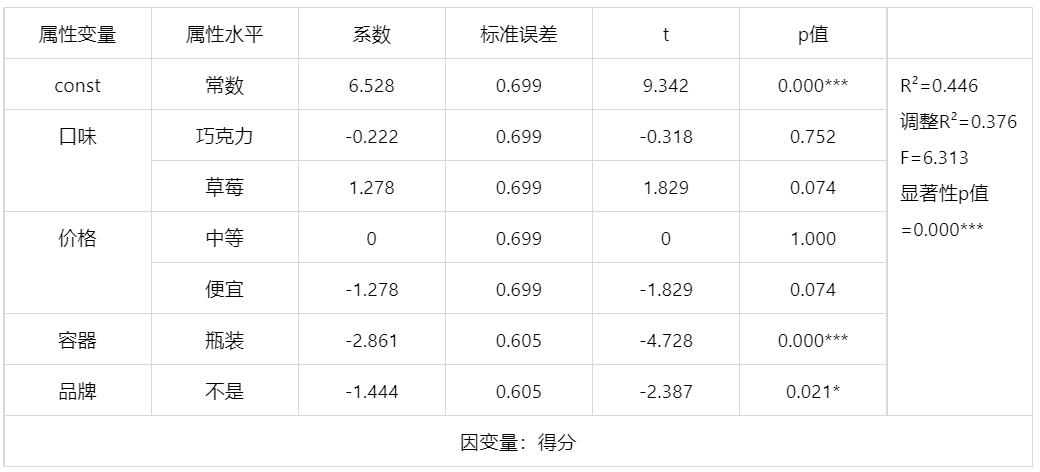
图表说明：上表格展示了水平效用模型的最小二乘估计结果，包括模型的系数、标准误差、t值、P、R²、调整R²等，用于模型的检验。
结果分析：从上表分析可以得到，模型的显著性 p 值为 0.000，在 α=0.05 的水平上呈现显著性，拒绝了回归系数为 0 的原假设，同时模型的拟合优度 R² 为 0.446，模型表现一般，因此模型基本满足要求，可以根据回归系数继续求效用值。​
​
​

输出结果 2​：属性的效用值及重要性

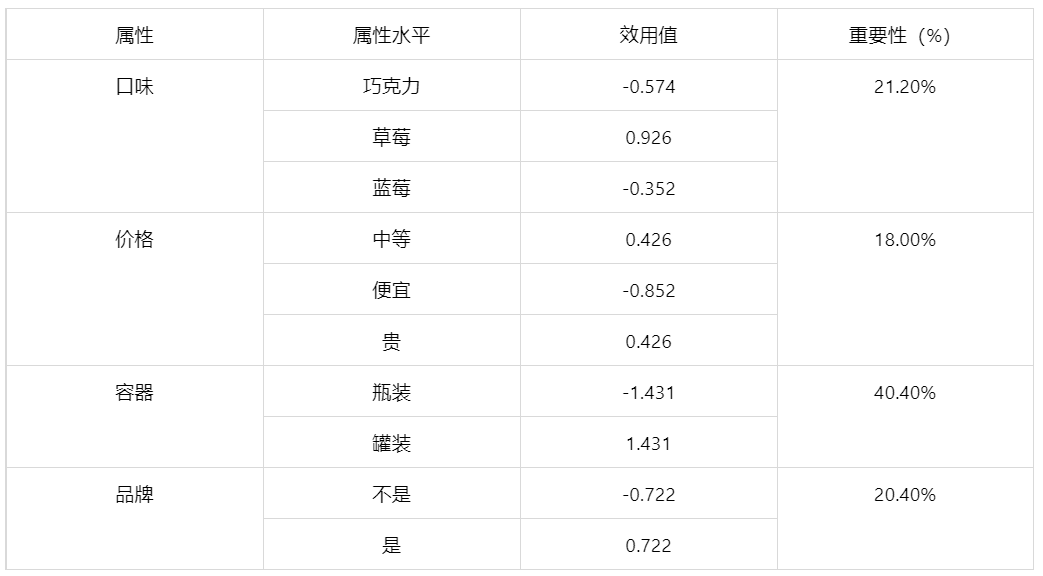
图表说明：上表格展示了各属性的效用值及重要性。
结果分析：在同一属性下的回归系数就表示了该属性水平的效用 (分值 )减去属性基础水平的效用(分值)，由此可以求效用值。并且由重要性公式计算得到，口味的重要性为 21.2%、价格的重要性为 18.0%、容器的重要性为 40.4%、品牌的重要性为 20.4%，其中最大重要性为 40.4%，最小重要性为 18.0%。
​

输出结果 3：属性相对重要性图

图表说明：上图展示了属性的相对重要性。


​

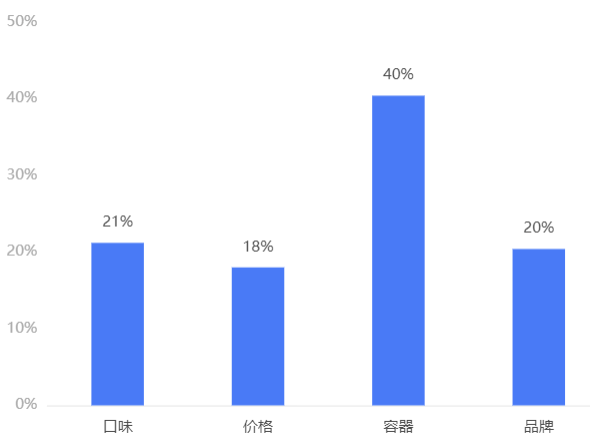
输出结果 4：预测最优的属性组合 ​

口味	价格	容器	品牌
草莓	中等	罐装	是

图表说明：上表展示了根据效用值求最优的属性组合。由表可知，口味为草莓、价格为中等、容器为罐装、品牌为是的属性组合是最优的。这样的话，就有利于商家根据该属性组合来对饮料进行生产决策。

# 7、注意事项

• 属性的个数及属性水平不宜过多，一般情况下，属性个数控制在 6 个以内，这是因为因变量是由受访者评价得分的，若属性水平过多，会导致受访者难以作出客观的判断。

# 8、模型理论

联合分析是通过假定产品具有某些特征，对现实产品进行模拟，然后让消费者根据自己的喜好对这些虚拟产品进行评价，并采用梳理统计的方法将属性水平效用进行分离，从而对每一属性及属性水平的重要程度作出量化评价的方法。
Spsspro 联合分析中，自变量要求是各属性的值；因变量是是通过消费者访问的形式进行的，一般可以对每一个模拟对象给予一个分值，或给予一个喜好顺序号。

$y=\sum _{j=1}^J\sum _{i=1}^I{v}_{ij}{x}_{ij}$

其中：y 为用户体验的总效用值；$v_{ij}$ 表 示第 j 个属性的第 i 个水平的效用值，当第 j 个属性的第 i 个水平出现时，$x_{ij}$=1，其他情况下 $x_{ij}$=0。
步骤1：对于效用值的求解，建立线性回归方程。

$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+...+{\beta }_k{x}_k+\epsilon$

其中$x_1...x_k$分别表示k个属性，利用哑元法对各个属性进行量化，建立线性方程，并应用最小二乘法求得回归系数bi。
步骤2：系数 (bi)就表示了该水平的效用 (分值 )减去基础水平的效用(分值)，由此我们可以列出公式求出$v_{ij}$。
步骤3：属性的相对重要度可进行计算

$R_j=\frac{max(v_{ij})-min(v_{ij})}{\sum _{j=1}^J[max(v_{ij})-min(v_{ij})]}\times 100\mathrm{\%}$

其中：$R_j$为第 j 个属性相对重要度；$max(v_{ij})$为第 j 个属性水平效用值的最大值；$min(v_{ij})$为第 j 个属性水平效用值的最小值 。 ​

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 叶小青. 联合分析在手机新产品开发上的应用研究[J]. 中南民族大学学报（自然科学版）,2011,30(3):111-115. DOI:10.3969/j.issn.1672-4321.2011.03.027.