选择题【多选&单选】

操作视频

# 选择题【多选&单选】

# 1、作用

多选-单选题分析是针对问卷调研设计的一种以多选题为分组项，分析单选题的分布比例情况的分析办法。多选题一般一个选项是单独的一个标题，比如 5 个选项就有 5 个标题，多选题分析就是用于分析调研用户对多选题各个题项的选择比例。单选题通常是例如性别、学历等定类变量。

# 2、输入输出描述

输入：多选题选项至少两项或以上的二分类定类变量，需要注意的是，这里的二分类只能是 0，1，并且 1 代表选中，单选题为一个或一个以上的定类变量。
输出：以多选题各个选项作为分组，对单选题的选型分布情况进行交叉列联分析。

# 3、案例示例

案例：比如 “您日常出行的交通工具是什么”这个多选题与“您的职业”这个单选题，分析日常出行的交通工具偏向用户的职业差异性。

# 4、案例数据

选择题【多选&单选】案例数据

多选题选项至少两项或以上的二分类定类变量（案例中变量为：自行车、摩托车、公交地铁、网约车），需要注意的是，这里的二分类只能是 0，1，并且 1 代表选中，单选题（案例中变量为：职业）为一个或一个以上的定类变量。

# 5、案例操作

Step1：新建分析；
Step2：上传文件；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

Step4：选择【选择题【多选&单选】；
Step5：查看对应的数据数据格式，【选择题【多选&单选】要求一项输入数据为放入二分类 [定类] 变量（变量数 ≥2），一项输入数据放入 [定类] 变量（变量数 ≥1）；
Step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：多重响应频率分析表
图表说明：上表为多重响应频率分析表，展示了选项的频率分布情况，包括个案数、响应率及普及率、显著性 P 值等。
结果分析：根据的多重响应频率分析表显示，分析项：自行车、摩托车、公交、地铁、网约车的卡方拟合优度检验的显著性 P 值为 0.62,P 值大于 0.05，α=0.05 时水平上不呈现显著性，接受原假设，意味着各项的选择比例比较均匀，没有显著性差异。

输出结果 2：响应率

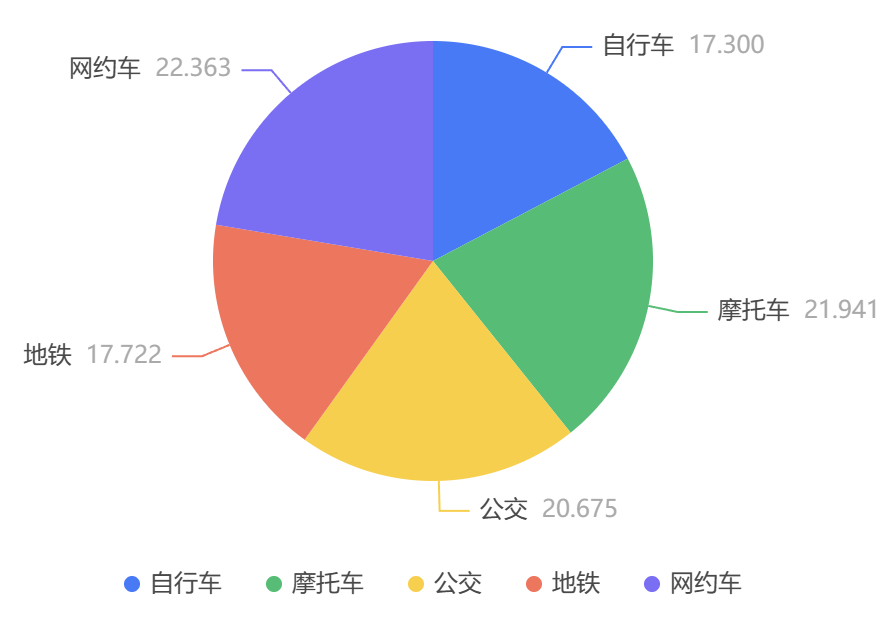
图表说明：上图以可视化的形式展示了多选题的各个问题选项响应率的频数分布情况。

输出结果 3：普及率

图表说明：上图以直方图的形式展示了各个问题选项普及率的分布情况。

输出结果 4：帕累托图

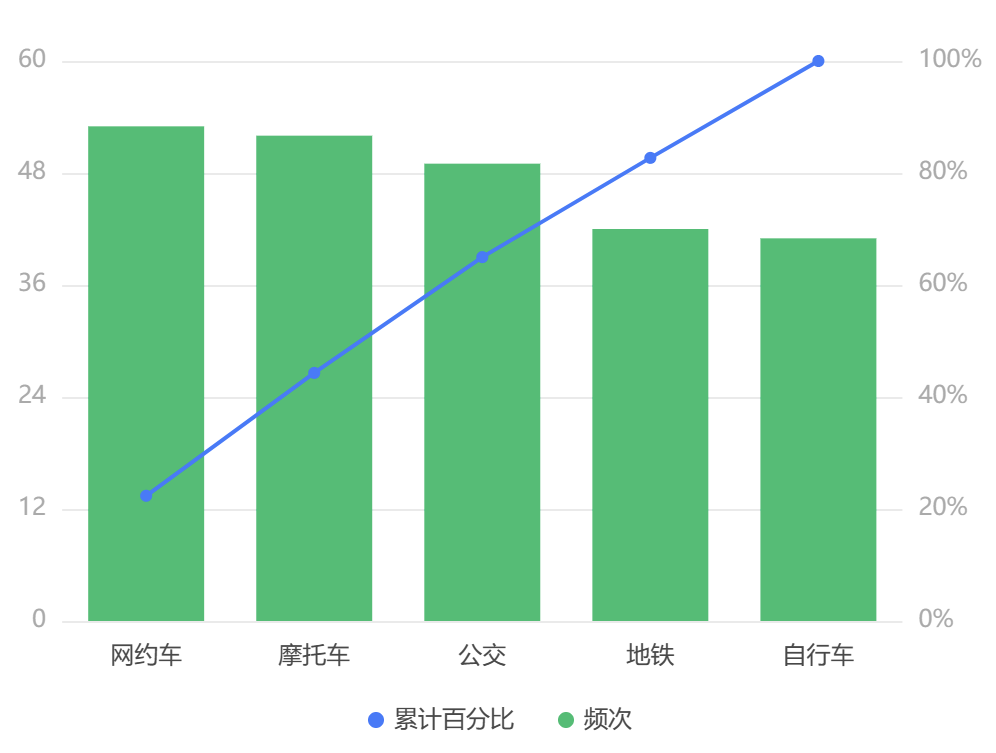
图表说明：帕累托图是“二八原则”的图形化体现，80%的问题是由 20%的原因所致。
结果分析：从上图可说明在六个选项中地铁和自行车是“微不足道项”，重要性较低。

输出结果 5：多重响应频率交叉分析表

图表说明：上表为多重响应频率交叉分析表，展示了选项的频率分布情况，包括个案数、响应率及普及率、显著性 P 值等。
结果分析：模型的多重响应分析交叉表显示，卡方检验的显著性 P 值为 0.455,P 值大于 0.05，在 α=0.05 时水平上不呈现显著性，接受原假设，说明不同的职业在自行车、摩托车、公交、地铁、网约车的选择上不具有显著性差异。

输出结果 6：交叉图

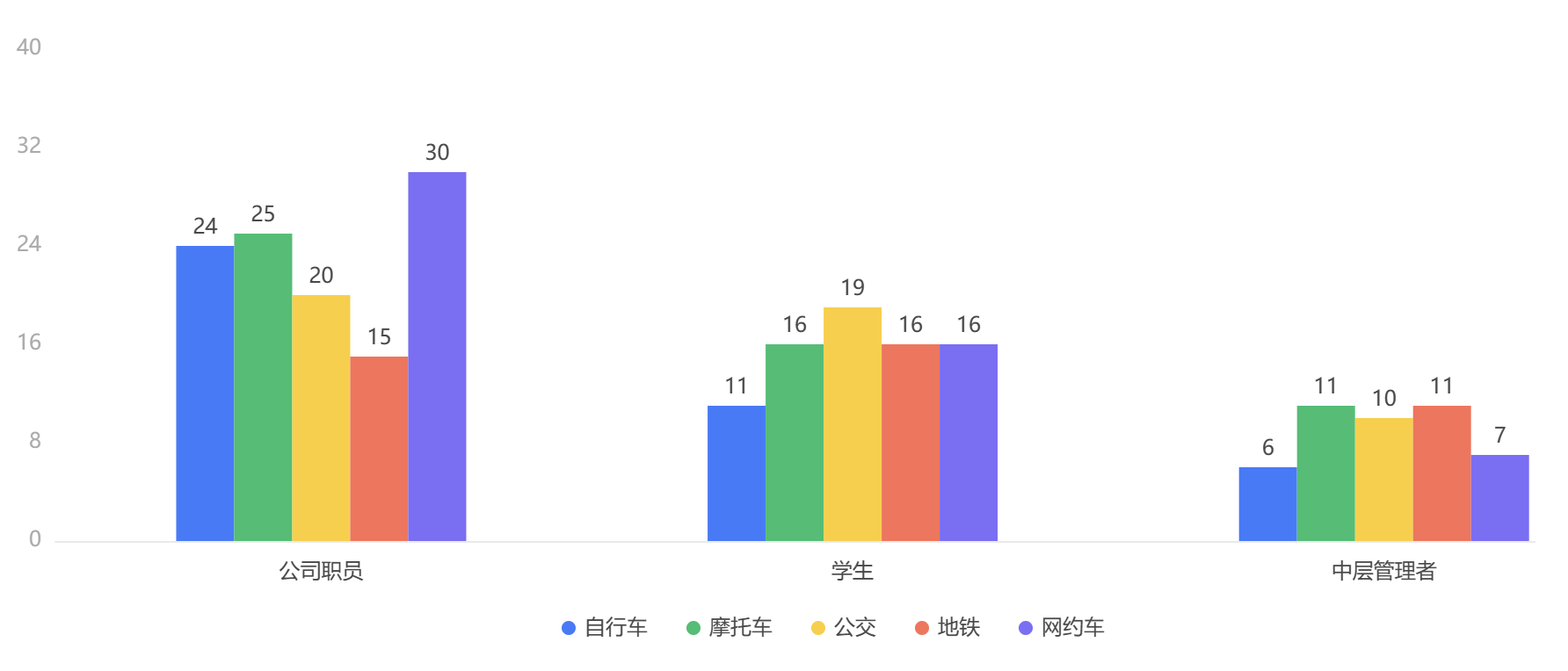
图表说明：上图展示了单选题选项与多选题选项的频数分布情况。

# 7、注意事项

多选题一般一个选项是单独的一个变量，比如 5 个选项就有 5 个变量，同时数据输入格式要求只能是 0，1，并且 1 代表选中；
多选题数据若不符合输入格式，请使用 SPSSPRO-数据处理-编码，进行处理；
从问卷网导入的数据 SPSSPRO 会自动处理，可以直接分析；
多选题会对响应率与普及率做卡方拟合优度，检验响应率与普及率是否呈现差异。

# 8、模型理论

响应率为多选题(X)各选项的全部选择项比例情况。例如一个多选题由 10 人回答，但是收获了 36 个选项，其中 A 选项有 8 个，A 的响应率=8/36。
普及率为有效样本下的各选项的选择比例，例如一个多选题由 10 人回答，其中 A 选项有 8 个，A 的普及率=8/10。
卡方拟合优度检验是用来检验观测数与依照某种假设或分布模型计算得到的理论数之间一致性的一种统计假设检验，以便判断该假设或模型是否与实际观测数相吻合。其步骤为：
1）将观测值分为 K 组。
2）计算 n 次观测值中每组的观测频数，记为 $O_{i}$ 。
3）根据变量的分布规律或概率运算法则，计算每组的理论频率为 $P_{i}$ 。
4）计算每组的理论频数 $T_{i}$ 。
5）检验 $O_{i}$ 与 $T_{i}$ 的差异显著性，判断两者之间的不符合度。
a、零假设： $H 0 ： O - T = 0$ ；备择假设： $H 1 ： O - T \neq 0$
b、检验统计量：这里要求 n 充分的大，当 n≥50 时（最好 ≥100），所定义的检验统计量近似服从卡方分布， $T_{i} = n P_{i}$ 不得小于 5，若小于 5，将尾区相邻的组合并，直到合并后的组的 $T_{i} \geq 5$ ，合并后再计算卡方值。

$$ \Large X_{df}^2=\sum_{i=1}^{k}\frac{(O_i-T_i)^2}{T_i} $$

c、建立拒绝域
d、作出统计学结论

帕累托图（Pareto Chart）又称排列图法、主次因素分析法，是一种条形图和折线图的组合，为品质管理上经常使用的一种图表方法。1930 年由约瑟夫·朱兰首次应用于品管当中。按照发生的频度排序，显示了多少结果是由每一个识别出来的原因产生。
帕累托图根据“关键的少数和次要的多数”的原理而制作，其结构为两个纵坐标和一个横坐标，合并长条图及折线图所构成。左侧纵坐标表示频率，右侧纵坐标则表示累计频率（以百分比表示），横坐标表示影响质量的各种因素之名称，按影响大小顺序排列，直方形高度表示相应的因素的影响程度（即出现频率为多少），上方之折线则表示累计频率线(又称帕累托图曲线)。

帕累托图

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 曾发恒.帕累托图法的应用[J].中国自行车,1987(02):31-32+30.
[3] 王重, 刘黎明. 拟合优度检验统计量的设定方法[J]. 统计与决策, 2010(5):154-156.

建议反馈