区分度分析

操作视频

# 区分度分析

# 1、作用

区分度分析是利用独立样本 T 检验对问卷数据收集时是否存在差异性进而研究区分度的一种方法。其原理为，对分析项求和【如品牌的潮流度打分，价格打分，舒适度打分】，然后将平均数据分成三部分按 37 分或者其他比例分别分为低分组，中分组和高分组，然后使用独立样本 t 检验去对比各分组之间是否有着明显的差异，如果具有明显的差异，则说明具有良好的区分性。

# 2、输入输出描述

输入：至少一项或以上的定量数据或者有序定类数据。
输出：该问卷数据是否能够很好地对调查结果的评分进行区分。

# 3、案例示例

案例：比如对某品牌的潮流度打分，价格打分，舒适度打分求平均，得到总评分。对总评分按照（27、46、27）比例进行分组，并看总评分各组之间是否有明显的差异。

# 4、案例数据

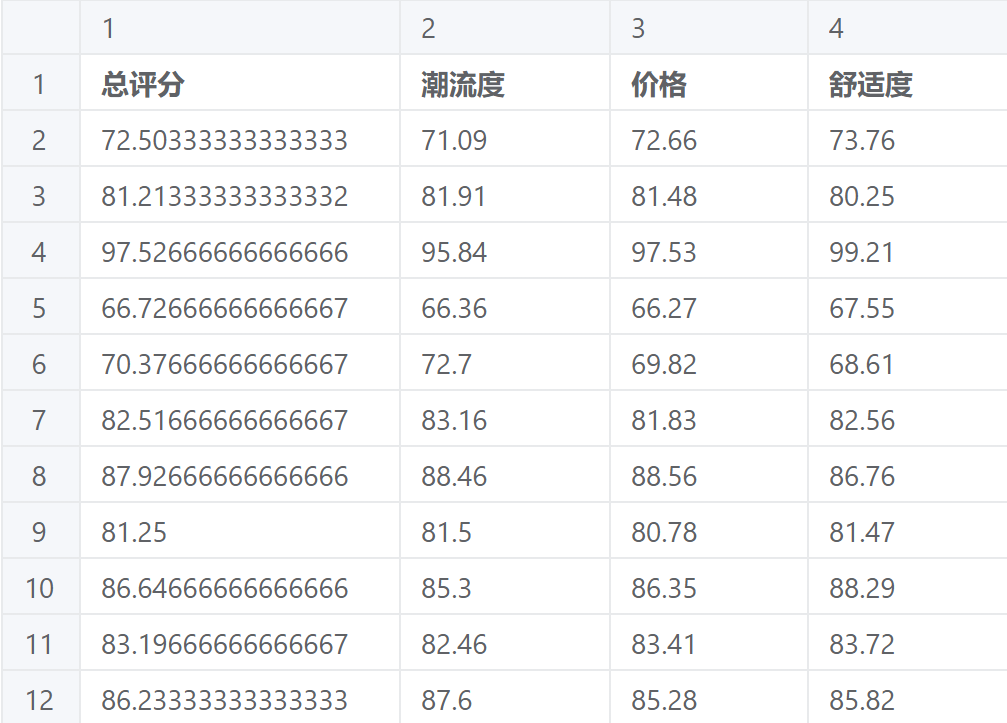
区分度分析案例数据

算法需要至少一项或以上的定量数据或者有序定类数据，案例数据使用的为一项定量数据（总评分列），有序定类数据指的是类似差、中、好这种带有顺序意义的离散数据。

# 5、案例操作

Step1：新建分析；
Step2：上传文件；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

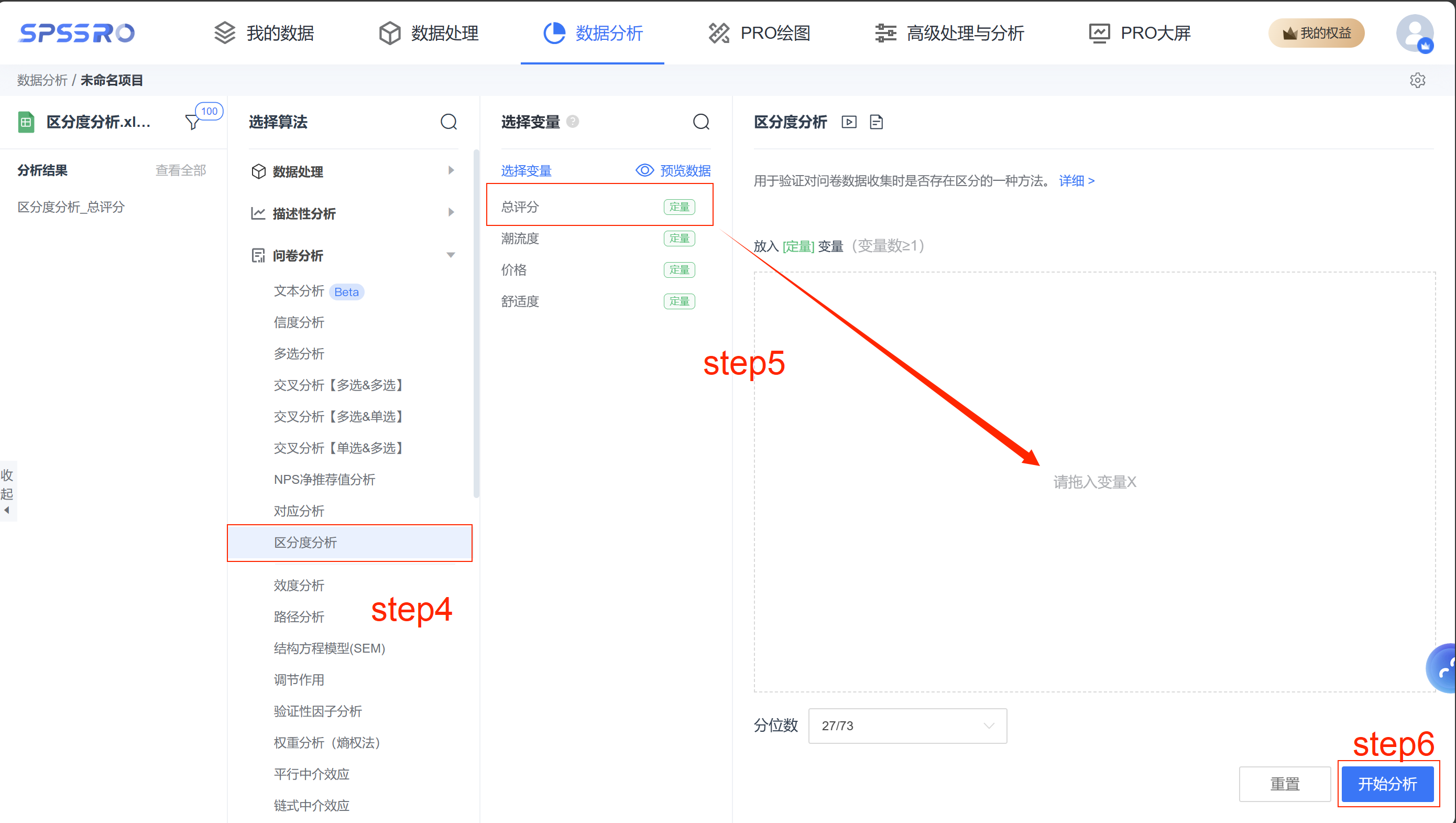
Step4：选择【区分度分析】；
Step5：查看对应的数据数据格式，【区分度分析】要求特征序列;
Step6：设置分位数，如“27/73”是指对数据进行分组（分成 0%-27%，27%-73%, 73%-100%);
Step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：区分度分析结果 

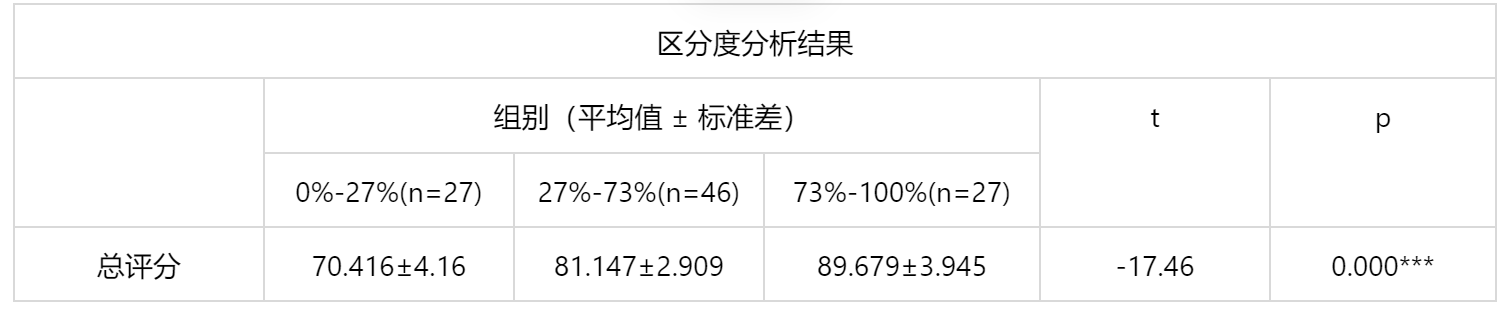
图表说明：上表展示了区分度分析结果，包括均值±标准差的结果、T检验结果、显著性P值等。

分析每个分析项的P值是否显著(P<0.05)。
若呈显著性，根据均值与检验值进行差异分析，描述差异大小，如果有差异则说明量表项设计合适，反之则说明量表项无法区分出信息，设计不合理应该进行删除处理。

结果分析：对于变量总评分，显著性 p 值为 0，水平上呈现显著性，拒绝原假设，说明量表项设计区分度高，设计较为合理。

输出结果 2：各分组均值对比图

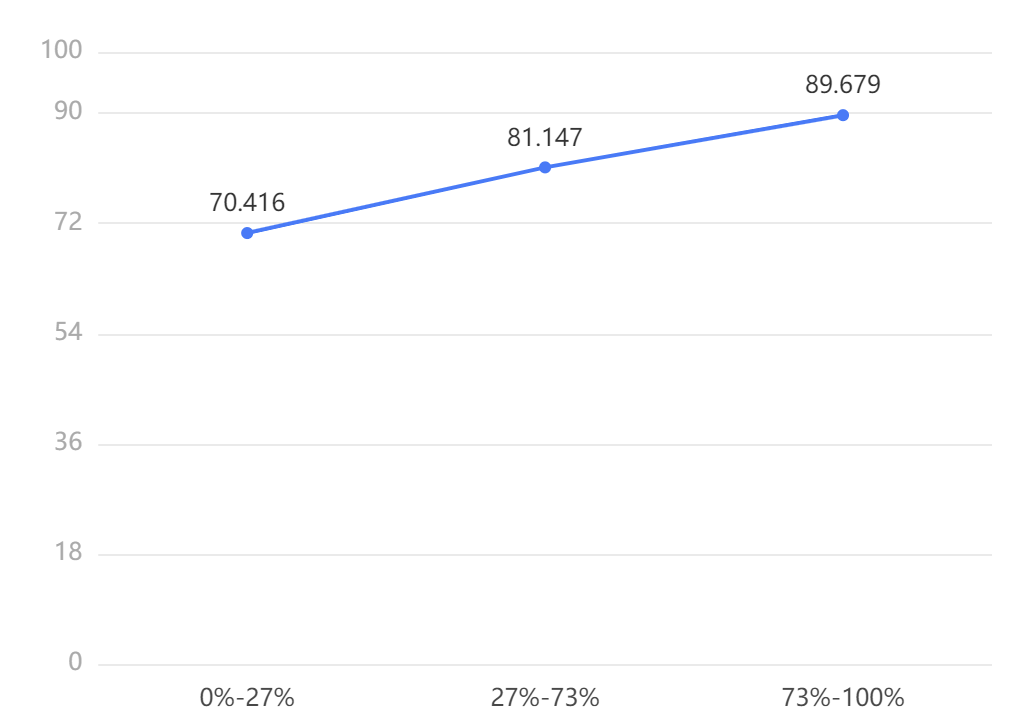
图表说明：上表展示了数据低中高分组的均值的结果，通过比较均值，可以挖掘其差异关系。

# 7、注意事项

一般情况下，如果数据组别的均值不能呈现出显著性差异，或者差异程度过小，可认为该项没有区分意义，予以删除处理。

# 8、模型理论

区分度的计算，取总分上位（得分高的群）27%和下位（得分低的群）27%两个群体(舍弃中间群体 46%)，而后对得分高的群和得分低的群进行独立样本 T 检验。
T 检验是比较两组数据之间的差异，有无统计学意义；T 检验的前提是，两组数据来自正态分布的群体，数据的方差齐，满足独立性。
独立样本 T 检验（各实验处理组之间毫无相关存在，即为独立样本），该检验用于检验两组非相关样本被试所获得的数据的差异性。
独立样本 T 检验统计量为：

t = \frac{\bar{X_{1}} - \bar{X_{2}}}{\sqrt{\frac{(n_{1} - 1) S_{1}^{2} + (n_{2} - 1) S_{2}^{2}}{n_{1} + n_{2} - 2} (\frac{1}{n_{1}} + \frac{1}{n_{2}})}}

$S_{1}^{2}$ 和 $S_{2}^{2}$ 为两样本方差； $n_{1}$ 和 $n_{2}$ 为两样本容量。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] Fisher Box, Joan. Guinness, Gosset, Fisher, and Small Samples. Statistical Science. 1987, 2 (1): 45–52.

建议反馈