# 权重分析(熵权法)

# 1、作用

权重分析是通过熵权法对问卷调查的指标的重要性进行权重输出，根据信息熵的定义，对于某项指标，可以用熵值来判断某个指标的离散程度，其信息熵值越小，指标的离散程度越大， 该指标对综合评价的影响（即权重）就越大，如果某项指标的值全部相等，则该指标在综合评价中不起作用。因此，可利用信息熵这个工具，计算出各个指标的权重，为多指标综合评价提供依据。

# 2、输入输出描述

输入：至少两项或以上的定量变量（正向指标与负向指标），一般要求数据为量表量数据。
输出：输入定量变量对应的权重值。

# 3、案例示例

案例：数据是 100 个客户的各方面（能力，品格，担保，资本，环境）评分，利用熵权法来计算各个变量（能力，品格，担保，资本，环境）的重要性，即所占的权重。

# 4、案例数据

权重分析（熵权法）案例数据

模型要求为至少两项或以上的定量变量（正向指标与负向指标），一般要求数据为量表量数据，可以均为正向指标或负向指标。其中能力，品格，担保，资本，环境均为正向指标。

# 5、案例操作

Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

Step4：选择【权重分析(熵权法）】；
Step5：查看对应的数据数据格式，【权重分析(熵权法）】要求特征序列为类变量，且至少有两项；
Step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果1​：权重分析计算结果

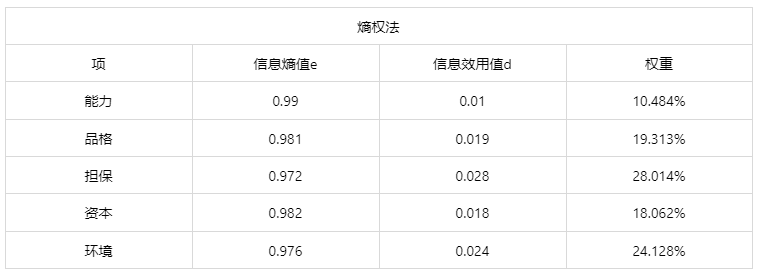
图表说明：上表展示了熵权法的权重计算结果，根据结果对各个指标的权重进行分析。
结果分析：熵权法的权重计算结果显示能力的权重为10.484%、品格的权重为19.313%、担保的权重为28.014%、资本的权重为18.062%、环境的权重为24.128%,其中指标权重最大值为担保(28.014%),最小值为指标能力(10.484%)
​

输出结果 2：指标重要度直方图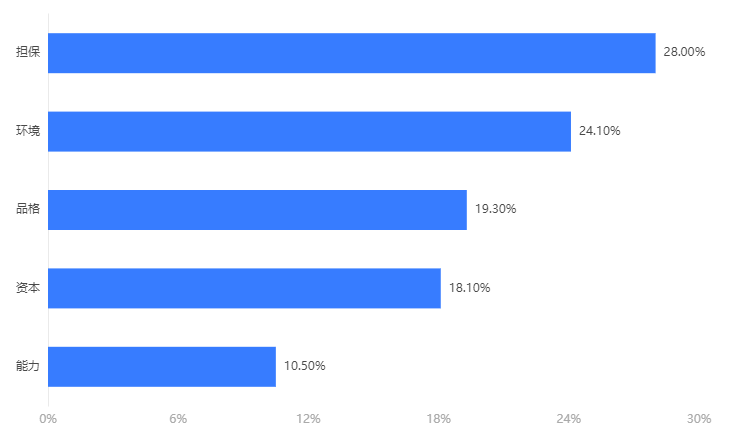

图表说明：可选择直方图、折线图、条形图、饼图四种方式对权值比重进行可视化。上图以直方图为例。

# 7、注意事项

• SPSSPRO 默认会对指标进行正、负向指标处理，通过处理，数据就无需再进一行标准化；
• 熵权法得到权重值后，此时数据与对应的权重相乘，并且进行累加，最终得到一列数据即为‘综合得分’；

# 8、模型理论

熵是信息论中的概念，是对不确定性的一种度量。信息量越大，不确定性越大，熵就越大；信息量越小，不确定性越小，熵也越小。根据信息熵的定义，对于某项指标可用熵值来判断某个指标的离散程度，信息熵越小表示指标的取值分布越集中和稳定，相对而言，其对应的权重在综合评价中应该更大；反之，信息熵越大则对应的权重应该较小。
其步骤为：
（1）对各个因素按照每个选项的数量进行归一化处理
由于平台存在“正向指标”、“负向指标”，将分别对这两类数据做预处理 。 这里对最小值减去0.0001，对最大值加上0.0001是为了兼容一整列都为相同的值的情况，对整体结果影响不大，可忽略不计

$X_{min}=min(X_{1j},X_{2j},...,X_{nj})-0.0001$

$X_{max}=max(X_{1j},X_{2j},...,X_{nj})+0.0001$

对于正向指标：

$z_{ij}=\frac{X_{ij}-X_{min}}{X_{max}-X_{min}}$

对于负向指标：

$z_{ij}=\frac{X_{max}-X_{ij}}{X_{max}-X_{min}}$

​ （2）计算第J项指标的熵值：

$e_j=-k\sum _{i=1}^n{p}_{ij}ln(p_{ij}),j=1,...,m$

（3）计算信息熵冗余度（差异）：

$d_j=1-e_j,j=1,...,m$

（4）计算各项指标的权重：

$w_j=\frac{d_j}{\sum _{j=1}^m{d}_j},j=1,...,m$

（5）计算各样本的综合得分：

$s_i=\sum _{j=1}^m{w}_j{x}_{ij},i=1,...,n$

其中，$X_{ij}$为归一化后的数据。根据每个影响因素的得分，即可得到所有因素的重要性排序。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 甘浪雄,张怀志,卢天赋,等. 基于熵权法的水上交通安全因素[J]. 中国航海,2021,44(2):53-58.