平行中介效应

# 平行中介效应

# 1、作用

中介效应分析是用来考察研究X影响Y时，是否会存在中介变量(以符号M表示)起桥梁作用的一套统计方法。帮助研究者处理出现多重测量时的中介作用、中介性的调节作用、调节性的中介作用以及中介作用这一主题下的其他议题。

# 2、输入输出描述

输入：一个定量变量作为因变量，一个以上的定量变量作为自变量，一个以上的定量变量作为中介变量，控制变量为定量变量（可不选）。
输出：在研究X与Y之间的影响时，中介变量M是否能对X→Y起影响作用。

# 3、案例示例

案例：当考虑房龄对房价的影响时，探究是否会存在中介变量影响房龄->房价这个流程。

# 4、案例数据

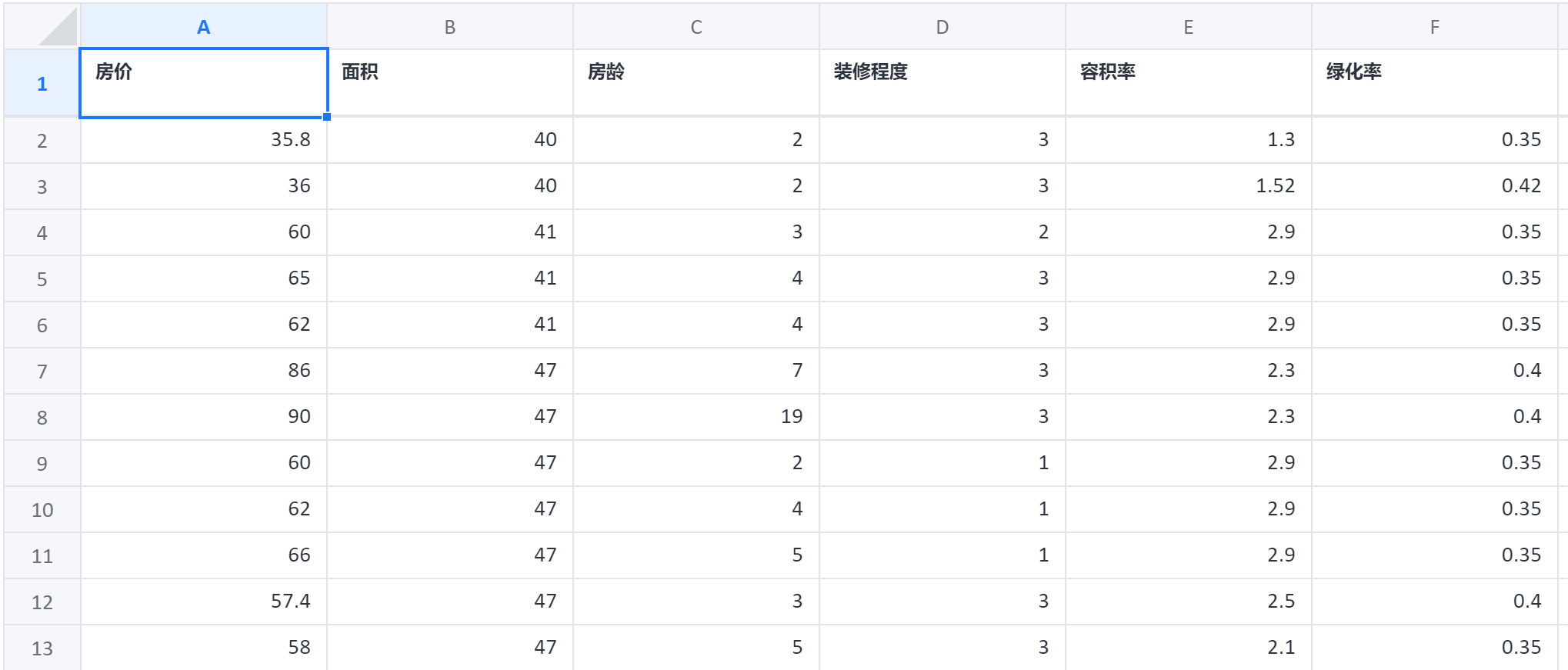
案例数据

模型要求一个定量变量作为因变量（房价），一个以上的定量变量作为自变量（房龄），一个以上的定量变量作为中介变量（容积率和面积），控制变量为定量变量（可不选）。

# 5、案例操作

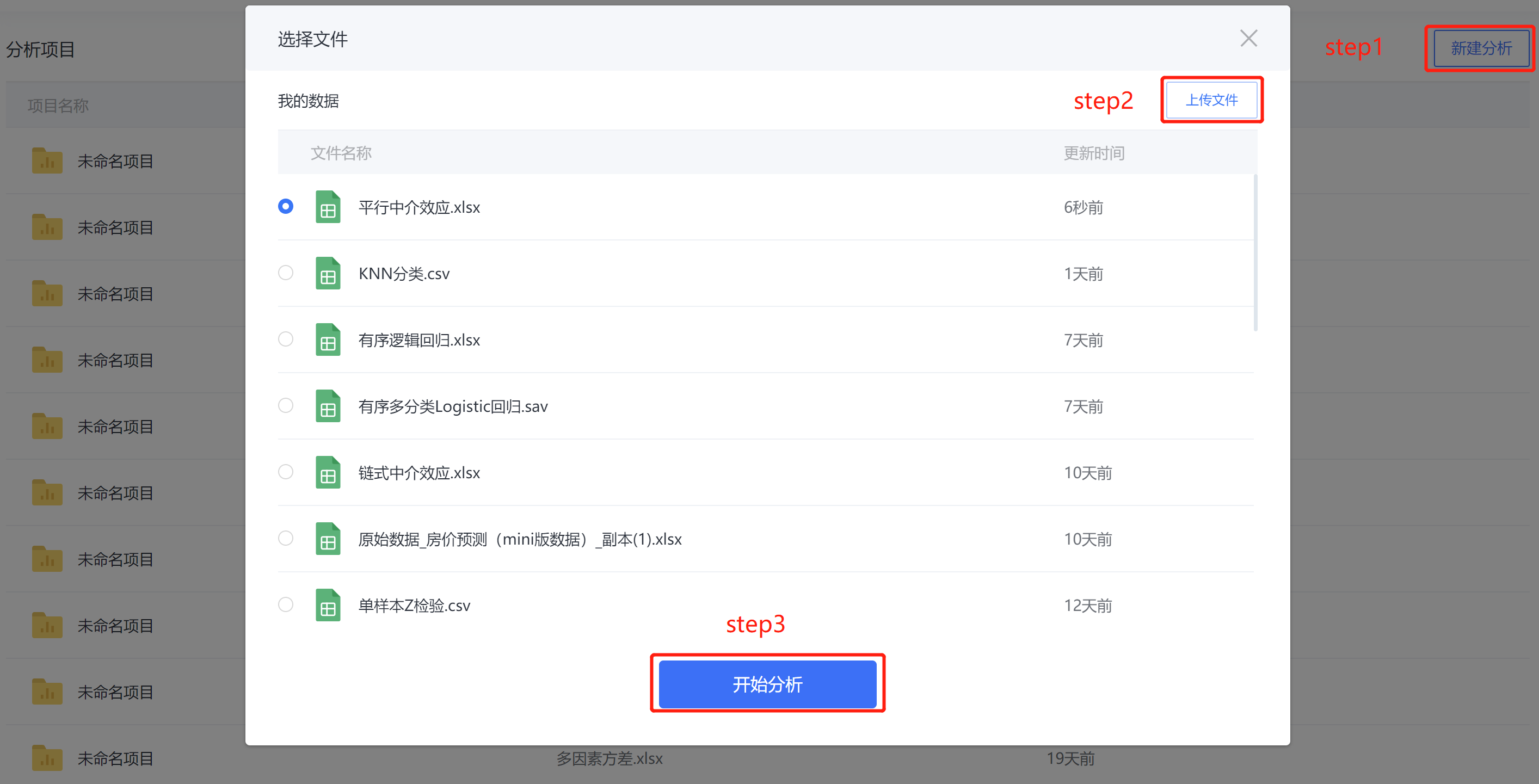
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

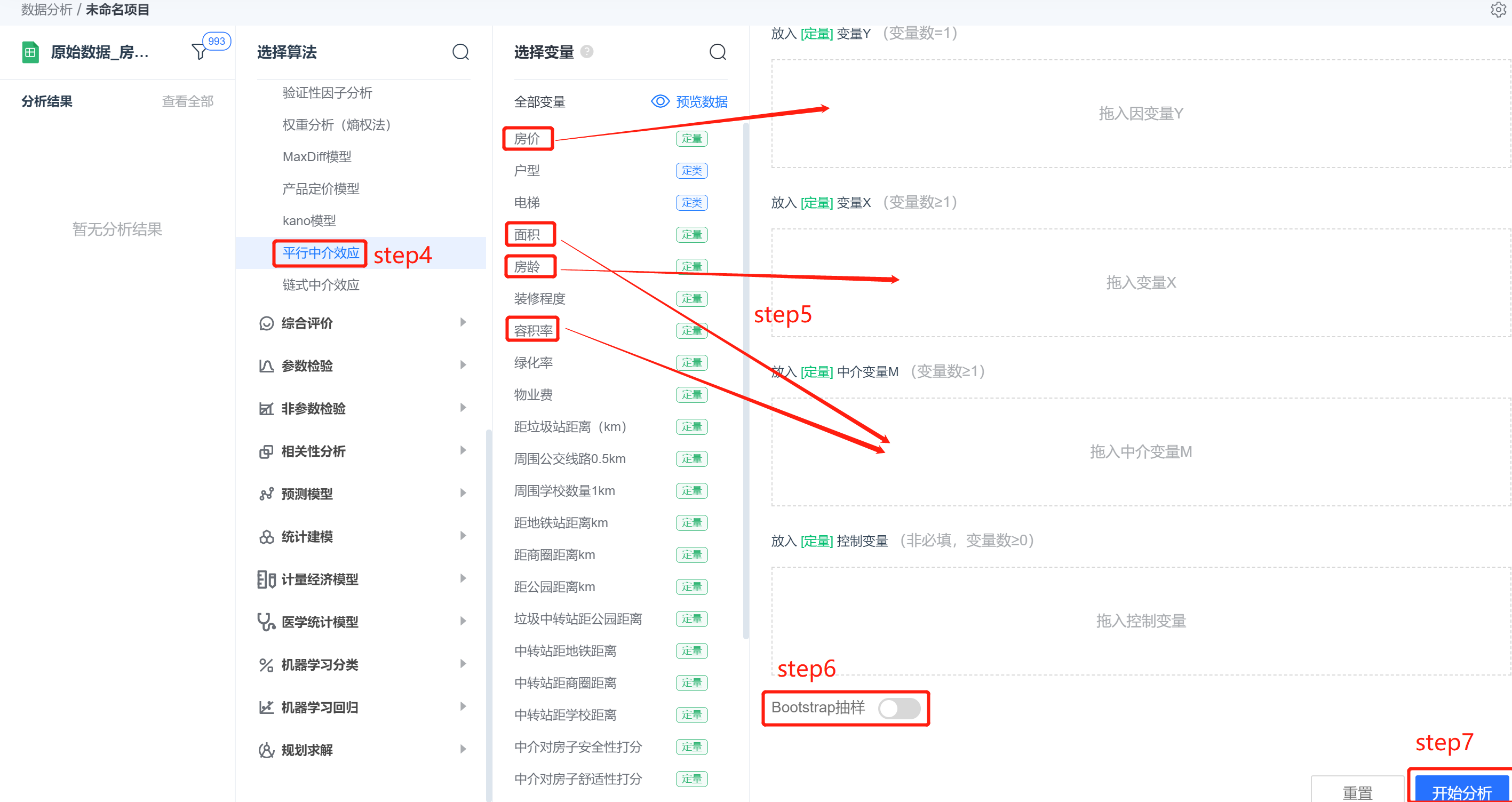
Step4：选择【平行中介效应】；
Step5：查看对应的数据数据格式，【平行中介效应】要求特征序列；
Step6：设置是否Bootstrap抽样；
Step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果1：中介效应回归模型系数表

	房价	面积	容积率	房价
常数	116.856	77.159	2.543	-20.338
房龄	0.037	0.243	-0.031	0.077
面积				1.383
容积率				11.994
样本量	779	779	779	779
R²	0	0.005	0.052	0.506
调整R²	-0.001	0.003	0.05	0.503
F值	F(1，777)=0.025，p=0.875	F(1，777)=4.078，p=0.044**	F(1，777)=43.037，p=0.000***	F(3，775)=264.331，p=0.000***

注：***、**、*分别代表1%、5%、10%的显著性水平
图表说明：上表展示了中介效应三类回归模型的参数结果，包括非标准化系数、标准化系数、𝑡值、显著性𝑝值、拟合𝑅²，F检验等。
● 模型1： $Y = C_{1} X_{1} + . . . . . . + C_{n} X_{n} + e_{1}$ ，即自变量X与因变量Y进行回归模型构建；
● 模型2： $M 1 (1 M) = A_{1} X_{1} + . . . . . . + A_{1} X_{n} + e_{2}$ ，即自变量X与中介变量M进行回归模型构建(如果多个中介变量则多个模型)；
● 模型3： $Y = C_{1}^{'} X_{1} + . . . . . . + C_{n}^{'} X_{n} + B_{1}^{'} X_{1} + . . . . . . + B_{n}^{'} X_{n} + e_{3}$ ，即自变量X和中介变量M一起与因变量Y进行回归模型构建。
PS：若中介变量大于等于2个，采用简化的输出格式，若超过层次10个，预览前10个，全部数据请点击右上角进行下载。

输出结果2：中介效应检验汇总结果表

c 总效应	a	b	a*b中介效应值	a*b (Boot SE)	a*b (z值)	a*b (p值)	a*b (95%BootCI)	c' 直接效应	检验结论
0.037	0.243	1.383	0.337	0.2	1.682	0.093*	0.711 - -0.052	0.077	完全中介
0.037	-0.031	11.994	-0.376	0.075	-5.013	0.000***	-0.238 - -0.533	0.077	完全中介

图表说明：上表展示了中介效应检验结果，包括效应判断参数与效应占比等。
● 判断中介效应，判断要点如下：如果a和b显著，且c'不显著，则为完全中介如果a和b显著，且c'显著，且a*b与c'同号，则为部分中介作用，若为异号，则为遮掩作用如果a和b至少一个不显著，且a*b的95% BootCI包括数字0（不显著），则中介作用不显著；若不包括数字0，且c'不显著，则为完全中介；若不包括数字0（显著），且c'显著，且a*b与c'同号，则为部分中介作用；若不包括数字0（显著），且c'显著，且a*b与c'异号，则为遮掩作用；其中：c表示模型1中X对Y时的回归系数（模型中无中介变量M时），即总效应； a表示模型2中X对M时的回归系数，b表示模型3中M对Y时的回归系数，a*b为a与b的乘积即中介效应；95% BootCI表示Bootstrap抽样计算得到的95%置信区间，如果区间不包括0则说明显著； c'表示模型3中X对Y时的回归系数（模型中有中介变量M时），即直接效应；
● 完成中介作用检验后，还可进一步分析效应量（效应占比）如果是完全中介，则效应占比为100%；如果是部分中介，则效应占比计算公式为：a*b/c；如果是遮掩效应，则效应量为中介效应与直接效应的比值，计算公式为： $| a * b / c |$ ；如果是中介作用不显著，则效应占比为0%。

输出结果3：中介效应路径图

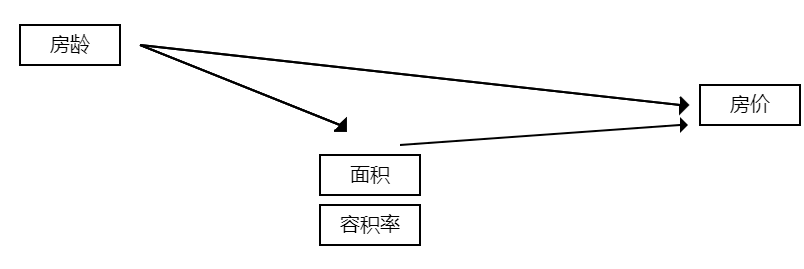
图表说明：上图以路径图形式展示了本次模型结果，用于可视化分析X对于Y的中介影响关系情况。

# 7、注意事项

逐步检验回归系数方法简单易懂，是检验中介效应最常用的方法；
逐步检验的检验力在各种方法中是最低的。就是说，当中介效应较弱的时候，逐步检验回归系数的方法很难检验出中介效应显著，但反过来理解，温忠麟等 (2014) 提出如果研究者用依次检验已经得到显著的结果, 检验力低的问题就不再是问题；

# 8、模型理论

# 1.中介效应介绍

当考虑自变量X对因变量Y的影响时，如果X通过影响变量M来影响Y,则称M为中介变量。X通过中介变量M对Y产生的影响就是中介效应。因此，在从自变量X到因变量Y的因果路径中，中介变量处于中间位置。也可以说，中介变量传递了自变量对因变量的效应。并且，中介关系也暗示了变量在时间上的先后顺序，即X的发生先于M，而M的发生又先于Y。
例如，父亲的社会经济地位通过影响儿子的受教育程度，从而影响儿子的社会经济地位。在这个例子中，儿子的受教育程度就是一个中介变量。下图为该例对应的中介模型。

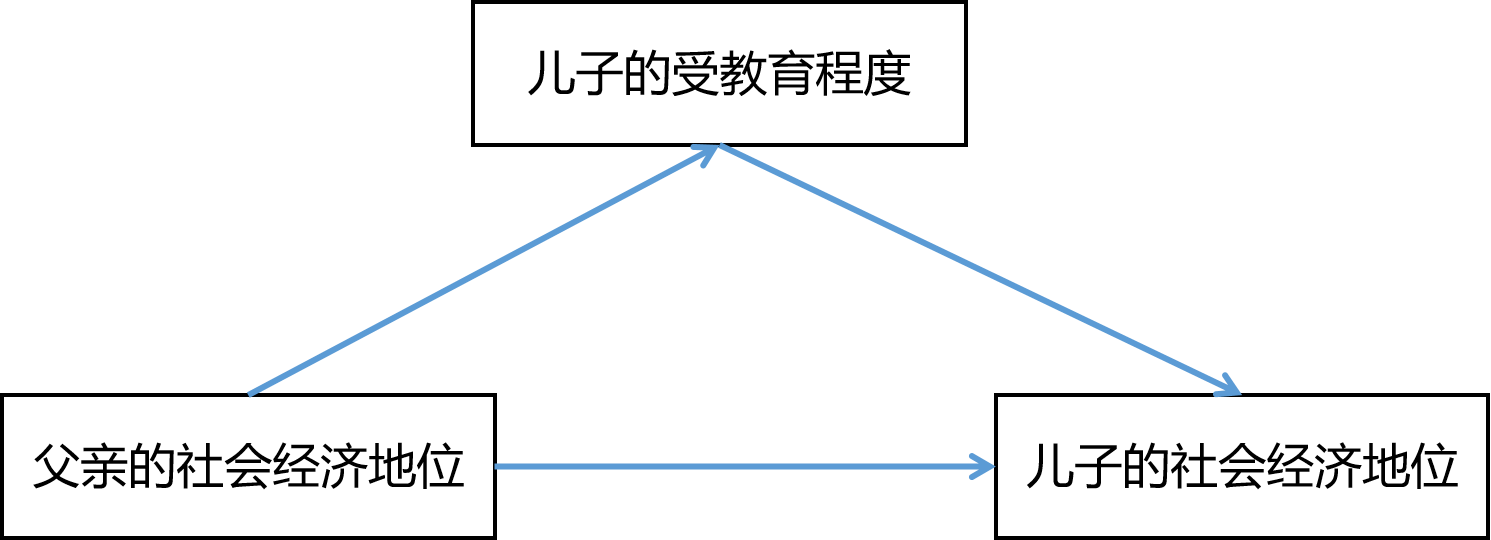
中介模型

# 2.平行中介模型

平行中介是指几个中介变量如M1,M2都在自变量X对因变量Y的影响中起着同等的中介作用; 平行中介模型是指中介变量之间互不影响的模型。

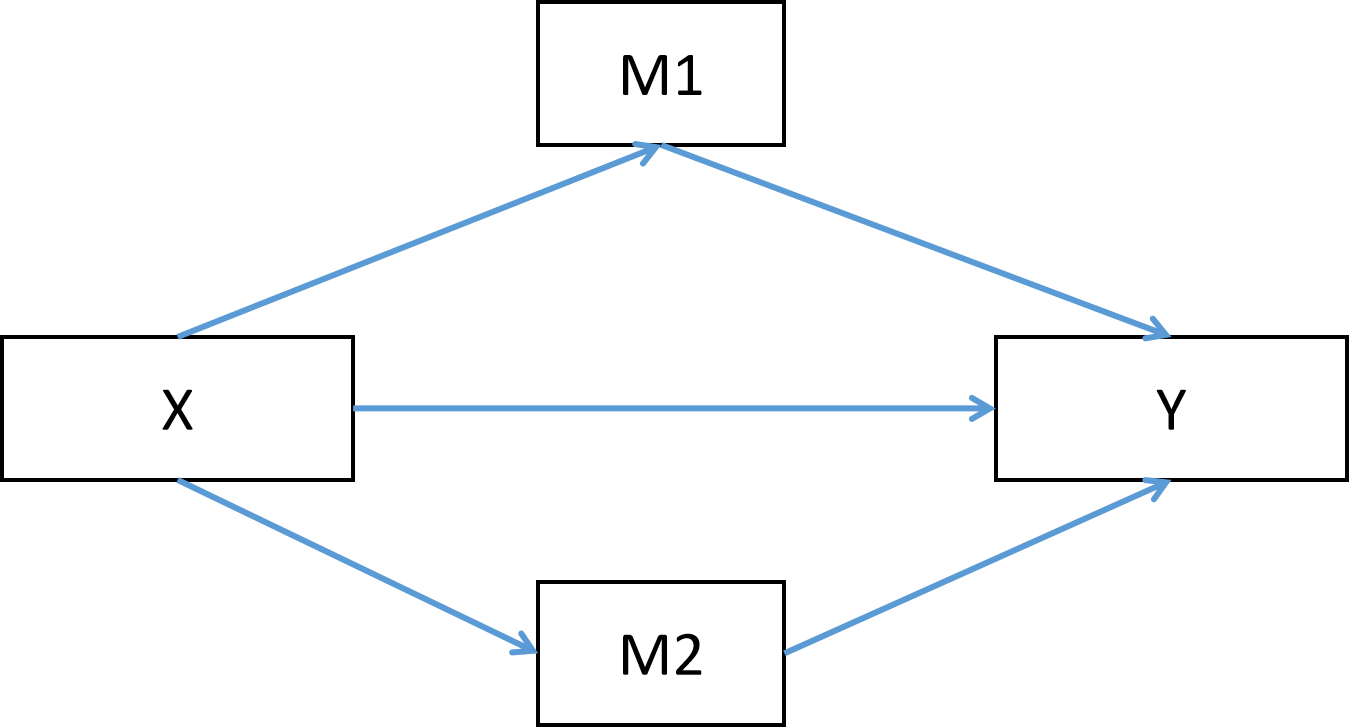
平行中介模型

# 3.中介关系假设

实际中变量之间可能存在的关系很多，研究者是无法根据数据完全将中介效应和其他的第三变量效应区分开。如何确立中介变量或如何建立中介关系的假设，理论信息、前人研究结论、预研究等是重要的假设依据，需要研究者依靠这些信息做出变量间作用关系的假设，再使用数据对这些假设进行验证。

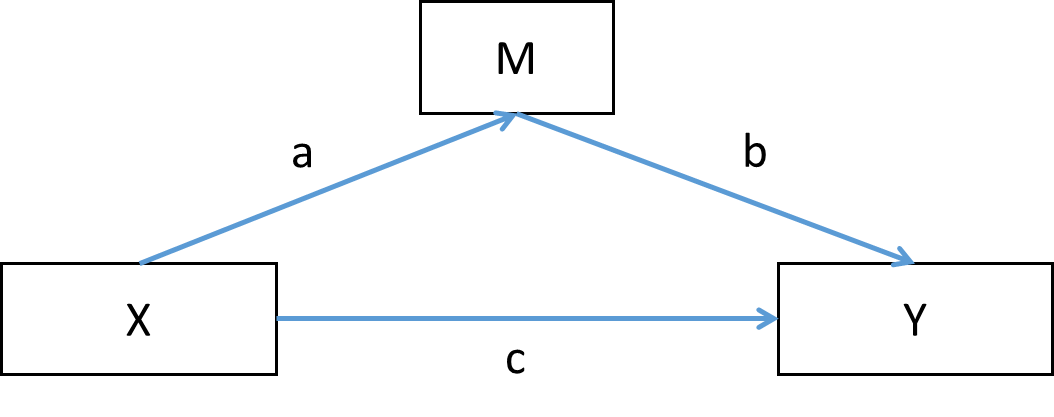
中介变量、自变量、因变量的联系
X是自变量，Y是因变量，M是中介变量。c是X对Y的总效应，a、b是经过中介变量M的中介效应，c'是直接效应。根据Baron和Kenny等人的研究，符合以下标准的变量可以判定为中介变量：
①X 与 M 显著相关，
②M 与 Y 显著相关。该标准被业内广泛接受并运用。
接下来Baron＆Kenny推荐sobel的Z检验对M进行假设检验:

Z = \frac{a \times b}{\sqrt{b^{2} s_{a}^{2} + a^{2} s_{b}^{2}}}

此处a,b为路径a、b的估计:

S_{a b} = \sqrt{a^{2} s_{b}^{2} + b^{2} s_{a}^{2}}

S_{a b}

是ab的标准误,

S_{a}

与

S_{b}

分别为a,b的标准误。

# 4.对中介变量进行假设检验

1）Baron和Kenny的逐步法
步骤一:根据Baron＆Kenny等人提出的回归模型，对上述的图中的路径a,b,c分别进行线性回归得出下式：
模型1：自变量X和因变量（Y）的回归分析
模型2：自变量X和中介变量（M）的回归分析
模型3：自变量X，中介变量(M)和因变量（Y）的回归分析

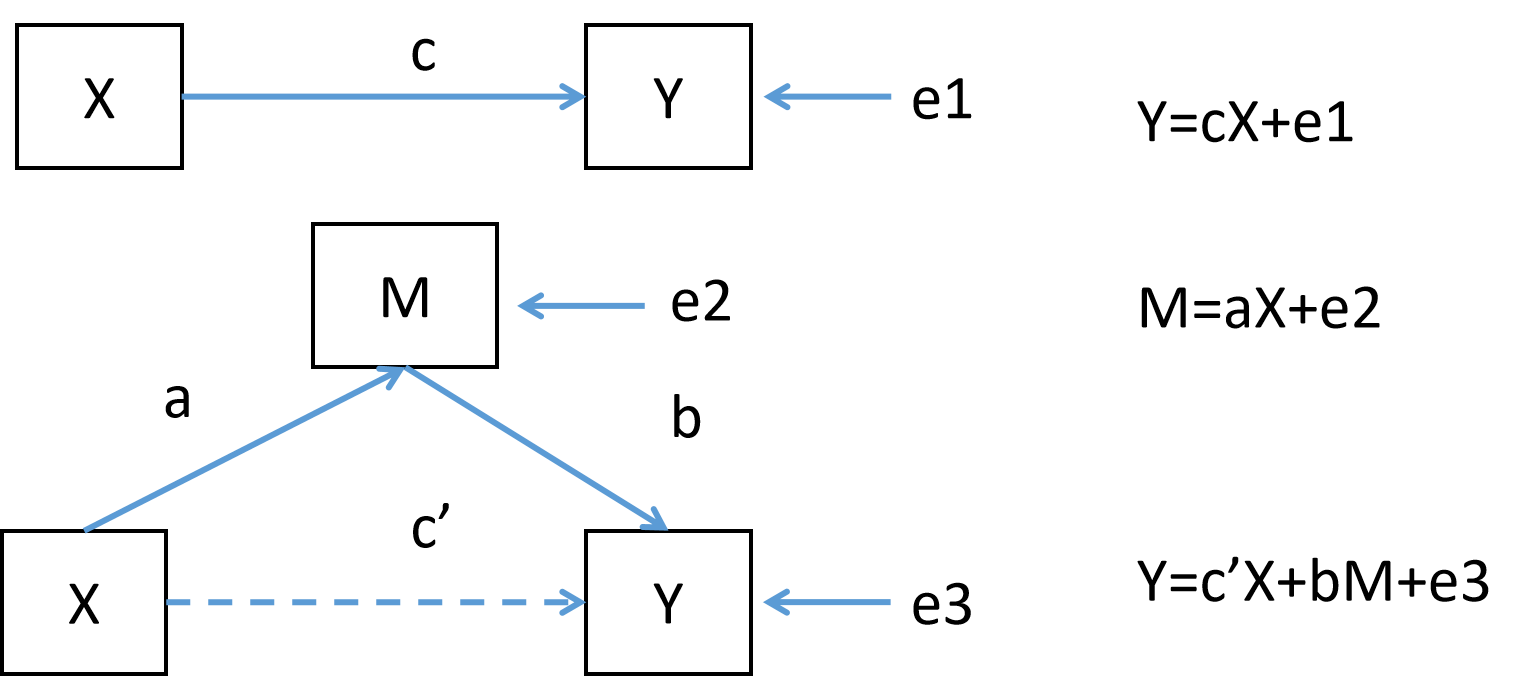
中介变量检验的线性回归模型
模型中a代表X对M的回归系数，b代表M对Y的回归系数，c代表X对Y的回归系数，c'代表X对Y的回归系数。

步骤二:
检验中介效应是否存在，其实就是检验X到M，M到Y的路径是否同时具有显著性意义。

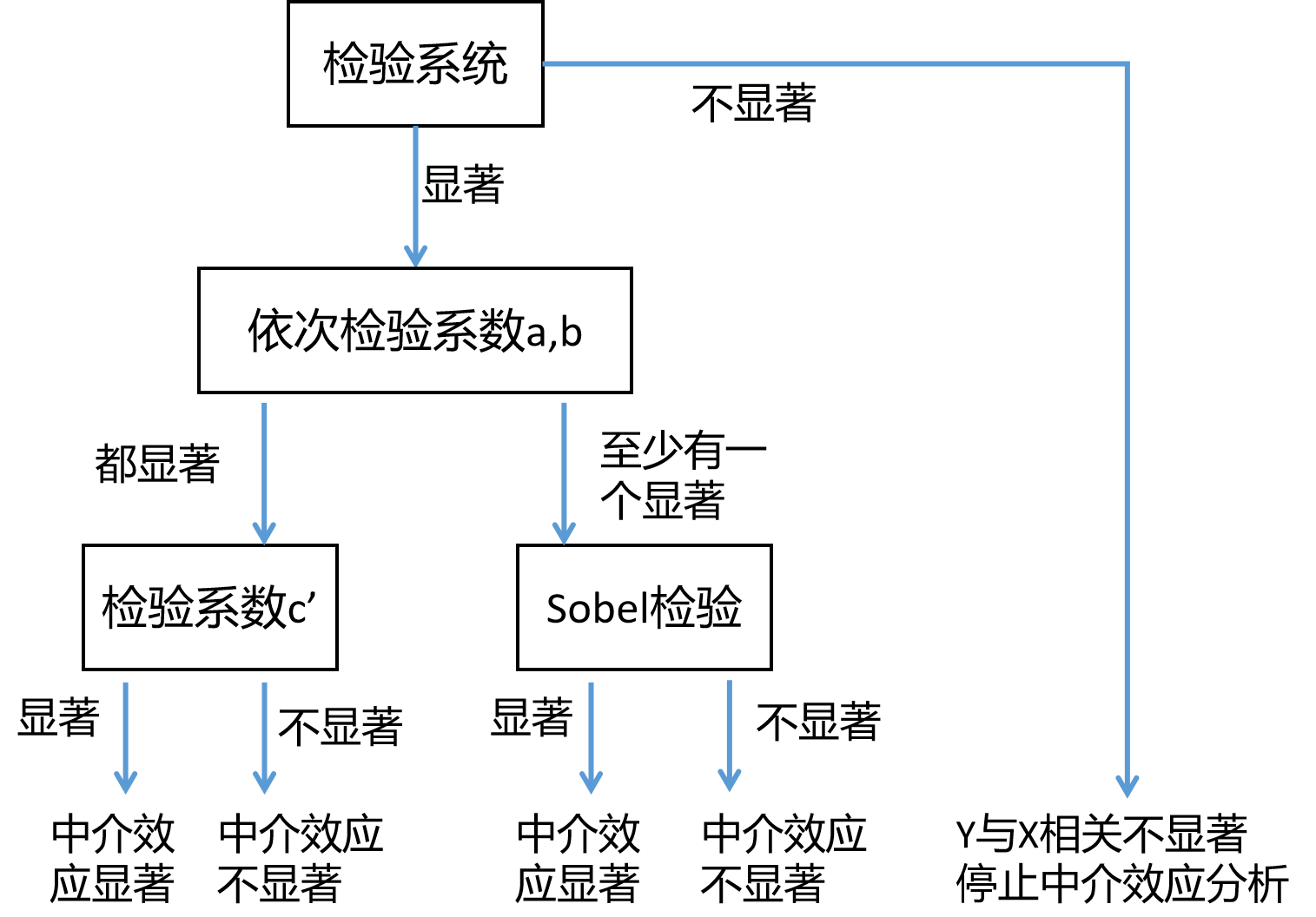
中介变量检验的Baron和Kenny的逐步法

2）bootstrap抽样法
bootstrap抽样法是目前普遍认为比较好的直接对a、b的乘积进行检验的方法：

Hayes和Preacher(2014)建议使用Bootstrap法进行相对中介效应的显著性判断，判断方法是求出的Bootstrap置信区间，如果置信区间不包含0，就表示相对中介效应显著。需要说明的是，类别自变量的水平数越多，需要检验的相对中介效应、直接效应和总效应就越多，这可能会导致检验的第一类错误率增大，Hayes和Preacher建议增加Bootstrap置信区间的置信度（用1–α/(k-1)代替通常的1–α）来控制检验的第一类错误率。
步骤①：对路径a、b的乘积进行检验，检验中介变量M是否存在中介效应；
步骤②：对总效应c′进行检验，检验自变量X是否直接对因变量Y有影响；
若步骤①和步骤②的结果都显著时，则继续进行步骤③；
步骤③：对路径a、b和总效应c′的乘积进行检验，确认中介变量M产生效应的作用方向。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 卢谢峰韩立敏《中介变量、调节变量与协变量——概念、统计检验及其比较》心理科学PsychologicalScience2007,30(4):934-936
[3] 甘怡群《中介效应研究的新趋势——研究设计和数据统计方法》中国心理卫生杂志，2014，28(8):584－585.
[4] 温忠麟,叶宝娟.中介效应分析:方法和模型发展[J].心理科学进展,2014,22(05):731-745.

建议反馈