对应分析

操作视频

# 对应分析

# 1、作用

对应分析（Correspondence analysis），又称为 R-Q 型因子分析，适用于有多个类别的分类变量，可以揭示同一个变量各个类别之间的差异，以及不同变量各个类别之间的对应关系，与卡方检验不同的是，对应分析不单单展示了不同分组的差异性，也能通过 2 维、3 维的方式构造散点图展示其在空间的关系,使联系密切的类别点较集中，联系疏远的类别点较分散。

# 2、输入输出描述

输入：至少两项或以上的定类变量。
输出：两个定类变量里面不同分组的空间关系与差异性。

# 3、案例示例

案例：检验不同收入的消费者对品牌的选择的距离。

# 4、案例数据

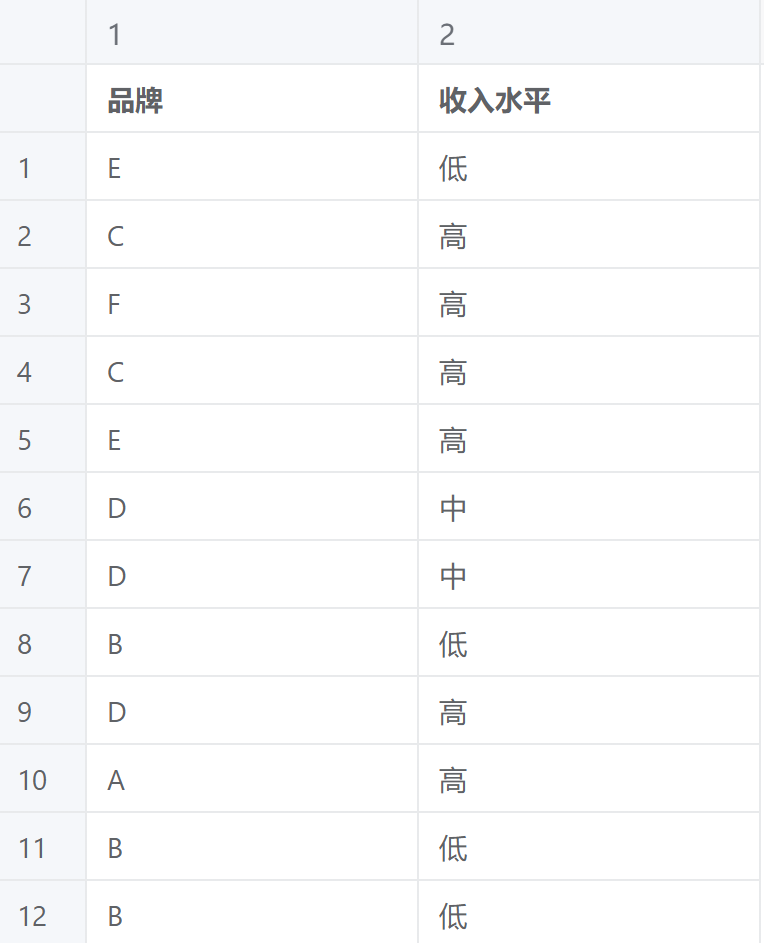
对应分析案例数据

算法至少两项或以上的定类变量，案例数据为品牌和收入水平两个定类变量，定类变量即为离散变量。

# 5、案例操作

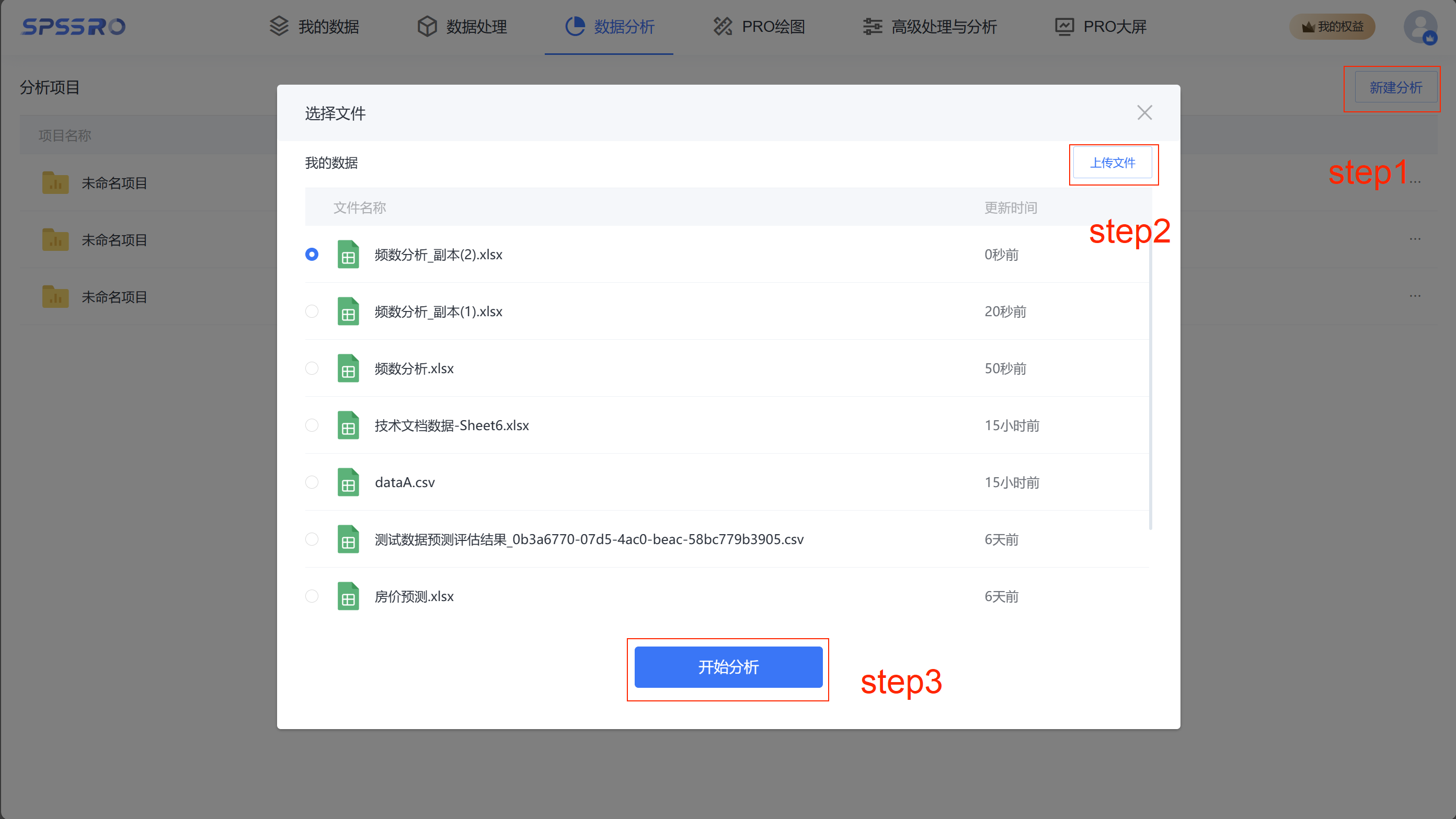
Step1：新建分析；
Step2：上传文件；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

Step4：选择【对应分析】；
Step5：查看对应的数据数据格式，【对应分析】要求特征序列为类变量，且至少有两项；
Step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：卡方交叉列联表 

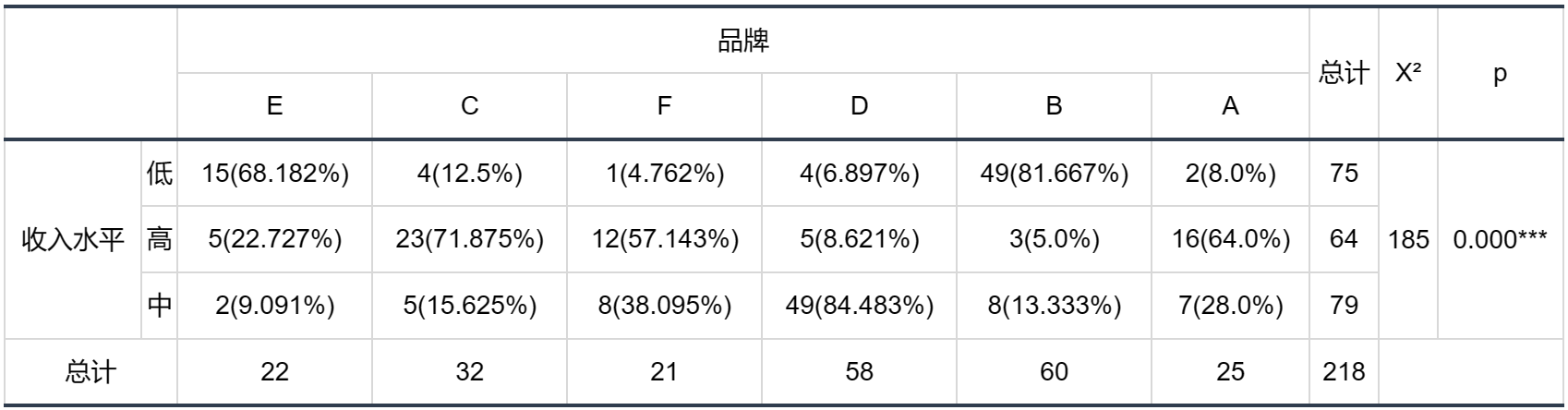
图表说明：上表为交叉列联表，展示了交叉对应表的结果，包括卡方值、显著性P等。根据卡方显著性(P < 0.05)，若呈现显著性，则目标字段（Y）与控制字段（X）有着差异关系，否则不适合做对应分析。
结果分析：交叉列联的结果显示，以变量收入为分组项，显著性 𝑝 值为 0 ，水平上呈现显著性，拒绝原假设，因此收入与品牌存在差异关系，适合做对应分析。

输出结果 2：因子分析表 

图表说明：上表为因子分析表，可以分析字段提取的维度的贡献率。维度的累计贡献率越高，表示可解释的效度与信度效果越好，一般认为累计贡献率高于 80%时，模型表现较为优秀;
奇异值：即惯量的平方根，相当于相关分析里的相关系数;
主惯量：即常说的特征根，用于说明对应分析的各个维度，能够解释列联表的两个变量之间相互联系的程度。
结果分析：惯量分析表结果显示，当维度达到 2 个的时候，累计贡献率达到 1.0，模型的表现非常优秀。

输出结果 3：维度分析表 

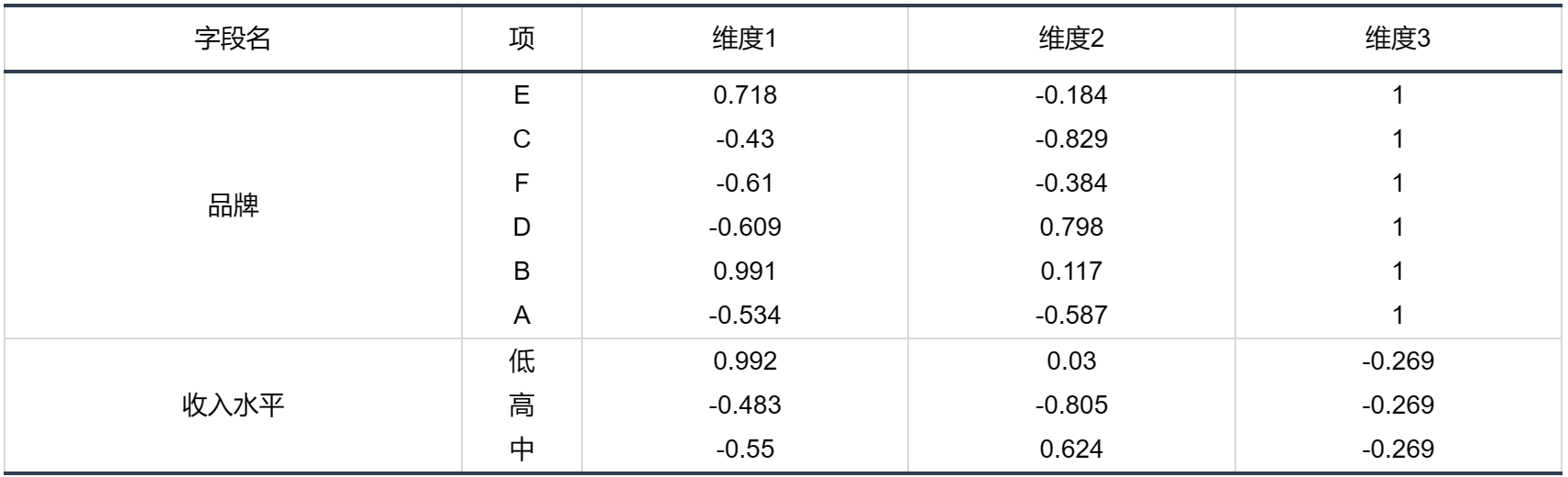
图表说明：上表为因子维度得分表，即为各个类别项在各维度上的坐标具体值，其代表各点在空间中的距离和位置可反映点之间的关系情况，用于画类别点的联合图，即可直观看出各个类别的距离。（这里列出三维度得分表，是由于可视化分析最多只支持三维，即三个主成分。）

输出结果 4：维度对应表

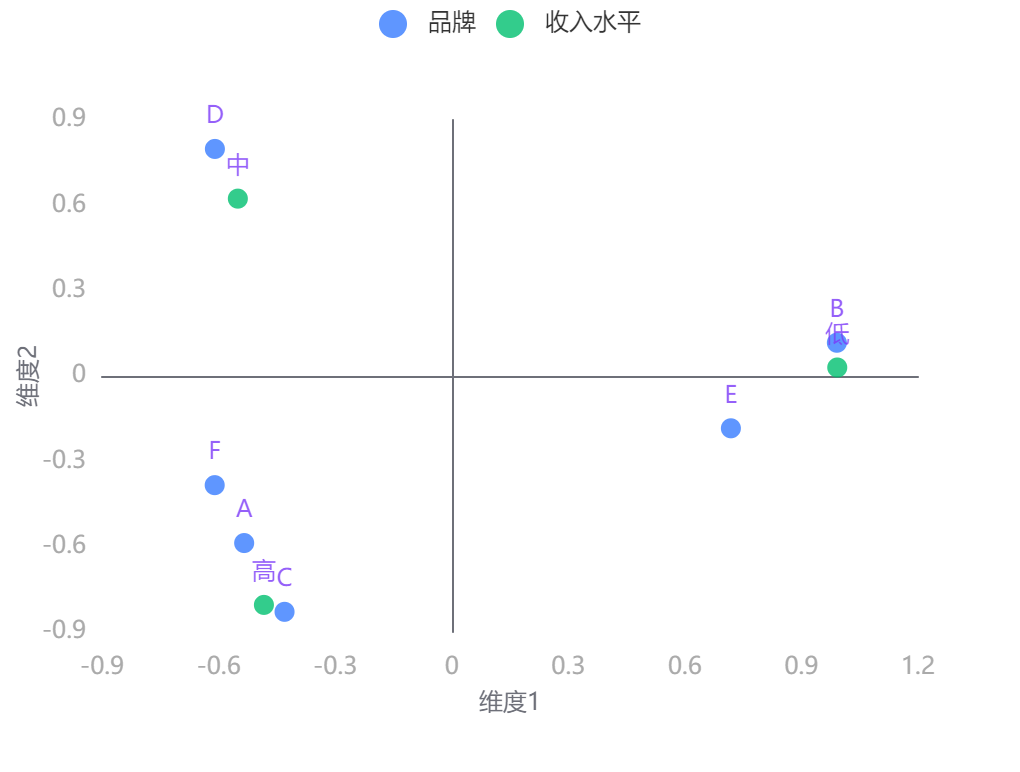
图表说明：上图为类别点的联合图，用于分析点之间的关系情况。
结果分析：由图可知，低收入人群更偏向 B、E 品牌，中收入人群更偏向 D 品牌，高收入人群更偏向 A、C、F 品牌。

# 7、注意事项

变量属性为分类变量；
对应分析的前提条件是两两定类数据之间具有相关关系。当因素间在统计学上具有显著性关联时，在此基础上使用对应分析才具有意义。可以通过 SPSSPRO-Kappa 进行相关性分析或使用SPSSSPRO-Pearson卡方检验进行独立性检验；
分析的数据至少有两行两列，且没有缺失值，不应出现负数据，所有数据必须具有相同的标度（不同标准化分析的结果不同）；
对应分析易受异常值影响；
在分析降维图时需要注意因子的总解释方差程度，如果解释度太小，分析意义不大，一般要求累计方差贡献率达到80%以上；
采用对应分析时，要注意修正一下列名与数值标签，避免太长文字导致因子载荷分布图不美观；
定性变量划分的类别越多，对应分析方法的优越性越明显。

# 8、模型理论

因子分析法分为 R 型因子分析和 Q 型因子分析。R 型因子分析研究变量（指标）之间的相关关系，Q 型因子分析研究样本之间的相关关系。有时不仅关心变量之间或样本之间的相关关系，还关心变量和样本之间的对应关系，这是因子分析方法不能解释的。

对应分析的步骤为：
（1）构造交叉列联表。设有有 n 个样本,每个样本，观测 m 个变量值,则原始数据为

$[\begin{matrix} x_{11} & x_{12} & . . . & x_{1 m} \\ x_{21} & x_{22} & . . . & x_{2 m} \\ . . . & . . . & . . . & . . . \\ x_{n 1} & x_{n 2} & . . . & x_{n m} \end{matrix}]$

式中:

x_{i j}

表示第 i 个样本的第 j 个变量.
(2) 按行、列分别求和,得行和

X_{i}

、列和

X_{j}

及总和 N.
(3) 计算原始数据的概率矩阵

P

，其中：

$P_{i j} = \frac{x_{i j}}{N}$

P_{i} . = \sum_{j = 1}^{p} P_{i j}

P . j = \sum_{i = 1}^{n} P_{i j}

如果此时满足 $P_{i j} = P_{i} . * P_{. j}$ ,那么可以进一步使用卡方检验验证变量间是否互相独立，若结论为拒绝原假设，则变量间不独立，可以进一步使用对应分析探究各状态之间的关系。

(4) 计算数据变换矩阵
将对应矩阵P进行标准化变换得到过渡矩阵Z：

z_{i j} = \frac{P_{i j} - P_{i .} P_{. j}}{\sqrt{P_{i .} P_{. j}}} (i = 1, 2, . . ., n; j = 1, 2, . ., m)

(5) R型因子分析
计算列变量的协方差矩阵 $A = Z^{T} Z$ 的特征根 $λ_{1} \geq λ_{2} \geq . . . \geq λ_{m}$ ,以及对应的特征向量 $U_{i}$ 根据累计方差贡献率（大于 70%~90%）确定最终提取特征根的个数k，并计算出相应的R型因子载荷矩阵F(因子载荷是列变量的某个分类在某个因子上的载荷，反映它们之间的相关关系),即：

F = [\begin{matrix} u_{11} \sqrt{λ_{1}} & u_{12} \sqrt{λ_{2}} & . . . & u_{1 k} \sqrt{λ_{k}} \\ u_{21} \sqrt{λ_{1}} & u_{22} \sqrt{λ_{2}} & . . . & u_{2 k} \sqrt{λ_{k}} \\ . & . & . & . \\ . & . & . & . \\ . & . & . & . \\ u_{m 1} \sqrt{λ_{1}} & u_{m 2} \sqrt{λ_{2}} & . . . & u_{m k} \sqrt{λ_{k}} \end{matrix}]

(6) Q型因子分析
计算样本的协方差矩阵 $B = Z Z^{T}$ ,B与矩阵A具有相同的非零特征根， $λ_{1} \geq λ_{2} \geq . . . \geq λ_{m}$ ,特征向量为 $V_{i} = Z U_{i}$ ,计算步骤与上述相同，算出相应的因子载荷矩阵G，根据累计方差贡献率确定最终提取特征根的个数k。

(7)在二维因子轴上作图.用同一因子轴同时样品和变量,即 R 型分析、Q 型分析同时反映在一张图上。需要注意的是，对于R型因子载荷F和Q型因子载荷G中的元素，其取值范围是相同的，且元素数量大小的含义也类似。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 高惠璇.应用多元统计分析[M].北京:北京大学出版社,2005.
[3] 董海彪,卢文喜,安永凯,等. 基于对应分析法的鄂尔多斯盆地东北部地下水污染分析[J]. 中国环境科学,2015(11):3371-3378.
[4] Eric J. Beh, Rosaria Lombardo.Correspondence Analysis[B].2014(8).DOI:10.1002/9781118762875

建议反馈