重复测量方差
# 1、作用
重复测量方差是一种用于重复测量数据的方差分析,通过分解方差-协方差矩阵代替对方差的分解。而重复测量数据,是一种医学研究常用数据,通过对不同时间点对同一对象的同一观察指标进行多次测量得到。这类数据常常存在相关性,不符合一般方差分析对数据的独立性的要求,故需要使用重复测量方差进行分析。
# 2、输入输出描述
输入:组内变量(大于等于2个)与因变量和个体变量,以及可选的组间变量。
输出:组间、组内不同水平之间是否存在差异以及组间随着组内变量的变化趋势。
# 3、案例示例
案例:某医院需要测量某试验后的血糖浓度,于是将男、女各50人分为两组,分别测量0、45、90、135分钟的血糖浓度。用重复测量方差法分析男、女(组间)之间和各个时间点之间(组内)是否存在差异。
# 4、案例数据
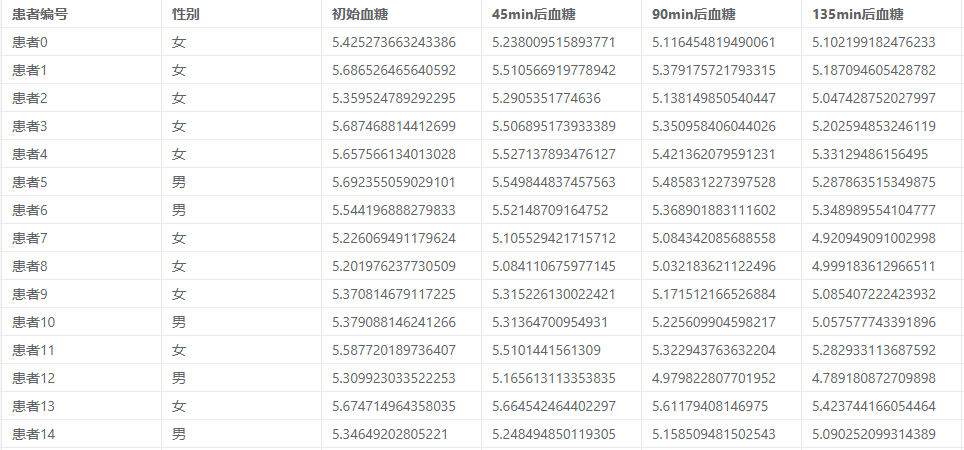
重复测量方差案例数据
# 5、案例操作
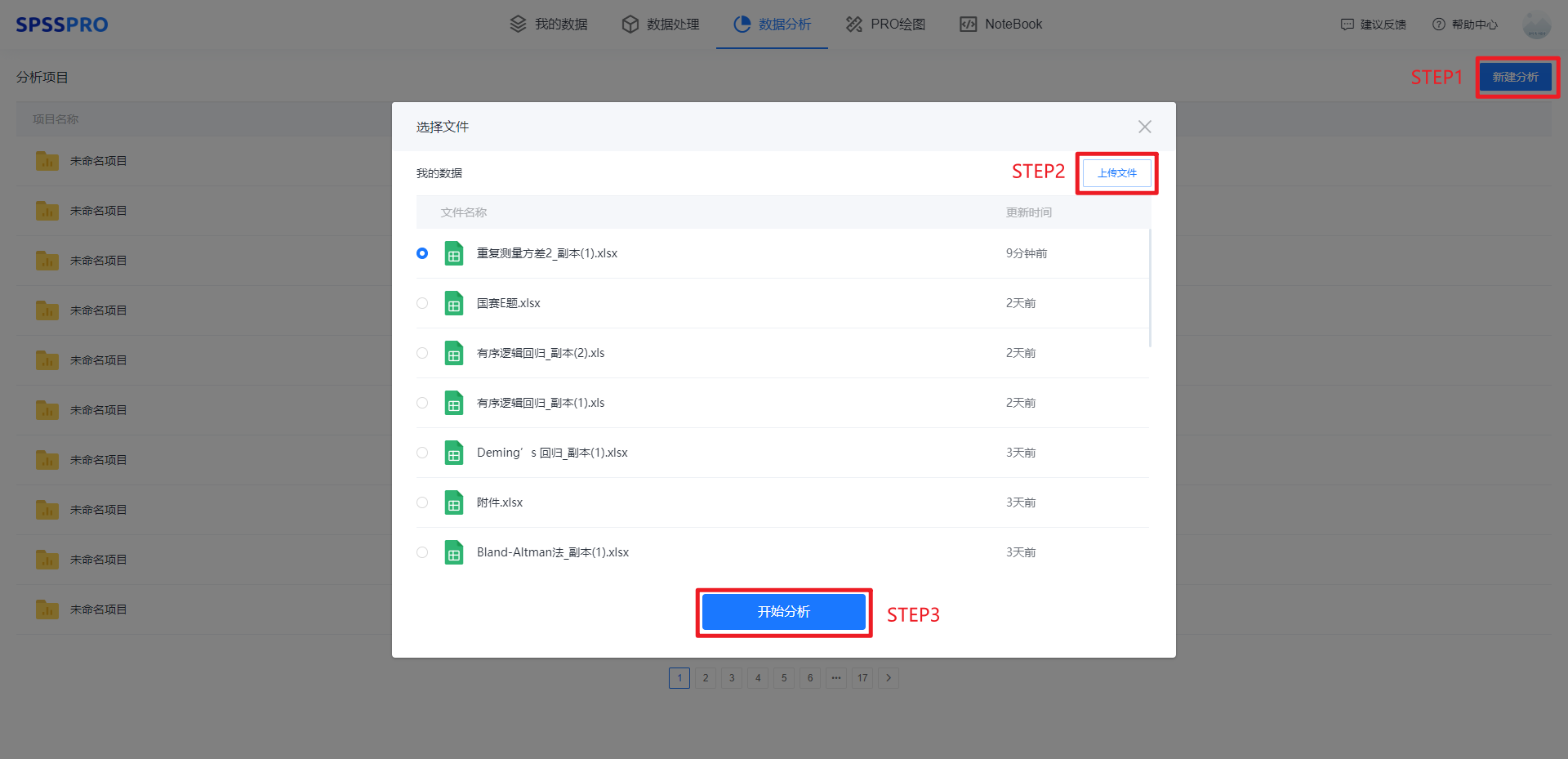
Step1:新建项目;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;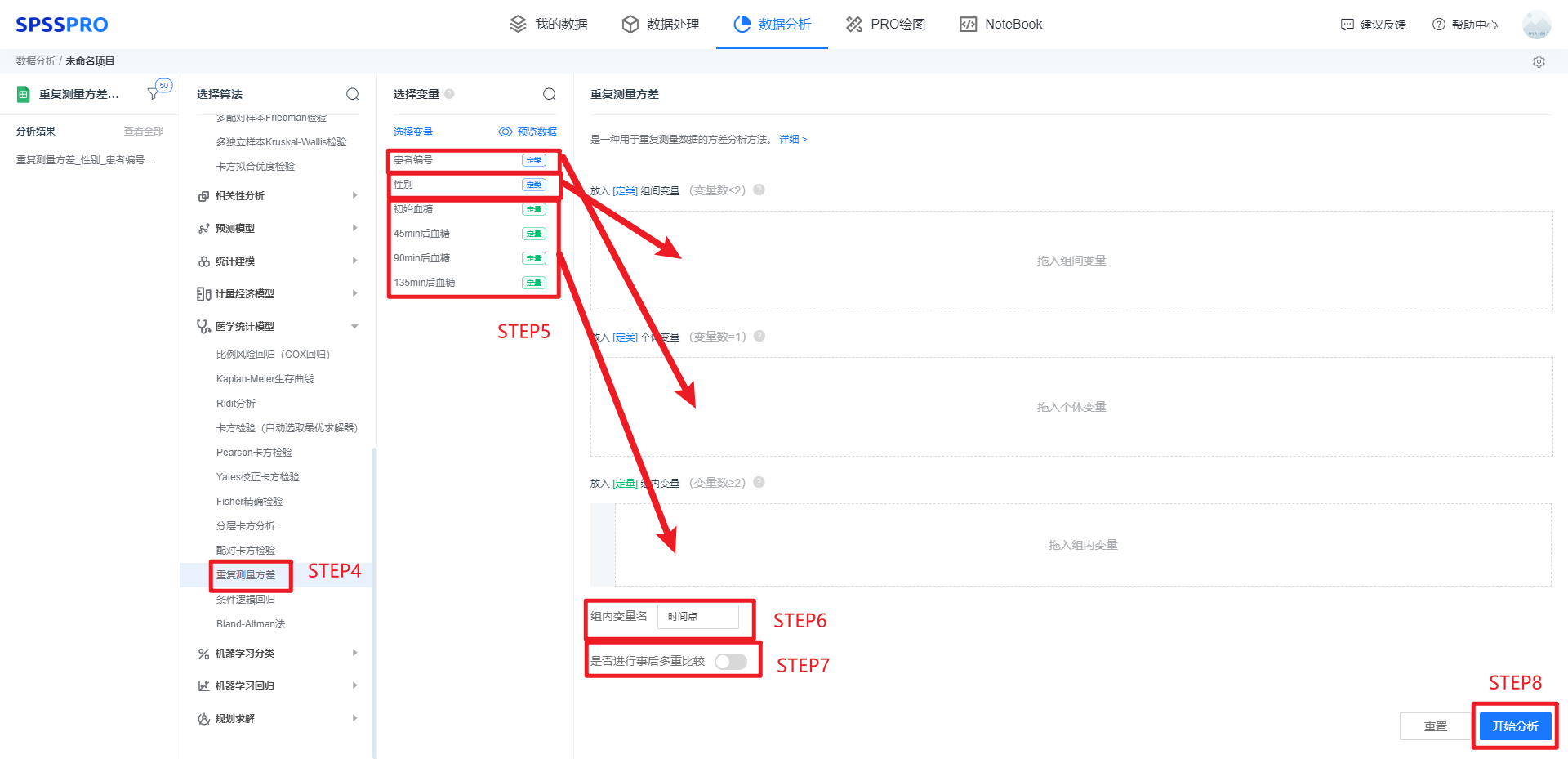
step4:选择【事后多重比较】;
step5:查看对应的数据数据格式,输入对应的个体变量和组内变量,以及可选的组间变量;
step6:输入组内变量名(只是一个代表组内变量的名字),因为是45min/90min/135min的重复测量,故为时间点(如果是如第一次测量/第二次测量/第三次测量,可以尝试取名为测量节点等名字);
step7:选择是否进行事后多重比较,本例选择不进行;
step8:点击【开始分析】,完成全部操作。
# 6、输出结果分析
输出结果1:
图表说明:
上表展示了球形度检验的结果,用于检验不同组内变量的结果是否有相关性,且组内项数量为2时,球形度检验结果失效,其中:
P>0.05,通过球形检验,在组内效应的检验中可采用球形度检验结果。
P<0.05,未能通过球形检验,重复测量的数据之间有相关性,在组内效应的检验中需要采取校正结果或者多元方差分析结果。
如若需要校正,存在两种校正方法,一种是格林豪斯-盖斯勒校正法,另一种是辛-费德勒校正法。
智能分析:
球形度检验结果显示,显著性P值为0.000***,水平上呈现显著性,未能通过球形检验,需要采取校正结果,建议采用选用格林豪斯-盖斯勒校正法。
分析:
又称球对称检验,检验数据的协方差矩阵不满足球形对称条件:
- 如果P值大于0.05为通过球形度检验,此时无需采用校正结果,后续结果直接看假设球形度这一行即可。
- 如果P值小于0.05为未通过球形度检验,此时需要采用校正结果,根据格林豪斯-盖斯勒校正法的epsilon判断,如若小于等于0.75则采用,否则采用辛-费德勒校正法。同样看对应行的结果即可。
输出结果2:组内效应分析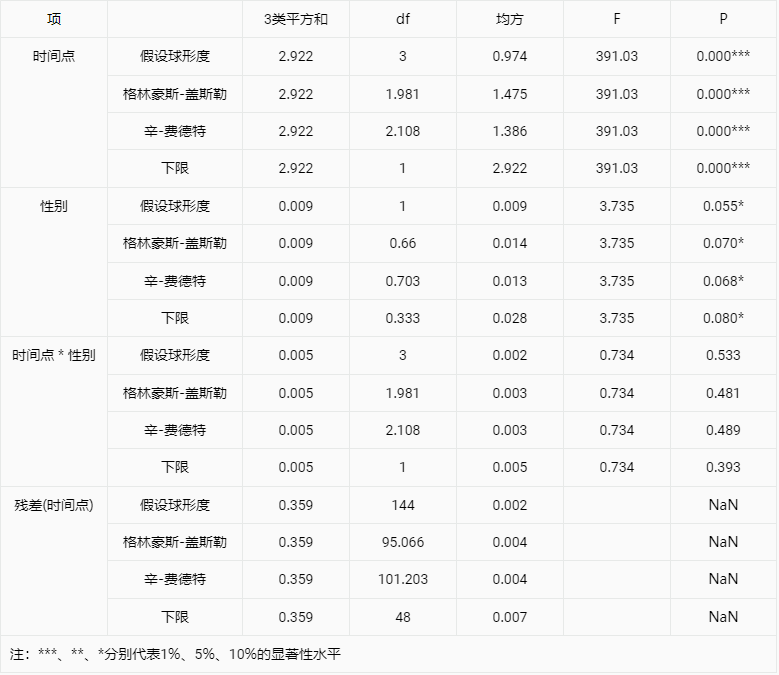
图表说明:
上表展示了组内效应分析的结果,根据是否通过球形检验,选用对应的结果进行分析。
智能分析:
对于变量时间点,选用格林豪斯-盖斯勒校正法,分析可以得到,显著性P值为0.000***,水平上呈现显著性,对结果有显著性影响,存在主效应。
对于变量性别,选用格林豪斯-盖斯勒校正法,分析可以得到,显著性P值为0.070*,水平上不呈现显著性,对结果没有显著性影响,不存在主效应。
对于交互项时间点 * 性别,选用格林豪斯-盖斯勒校正法,分析可以得到,显著性P值为0.481,水平上不呈现显著性,对结果没有显著性影响,不存在交互作用。
分析:
- 变量时间点呈现显著性,有显著性影响,可以认为存在组内效应。即某试验后,在0、45、90、135分钟的血糖浓度逐渐下降。
- 变量性别不呈现显著性,没有显著性影响,可以认为不存在组间效应。即男、女之间的性别差异,不会影响血糖浓度下降的情况。
- 变量时间点*性别呈现显著性,有显著性影响,可以认为存在交互效应。即在0、45、90、135分钟的时间流逝,男、女之间的性别差异不会影响血糖浓度下降的幅度。
- 变量残差的分析意义不是很大,仅供参考。
输出结果3: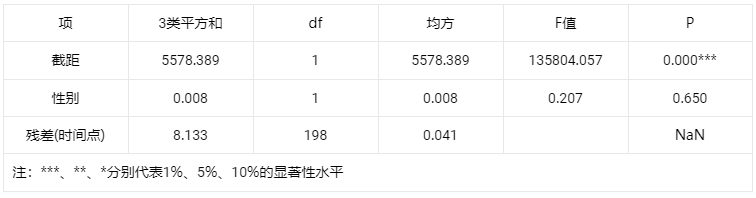
图表说明:
上表展示了组间效应分析的结果,对变量不同水平之间的具体差异进行分析。
智能分析:
对于变量性别,从F检验的结果分析可以得到,显著性P值为0.650,水平上不呈现显著性,对结果没有显著性影响,不存在主效应。
分析:
分析是否存在组间效应,分析可得,P>0.05,不呈现显著性,故不存在主效应。
输出结果4:均值对比图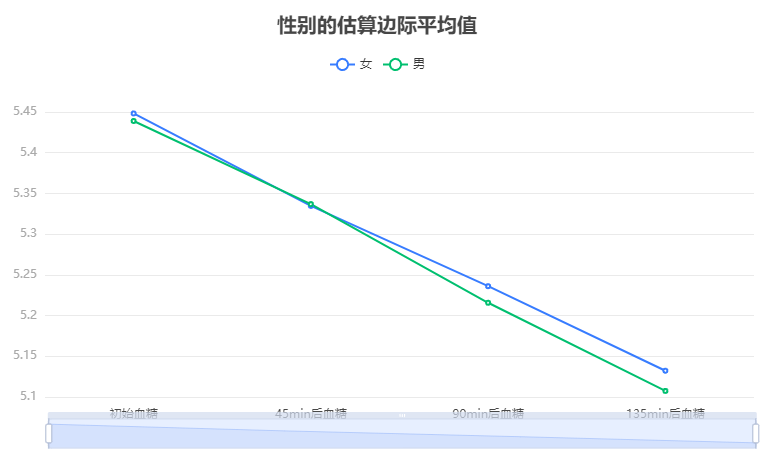
图表说明:
上图展示了重复测量方差的均值的结果,通过比较均值以及交叉情况,可以挖掘其差异关系。
# 7、注意事项
- 可以不输入组间变量,单纯进行组内变量的分析。
- 重复测量方差需要满足正态性(限制较为宽泛)和球形度假设(球形对称条件),不满足球形度假设时,需要参考校正后结果。
# 8、模型理论
# 重复测量方差介绍以及应用场景
重复测量方差是一种用于重复测量数据的方差分析,通过分解方差-协方差矩阵代替对方差的分解,下文仅介绍单因素重复测量方差分析。
重复测量方差分析的统计方法基于重复测量的实验设计。 而这种设计主要出于以下三种原因:
- 研究个体间变异很大
- 难以征募到足够多的被试
- 研究目的是考查某指标在不同时间的变化情。
如同独立测量方差分析是独立样本T检验的扩展一样,重复测量方差分析是配对T检验扩展到能容纳任何条件数的统计方法。用重复测量方差分析的统计方法取代一般单因素方差分析, 是由于重复测量方差分析自动分离出了个体差异这一误差,从而避免了由于个体差异太大导致F值太小,不接近统计显著性而不能拒绝零假设的情况。重复测量方差分析的公式如下:
# 重复测量方差分析的假设
重复测量方差分析的假设除了一个重要的假设外,与方差分析的假设实际上是一样的,有以下四个:
- 独立随机取样
- 正态分布
- 方差齐性
- 协方差齐性
当遇到只有两个处理条件时,最后一个假设并不适用。然而当配对(或重复)设计有多余两个水平时,我们可以计算每对水平的协方差。只有当所有处理水平对具有相同的协方差时,总体中才存在协方差齐性。
这最后一个假设的含义有点难于理解,而且对违反这一假设该怎么处理尚有争论。首先,如果第3和第4个假设都为真,那么总体呈现一种称为复合对称的情形。当存在复合对称时,任何一对处理水平的总体相关(ρ)和任何其他对之间的总体相关都相等。复合对称在重复测量方差分析中被满足时(连同最开始的 两个假设),就可以按公式求得临界F值,而不用担心一类错误率。
然而,复合对称是个过于严格的假设。只要方差和协方差遵循一种球形模式(球形度假设),那么第3第4个假设就可以宽松一点。
# 球形度假设的定义与检验
球形度假设较为复杂,但我们可以简单地从自变量的任何两个 水平间的交互作用量来理解这个假设:球形假设意味着所有这些 交互作用一样大。(这和要求无论你看哪一对处理水平差异值的方差都相同一样。)然而,尽管一个总体在某种程度上更可能呈球形模式而不是复合对称模式,但是对许多类型的重复测量设计, 尤其是设计时间跨度的重复测量设计,这个球形假设很少能够得到满足。综合两方面的原因,这就会出现一个严重问题。
我们很难决定是否有理由假定总体是否存在球形假设。 Mauchly(1940)设计了一种方法:用样本方差和协方差计算一个统计量W,再利用W对总体的球形假设做出推断。可是这种方法就像大多数统计检验一样,对小样本效果不好。
因此, 当数据量确实小的适合,除非数据严重偏离球形假设,否则你有可能会接受针对 Mauchly's W 检验的零假设并错误地下结论说球形假设得到了满足。然而鉴于重复测量设计违反球形假设是很常见的,不管在进行一般的重复测量方差分析之前 Mauchly's W检验的P值是多少,建议对数据进行球形度检验。
# 不满足球形度假设时的方法
在实验数据中,各种成对交互作用可以被用于计算一个称为 ε 的因子,它是对一个总体中球形程度的估计。
在球形满足时,ε为最大,即1.0;当数据完全缺乏球形时为最小,即1/ (c -1)。重复测量方差分析中的一般df成分乘以ε,然后我们用校正了的df成分来查临界F值。
计算 ε 并不简单,而且至少会有两种得到不同答案的方法。其中一种是由 Greenhouse 和 Geisser(1959)提出,而另一种不那么保守的校正方法由 Huynh 和 Fedlt(1976)设计。
当 ε 不是很偏离 1.0 时,Huynh 和 Fedlt 的方法更有检验力。
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 陈强. 高级计量经济学及Stata应用[M]. 高等教育出版社, 2010.
[3] 魏雨晨. 关于重复测量方差分析的理论介绍[J]. 心理医生, 2017, 23(036):294-296.
