竞争风险模型

# 竞争风险模型

# 1、作用

一种在原有基础上考虑了竞争风险的改进生存分析模型，在存在竞争风险的情况下传统生存分析往往会高估累积风险率。其中竞争风险是指当研究对象会发生几个结局事件，并且结局事件间互斥。

# 2、输入输出描述

输入：时间变量，状态变量，自变量X至为少一项或以上的变量。
输出：考虑了竞争风险后不同因素对生存期的影响情况。

# 3、案例示例

案例：某医院对白血病治疗进行生存分析，由于因为移植治疗法导致的死亡与复发是存在竞争风险的，故需要采用竞争风险模型进行分析。

# 4、案例数据

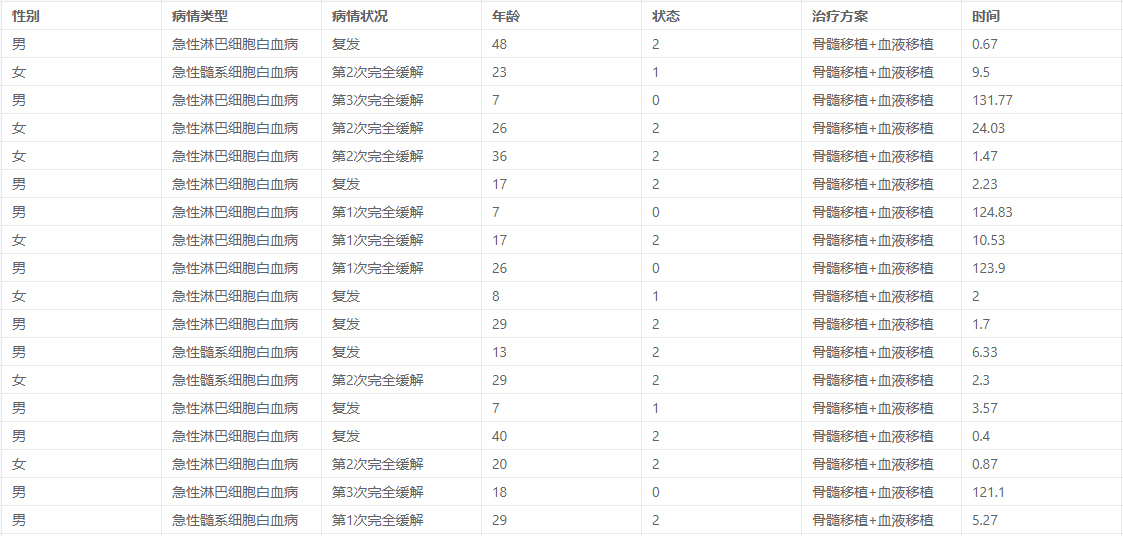
竞争风险模型案例数据

模型需要的变量为时间变量，状态变量，自变量X至为少一项或以上的变量。在案例数据中，时间变量即为时间项，代表月数。状态变量为状态项，有三种情况（0,1,2）代表删失事件（未发生任何事件），感兴趣的事件（复发）和竞争风险事件（死亡），竞争风险事件将阻止感兴趣事件的出现或影响其发生的概率，各结局事件形成"竞争”关系。性别、病情类型、病情状况、治疗方案、年龄可以作为自变量X，模型分析这些变量对生存期的影响情况。算法会根据拖入的变量数，自行判断进行单因素竞争风险模型分析和多因素竞争分析模型分析。

# 5、案例操作

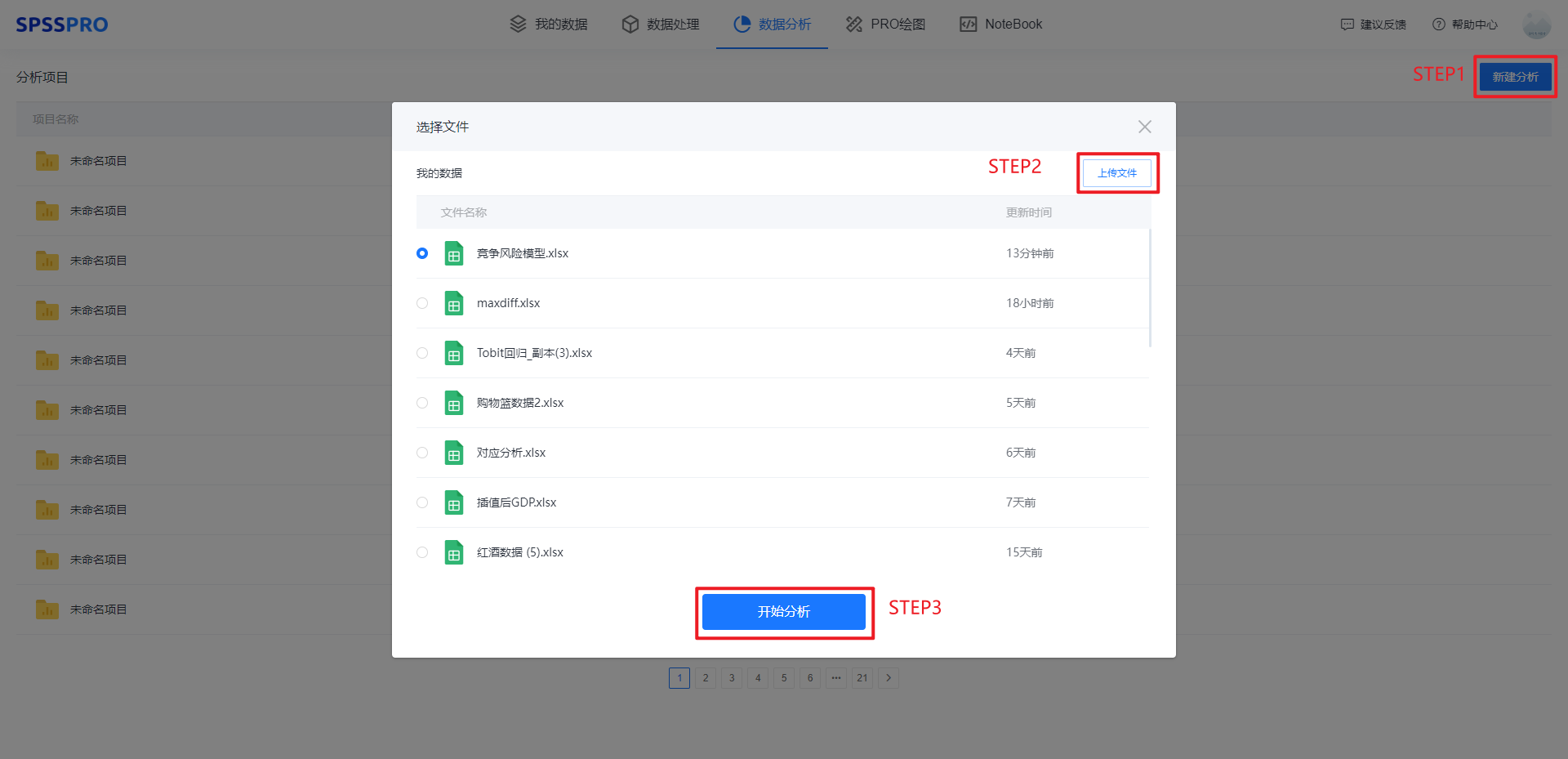
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

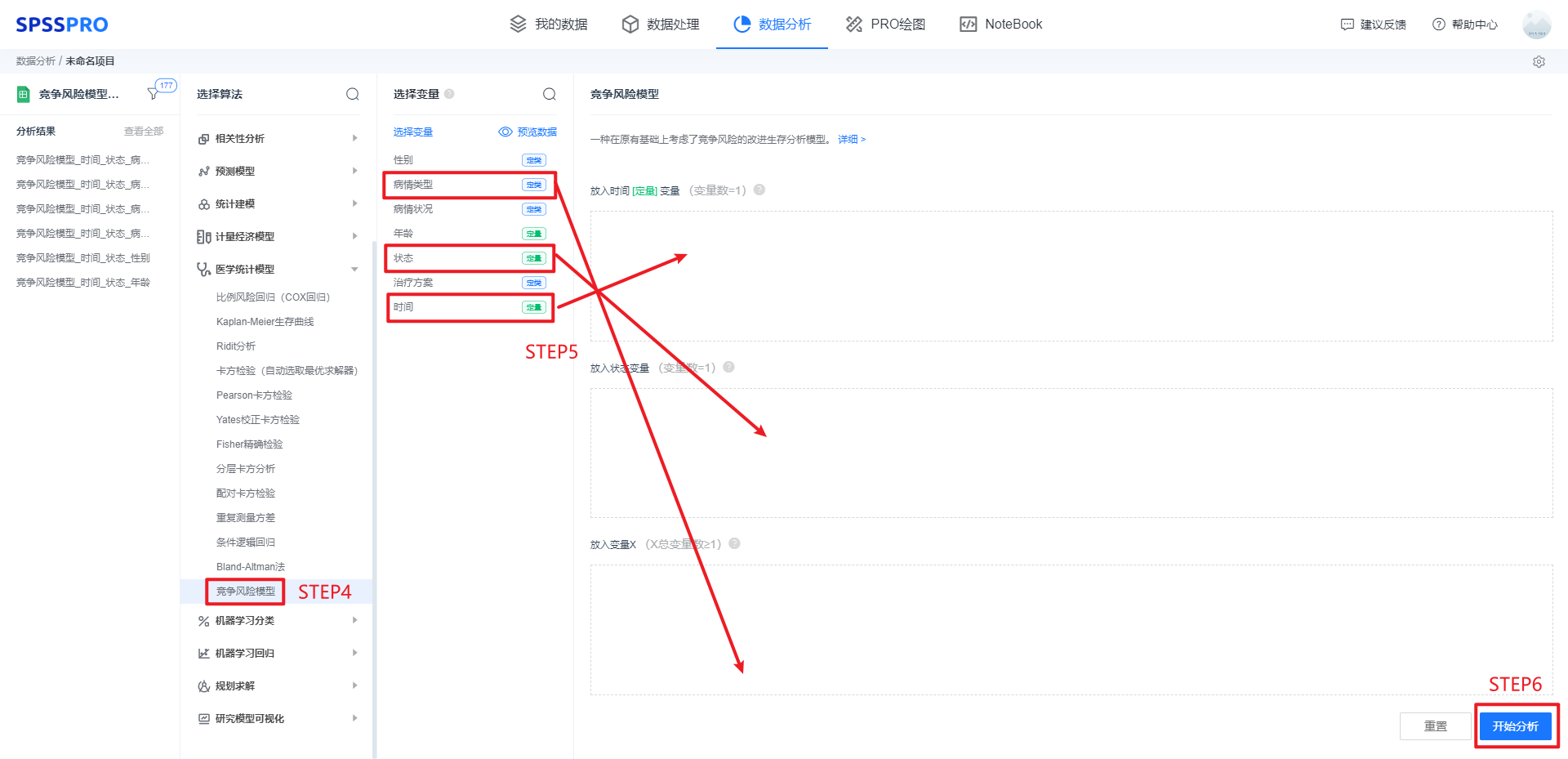
Step4：选择【竞争分析模型】；
Step5：查看对应的数据数据格式，拖入对应的选项，本例为单因素竞争风险模型，故变量X只拖入一个；
Step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果1：累积发生率函数表

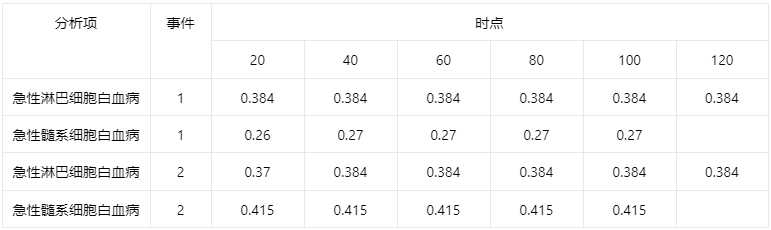
图表说明：上表展示了变量不同水平上，不同时点上的各个事件累计发生率函数值。
结果分析：在事件1上（复发，是感兴趣的主要关注事件），由表可得，急性淋巴细胞白血病比急性髓系细胞白血病更容易复发。在事件2上（死亡，也是竞争风险事件），由表可得，急性淋巴细胞白血病比急性髓系细胞白血病更不易死亡。

输出结果2：累积发生率函数图

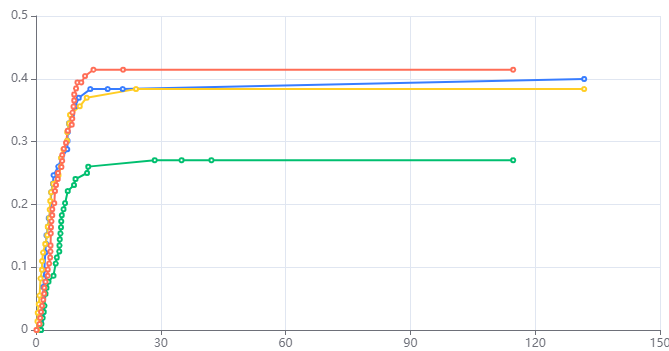
图表说明：上图以可视化的形式展示了变量不同水平上，不同时点上的各个事件累计发生率函数值。
结果分析：上图其实就是输出结果1的可视化，用于更精确的对各个事件之间累计发生率的比较，其中橙色线为急性髓系细胞白血病的竞争风险事件，黄色线为急性淋巴细胞白血病的竞争风险事件。蓝色线为急性淋巴细胞白血病的主要结局事件，绿色线为急性髓系细胞白血病的主要结局事件。

# 7、注意事项

用于区分事件发生的变量，需要注意的是，这里的三分类必须包括0、1、2，并且1代表是感兴趣的事件（如死亡/阳性等），0代表删失事件，2为竞争风险事件；
拖入的变量X数目超过一个时，会进行多因素竞争风险模型分析，此时仅有多因素竞争风险模型结果。

# 8、模型理论

Fine和Gray提出的一种部分分布的半参数比例风险模型(Fine-Gray 模型) 即为竞争风险模型(competing risks model) ，使用累积风险函数( cumulative incidence function，CIF) 来估计结局事件的累积发生概率。在该模型中，t 时刻发生事件 j 风险定义如下：

$λ_{j} (t, Z) = λ_{0} (t) e x p (\overset{´}{β_{j}} Z)$

其中

\overset{´}{β_{j}} Z

是事件j的部分分布基准风险；Z是协变量；

\overset{´}{β_{j}}

是协变量的回归系数;

e x p (\overset{´}{β_{j}} Z)

是部分分布相对风险。部分分布风险模型偏似然估计定义如下：

$L (β) = \prod_{j = 1}^{r} \frac{e x p (\overset{´}{β_{j}} Z)}{\sum_{i \in R_{j}} w_{j i} e x p (\overset{´}{β_{j}} Z)}$

风险集

R_{j}

定义如下：

$R_{j} = (i; t_{i} \geq t \lor (t_{i} \leq t Λ \in_{i} = 2))$

风险集是由在时间 t 没有发生感兴趣事件个体和在时间前发生竞争事件的个体构成。因此经历其他类型事件的个体仍在风险集中。权重定义如下:

$w_{i j} = {\begin{matrix} 1, & i f t_{i} \geq t \\ \frac{G (t)}{G (t_{i})}, & i f \in_{i} = 2 Λ t_{i} \leq t \end{matrix}$

G(t)是 Kaplan-Meier 方法估计的生存函数。时间 t 前没有发生竞争事件的个体，在时间 t 发生感兴趣事件有相等的权重(

w_{i} = 1

) ;

t_{i} ＜ t

时，发生竞争事件个体权重

w_{i} ＜ 1

。
竞争风险模型通过以下公式建立

λ_{j} (t ， Z)

与 CIF 的关系:

$I (t | Z) = 1 - e x p {- e x p (\overset{´}{β_{j}} Z) \cdot \int_{0}^{t} λ_{0} (s) d s}$

因此，通过竞争风险模型能够估计出协变量 Z 相应的系数

\overset{´}{β_{j}}

，联合累积部分分布基准风险预测特定时间个体发生感兴趣事件发生概率，即绝对风险。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 李海彬, 李霞, 王安心,等. 竞争风险模型及其在Stata软件实现[J]. 中国卫生统计, 2016, 33(5):4.

建议反馈