概率单位回归(剂量分析)
# 概率单位回归(剂量分析)
# 1、作用
是一种使用概率单位回归来对刺激强度和响应比例之间关系进行分析的方法。比如研究细菌剂量与杀死小白鼠数量的关系和对应的半数致死量,进而对毒力进行测定。其中,半数致死量指的是药物或者微生物能引起试验动物 50%死亡的剂量。
# 2、输入输出描述
输入:定量的响应数、总数量、剂量,以及可选的定类分组变量。
输出:刺激强度和反映比例之间的关系以及半数致死量。
# 3、案例示例
示例:在三次实验中,对鼠疫菌进行毒力测定,并且需要测算鼠疫菌的半数致死量。
# 4、案例数据
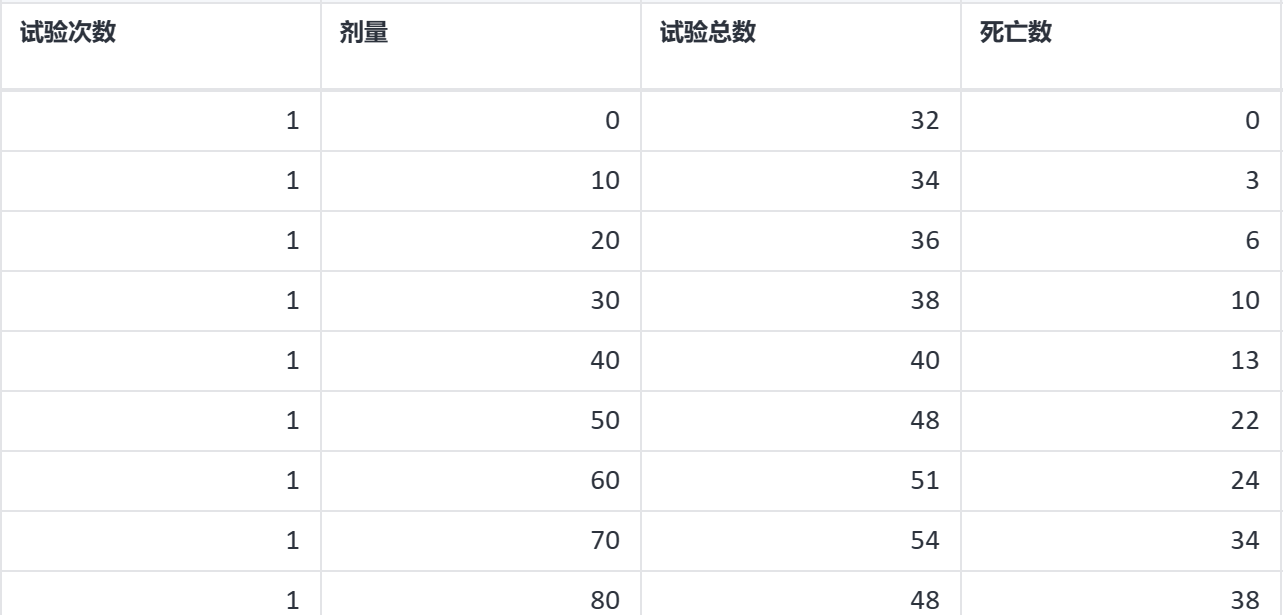
概率单位回归案例数据
# 5、案例操作
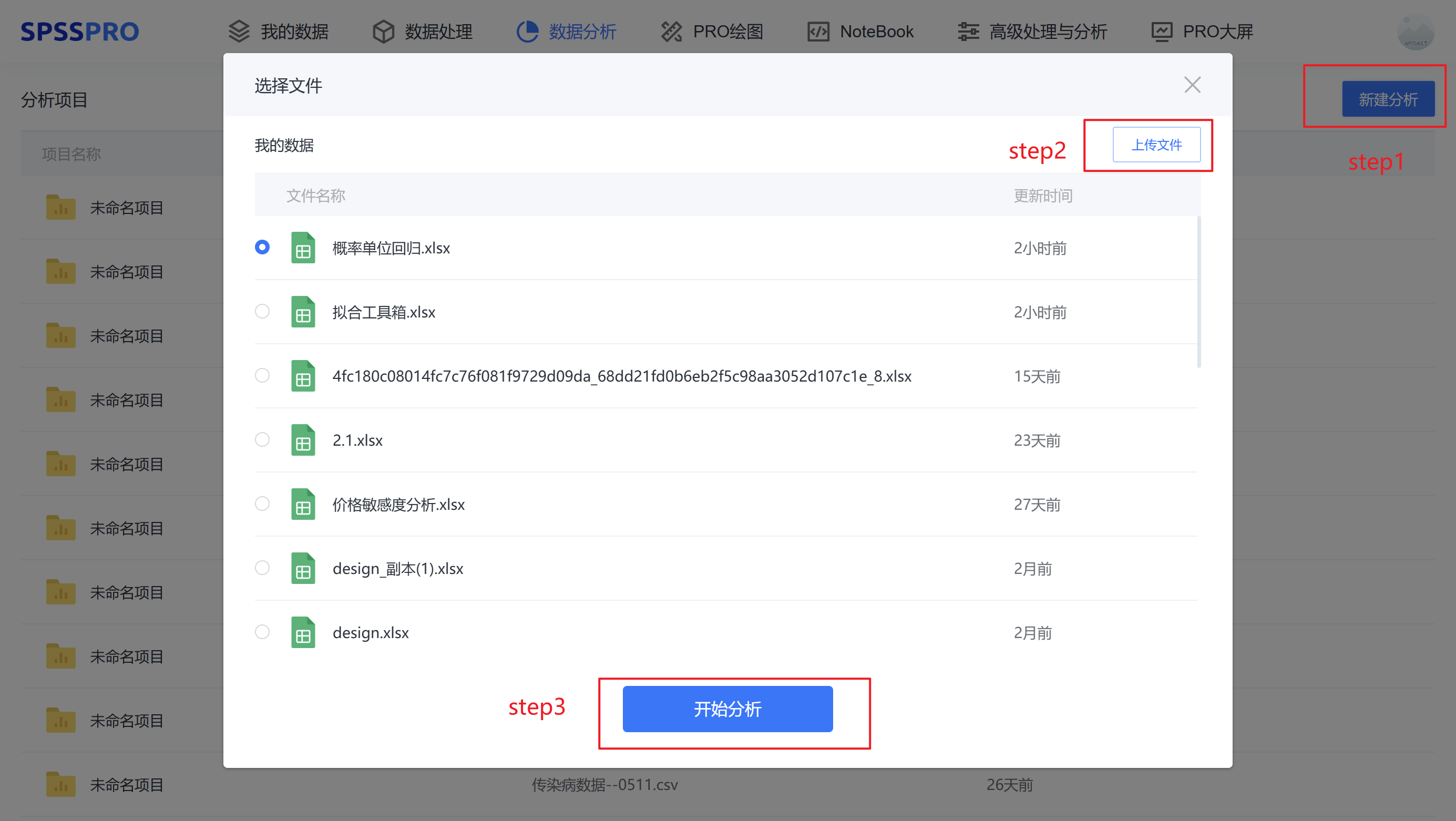
Step1:新建分析;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;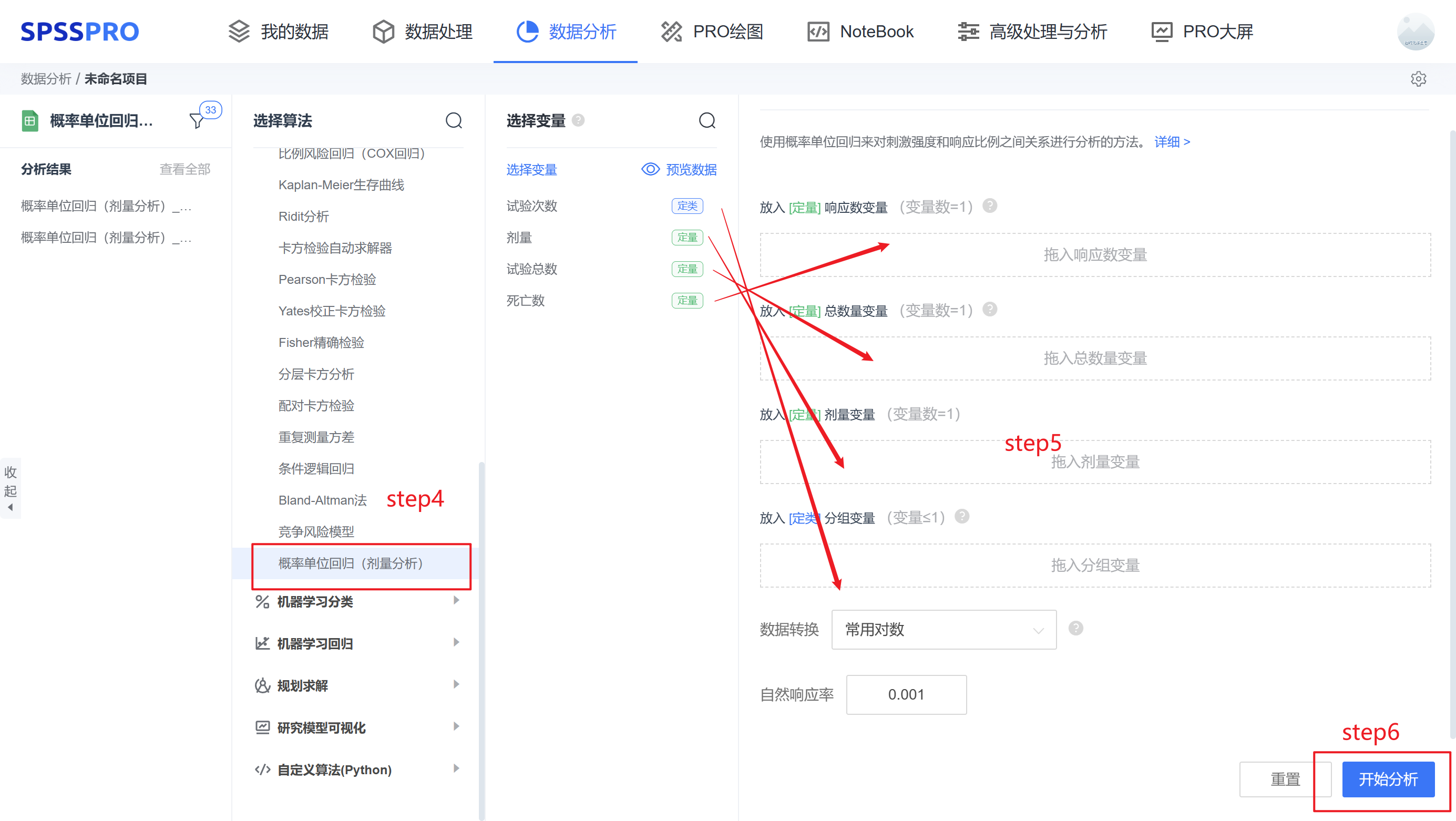
Step4:选择【概率单元回归】
Step5:查看对应的数据格式,选择所要研究的【概率单元回归】的变量数据;
Step6:点击【开始分析】,完成操作。
# 6、输出结果分析
输出结果 1:自然响应率
| 估算值 |
|---|
| 0.001 |
图表说明:上表展示自然响应率,体现在刺激强度(剂量)为 0 的时候的响应比例。
输出结果 2:皮尔逊拟合优度检验
| 卡方值 | 自由度 | P 值 |
|---|---|---|
| 51.244 | 28 | 0.005*** |
图表说明:上表展示了皮尔逊拟合优度检验结果,对 P 值进行分析,如果该值大于 0.05,则说明模型有效;反之则说明模型无效。模型的皮尔逊拟合优度检验结果显示,显著性 P 值 0.005***,水平上存在显著性,拒绝原假设,因而模型是有效的。
输出结果 3:概率单位回归结果
| 项 | 系数 | 标准误差 | Z 值 | P 值 | 系数 95%置信区间 | |
|---|---|---|---|---|---|---|
| 上限 | 下限 | |||||
| 剂量 | 2.699 | 0.163 | 16.585 | 0.000*** | 3.018 | 2.38 |
| [ "常量", 1 ] | -4.543 | 0.291 | -15.605 | 1.000 | -3.972 | -5.114 |
| [ "常量", 2 ] | -4.667 | 0.293 | -15.937 | 1.000 | -4.093 | -5.241 |
| [ "常量", 3 ] | -4.541 | 0.291 | -15.594 | 1.000 | -3.971 | -5.112 |
图表说明:模型的公式为:
1.0:Probit(p) = -4.543 - 2.699092712184579 _ (剂量)
2.0:Probit(p) = -4.667 - 2.699092712184579 _ (剂量)
3.0:Probit(p) = -4.541 - 2.699092712184579 * (剂量)
剂量项显著性 P 值为剂量,水平上呈现显著性,拒绝原假设,因此剂量项系数显著。
截距项字段 1.0、2.0、3.0 显著性 P 值为 1.000,水平上不呈现显著性,不能拒绝原假设,因此截距项系数不显著。
1.0、2.0、3.0 分别代表着三次实验,说明三次实验对死亡率并没有差异。
输出结果 4:模型路径图 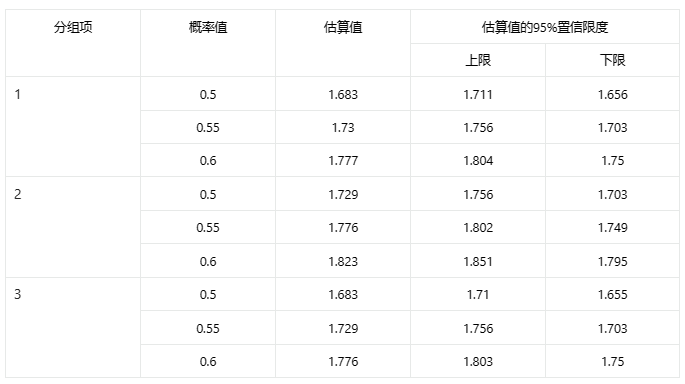
图表说明:上表展示置信限度表,表示在不同响应概率下所对应的刺激强度(剂量)。可以对不同分组项的剂量的响应率进行对比。比如上面表格中就保留了概率值为 0.5-0.6 的数据。由此可以观察分组 1 和分组 2 的估算值(这个估算值就相当于剂量)分别为 1.683、1.729,说明若想要有 0.5 的致死率,分组 1 的剂量比分组 2 的剂量低点也可达到要求,说明分组 1 实验中更容易致死率更高。
# 7、注意事项
- 若是对数据进行转换后,在分析结果的时候,同时也要剂量值进行转换后再做解释。
# 8、模型理论
概率单位回归(Probability Unit Regression,PUR)是一种用于剂量-反应分析的统计方法,常用于生物学、毒理学、环境科学等领域。PUR 的主要原理是使用概率单位替代传统的实际剂量单位,使剂量-反应关系在不同试验中可比较。
在传统的剂量-反应分析中,我们通常使用实际剂量单位(例如:mg/kg、ppm 等)来描述剂量,而反应通常用某种指标(例如:生物效应、死亡率、发病率等)来度量。然而,由于不同试验的剂量单位和测量指标可能不一样,导致了不同试验结果难以直接比较。
PUR 通过将剂量和反应转换为概率单位,使得不同试验的结果可以在同一尺度上进行比较。其基本思想是将实际剂量与发生反应的概率联系起来,将剂量-反应关系转换为概率-反应关系。
PUR 的具体步骤如下:
- 数据转换:将实际剂量和对应的反应数据进行转换,得到概率单位的数据。
- 概率单位计算:根据转换后的概率单位数据,计算剂量对应的概率值。
- 建立概率-反应模型:使用概率单位数据建立概率-反应模型,通常使用 Logistic 回归模型来描述剂量和概率之间的关系。
- 参数估计:利用最大似然估计等方法,估计概率-反应模型中的参数。
- 剂量估计:通过概率-反应模型,估计对应特定概率值的剂量,或者估计对应特定剂量的概率。
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com. [2] 熊浩明, 魏柏青, 魏荣杰,等. 用 SPSS 软件计算鼠疫菌半数致死量(LD50)[J]. 中国人兽共患病学报, 2013, 29(011):1127-1130.
