Pearson卡方检验
# 1、作用
Pearson 卡方检验是最有名的卡方检验之一,主要是比较定类变量与定类变量之间的差异性。包括适配度检验和独立性检验,这里默认为独立性检验,适配度检验见 SPSSPRO【卡方拟合优度检验】。
# 2、输入输出描述
输入:一个定类变量 X(如学校字段,包括甲学校、乙学校)与定类字段 Y(如甲学校 40 名学生与乙学校 60 名学生的体育成绩等级)。
输出:模型检验的结果,如甲学校与乙学校的学生体育成绩等级存在/不存在显著性差异。
# 3、案例示例
案例:分析班级(定类变量)与分科意向(定类变量)是否有显著性差异。
# 4、案例数据

# 5、案例操作
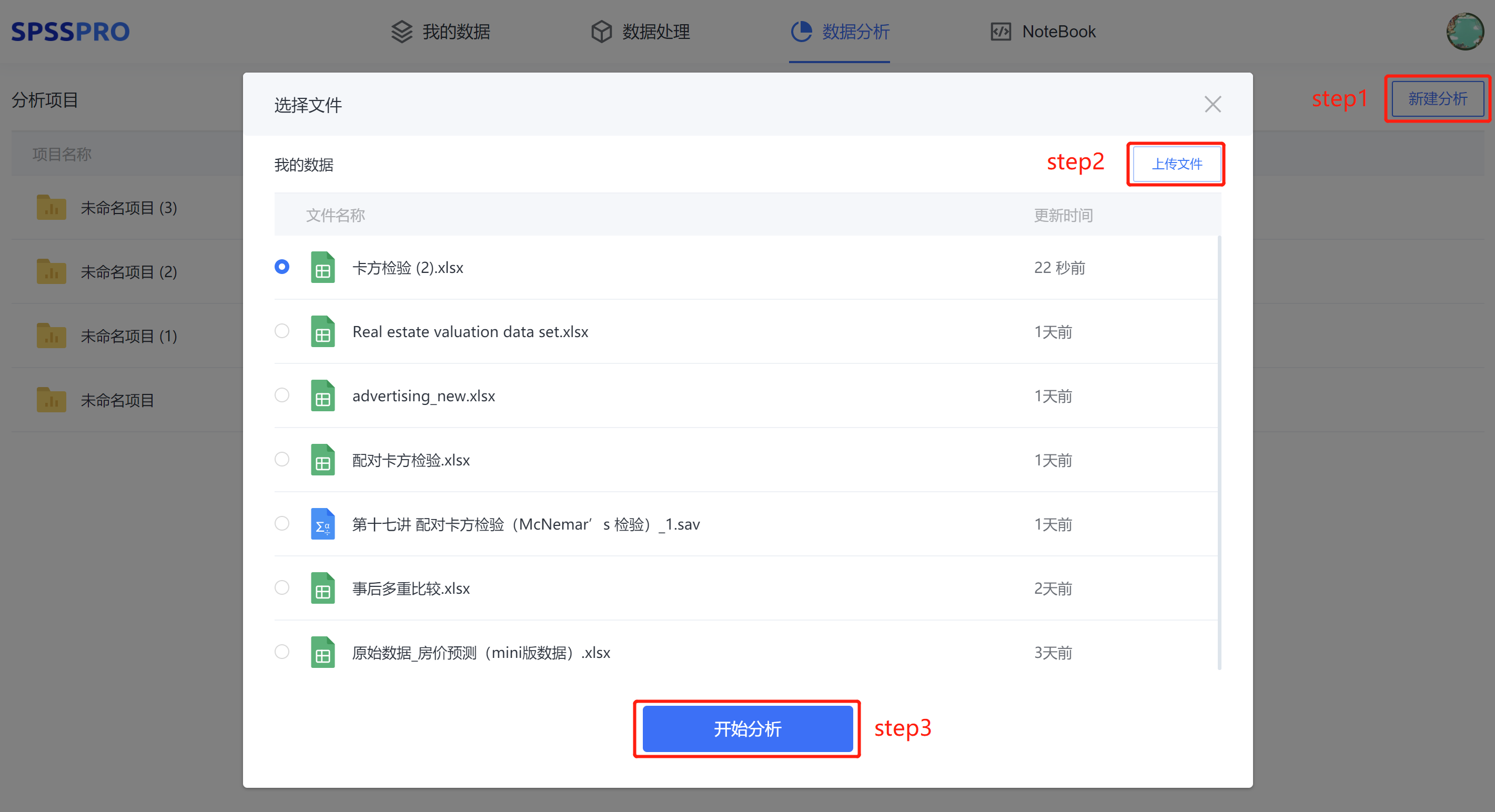
Step1:新建项目;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;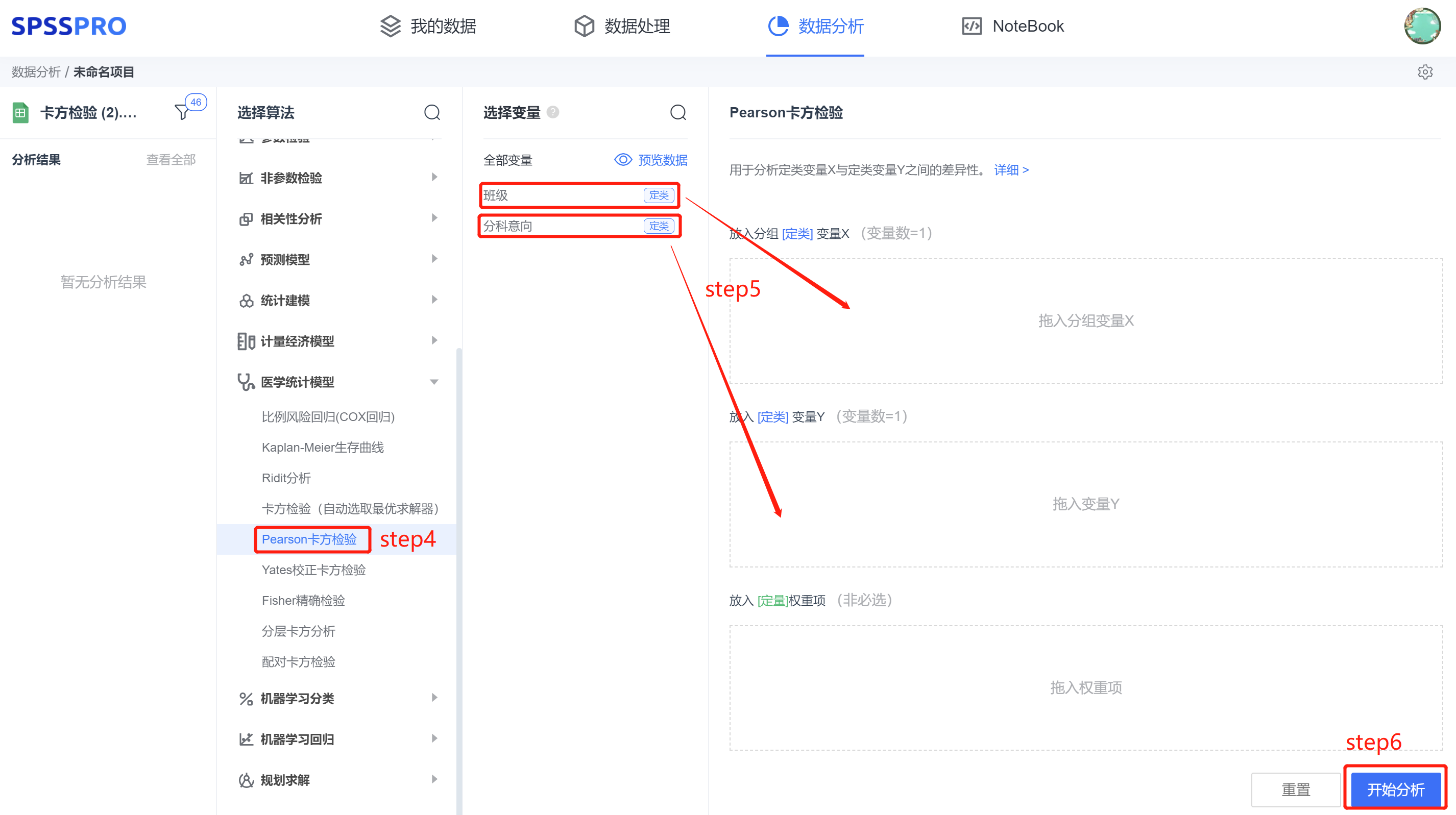
step4:选择【Pearson 卡方检验】;
step5:查看对应的数据数据格式,【Pearson 卡方检验】要求输入数据为一个定类变量 X 和另一个定类变量 Y;
step6:点击【开始分析】,完成全部操作。
# 6、输出结果分析
输出结果 1:Pearson 卡方检验结果
| 题目 | 名称 | 班级 | 合计 | 卡方值 | p 值 | |
|---|---|---|---|---|---|---|
| 一班 | 二班 | |||||
| 分科意向 | 文科 | 8 | 16 | 24 | 3.069 | 0.080* |
| 理科 | 13 | 9 | 22 | |||
| 合计 | 21 | 25 | 46 |
注:*、**、***分别代表 1%、5%、10%的显著性水平
图表说明:上表展示了 Pearson 卡方检验的结果,包括数据的频数、卡方值、显著性 P 值。
● 若 p<0.05,呈现显著性,拒绝原假设,则说明分类变量 X 与分类变量 Y 之间存在显著性差异。
● 若 p>=0.05,呈现显著性,拒绝原假设,则说明分类变量 X 与分类变量 Y 之间不存在显著性差异。
分析:Pearson 卡方检验分析的结果显示,显著性 P 值为 0.080*,水平上不呈现显著性,不能拒绝原假设,因此班级和分科意向数据不存在显著性差异。
输出结果 2:交叉列联表热力图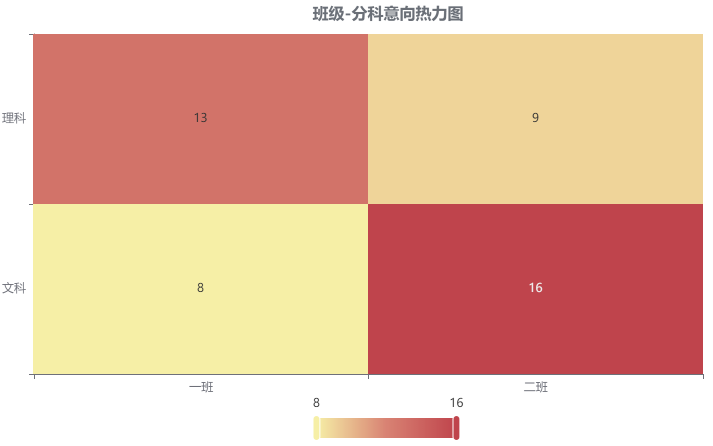
图表说明:上图展示了热力图的形式展示了交叉列联表的值,主要通过颜色深浅去表示值的大小。
输出结果 3:效应量化分析
| 字段名/分析项 | Phi | Crammer‘s V | 列联系数 | lambda |
|---|---|---|---|---|
| 分科意向-班级 | 0.258 | 0.258 | 0.25 | 0.227 |
图表说明:上表展示了效应量化分析的结果,包括 phi、Crammer's V、列联系数、lambda ,用于分析样本的相关程度。
1. 当呈现出显著性差异(前提),结合分析效应量指标对差异性进行量化分析;
2. 效应量化指标反映的是变量之间的相关程度;
3. 根据交叉类型的不同,可以选用不同的效应量指标。(交叉类型表示:交叉表横向格子数 × 纵向格子数);
4. phi 系数: phi 相关系数的大小,表示两样本之间的关联程度。当 phi 系数小于 0.3 时,表示相关较弱;当 phi 系数大于 0.6 时,表示相关较强。(用于 2×2 交叉类型表);
5. Cramer's V: 与 phi 系数作用相似,但 Cramer's V 系数的作用范围较广。当两个变量相互独立时,V=0,当数据中只有 2 个二分类变量时,Cramer's V 系数的结果与 phi 相同(若 m≠n,建议使用 Cramer's V );
6. 列联系数:简称 C 系数,用于 3×3 或 4×4 交叉表,但其受行列数的影响,随着 R 和 C 的增大而增大。因此根据不同的行列和计算的列联系数不便于比较,除非两个列联表中行数和列数一致;
7. lambda:用于反应自变量对因变量的预测效果,一般情况下,其值为 1 时表示自变量预测因变量效果较好,为 0 时表明自变量预测因变量较差(X 或 Y 有定序数据时,建议使用 lambda)。
分析:效应量化分析的结果显示,分析项:分科意向 Cramer's V 值为 0.258,因此班级和分科意向的差异程度为中等程度差异。
# 7、注意事项
- 如果个别字段的期望次数太低,会使机率分配无法近似于卡方分配。一般要求:自由度 df>1 时,期望次数小于 5 的字段不多于总字段的 20%;
- 若自由度 df=1,且若期望次数<10,则近似于卡方分配的假设不可信。此时可以将每个观察值的离差减去 0.5 之后再做平方,即叶氏连续性修正。
# 8、模型理论
1.简介
皮尔森卡方检验是最有名卡方检验之一。可用于两种情境的变项比较:适配度检验和独立性检验。当提及卡方检验而没有特别指明类型时,通常即指皮尔森卡方检验。
- 独立性检验:验证从两个变量抽出的配对观察值组是否互相独立。
- 适配度检验:验证一组观察值的次数分配是否异于理论上的分配。详见 SPSSPRO【卡方拟合优度检验】。
2.独立性检验
在同一个个体(例如:同一个人)身上有两个二元变量(X, Y),例如 X(男/女)和 Y(文科/理科),观察两个变量的相关性。虚无假设是:两个变量呈统计独立性。
在本例中:性别与选科是独立事件。
首先,每个观察值(每个抽出的人)会被重新编排到二维表(列联表)里。本例的列联表是 2×2 的构造:
| 男 | 女 | 总计 | |
|---|---|---|---|
| 文 | 43 | 44 | 87 |
| 理 | 9 | 4 | 13 |
| 总计 | 52 | 48 | 100 |
如果列联表共有 r 行 c 列,那么在独立事件的假设下,每个字段的“理论次数”(或期望次数)为:
其中 N 是样本大小(观察值的个数,亦即 2×2 列联表所有字段的总和,本例:N = 100)。本例的各字段期望值如下(括号里的数字):
| 男 | 女 | 总计 | |
|---|---|---|---|
| 文 | 43 (45.24) | 44 (41.76) | 87 |
| 理 | 9 (6.76) | 4 (6.24) | 13 |
| 总计 | 52 | 48 | 100 |
统计值的公式是:
本例统计值
因为虽然总共要计算
在本例中,在
的条件下,得出卡方分配右尾机率 p=0.1825,无法拒绝虚无假设,亦即:无法拒绝性别变量与选科变量互相独立的假设。
3.步骤:
(1)计算卡方检验的统计值:把每一个观察值和理论值(期望值)的差做平方后、除以理论值、再加总:
(2)计算统计值的自由度。
(3)依据研究者设定的置信水准,查出自由度为 df 的卡方分配临界值,比较它与第 1 步骤得出的统计值,推论能否拒绝虚无假设。
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
