条件逻辑回归

# 1、作用

条件逻辑回归是使用配对数据的一种模型，常用于医学研究的回顾研究和前瞻研究。在配对数据使用非条件逻辑回归常高估了OR值，而条件逻辑回归考虑到了数据的分层和匹配情况，从而解决这个问题。其中配对数据一般是具有特定条件或属性的病例受试者与没有该条件的n个对照受试者相匹配而组成的。

# 2、输入输出描述

输入：因变量Y为二分类定类变量，自变量X至少为一项或以上的定量变量或定类变量。
输出：条件逻辑回归系数估计以及分类预测的效果评价。

# 3、案例示例

示例：如调查痛风发病（发病为1）和三种因素(是否高尿酸血症(有病为1)、锻炼情况(不锻炼=0，偶尔=1，经常锻炼=2)、体重)的关系。采用1：2配对的病例对照研究形式，选取健康进行对照。使用条件逻辑回归进行原因分析。

# 4、案例数据

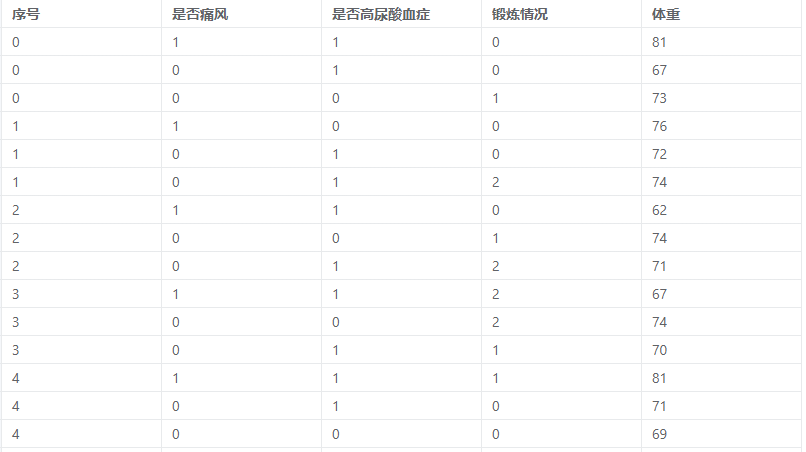
条件逻辑回归案例数据

注：
配对编号变量的意义是为配对数据进行标记，配对数据一般是具有特定条件或属性的病例受试者与没有该条件的n个对照受试者相匹配而组成的。本算法能够使用的配对数据的形式如下：

同一个序号出现最少两次；
配比相同（配对组号出现相同的重复次数，比如一个组号出现3次，就是1：2。不能出现混杂情况，比如1:2,1:3同时出现）。

如案例数据中：

序号（案例数据的序号列）以按列的顺序看，是为000/111/222/333不断重复，这代表是0/1/2/3组的数据。
而配比则看二分类0-1变量Y（案例数据的是否痛风列）的值，1个痛风病患配对2个没有患痛风的病患，这就是1:2。

# 5、案例操作

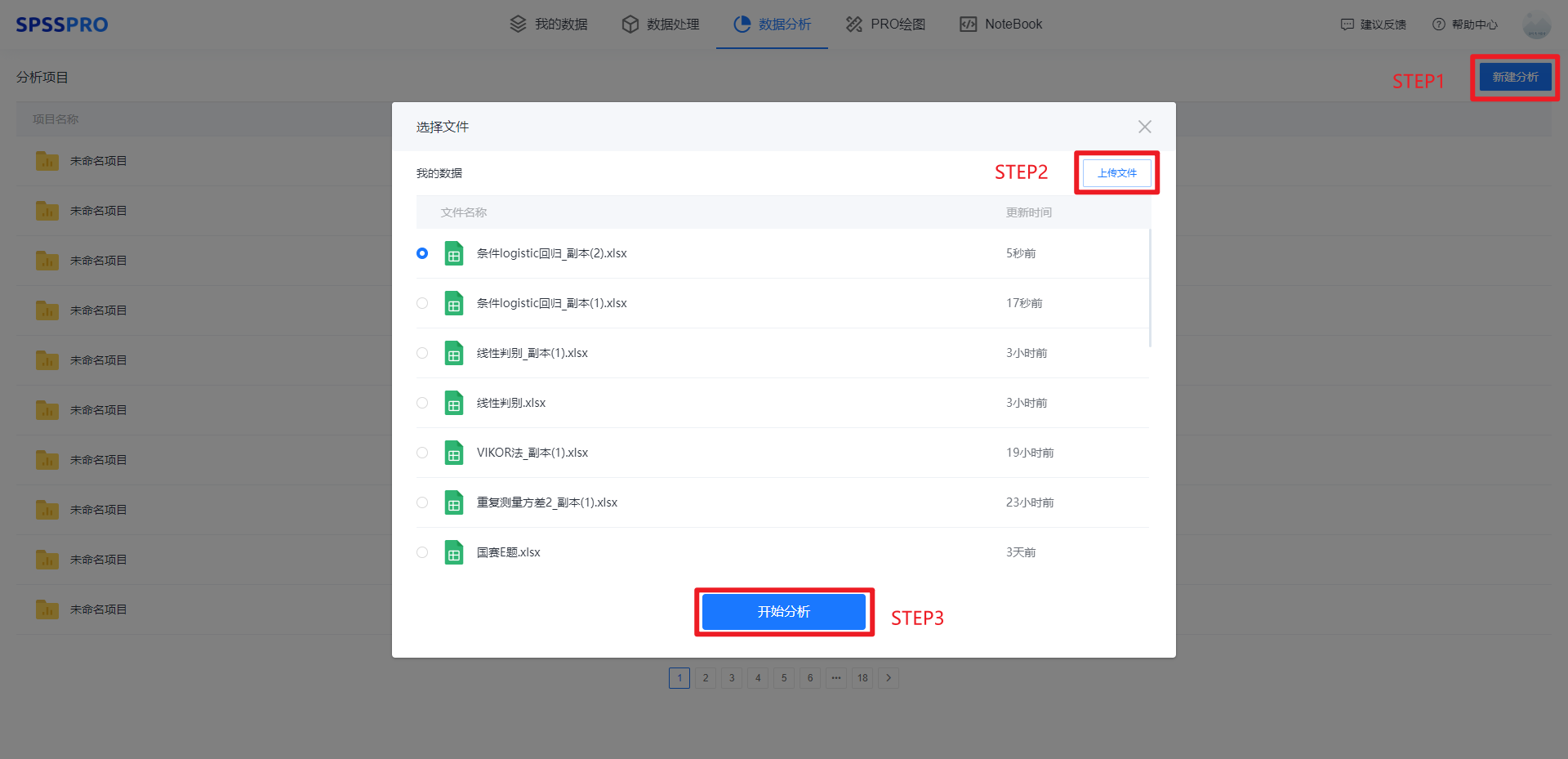
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；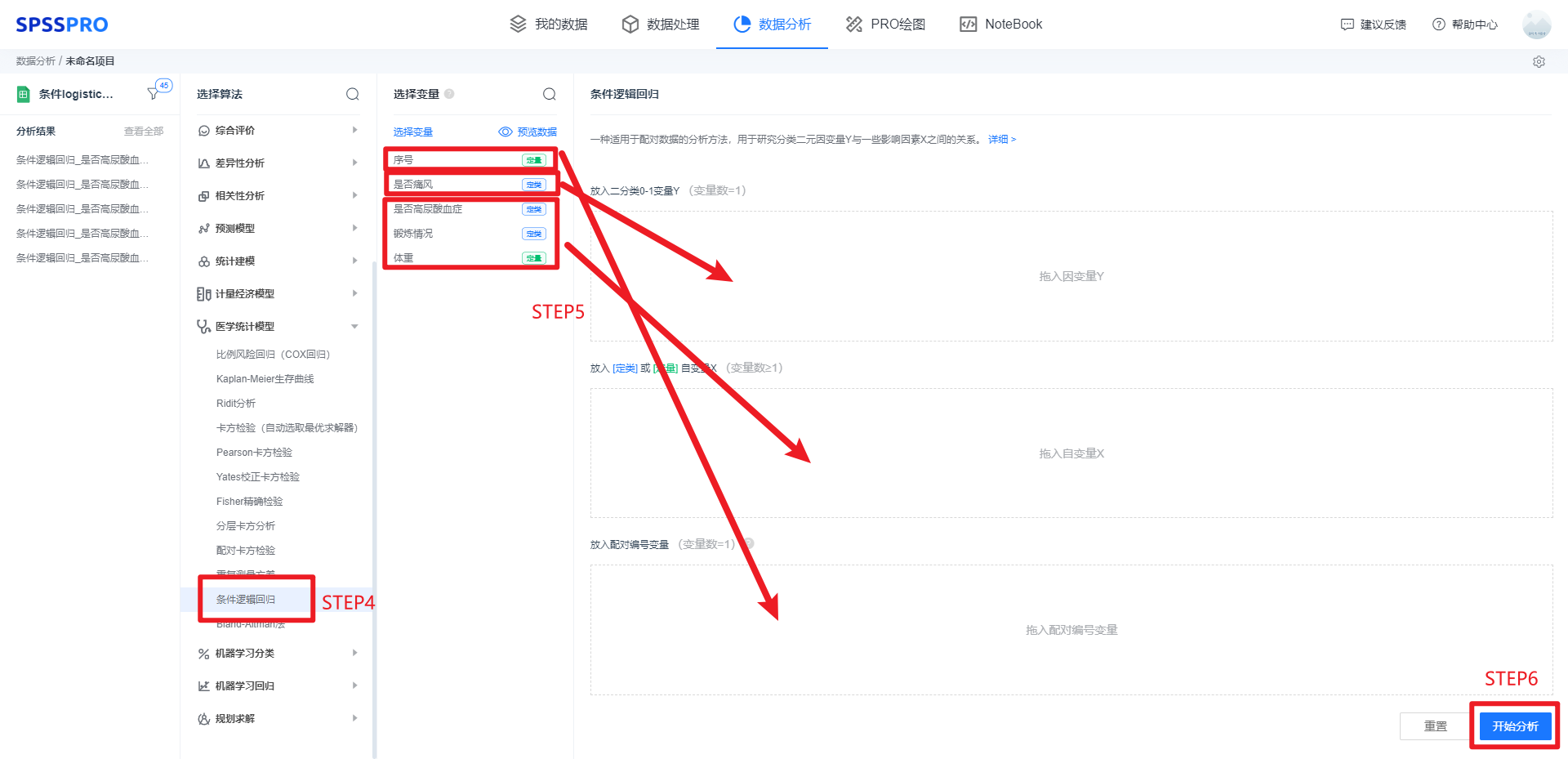

step4：选择【条件逻辑回归】；
step5：查看对应的数据数据格式，按要求输入【条件逻辑回归】数据;
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果1：多分类因变量基本汇总

图表说明：
上表展示了样本 Ominbus全局性检验的结果，包括-2倍对数极大似然值、卡方值等，用于检验模型中所有变量的回归系数是否全为零。-2倍对数极大似然值用于检验模型的拟合情况，其值越小，表示模型拟合的越好。

输出结果2：条件逻辑回归结果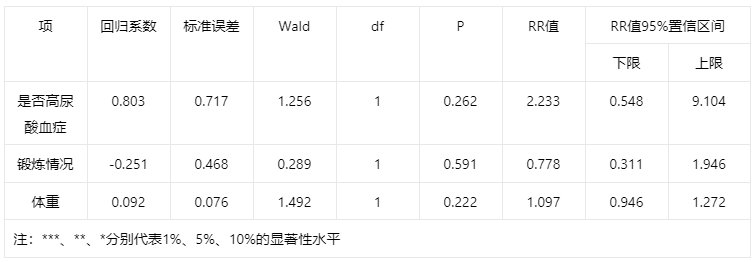

图表说明：
上表展示了模型的参数结果，可用于生成模型公式。包括模型的系数、标准误差、RR值、置信区间等。
● RR值（相对危险度）：试验组累积发病率/对照组累积发病率。 RR值越大，表明效应越大，若 RR 说明暴露因素与疾病之间无关联；若大于1，说明该因素与疾病呈正相关，若小于1，说明该因素与疾病呈负相关。
1、对于连续自变量的RR值无统计学意义。
2、对于哑变量化的0-1分类自变量的RR值意义为：该变量每升高一个单位（即分类水平从0变为1），发生实验组事件的概率是发生对照组事件的RR倍。
分析：
根据系数和RR值进行分析：
系数为正，故患有高尿酸血症的人更易痛风。RR值代表患有高尿酸血症的人痛风概率是未患有的2.233倍。
系数为负，故锻炼情况值越大的人（越积极锻炼的人）更不易痛风。RR值代表每提升一个等级的锻炼情况的人痛风概率是前一个等级锻炼情况的人的0.788倍。
系数为正，故体重越大更易痛风。RR值代表每提升一个kg体重的人痛风概率是前一个kg值的人的1.097倍。

# 7、注意事项

条件逻辑回归对数据要求较为严格，需要格式正确才能分析。
二分类0-1变量Y可以为定量或者定类。
配对编号变量最好按照顺序进行排列（是有序数字）

# 8、模型理论

# 条件逻辑回归的介绍

一般回归分析使用Logit模型研究二元因变量和一组独立（解释）变量之间的关联。然而，在匹配研究中，无条件的逻辑回归是有偏的，模型通常高估了OR值。而条件逻辑回归允许考虑到分层和匹配，通常用于具有特定条件或属性的病例受试者与没有该条件的n个对照受试者相匹配。
一般来说，可能有1至m个病例与1至n个对照组相匹配。然而，最常见的设计是1：1匹配，其次是1：n匹配，其中n从1到5不等。它的主要应用领域是观察性研究，特别是流行病学。

# 条件逻辑回归的计算

多元逻辑回归的模型表达为：
$L o g i t P = β_{1} x_{1} + β_{2} x_{2} + . . . + β_{p} x_{p}$
参数( $b_{j}$ )的估计采用基于条件概率的极大似然法：
首先建立似然函数L和对数似然函数lnL，当似然函数最大时的参数即为参数的最大似然估计值。
设有n对研究、对照对，观察了m个自变量，其配对差数为: $d_{i j} = x_{i} l_{j} - x_{i} 0_{j} (i = 0, 1, 2, . . ., m; j = 0, 1, 2, . . ., m)$ ，如果有研究对象 $y_{i 1}$ 和 $y_{i 0}$ ，则事件发生的条件概率L_i为：
$L_{i} = \frac{1}{1 + e x p (y_{i 1} - y_{i 0})} = \frac{1}{1 + e x p (\sum_{j \in p}^{} b_{j} d_{i j})} (p 为自变量个数)$
设有n个配对组，每个配对组发生概率是 $L_{i}$ 的连续乘积，称为似然函数：
$L = \prod_{i = 1}^{n} L_{i} = \prod_{i = 1}^{n} \frac{1}{1 + e x p (\sum_{j \in p}^{} b_{j} d_{i j})}$

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 王铁兵,邰昌松,汪东篱,苏展,姚兆基,陈志云.深圳结核杆菌感染多因素条件逻辑回归分析[J].疾病监测与控制,2011,5(07):406-407+405.

建议反馈