Bland-Altman法

操作视频

SPSSPRO教程-Bland-Altman法

# 1、作用

Bland-Altman 法是一种可视化进行一致性检验的方法。其原理是一种用 2 种方法结果的差值、均值及 95%一致性(LoA)绘制图形直观的方法，从而得出 2 种方法结果是否具有一致性。

# 2、输入输出描述

输入：代表两种方法的两个定量变量。
输出：Bland-Altman 图以及方法是否具有一致性。

# 3、案例示例

案例：医院有两种检测方法，其中一种是方法 A（传统准确，但是费用高），一种是方法 B（新方法，费用低），需要检测两种检测方法是否具有一致性。

# 4、案例数据

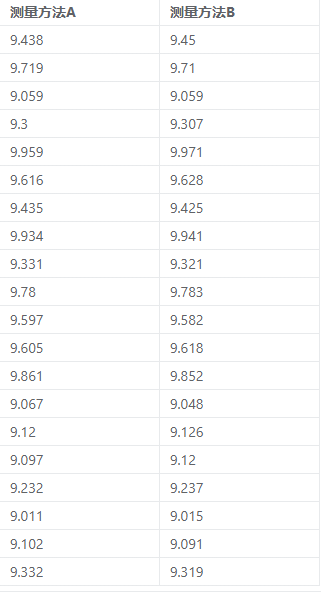
Bland-Altman法案例数据

# 5、案例操作

Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

step4：选择【Bland-Altman 法】；
step5：查看对应的数据数据格式，拖入对应的选项；
step6：选择对应的检验方法，本例为差值法；
step7：进行最大误差区间的设置（指实验中不可超过的最大误差，会反映在 Bland-Altman 图中），本例选择不输入最大误差区间；
step8：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：Bland-Altman 法结果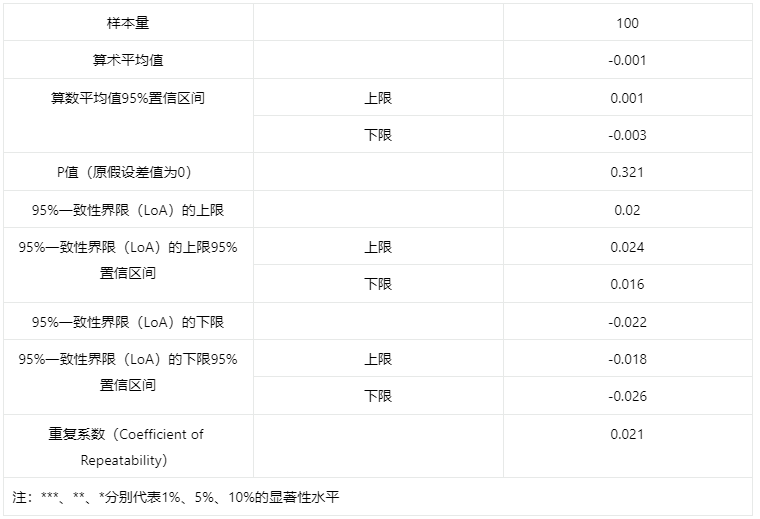

图表说明：
上表展示 Bland-Altman 法的结果，主要是平均值，P 值（用于辅助判断一致性）以及一致性界限(LoA)的值。
分析：
原假设差值为 0 的 P 值为 321，不拒绝原假设，认为差值为零，辅助判断存在一致性。
而 95%一致性界限（LoA）在-0.022 与 0.02 之间，也认为存在一致性。

输出结果 2：Bland-Altman 图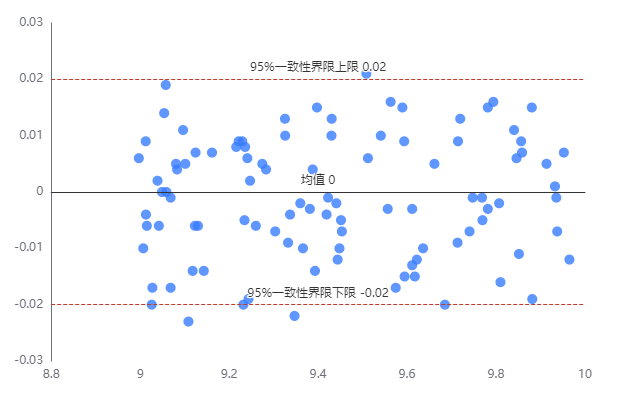

图表说明：
上表展示了 Bland-Altman 图，用于分析一致性情况。点越多在 95% LoA（图中虚线）之内，一致性越好。
智能分析：
从 Bland-Altman 图中可以看出，0.02%（2/100）的点在 95% LoA 之外。
分析：
仅有 0.02%的点在 95% LoA 之外，可以认为一致性良好。

# 7、注意事项

Bland-Altman 法结果的 P 值为配对样本 T 检验的结果。

# 8、模型理论

Bland-Altman 分析最初是由 Bland JM 和 Altman DG 于 1986 年提出的。它的基本思想是计算出两种测量结果的一致性界限（Limits of Agreement）并用图形的方法直观地反映这个一致性界限。最后结合实际得出两种测量方法是否具有一致性的结论。

# 1 一致性界限

在进行两种方法的测定时通常是对同一批受试对象同时进行测量。这两种方法一般不会获得完全相同的结果总是存在着有一定趋势的差异如一种方法的测量结果经常大于（或小于）另一种方法的结果这种差异被称为偏倚（bias）。
偏倚可以用两种方法测定结果的差值的均数 $\overset{―}{d}$ 进行估计 $\overset{―}{d}$ 的变异情况则用差值的标准差 $S_{d}$ 来描述。如果差值的分布服从正态分布则 95％的差值应该位于 $\overset{―}{d} － 1.96 S_{d}$ 和 $\overset{―}{d} ＋ 1.96 S_{d}$ 之间。我们称这个区间为 95％的一致性界限绝大多数差值都位于该区间内。如果两种测量结果的差异位于一致性界限内在临床上是可以接受的则可以认为这两种方法具有较好的一致性这两种方法可以互换使用。如果两种测量方法中没有一种是“金标准”或者不能确定哪种方法一定反映真实值则可以用两种测量结果的平均值作为最终测量结果。
当样本量较小时抽样误差会相对较大，因此还要给出 95％一致性界限的上下限的置信区间。差值均数的标准误 $S E (\overset{―}{d}) = S_{d} / \sqrt{n}$ 一致性界限的上、下限的标准误近似等于 $1.71 S E (\overset{―}{d})$ 则可以分别计算出一致性界限上限的 95％置信区间和下限的 95％置信区间。

# 2 Bland-Altman 图

Bland-Altman 图以图形的方式反映一致性界限。在二维直角坐标中用横轴 x 表示两种方法测量每个对象的平均值纵轴 y 表示两种方法测量每个对象的差值即可得到 Bland-Altman 图。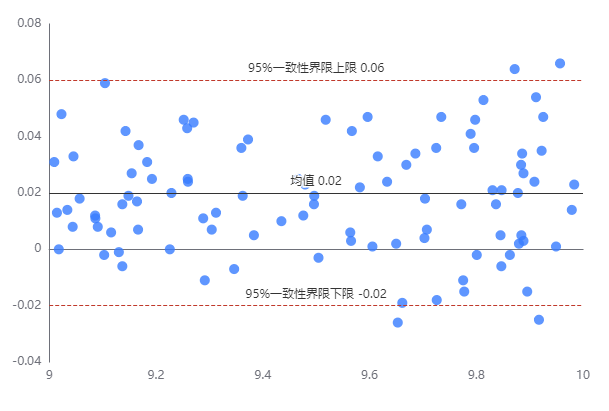

图中上下两条红色虚线代表 95％一致性界限的上下限。中间实线代表差值的均数。还有一根代表差值均数为 0 的实线。两种测量方法的一致程度越高代表差值均数的实线越接近代表差值均数为 0 的实线。
再根据 95％一致性界限外的数据点数和一致性界限内的最大差值以及临床上的可接受程度对待评价的两种方法的一致性做出评价。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 李荣娟, 苏武锦. Bland-Altman 分析法在临床检验方法比较的实例应用和绘图介绍[J]. 国际检验医学杂志, 2013, 34(20):3.
[3] 陈卉. Bland-Altman 分析在临床测量方法一致性评价中的应用[J]. 中国卫生统计, 2007, 24(003):308-309.

建议反馈