Fisher精确检验

操作视频

SPSSPRO教程-Fisher精确检验

# 1、作用

卡方检验主要是比较定类变量与定类变量之间的差异性分析。当样本总量小于 40，或任何格子出现期望频数 T<1，或检验所得的 P 值接近于检验水准 $α$ ，更适合使用 Fisher 精确检验。

# 2、输入输出描述

输入：一个定类变量 X（如班级字段，包括 A、B）与定类变量 Y（如 A 班级 24 名学生与 B 班级 12 名学生的成绩）。
输出：模型输出的检验结果，如 A 与 B 班级的学生成绩存在/不存在显著性差异。

# 3、案例示例

从某高中学随机抽取两班级（总样本量为 36，小于 40），调查考试成绩是否有显著差异。

# 4、案例数据

Fisher 精确检验案例数据

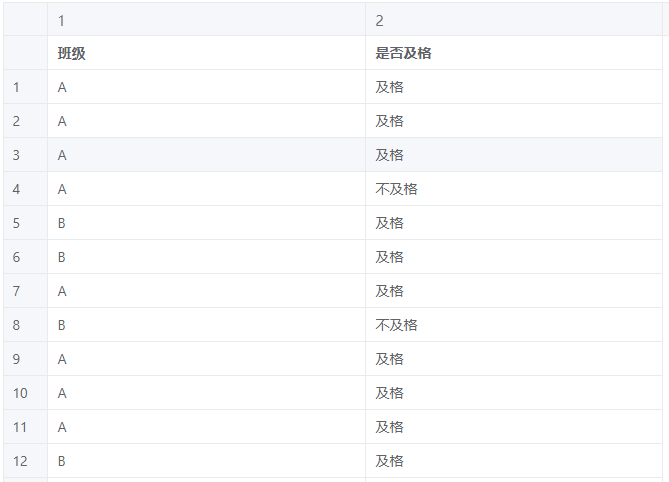
# 5、案例操作

Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

step4：选择【Fisher 精确检验】；
step5：查看对应的数据数据格式，按要求输入【Fisher 精确检验】数据;
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：Fisher 精确检验结果

题目	名称	班级		合计	p 值
		A	B
成绩	不及格	2	4	6	0.149
	及格	22	8	30
合计		24	12	36

注：*、**、***分别代表 1%、5%、10%的显著性水平

图表说明：上表展示了 Fisher 精确检验的结果，包括数据的频数、显著性 P 值。
● 若 p<0.05，呈现显著性，拒绝原假设，则说明分类变量 X 与分类变量 Y 之间存在显著性差异。
● 若 p>=0.05，不呈现显著性，接受原假设，则说明分类变量 X 与分类变量 Y 之间不存在显著性差异。
分析：Fisher 精确检验分析的结果显示，显著性 P 值为 0.149，水平上不呈现显著性，不能拒绝原假设，因此班级和成绩数据不存在显著性差异。

输出结果 2：交叉列联表热力图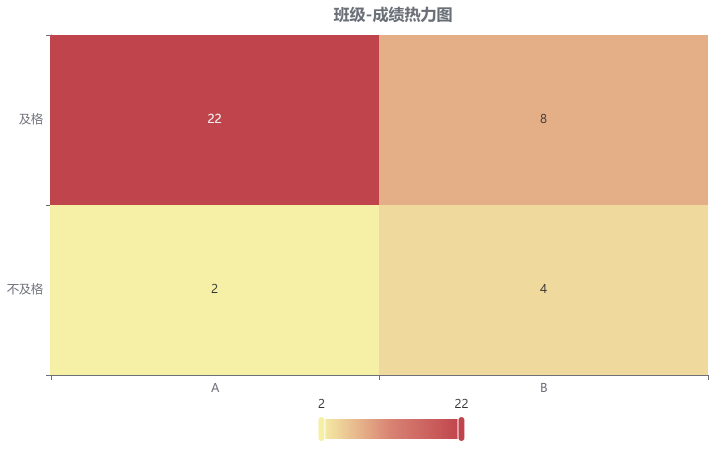

图表说明：上图展示了热力图的形式展示了交叉列联表的值，主要通过颜色深浅去表示值的大小。

# 7、注意事项

一般优先考虑皮尔森卡方检验，当 n ≥40，T(理论频数) ≥ 5，用 Pearson 统计量
当 n≥40 时，如果某个格子出现 1≤ T ≤5，则需作叶氏连续性校正
当 n<40，或任何格子出现 T<1，或检验所得的 P 值接近于检验水准 $α$ ，采用 Fisher 精确检验
Fisher 精确检验存在阶乘运算，不适用于大样本情况

# 8、模型理论

1.简介

Fisher 精确检验没有统计量，更没有繁琐的统计量的表格，它算出来的就是 p 值，但是它在大样本情况下手算几乎是不可能的，因为它涉及到阶乘运算。

2.原理

同是固定边际频数不变，与 Pearson 的思想不同，Fisher 考虑的是超几何分布：固定边际频数不变后，每次抽样就相当于从边际频数中抽取数字填进四格表中，从而得到样本的情形服从超几何分布。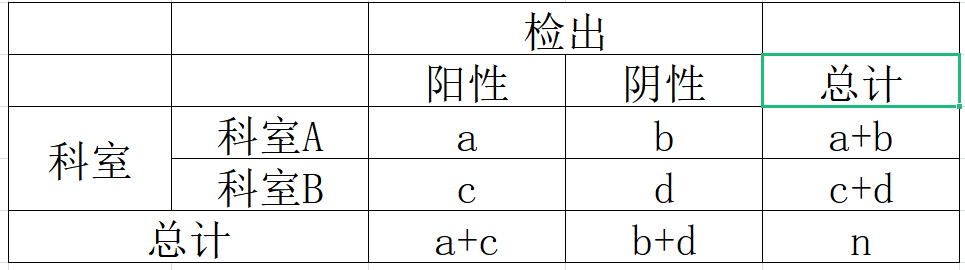

例如上表 A,B 两个科室检查癌症的情况的例子。

第一个分式表示的是从个样本中抽取个患者，其中个是科室 A 检测、 $c$ 个是科室 B 检测的概率。
第二个分式表示的是从个样本中抽取个患者，其中个是科室 A 检测、个是科室 B 检测的概率。
这里比较的是正常人的科室 A，B 比和患者的科室 A，B 比的差异，由于总频数和边际频数都是固定的，因此它们两个计算出来的结果相等。
Fisher 给出的这样的概率就是值，是精确的。但不能只计算当前样本情形的值，因为假设检验的值都是累积概率值，还需要计算其它情形的概率的和。

3.计算过程

为了简化起见，我把样本量设得很小，倘若实际抽样得到的结果是这样的：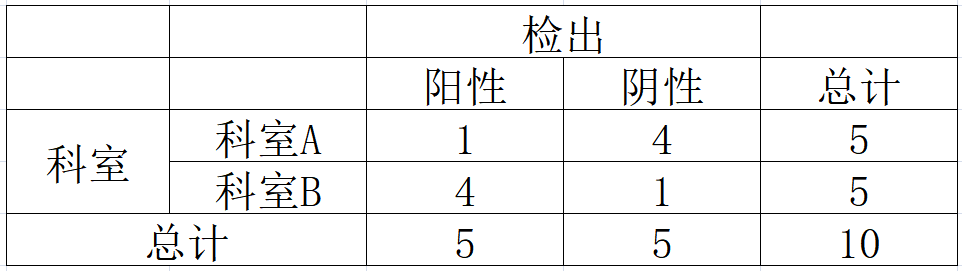

代入公式得到 $p_{1} = \frac{5! 5! 5! 5!}{1! 4! 1! 4! 10!} = 0.09920635$ 。那么总样本数和边际数不变的情况下，我们变动四格表中的数字，同上可以计算出其他 5 种情形，分别为 $p_{2} = 0.00396825$ ， $p_{3} = 0.3968254$ ， $p_{4} = 0.3968254$ ， $p_{5} = 0.09920635$ ， $p_{6} = 0.00396825$ 。

4.分析

如果是双侧检验，我们的值等于两段的和：增加的那段和减少的那段中的小于样本情形的的和。在这个例子中双侧检验的，它检验的意义是需要考虑对称的情况。
如果单侧检验，只需计算样本所在那一段中当前情形以及比它更极端的情形的的和。在这个例子中，单侧检验的。我们已经知道患病人群中，科室 A 比科室 B 更多，因此这个例子选择单侧检验更合适，然而在显著性水平为的情况下仍不能拒绝原假设。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]方积乾.生物医学研究的统计方法[M].高等教育出版社:北京,2007:138-139.
[3]Greenwood, P. (1996).A Guide to Chi-Squared Testing (Wiley Series in Probability and Statistics)1st Edition. Wiley Interscience.

建议反馈