比例风险回归(COX回归)

# 1、作用

COX 回归模型，又称“比例风险回归模型。该模型以最终结局和生存时间为因变量，同时分析众多因素对生存时间的影响，目前在医疗，金融和市场研究等专业领域中广泛使用。如医学研究中，药物 X 的使用是否增加或减少病人的存活时间等等。

# 2、输入输出描述

输入：时间变量，状态变量，自变量 X 至为少一项或以上的变量，如有分层或者绘图需求则输入对应变量。
输出：不同因素对生存期的影响情况。

# 3、案例示例

案例：根据罪犯第一次被逮捕后的周数和人种、是否已婚等变量，分析不同因素对罪犯是否再次犯罪以及之后再犯时间的影响情况。

# 4、案例数据

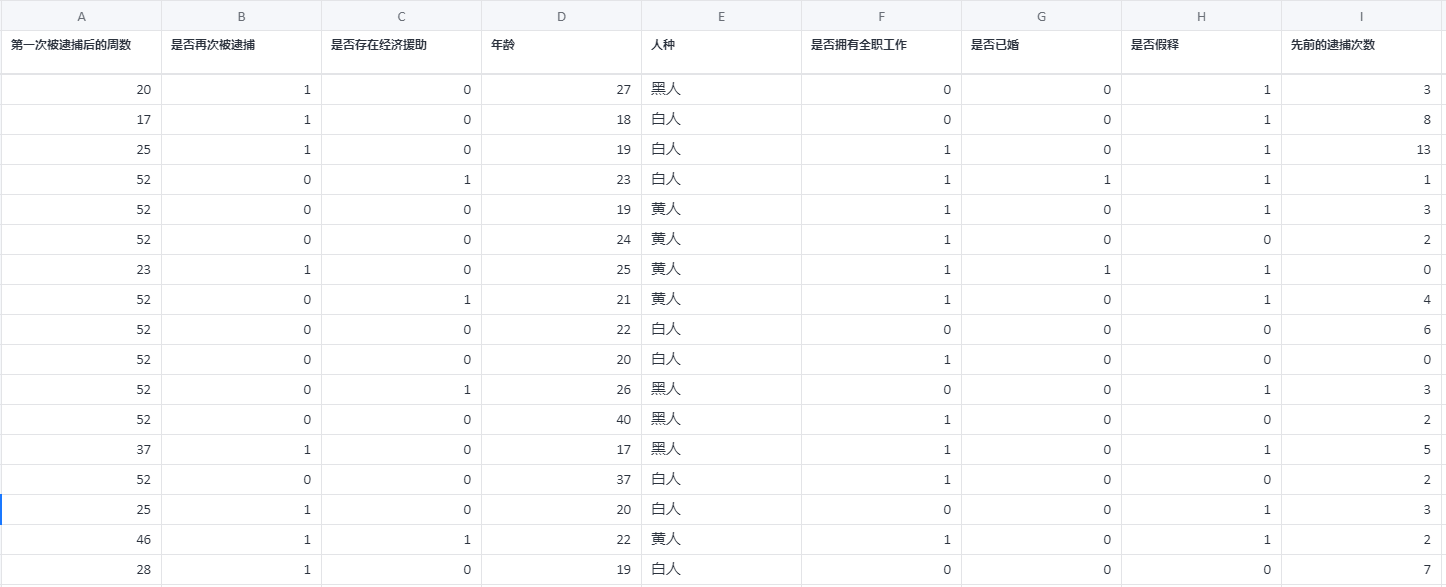
# 5、案例操作

Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；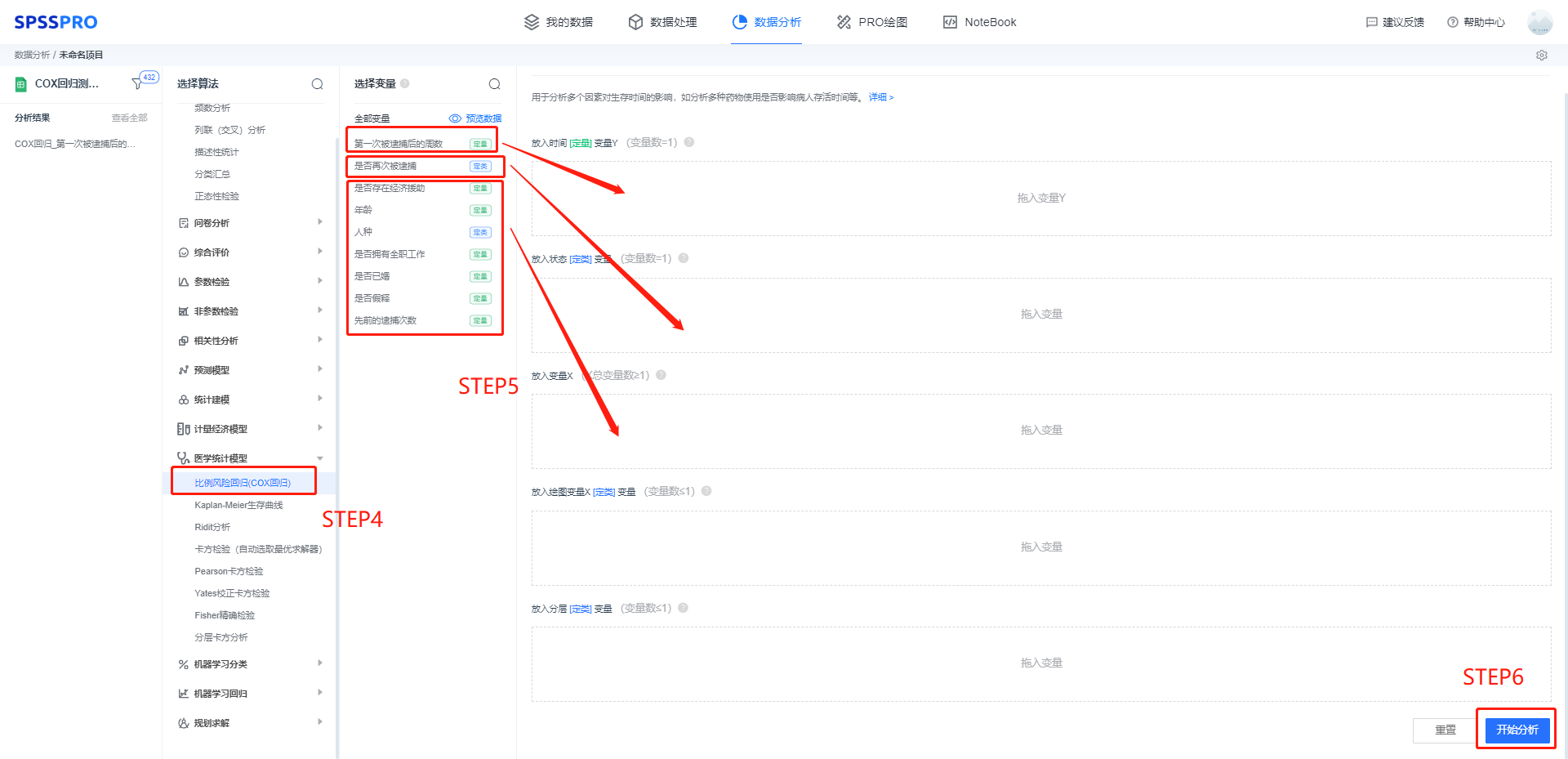

step4：选择【比例风险回归(COX 回归)】；
step5：查看对应的数据数据格式，拖入对应的选项；
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：Ominbus 全局性检验

图表说明：上表展示了样本 Ominbus 全局性检验的结果，包括-2 倍对数极大似然值、卡方值等，用于检验模型中所有变量的回归系数是否全为零。-2 倍对数极大似然值用于检验模型的拟合情况，其值越小，表示模型拟合的越好。
分析：Ominbus 全局性检验的显著性 P 值为 0.000***，水平上呈现显著性，拒绝原假设，因此数据至少存在一个变量的风险比率不为零,模型有效。

输出结果 2：回归系数汇总情况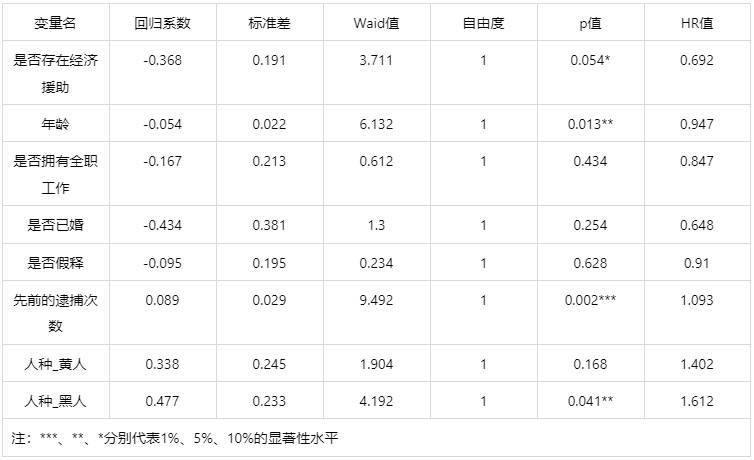

图表说明：
上表展示模型的回归系数的大小，标准差，Waid 值，P 值和 HR 值。
● P 值用于判断是否显著影响，回归系数的大小与正负判断是正向还是负向影响。
● Wald 是一个卡方值，用于对回归系数进行检验，考察回归系数是否等于 0。
● HR 值为风险函数值比值，简称风险比，其意义如下：
HR 值大于 1，提示是阳性事件发生的促进因素；
HR 值小于 1，提示是阳性事件发生的阻碍因素；
HR 值等于 1，提示对阳性事件的发生无影响。
分析：年龄和先前的逮捕次数对是否累犯有显著性影响。其中年龄是被再次逮捕的阻碍因素（年级越大越不容易累犯），先前的逮捕次数和是否黑人（人种的哑变量结果）是促进因素（先前被逮捕的次数越多或者是黑人越容易累犯）。

输出结果 3：生存曲线图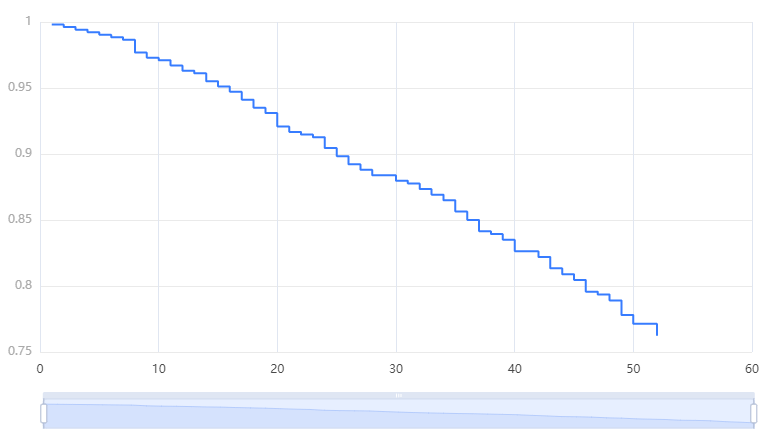

图表说明：上图展示了样本总体随着时间的推移的生存情况。其中横轴是时间，纵轴是累计生存率。

# 7、注意事项

• 状态变量只能是二分类 0、1 变量，并且 1 代表是事件发生（如死亡/阳性等）；
• PH 假定可以通过看各组的生存曲线是否交叉简单判断，复杂判断可以使用 Schoenfeld 残差图、累计风险函数法和 Score 残差图等判断。
• 如果某个分类性质的混杂因素不满足风险比例假设，可以将其作为分层变量进行分层分析，用以控制混杂（该变量将作为分层项，没有结果）；
• 绘图变量可以对比不同类型的生存曲线情况（将绘制按照该变量分类的多条生存曲线）；

# 8、模型理论

Cox 比例风险回归模型见下式：

在上式中，X1、X2、⋯、Xp 为与生存时间可能有关的自变量（即影响因素），其中的自变量或影响因素可能是定量的或定性的，在整个观察期内不随时间的变化而变化；h(t)为具有自变量 X1、X2、⋯、Xp 的个体在 t 时刻的风险函数；h0(t)为所有自变量为 0 时 t 时刻的风险函数，称为基准风险函数（baseline hazard function），是未知的；β1、β2、⋯、βp 为各自变量的偏回归系数，是一组未知的参数，需要根据实际的数据来估计。
Cox 模型不直接考察生存函数 S(t)与自变量的关系，而是利用生存函数 S(t)与风险函数 h(t)的关系，将风险函数 h(t)作为因变量，间接反映自变量与生存函数 S(t)的关系。该模型右侧可分为两个部分：一部分为 h0(t)，它没有明确的定义，分布无明确的假定，为非参数部分；另一部分是以 p 个自变量的线性组合为指数的指数函数，具有参数模型形式，其中回归系数反映自变量的效应，可通过样本实际观测值来估计。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 严若华,李卫.Cox 回归模型比例风险假定的检验方法研究[J].中国卫生统计,2016,33(02):345-349.
[3]姚婷婷,刘媛媛,李长平,胡良平.生存资料回归模型分析——生存资料 Cox 比例风险回归模型分析[J].四川精神卫生,2020,33(01):27-32.