分层卡方分析

操作视频

# 1、作用

分层卡方是在卡方检验基础上，进一步考虑分层项的干扰（混杂因素）。比如想要调查某一地区接种疫苗（X) 对感染病毒 (Y) 的影响，由此来判断疫苗的有效性；但考虑到男性、女性体质的不同，疫苗可能会造成不一样的抵抗病毒能力，因此将性别 (Z) 作为混杂因素来进行分析。SPSSPRO 仅支持 22k 表格的数据结构（即 X 和 Y 均为有 2 个分类水平，k 是指混杂因素 Z 的 k 个水平）。

# 2、输入输出描述

输入：一个定类变量 X 与定类变量 Y，一个分层项（混杂变量 Z）
输出：检验混杂变量 Z 是否具有意义；混杂变量 Z 不同分组的卡方检验结果以及整体卡方检验结果。

# 3、案例示例

案例：某地区有一项关于是否接种疫苗（X）对于感染病毒 (Y) 风险的影响，将性别 (Z) 作为混杂因素来建立分层卡方检验来进行分析。

# 4、案例数据

分层卡方分析案例数据

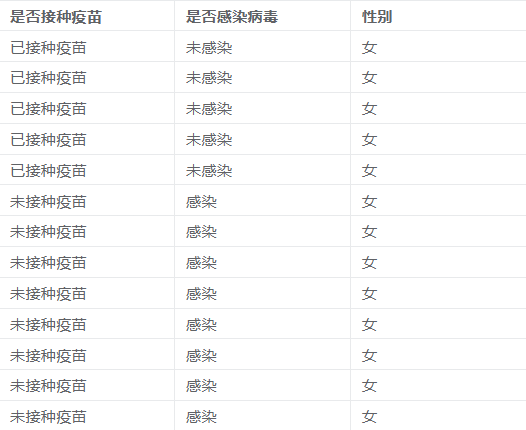
# 5、案例操作

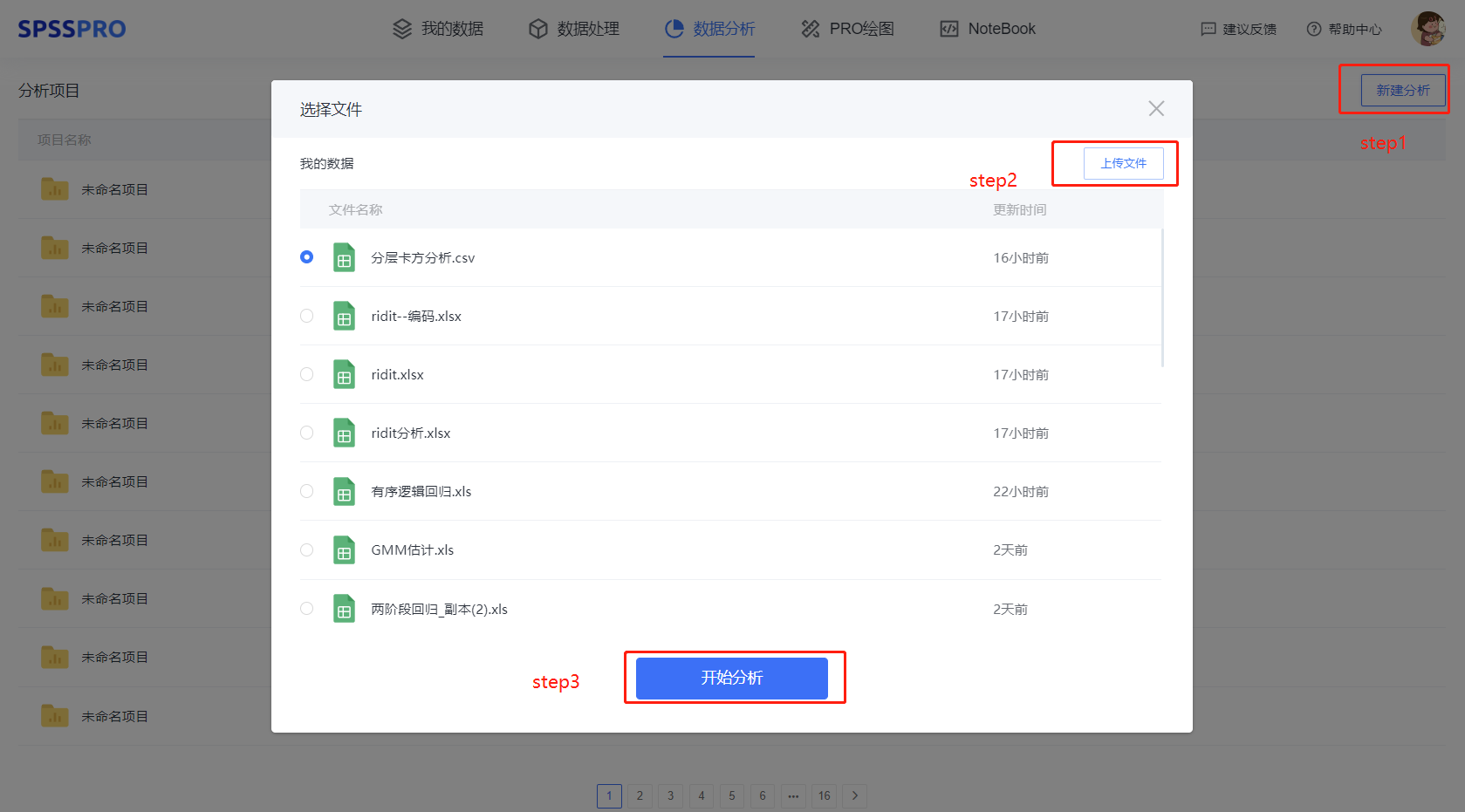
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；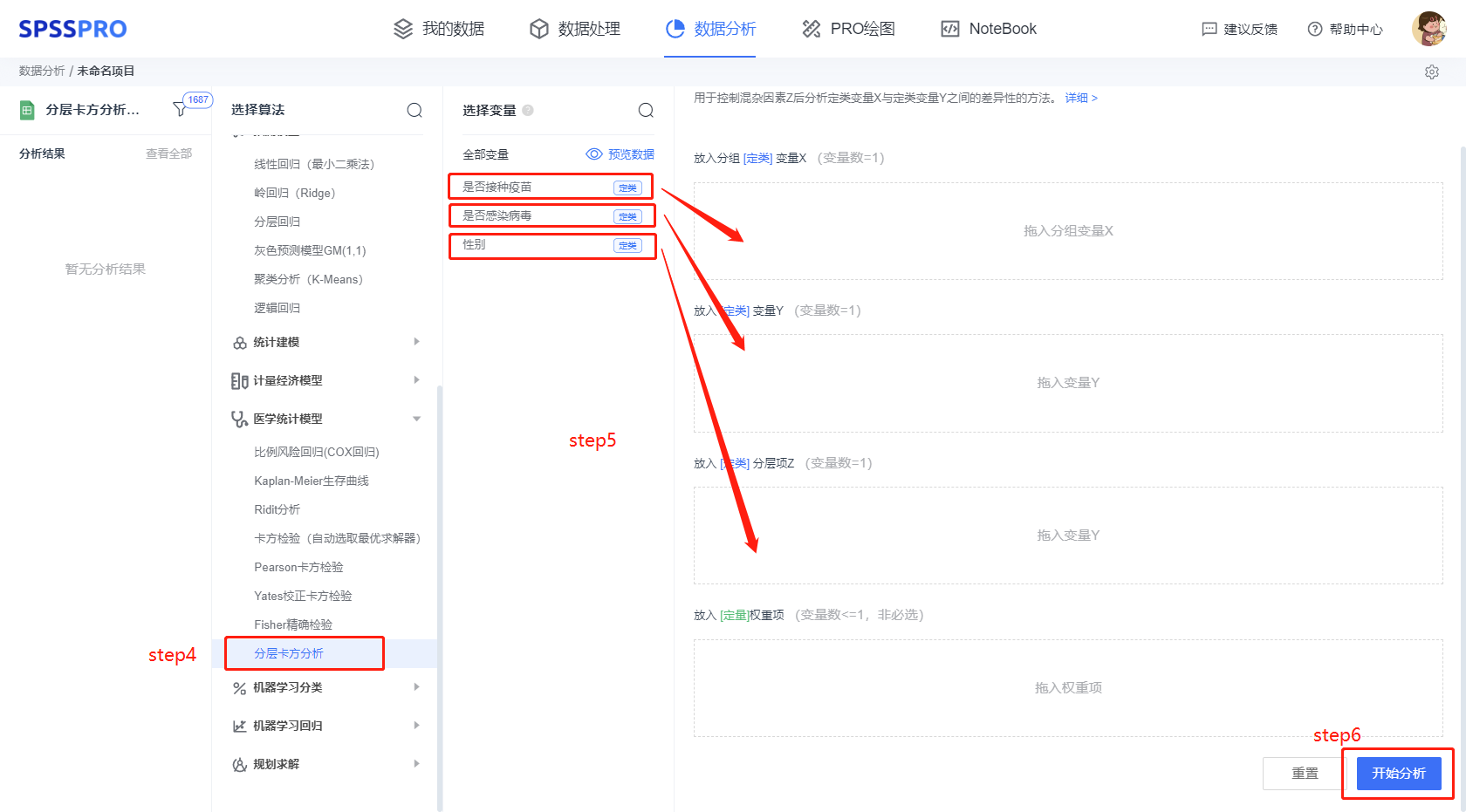

step4：选择【分层卡方分析】；
step5：查看对应的数据数据格式，拖入对应的选项；
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：数据汇总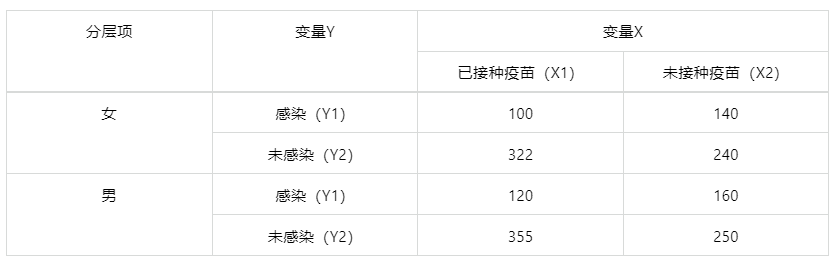

图表说明：上表以分层列联表的形式对各变量数据进行汇总。

输出结果 2：比值比齐性检验结果

图表说明：比值比齐性检验的显著性 P 值为 0.970，不存在显著性，说明混杂因素各分类之间同质，并不存在混杂作用，并不需要分别报告混杂因素各分类对应的值（比如 OR 值），而需要整体计算 OR 值，可关注输出结果 4 的 CMH 条件独立性检验结果。

输出结果 3：分层卡方分析结果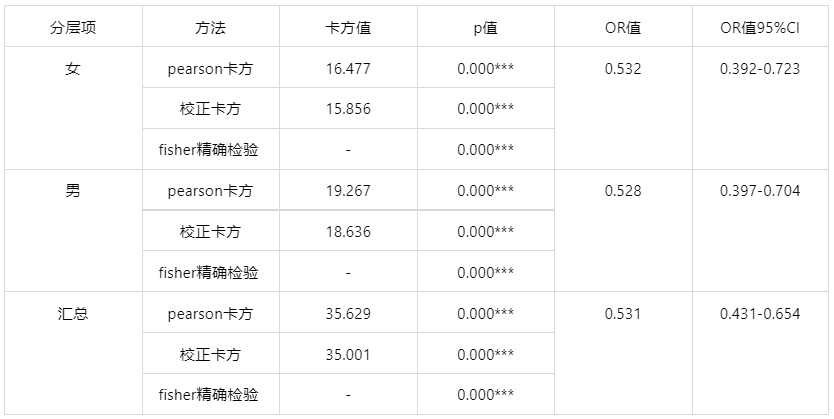

图表说明：
对于分层项-女，建议使用 Pearson 卡方检验，显著性 P 值为 0.000***，水平上呈现显著性，拒绝原假设，因此是否感染病毒和是否接种疫苗数据存在显著性差异。
对于分层项-男，建议使用 Pearson 卡方检验，显著性 P 值为 0.000***，水平上呈现显著性，拒绝原假设，因此是否感染病毒和是否接种疫苗数据存在显著性差异。
对于分层项-汇总，建议使用 Pearson 卡方检验，显著性 P 值为 0.000***，水平上呈现显著性，拒绝原假设，因此是否感染病毒和是否接种疫苗数据存在显著性差异。
但是，由于输出结果 2 的证明了混杂因素各分类之间同质，并不存在混杂作用，所以不需要过多地关注该结果。

输出结果 4：CMH 条件独立性检验

图表说明： OR 值（Odds Ratio 优势比）：
● 若 OR>1，是指分类变量 X1 导致 Y1 发生的概率比 X2 导致 Y1 发生的概率高了（OR-1)%。
● 若 OR<1，是指分类变量 X1 导致 Y1 发生的概率比 X2 导致 Y1 发生的概率低了（1-OR)%。
● 若 OR=1，是指分类变量 X1 导致 Y1 发生的概率与 X2 导致 Y1 发生的概率没有差别。 CMH 条件独立性检验的显著性 P 值为 0.000***，存在显著性，说明去除混杂因素影响后，是否感染病毒和是否接种疫苗之间存在显著差异。并且 OR 值为 1.886，可以认为分类变量 X1（已接种疫苗）导致 Y1（感染病毒）发生的概率比 X2（未接种疫苗）导致 Y1（感染病毒）发生的概率低了 47%，这说明接种疫苗是有用的，能减少感染病毒的概率。

# 7、注意事项

SPSSPRO 仅支持 22k 表格的数据结构（即 X 和 Y 均为有 2 个分类水平，k 是指混杂因素 Z 的 k 个水平）。

# 8、模型理论

分层卡方检验，也称为 CMH 检验，它主要用于分层或匹配分类数据的分析，该方法的运算通常基于 2×2×K 的列联表(K 为类别数或分层数)，通过用分层的思想对混杂因素进行调整，把研究对象分解成不同层次，按各层对象来进行行变量与列变量的独立性研究，以消除由于资料内部的不均一性所造成的偏倚，使资料分析的结果能够更正确地反映所研究变量之间的相关关系，可在去除阶层因素下，更准确地对行列变量的独立性进行研究。
通常情况下，首先查看‘比值比齐性检验’，如果其呈现出显著性（_p _值小于 0.05），则说明具有混杂因素，即需要考虑分层项，即分别查看不同分层项下的数据结果（即输出结果 3）。反之如果没有通过‘比值比齐性检验’，即说明没有混杂因素不需要考虑分层项，报告整体的结果即可（即输出结果 4）。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]周林. 分层卡方检验在笔迹实验研究中的应用[J]. 广东公安科技,2021,29(1):21-24.

建议反馈