配对卡方检验
# 1、作用
卡方检验(Pearson卡方检验)主要是比较定类变量与定类变量之间的差异性分析。配对卡方检验是对同一样本分别用 A 和 B 两种方法处理,或是对样本前后测量,比较其差性异。
# 2、输入输出描述
输入:一个定类变量 X1 与定类变量 X2 。
输出:模型检验的结果,如方法A和方法B检测结果存在/不存在显著性差异。
# 3、案例示例
为调查治疗方法对抗体的影响,比较两种治疗方法的检测结果是否有差异。
# 4、案例数据
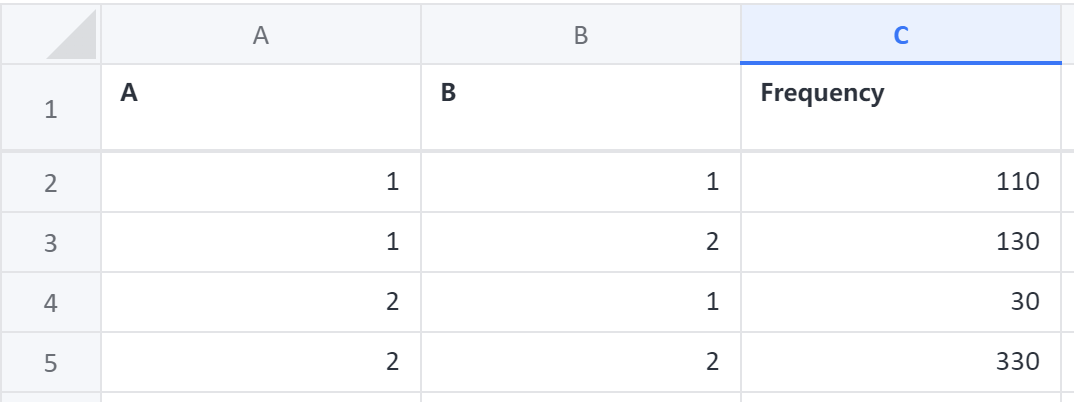
# 5、案例操作
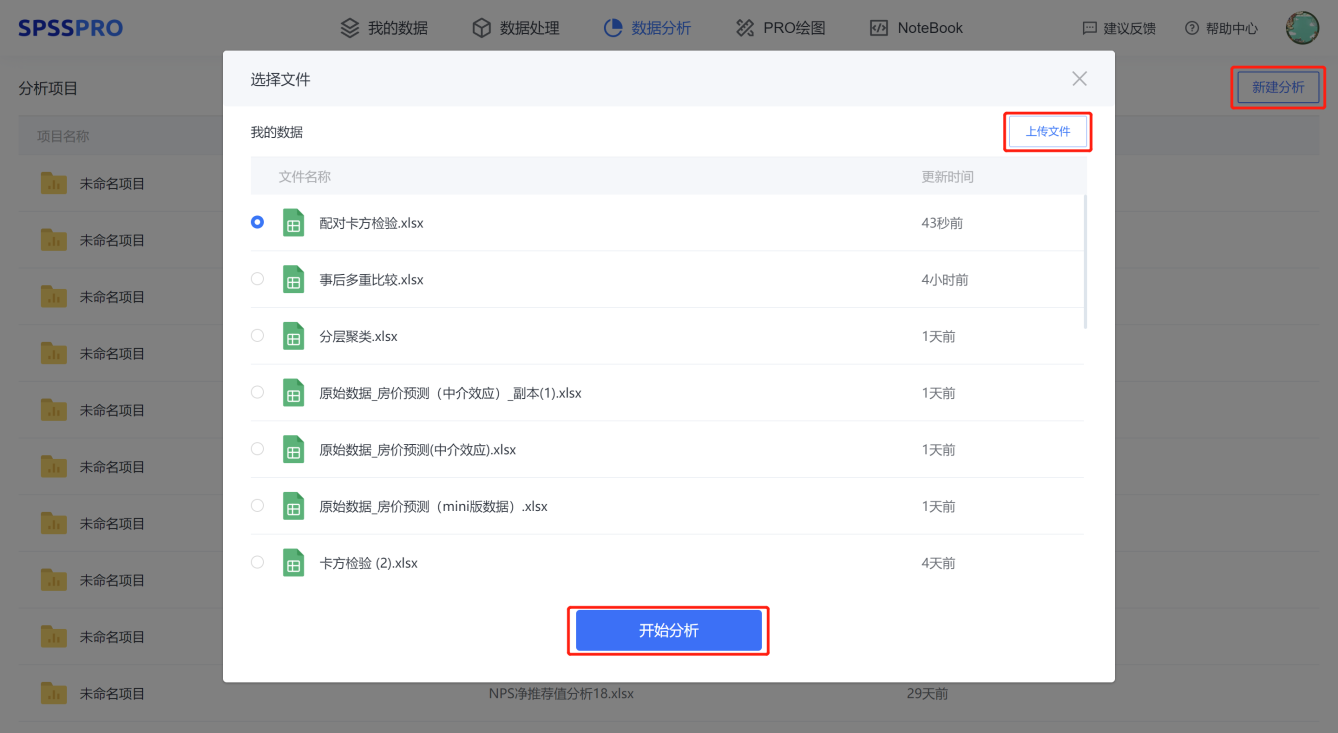
Step1:新建分析;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;
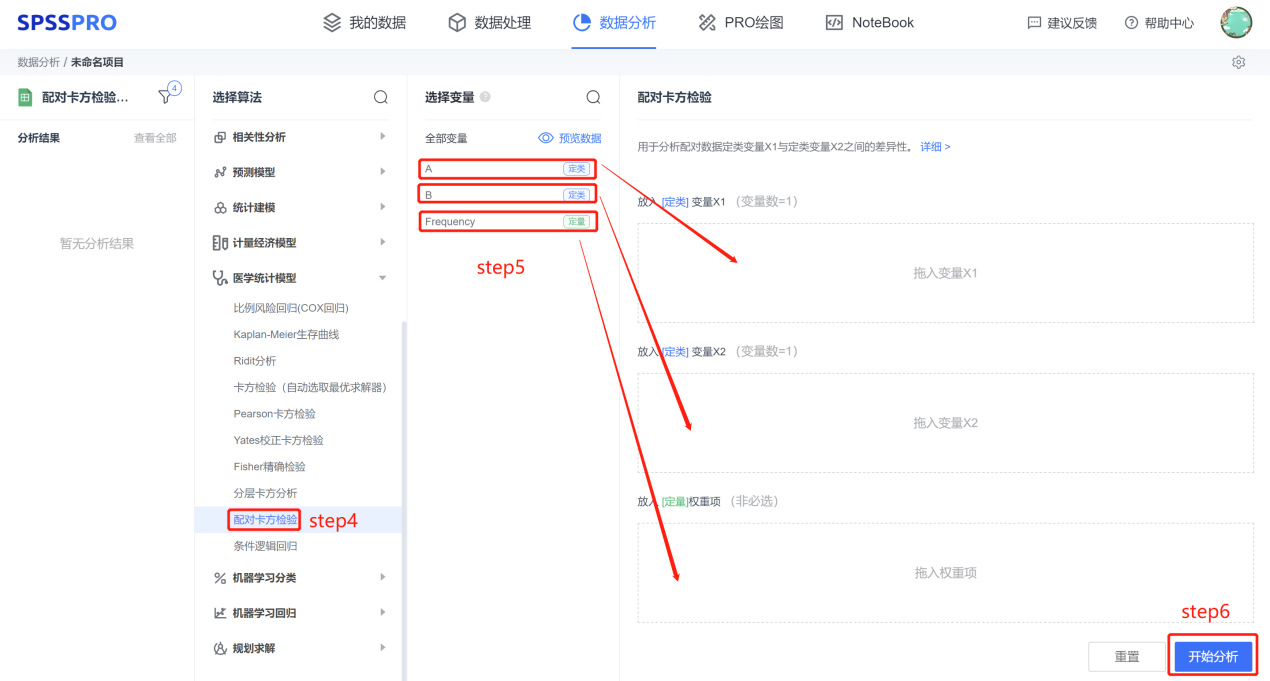
step4:选择【配对卡方检验】;
step5:查看对应的数据数据格式,【配对卡方检验】要求拖入数据为分组定类变量X1,定类变量X2,定量权重项;
step6:点击【开始分析】,完成全部操作。
# 6、输出结果分析
输出结果1:Pearson卡方检验结果
| 配对 | 名称 | A | 合计 | 卡方值 | p值 | |
|---|---|---|---|---|---|---|
| 1.0 | 2.0 | |||||
| B | 1.0 | 110 | 30 | 140 | 61.256 | 0.000*** |
| 2.0 | 130 | 330 | 460 | |||
| 合计 | 240 | 360 | 600 |
图表说明:上表展示了配对卡方检验的结果,包括数据的频数、显著性P值。配对卡方如果是2×2列联表结构时则采用McNemar检验,并当2×2列联表中b+c≤40时,得到的是连续性校正的McNemar检验;如果为n×n(n>2)列联表结构时则采用Bowker检验。
● 若p<0.05,呈现显著性,拒绝原假设,则说明分类变量X1与分类变量X2之间存在显著性差异。
● 若p>=0.05,呈现显著性,拒绝原假设,则说明分类变量X1与分类变量X2之间不存在显著性差异。
分析:配对卡方检验的结果显示,显著性P值为0.000***,水平上呈现显著性,拒绝原假设,因此A和B数据存在显著性差异。
输出结果2:交叉列联表热力图
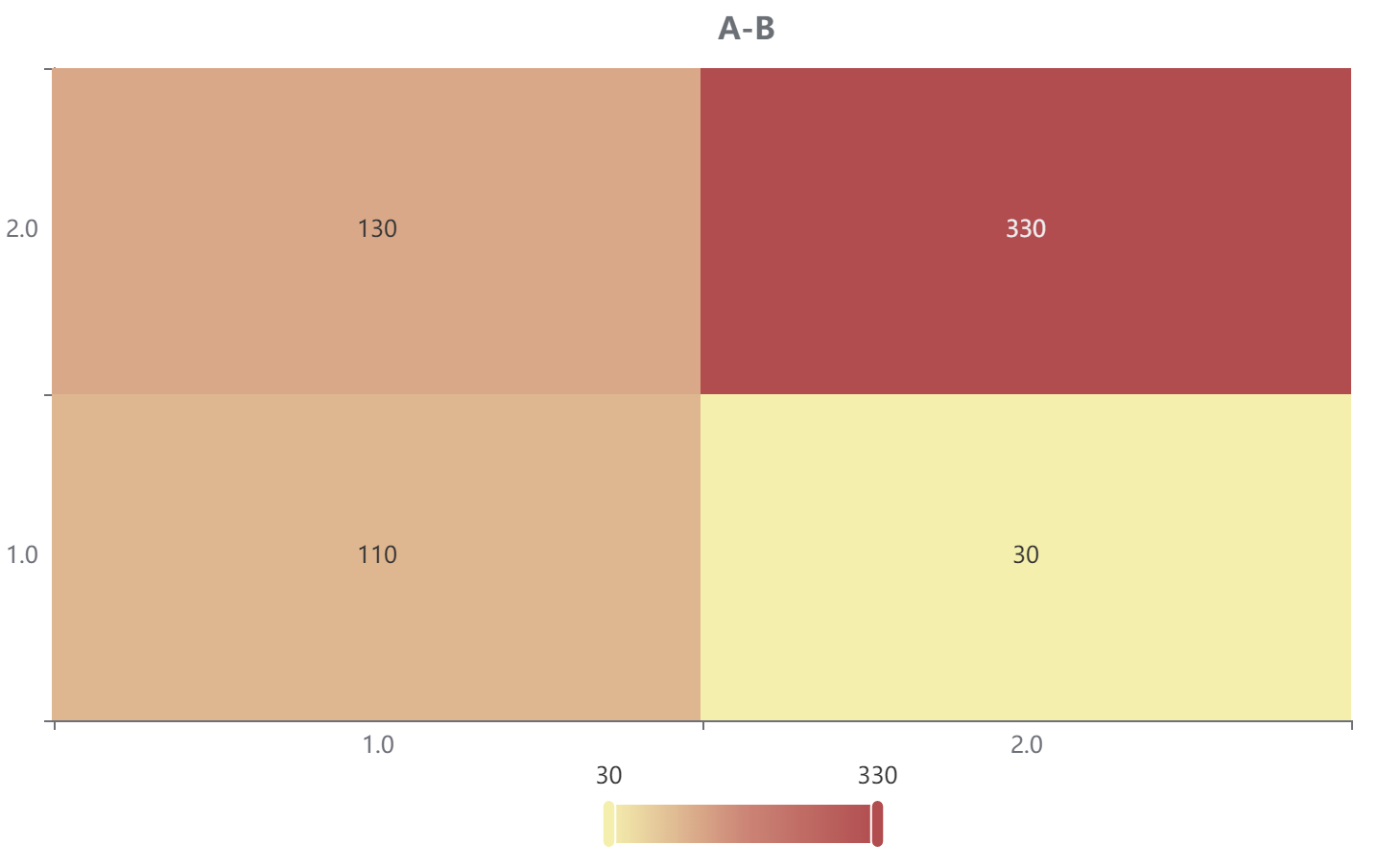
图表说明:上图展示了热力图的形式展示了交叉列联表的值,主要通过颜色深浅去表示值的大小。
# 7、注意事项
- 适用于比较两组的差异
- 需要满足:两个变量 X1, X2 的值(如阳性/阴性)为二分类且两类互斥;
- 变量 X1, X2 (如方法A,方法B)应包含2类且相关,若变量为3个及以上,可用Cochran's Q检验。
# 8、模型理论
# 1.介绍
配对设计的特点是对同一样本分别用 A 和 B 两种方法处理,或是对样本前后测量,观察其水平分布的差异或一致性。若采用配对设计,结局指标为计数资料时,则需要采用配对设计卡方检验。检验方法包括四个表(2x2)卡方检验(McNemar)和多个列联表(KxK)卡方检验(McNemar-Bowker)。这两种方法用的都是McNemar检验。
# 2.举例
例如调查购物广告对消费者购买情况的影响。该项目共招募了50名消费者,让他们观看购物广告。想要比较消费者们在观看广告前和观看广告后购买情况是否有差异。该数据整理成2*2的四表格(其中1编码为购买,2编码为不购买,故第一行表示观看广告前后都购买有21人)
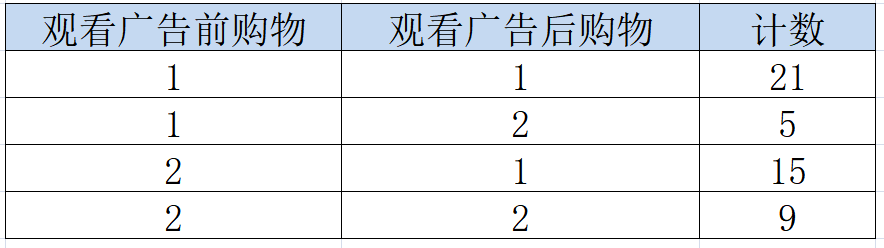
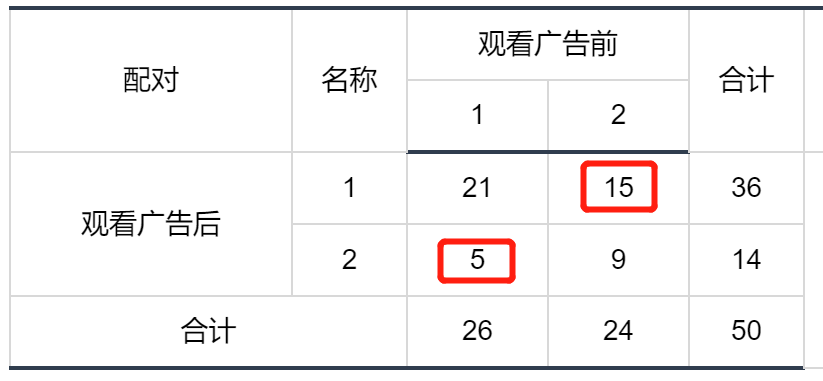
该案例主要分析观看广告前购物比例(26/50=52%)与观看广告后购物比例(36/50=72%)之间是否有差异,本质上就是考察红框中的数字是否相等。
# 3.结果分析
- 卡方检验结果:结果中P=0.025**,因此说明观看广告前后购买情况存在着统计学差异。
- 分析统计结果:分别是观看广告前、后购买的情况,由表中结果可知,观看广告前购买的人数构成比为26/50=52%,观看广告后有购买的人数构成比达到36/50=72%。
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
