Kaplan-Meier生存曲线
# 1、作用
Kaplan-Meier 曲线又称生存曲线，是一种生存分析的常用方法，主要分析单一因素对生存期的影响。
# 2、输入输出描述
输入：时间变量，状态变量，待分析自变量 X。
输出：单一因素对生存期的影响情况。
# 3、案例示例
案例：医院需要研究一种新药的疗效情况，使用 Kaplan-Meier 曲线得到是否使用新药对患者总生存时间的影响。
# 4、案例数据
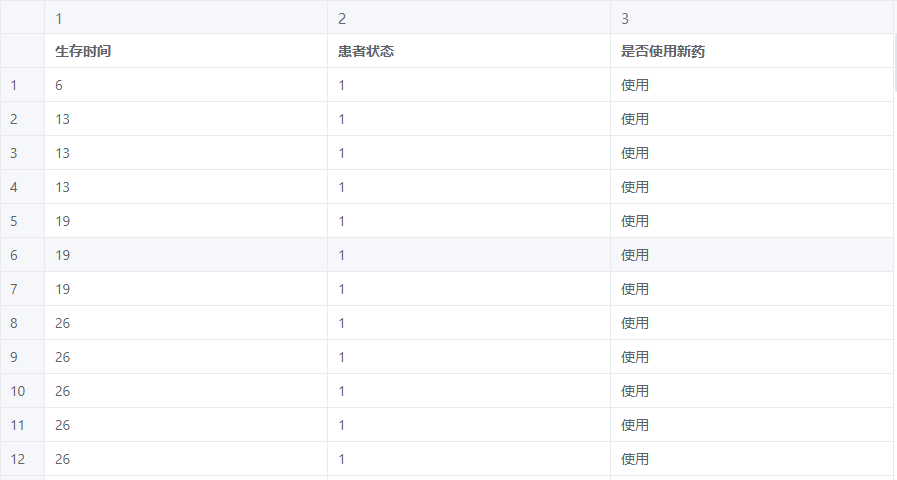
# 5、案例操作
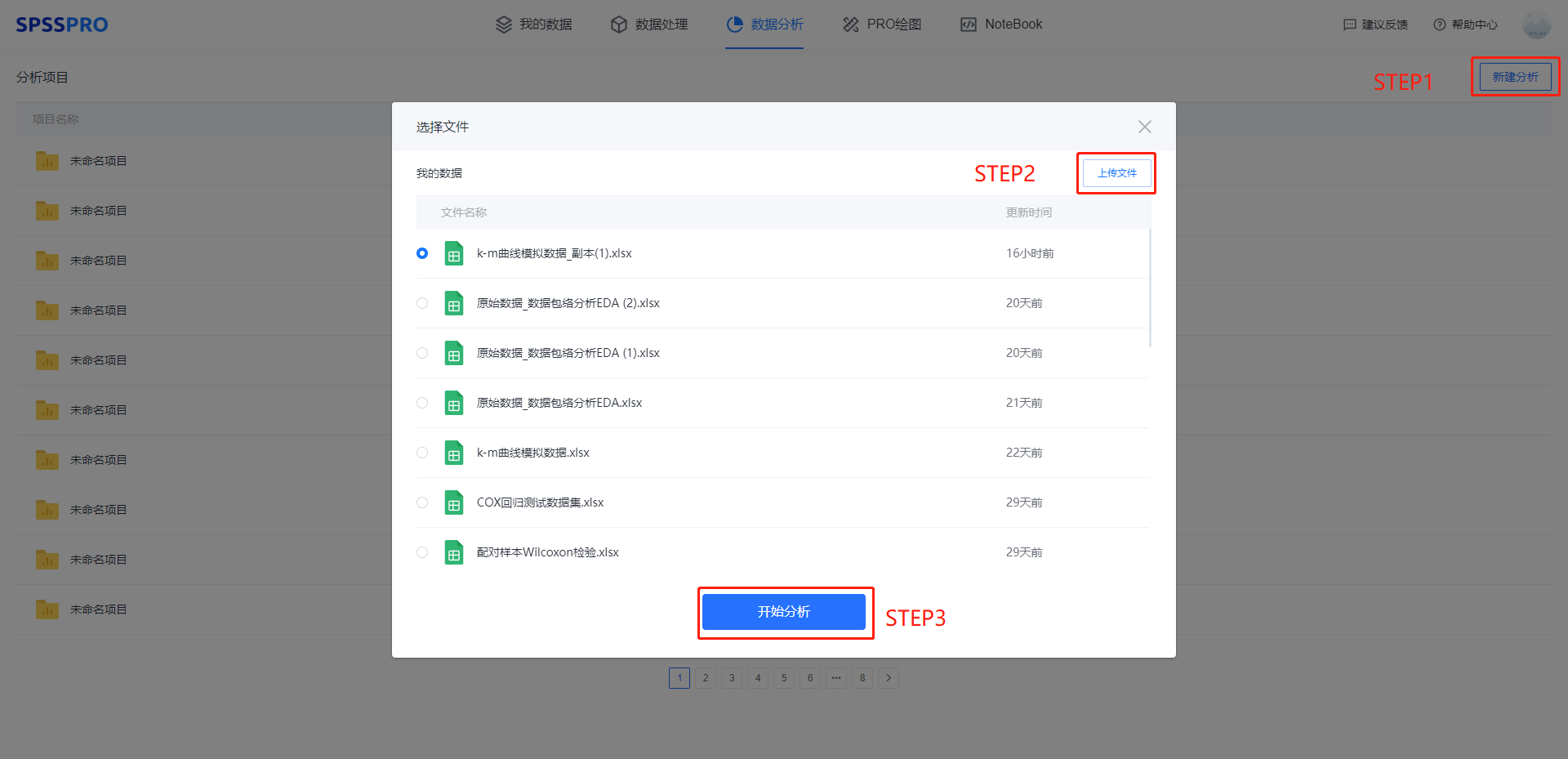
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；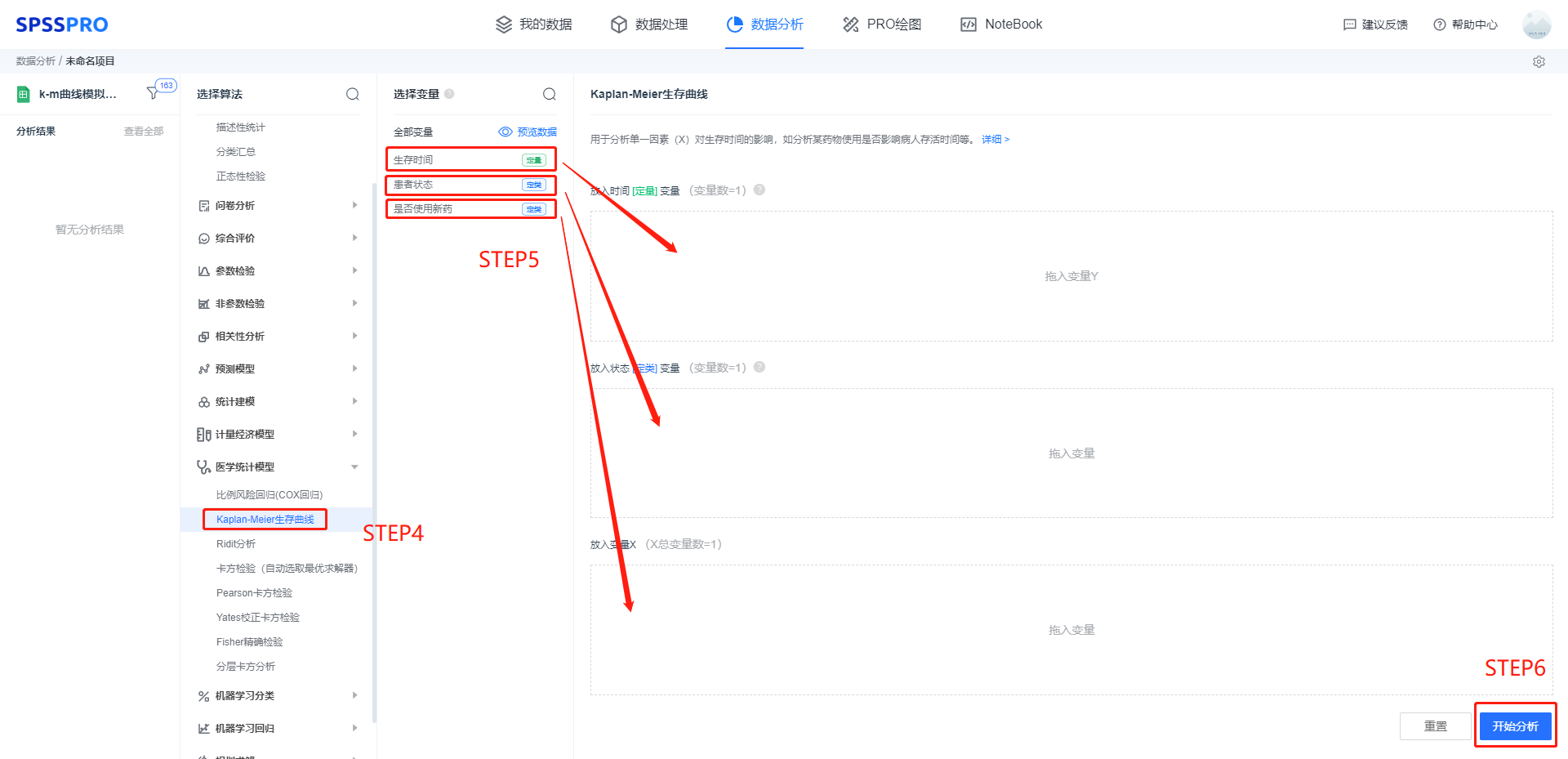
step4：选择【Kaplan-Meier 生存曲线】；
step5：查看对应的数据数据格式，拖入对应的选项；
step6：点击【开始分析】，完成全部操作。
# 6、输出结果分析
输出结果 1：模型数据摘要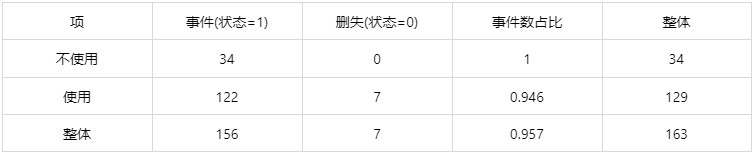
图表说明：
上表展示了样本的事件数（状态=1）/删失数（状态=0）以及事件数占比的情况。
输出结果 2：生存情况的均值和中位数
| 是否使用 | 均值 | 中位数 | ||||||
|---|---|---|---|---|---|---|---|---|
| 估计 | 标准误 | 95%置信区间 | 估计 | 标准误 | 95%置信区间 | |||
| 下限 | 上限 | 下限 | 上限 | |||||
| 不使用 | 25.706 | 2.257 | 21.282 | 30.13 | 26 | 1.531 | 19 | 29 |
| 使用 | 56.628 | 0.954 | 54.758 | 58.498 | 58 | 1.02 | 56 | 60 |
| 整体 | 50.134 | 1.331 | 47.526 | 52.742 | 56 | 1.02 | 53 | 58 |
图表说明：
上表展示了各项均值和中位数的估计值和标准误差以及其 95%的置信区间，一般以中位数为准。
分析：
使用新药的中位生存时间是 58 周，而不使用新药是 26 周。可以认为新药的使用明显带来好处，使得生存时间有较大延长。
输出结果 3：生存状态差异检验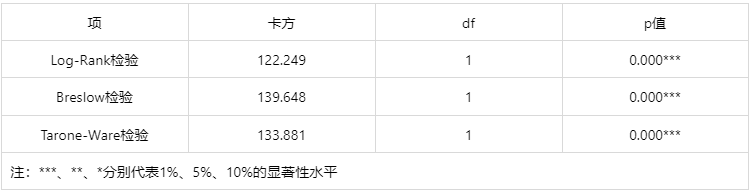
图表说明：
上表展示了三种卡方检验方法的结果，用以检验生存函数在两组样本上是否存在 统计学差异（一般判断标准为 P 值小于 0.05）：
Log-Rank 检验，每个时点有相同的权重，对后期的差异更为敏感，最为常用。
Breslow 检验，各时间点的观察例数为权重，例数越多权重越高，对前期的差异更为敏感。
Tarone-Ware 检验，结合以上两种方法，适合生存曲线有交叉的情况使用。
分析：
三种方法的 P 值均小于 0.05，可以认为水平呈现显著性，拒绝原假设，因此认为这两组的生存率存在差异（原假设为生存率无差异）。
输出结果 4：Kaplan-Meier 曲线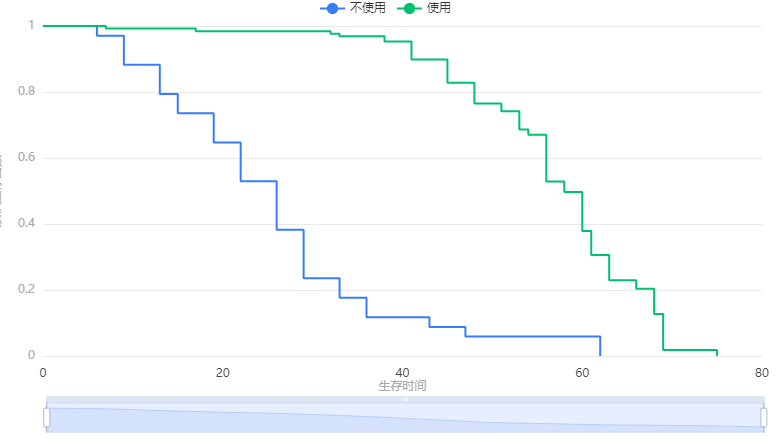
图表说明：
上图展示了 Kaplan-Meier 曲线，横轴为时间，纵轴为生存率，该曲线展示了随着时间变化生存率的变化情况。
分析：
从图可见使用新药相比未使用新药，能明显增加生存率。
# 7、注意事项
- 状态变量只能是二分类 0、1 变量，并且 1 代表是事件发生（如死亡/阳性等）；
- Kaplan-Meier 生存曲线在于研究某 1 个因素对于 Y 的影响，COX 回归研究多个因素对于 Y 的影响。
# 8、模型理论
Kaplan-Meier 算法（K-M 法）是由英国科学家 Kaplan 和 Meier 于 1958 年提出的，是利用概率乘法定理计算生存率，故又称乘积限法（Product-Limit Method，P-L 法），Kaplan-Meier 过程适用于小样本或大样本未分组资料生存率的 Kaplan-Meier 分析，生存率和组间生存率比较。
（1）Kaplan-Meier 生存曲线的画法：
1.在每个发生死亡事件的时间点上，进行生存率的计算
2.在每个发生删失的时间点上，画小竖线标记删失样本
3.根据观察/对照条件分组作图
（2）生存率的点估计
设 ni-1,ni,di 和 ci 分别表示活过时间 ti-1 且未在 ti-1 截尾的对象处、期初例数、死亡数和截尾数，则时间 ti 处的生存率估计为：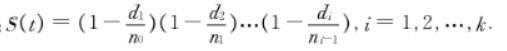
（3）生存率的区间估计
Greenwood 生存率标准误差的近似计算公式为：
假定生存率近似服从正态分布，则总体生存率的（1-α）置信区间为：
（4）生存率的组间比较
Log rank 检验是生存率比较的非参数方法之一，其基本思想是当 H0 成立时，根据 ti 时点的死亡率，可以计算出各组的理论死亡数，则
统计量的计算公式为：
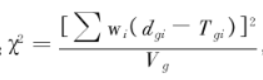
其中，Vg 为第 g 组理论数 Tg 的方差估计
。
对 Log rank 检验，wi=1，当比较的两总体生存曲线成比例时，检验效能最大；
wi=ni，则对应 Breslow 检验或 Wilcoxon 检验，该检验给实际死亡率与理论死亡数的早期差别最大的权重。
而在 Tarone-Ware 检验中，wi=√ni，其中 ni 表示时间 ti 处所对应的期初例数。近似服从自由度为（组数-1）的分布。由于该检验能对各组的生存率做整体比较，因此实际工作中应用较多。
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]金春林,王锦福,郑树忠.生存分析 Kaplan—meier 法简介[J].卫生软科学,1994(06):30-34.