多准则妥协解排序法（VIKOR）

# 1、作用

VIKOR 模型是一种对评价对象进行排序的方法。基本过程为首先计算评价对象总的最优解和最差解，然后比较各评价对象与最优解和最差解之间的距离大小来确定评价对象的排序，进而获得待评价对象的优劣级别。

# 2、输入输出描述

输入：至少两项或以上的定量变量。
输出：反应考核指标在量化评价中的综合得分。

# 3、案例示例

案例：医管局为了客观地评价我本市 10 家医院的运行情况根据门诊人数、病床使用率、确诊符合率和抢救成功率等进行评估。

# 4、案例数据

# 5、案例操作

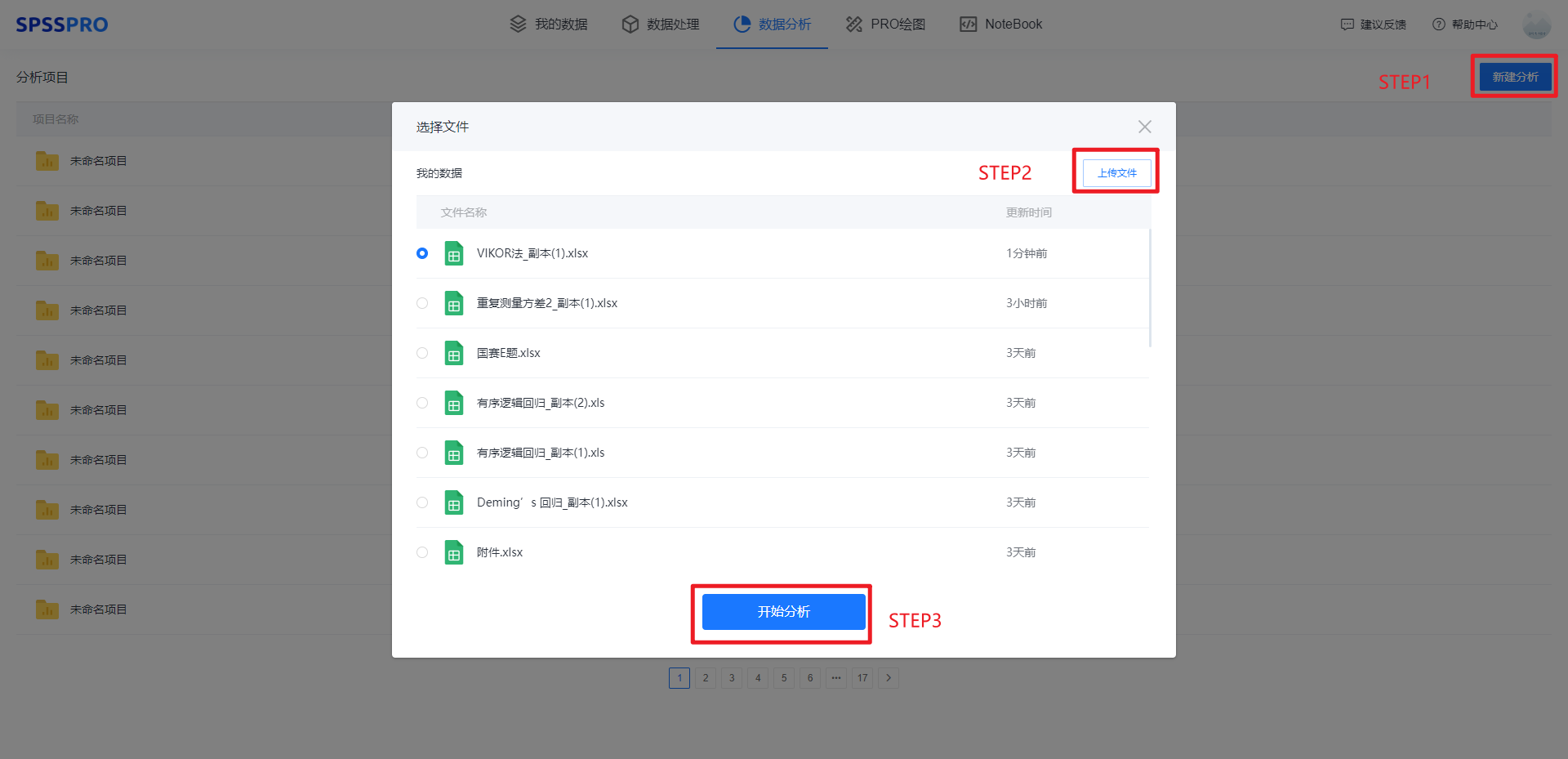
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；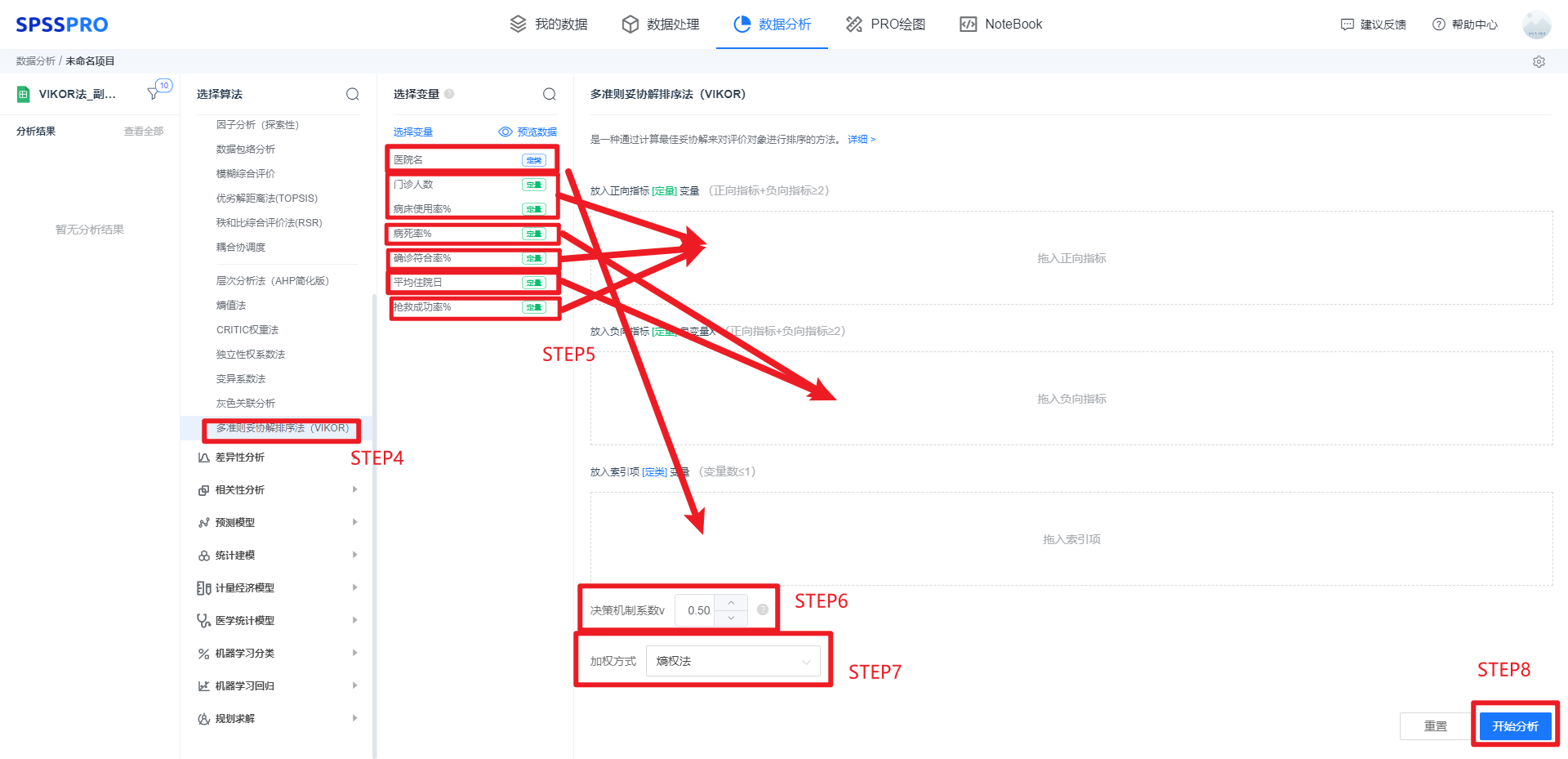

step4：选择【多准则妥协解排序法（VIKOR）】；
step5：查看对应的数据数据格式，【多准则妥协解排序法（VIKOR）】要求特征序列为定量变量，分为正向指标变量和负向指标变量，且正向指标变量和负向指标变量的个数之和大于等于两项；
step6：设置决策机制系数；
step7：设置加权方式，本例使用熵权法定权；
step8：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：指标权重计算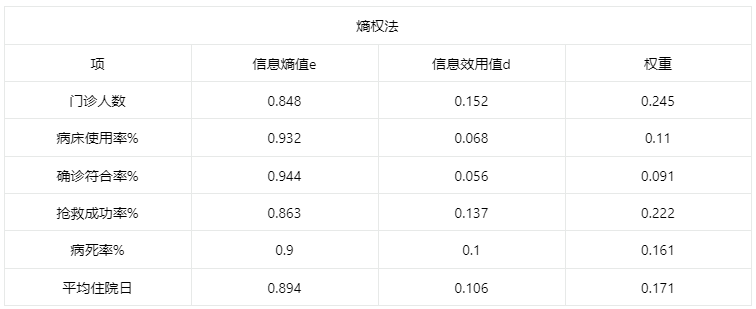

图表说明：
上表展示了熵权法的权重计算结果，根据结果对各个指标的权重进行分析。
图表说明：
熵权法的权重计算结果显示，门诊人数的权重为 24.512%、病床使用率%的权重为 10.997%、确诊符合率%的权重为 9.111%、抢救成功率%的权重为 22.173%、病死率%的权重为 16.132%、平均住院日的权重为 17.074%，其中指标权重最大值为门诊人数（24.512%），最小值为确诊符合率%（9.111%）。

输出结果 2：多准则妥协解排序法（VIKOR）总结

图表说明：
上表展示了在全部方案中群体效用值（S）和个体遗憾值（R）的最优值和最劣值。

输出结果 3：中间值展示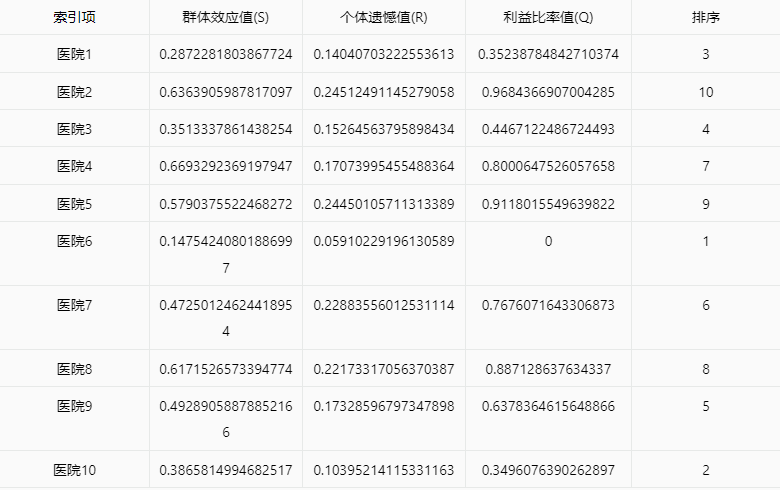

图表说明：
上表展示了多准则妥协解排序法（VIKOR）的计算结果，超过 15 行的数据需要下载至本地进行查看。
● 群体效用值（S）为各个评价方案到最优方案的加权距离(范数为 1 的闵可夫斯基距离)。其值越小越好，越小说明群体效应越大;
● 个体遗憾值（R）为各个评价方案到最优方案的加权距离(范数为无穷大的闵可夫斯基距离)。其值越小越好，越小说明个别遗憾越小;
● 根据群体效用值与个体遗憾值的结果，在此基础上计算决策指标 Q 值，指标 Q 值越小方案越优，最终得到排序。

# 7、注意事项

• 进行 VIKOR 分析时，各个指标有着权重属性（当然通常情况并没有），那么可对应设置各个指标的权重（输入的权重值可以为相对数字，SPSSPRO 默认都会进行归一化处理让权重加和为 1）。

# 8、模型理论

# 多准则妥协解排序法（VIKOR）介绍

VIKOR 法是由 Opricovic 教授于 1998 年提出的一种多属性决策方法。它基于 Lpmetric 聚合函数，通过确定“正理想解”和“负理想解”，计算各备选方案的折衷解，通过各备选方案与理想方案之间的接近程度在可接受优势和决策过程稳定的条件下对方案进行排序。
VIKOR 法考虑了决策者的主观偏好，其最大特色就是将最大化的 “群体效益”和最小化的“个体遗憾”相妥协，从而使该方法研究多属性决策问题更加合理 。VIKOR 法主要分为确定权重、计算理想解、计算群体效用值与个体遗憾值和计算利益比率并排序 5 个步骤。

# 确定权重

可以使用多种定权方法，常用的方法包括德尔菲法、熵权法、CRITIC 法、组合赋权法等。SPSSPRO 默认采用熵权法进行定权，如要采用其他方法，可以在自定义权重中输入其他方法计算出的权重。

# 计算理想解

正理想解是最大化正向指标并最小化负向指标的解决方案，而负理想解是最小化正向指标并最大化负向指标的解决方案。理想解的计算公式如下:
$f_j^{+}=1$
$f_j^{-}=0$
其中，$f_j^{+}$为第 j 个评价指标的正理想解，$f_j^{-}$为第 j 个评价指标的负理想解。

# 计算群体效用值与个体遗憾值

群体效用值是决策者们对得失效果的看法与态度的一种数量表示，用来衡量决策者对于某些事物的主观倾向和偏好。个体遗憾值是某个方案中其他值与最高值之间的差额，用来反映决策者错误判断所造成的损失价值。在计算群体效用值和个体遗憾值的过程中，VIKOR 法通常只采用了正理想解的信息而忽视了负理想解的信息。正理想解和负理想解虽然具有某种程度的相关性，但负理想解仍然具有自己特有的信息。因此，本文采用分别以正、负理 想解作为参照对群体效用值和个体遗憾值进行计算，计算公式如下所示：
以正理想解为参照：

以负理想解为参照：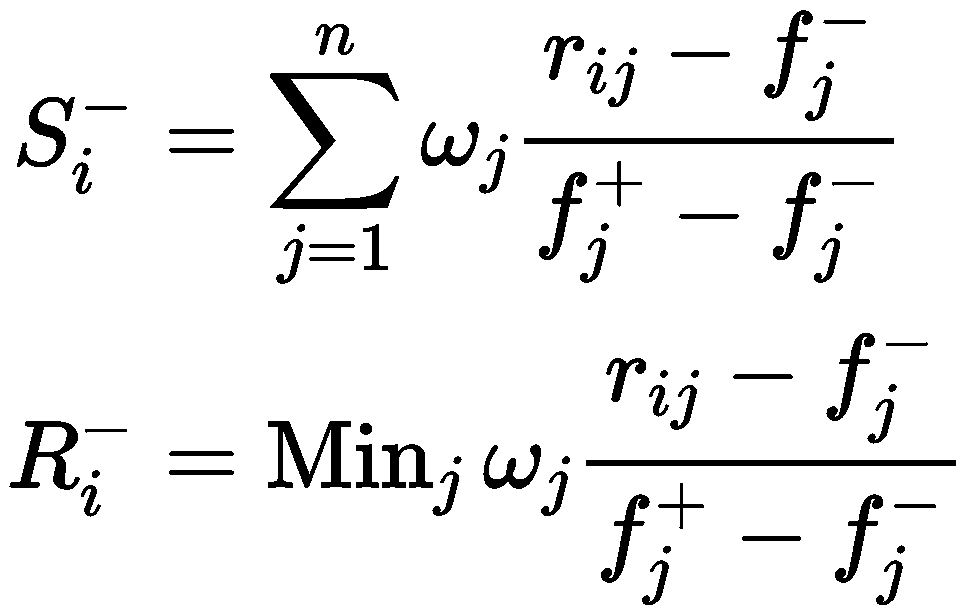

方案的群体效用值和个体遗憾值:
$S_i=\frac{S_i^{+}}{S_i^{-}}$
$R_i=\frac{R_i^{+}}{R_i^{-}}$
式中，$S_i^{+}$和$R_i^{+}$分别为第 i 个方案以正理想解为参照的群体效用值和个体遗憾值;
$S_i^{-}$和$R_i^{-}$分别为第 i 个方案以负理想解为参照的群体效用值和个体遗憾值;
$S_i$和$R_i$分别为第 i 个方案的群体效用值和个体遗憾值。

# 计算利益比率和排序

利益比率的计算结合了群体效用值与个体遗憾值，通过决策机制系数使得 VIKOR 法可以实现群体效用的最大化和个体遗憾的最小化。决策机制系数 v 越大表示决策中越注重最大群体化效用，越不注重反对者的个体遗憾。利益比率的结果按照降序排序，数值越小说明结果越好。
$Q_i=v\frac{S_i-S_{imin}}{S_{imax}-S_{imin}}+(1-v)\frac{R_i-R_{imin}}{R_{imax}-R_{imin}}$
$S_{imax}=max{S}_i$，$S_{imin}=min{S}_i$，$R_{imax}=max{R}_i$，$R_{imin}=min{R}_i$
其中，$Q_i$为利益比率，v 为决策机制系数。

# 9、手推步骤

# Step 1：数据标准化

对每个指标进行极差标准化，转换为0-1范围：

正向指标（门诊人数、病床使用率%、确诊符合率%、抢救成功率%）：

$r_{ij}^{\ast }=\frac{r_{ij}-\underset{j}{min}}{\underset{j}{max}-\underset{j}{min}}$

负向指标（病死率%、平均住院日）：

$r_{ij}^{\ast }=\frac{\underset{j}{max}-r_{ij}}{\underset{j}{max}-\underset{j}{min}}$

示例计算（医院6的门诊人数）

$\underset{j}{max}=368107$（医院1），$\underset{j}{min}=215654$（医院2）

标准化值：

$\frac{339841-215654}{368107-215654}=\frac{124187}{152453}\approx 0.815$

负向指标示例（医院6的病死率%）

$\underset{j}{max}=1.947$（医院7），$\underset{j}{min}=1.141$（医院9）

标准化值：

$\frac{1.947-1.205}{1.947-1.141}=\frac{0.742}{0.806}\approx 0.920$

# Step 2：熵权法计算权重

计算标准化数据占比 $p_{ij}$:

$p_{ij}=\frac{r_{ij}^{\ast }}{\sum _{i=1}^m{r}_{ij}^{\ast }}$

计算信息熵 $e_j$:

$e_j=-\frac{1}{\ln (m)}\sum _{i=1}^m{p}_{ij}\ln p_{ij}$

计算信息效用值 $d_j$:

$d_j=1-e_j$

计算权重 ${\omega }_j$:

${\omega }_j=\frac{d_j}{\sum _{j=1}^n{d}_j}$

示例计算（门诊人数的权重计算）： 标准化数据总和：

$\sum _{i=1}^{10}{r}_{ij}^{\ast }=0.815+0.0+0.845+\cdots \approx 6.532$

计算占比 $p_{ij}$（以医院6为例）：

$p_{6j}=\frac{0.815}{6.532}\approx 0.125$

信息熵 $e_j$：

$e_j=-\frac{1}{\ln (10)}(0.125\ln 0.125+\cdots )\approx 0.848$

权重：

${\omega }_j=\frac{1-0.848}{\sum d_j}=\frac{0.152}{0.619}\approx 0.245$

最终权重表：

# Step 3：计算群体效用值（$S$）和个体遗憾值（$R$）

公式：

$S_i=\sum _{j=1}^n{\omega }_j\cdot \frac{f_j^{+}-r_{ij}}{f_j^{+}-f_j^{-}}(\text{正向指标})$

$S_i=\sum _{j=1}^n{\omega }_j\cdot \frac{r_{ij}-f_j^{-}}{f_j^{+}-f_j^{-}}(\text{负向指标})$

$R_i=\underset{j}{max}({\omega }_j\cdot \frac{f_j^{+}-r_{ij}}{f_j^{+}-f_j^{-}})(\text{正向指标})$

$R_i=\underset{j}{max}({\omega }_j\cdot \frac{r_{ij}-f_j^{-}}{f_j^{+}-f_j^{-}})(\text{负向指标})$

示例计算（医院6的 $S$ 值和 $R$ 值计算）：

• 门诊人数（正向）：
  

  $S\mathrm{项}=0.245\cdot \frac{368107-339841}{368107-215654}=0.245\cdot 0.185\approx 0.045$

• 病床使用率%（正向）：
  

  $S\mathrm{项}=0.11\cdot \frac{101.961-98.766}{101.961-80.39}=0.11\cdot 0.148\approx 0.016$

• 病死率%（负向）：
  

  $S\mathrm{项}=0.161\cdot \frac{1.205-1.141}{1.947-1.141}=0.161\cdot 0.079\approx 0.013$

• 平均住院日（负向）:
  

  $S\mathrm{项}=0.171\cdot \frac{10.929-10.362}{12-10.362}=0.171\cdot 0.346\approx 0.059$

• 抢救成功率%（正向，医院6为最大值）：
  

  $S\mathrm{项}=0.222\cdot 0=0$

  群体效用值 $S_i$:
  

  $S_i=0.045+0.016+0.013+0.059+0=0.133$

  个体遗憾值 $R_i$:
  

  $R_i=max(0.045,0.016,0.013,0.059,0)=0.059$

# Step 4：计算利益比率（$Q$）

公式：

$Q_i=v\cdot \frac{S_i-S_{min}}{S_{max}-S_{min}}+(1-v)\cdot \frac{R_i-R_{min}}{R_{max}-R_{min}}$

其中，$v=0.5$，$S_{min}=0.148$，$S_{max}=0.669$，$R_{min}=0.059$，$R_{max}=0.245$

医院6的Q值计算：

$Q_6=0.5\cdot \frac{0.133-0.148}{0.669-0.148}+0.5\cdot \frac{0.059-0.059}{0.245-0.059}=0.5\cdot (-0.029)+0=-0.014(\text{取绝对值后为}0)$

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 尹夏楠, 朱莲美, 鲍新中. 基于 VIKOR 方法的高新技术企业成长性评价[J]. 财会通讯:上, 2015.
[3] 杨海燕,孙晓博,程小文,周广宇.基于 VIKOR 法的潍坊市水资源承载力综合评价[J].环境科学学报,2020,40(02):716-723.DOI:10.13671/j.hjkxxb.2019.0344.