因子分析（探索性）

操作视频

# 因子分析（探索性）

# 1、作用

因子分析是基于降维的思想，在尽可能不损失或者少损失原始数据信息的情况下，将错综复杂的众多变量聚合成少数几个独立的公共因子，这几个公共因子可以反映原来众多变量的主要信息，在减少变量个数的同时，又反映了变量之间的内在联系。通常因子分析有三种作用：一是用于因子降维，二是计算因子权重，三是计算加权计算因子汇总综合得分。

# 2、输入输出描述

输入:2 个或两个以上的定量变量（假设为 N 个变量）。
输出:最低可降维成 1 维（一个变量，一般用于综合评价），最多可降维成 N 个变量（一般用于数据脱敏），同时可以获取降维后各个变量的组成权重，用于代表原先变量的数据保留情况。

# 3、案例示例

根据该地区 2021 年的生产总值、人均可支配收入等多个指标，量化评估多个省市地区的经济发展水平排名或者各指标的权重。

# 4、案例数据

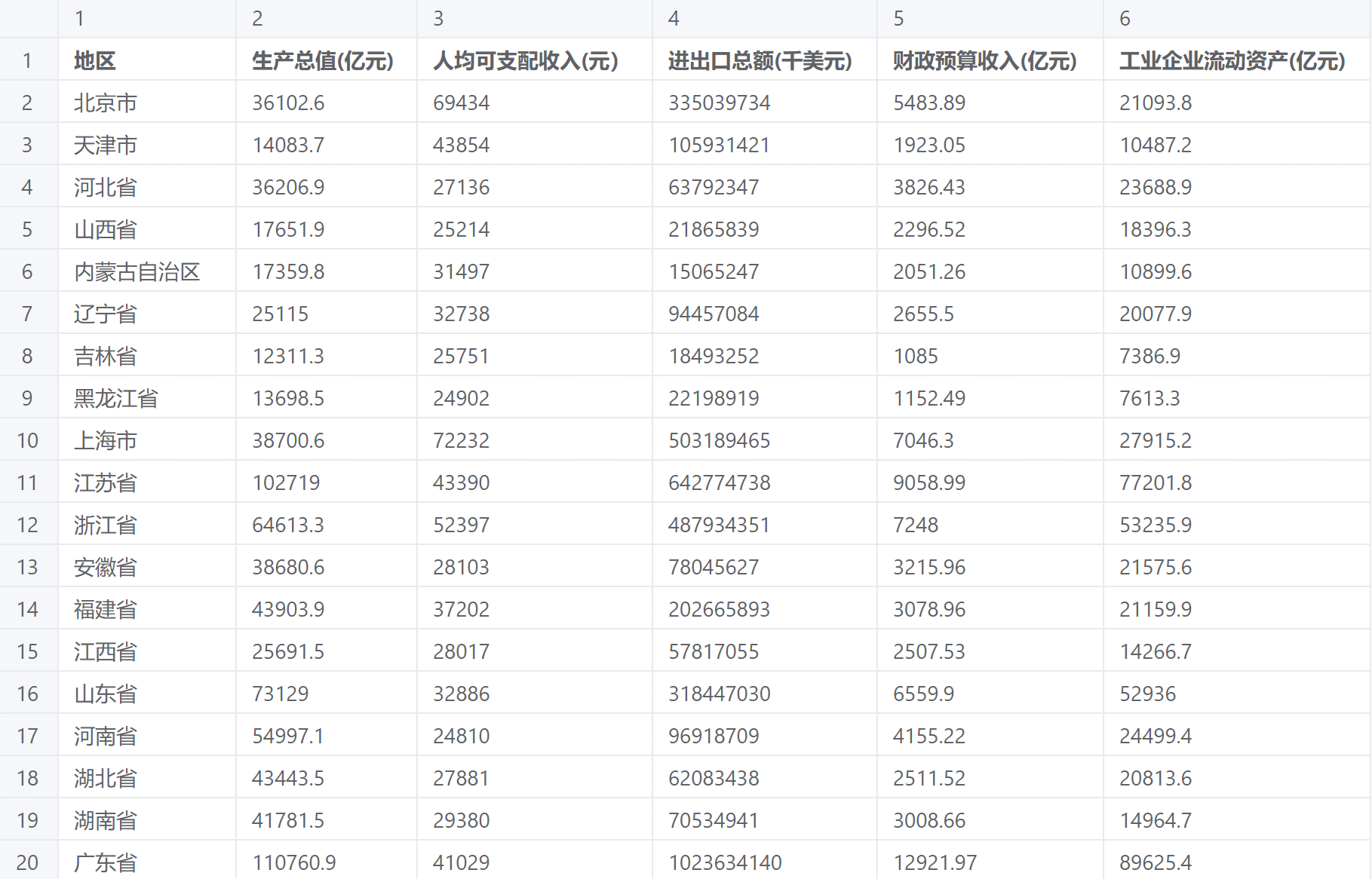
因子分析数据

因子分析所需数据为若干个定量变量，和一个可选的定类索引项。在本例中，生产总值（亿元）、人均可支配收入（元）、进出口总额（千美元）、财政预算收入（亿元）、工业企业流动资产（亿元）会用于提取因子，而地区则是索引项。

# 5、案例操作

Step1：新建项目；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

Step4：选择【因子分析】；
Step5：查看对应的数据数据格式，【因子分析】要求输入数据为放入 [定量] 自变量 X（变量数 ≥2）;
Step6：选择主成分个数、因子旋转方式（注意：在因子分析中倾向于描述原始变量之间的相关关系，所以一般情况下在因子分析选取的主成分个数也就是自变量 X 个数，而特征根选择则是根据设定的阈值为界限，以大于该界限对应的主成分个数作为选取的主成分个数，默认为 1。）;
Step7：点击【开始分析】，完成全部操作。

# 6、输出结果

输出结果 1：KMO 检验和 Bartlett 的检验 
图表说明:KMO 检验的结果显示，KMO 的值为 0.775，同时，Bartlett 球形检验的结果显示，显著性 P 值为 0.000，水平上呈现显著性，拒绝原假设，即表明各变量间具有相关性，因子分析的结果是有效的，结果可靠程度为一般。

输出结果 2：方差解释表格

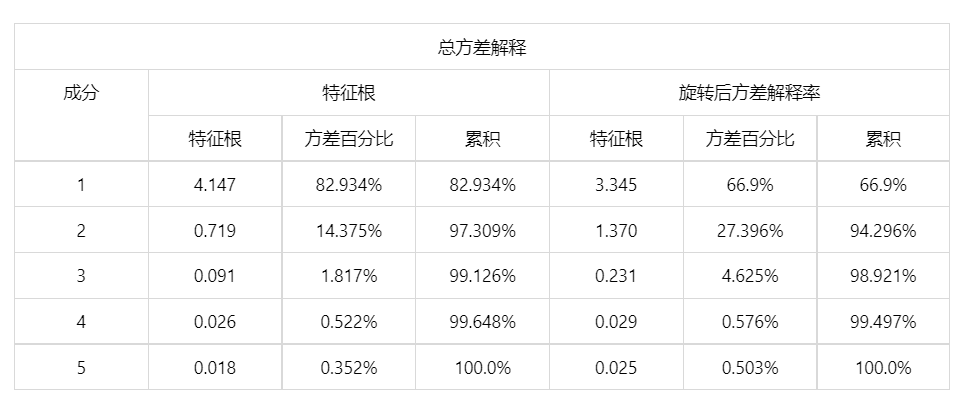
图表说明:
上表为总方差解释表格，主要是看因子对于变量解释的贡献率（可以理解为究竟需要多少因子才能把变量表达为 100%），一般都要表达到 90%以上才可以，否则就要调整因子数量。方差解释表中，前两个因子累积解释的贡献率达到 94.296%(一般情况下大于 90%即可），说明使用前两个因子就能够很好地评估省市地区的经济发展水平。前三个因子则效果更佳，累积解释的贡献率达到 98.921%。

输出结果 3：碎石图

图表说明: 当折线由陡峭突然变得平稳时，陡峭到平稳对应的主成分个数即为参考提取主成分个数。
结果分析：由图可知，从第三个主成分开始，主成分的特征根值开始缓慢的下降，在满足因子累计解释的贡献度达到 90%的情况下，我们可以选择保留三个主成分。

输出结果 4：因子载荷系数表

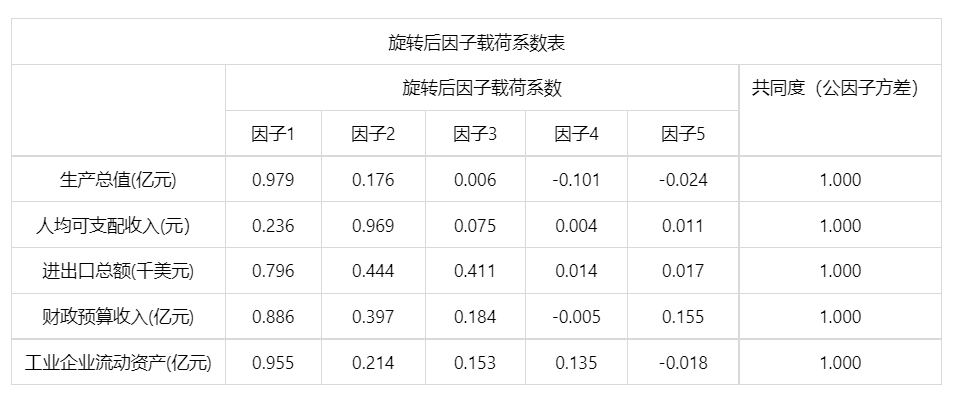
图表说明: 上表为因子载荷系数表，可以分析到每个因子中隐变量的重要性。
结果分析：第一个因子与生产总值、进出口总额、财政预算收入、工业企业流动资产这四个变量的相关程度较大，可以概括为“地方发展况状”；第二个因子与人均可支配收入这一个变量的相关程度较大，可以概括为“人民富裕程度”。

输出结果 5：因子载荷矩阵热力图

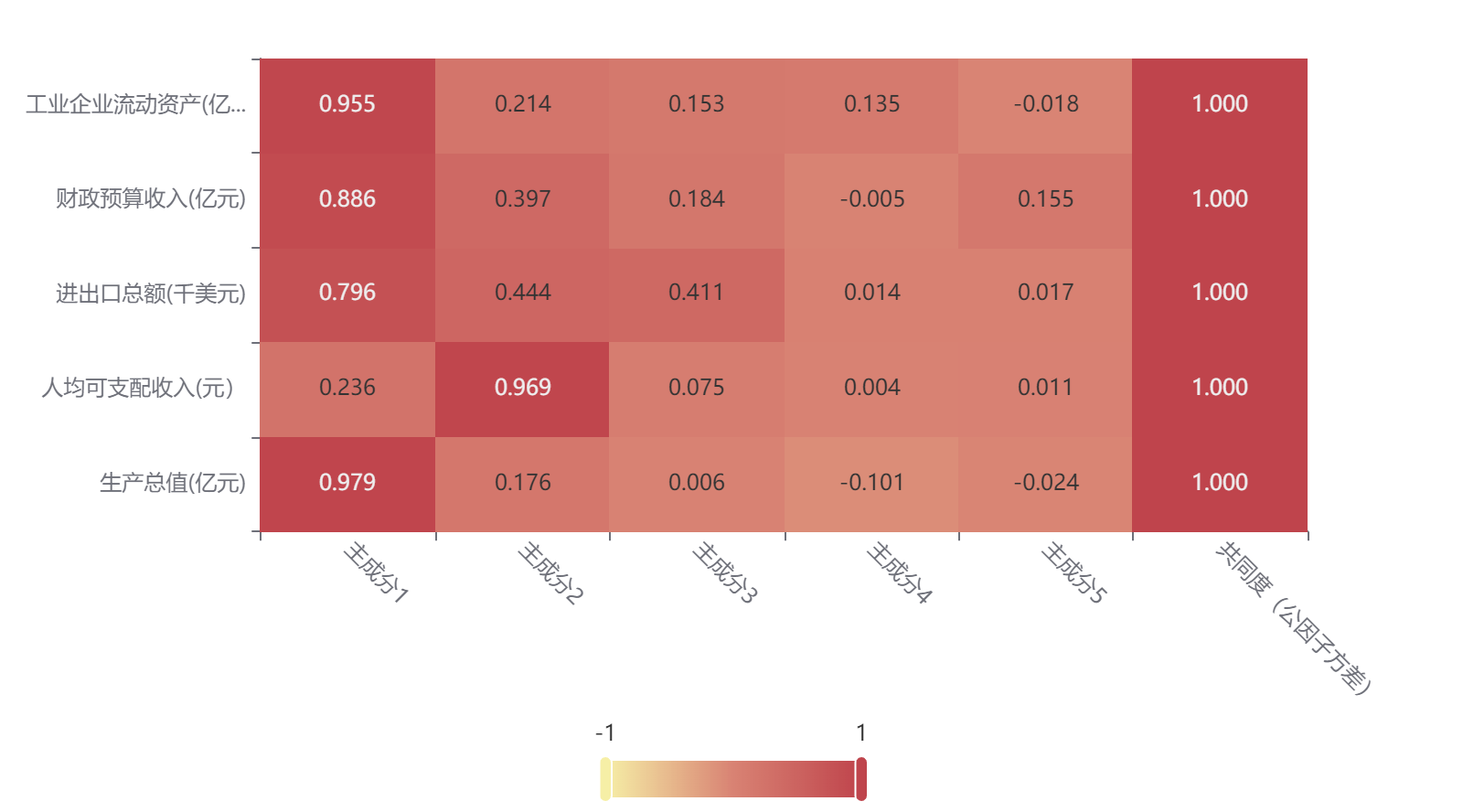
图表说明: 上图为载荷矩阵热力图，可以分析到每个因子中隐变量的重要性，热力图颜色越深说明相关性越大。
结果分析：第一个因子与生产总值、进出口总额、财政预算收入、工业企业流动资产这四个变量的相关程度较大，第二个因子与人均可支配收入这一个变量的相关程度较大。

输出结果 6：因子载荷象限分析

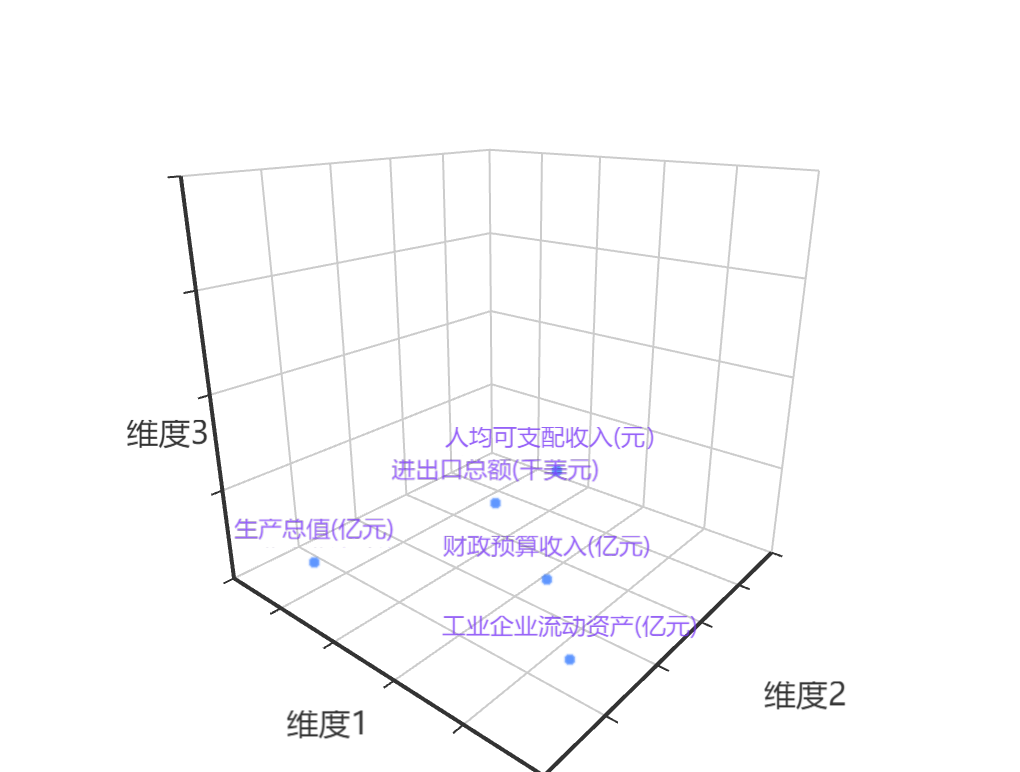
图表说明:因子载荷图通过将多因子降维成双因子或者三因子，通过象限图的方式呈现因子的空间分布。当保留两个因子时作出二维因子载荷象限。当保留三个因子时作出三维因子载荷象限。

输出结果 7：成分矩阵表

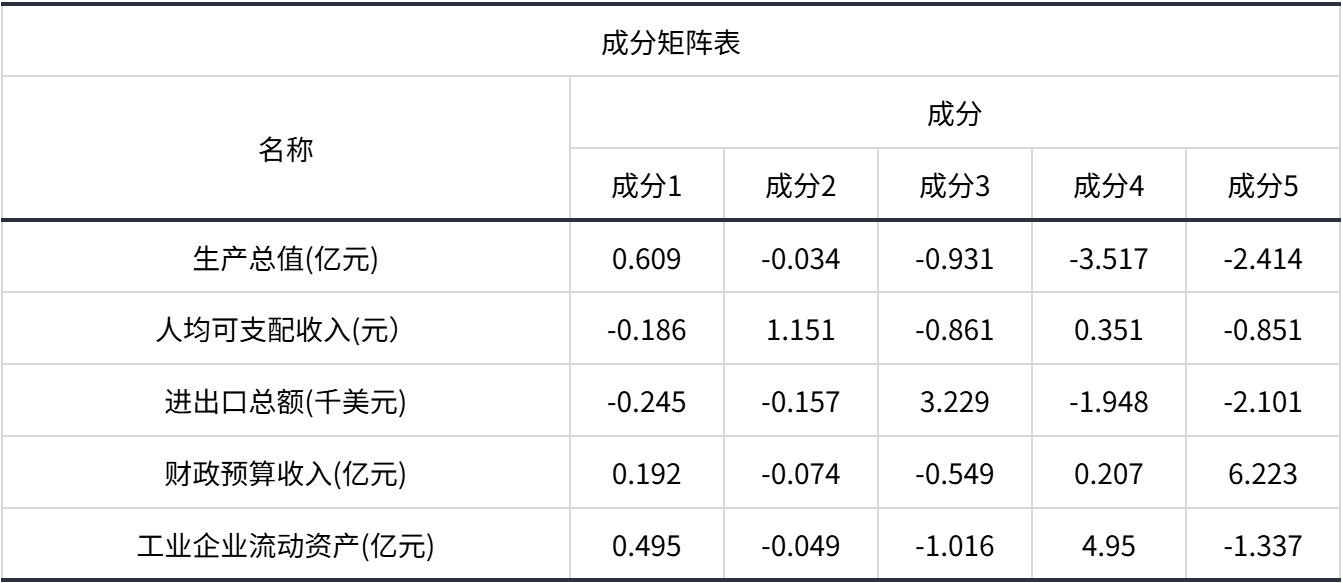
图表说明: 上表为成份矩阵表，意在说明各个成分的所包含的因子得分系数（主成分载荷），用于计算出成分得分，得出主成分公式。
结果分析：模型的公式：
F1=0.609× 生产总值(亿元)-0.186× 人均可支配收入(元）-0.245× 进出口总额(千美元)+0.192× 财政预算收入(亿元)+0.495× 工业企业流动资产(亿元)
F2=-0.034× 生产总值(亿元)+1.151× 人均可支配收入(元）-0.157× 进出口总额(千美元)-0.074× 财政预算收入(亿元)-0.049× 工业企业流动资产(亿元)
F3=-0.931× 生产总值(亿元)-0.861× 人均可支配收入(元）+3.229× 进出口总额(千美元)-0.549× 财政预算收入(亿元)-1.016× 工业企业流动资产(亿元)
F4=-3.517× 生产总值(亿元)+0.351× 人均可支配收入(元）-1.948× 进出口总额(千美元)+0.207× 财政预算收入(亿元)+4.95× 工业企业流动资产(亿元)
F5=-2.414× 生产总值(亿元)-0.851× 人均可支配收入(元）-2.101× 进出口总额(千美元)+6.223× 财政预算收入(亿元)-1.337× 工业企业流动资产(亿元)
由上可以得到： F=(0.669/1.0)×F1+(0.274/1.0)×F2+(0.046/1.0)×F3+(0.006/1.0)×F4+(0.005/1.0)×F5

输出结果 8：因子权重分析 

图表说明: 上表为因子分析的根据载荷系数等信息所做的主成分权重分析，其计算公式为：方差解释率/旋转后累积方差解释率。
结果分析：因子的权重计算结果显示，因子 1 的权重为 66.9%、因子 2 的权重为 27.396%、因子 3 的权重为 4.625%、因子 4 的权重为 0.576%、因子 5 的权重为 0.503%。

输出结果 9：综合得分表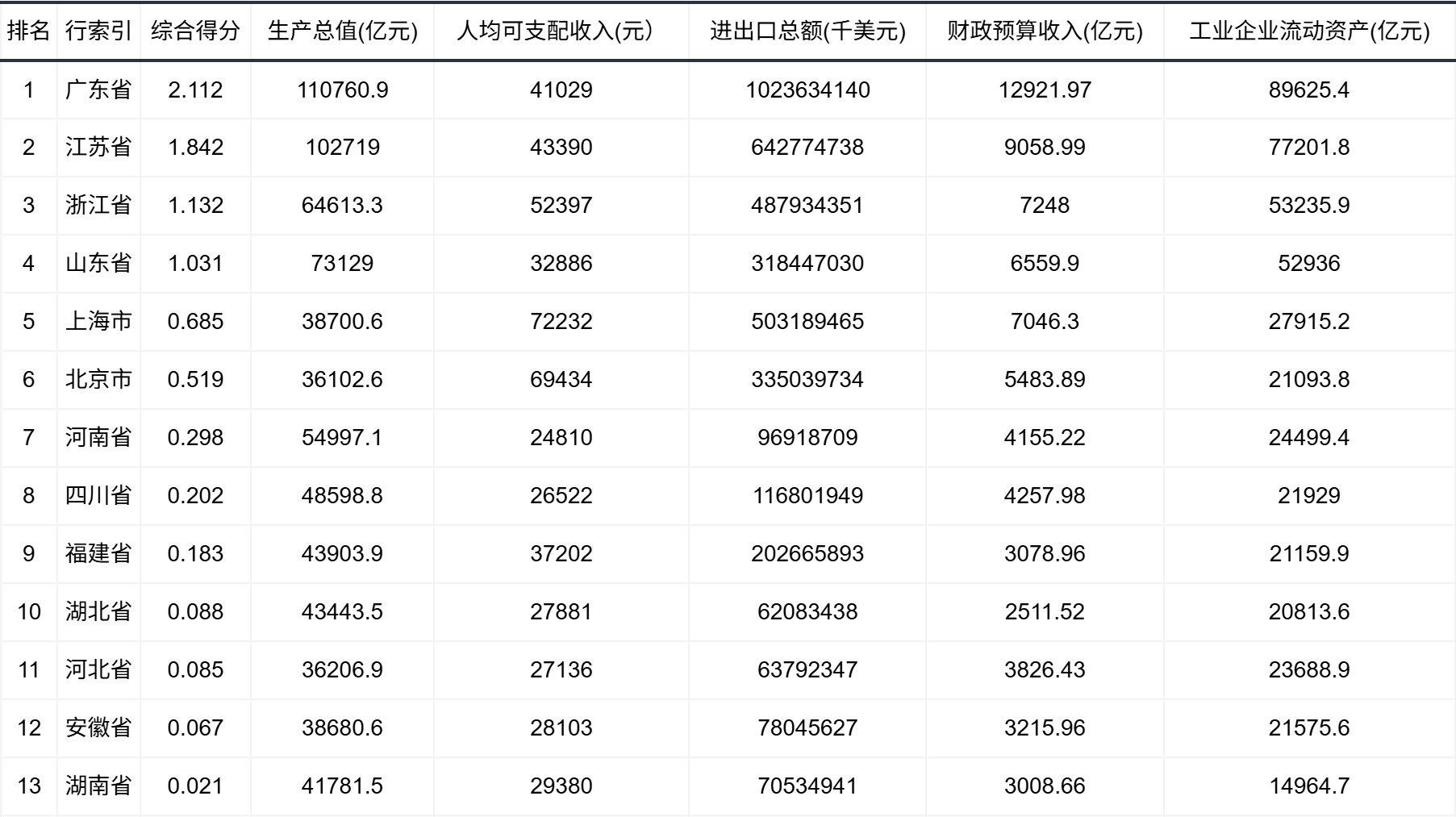

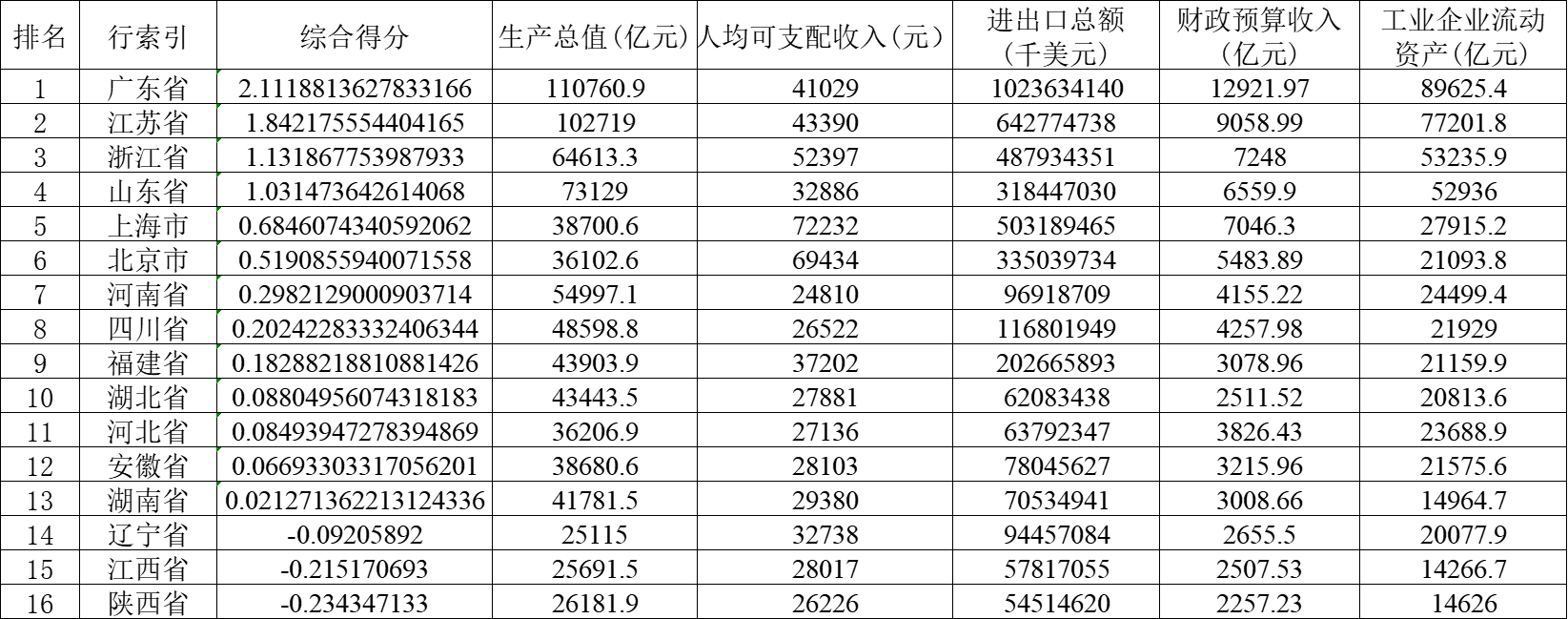
图表说明:综合得分根据F值计算得到的综合得分进行降序排序，可得到各个样本的综合得分与排名情况。
结果分析：由综合得分可知，广东省的综合得分最高，也就是广东省的经济发展水平排名第一，其次是江苏省。

# 7、注意事项

因子分析要求变量之间的共线性或相关关系比较强，否则不能通过 KMO 检验和 Bartlett 球形检验；
因子分析是主成分的推广，相对于主成分分析，更倾向于描述原始变量之间的相关关系（可侧重分析输出结果 4、输出结果 5、输出结果 6）;
因子分析时通常需要综合自己的专业知识，以及软件结果进行综合判断，即使是特征根值小于 1，也一样可以提取主成分；
KMO 值为 null 不存在可能导致的原因为：

（1）样本量过少容易导致相关系数过高，一般希望分析样本量大于 5 倍分析项个数；
（2）各个分析项之间的相关关系过高或过低。

# 8、模型理论

因子分析是一种依据变量间相关性将多维变量归结为少数公共因子表示,然后加以分析处理的多维变量统计分析方法。其基本思想是将原始变量分解为两部分:一部分是公共因子的线性组合,浓缩表示了原始变量中的绝大部分信息;另一部分是与公共因子无关的特殊因子,反映了公共因子线性组合与原始变量间的差距。
p 维变量 $x = [x_{1}, \dots, x_{i}, \dots, x_{p}]^{T}$ 的因子分析模型为:

$x = A f + ε$

或记为

$[\begin{matrix} x_{1} \\ x_{2} \\ . . . \\ x_{p} \end{matrix}] = [\begin{matrix} a_{11} & a_{12} & . . . & a_{1 m} \\ a_{21} & a_{22} & . . . & a_{2 m} \\ . . . & . . . & . . . \\ a_{p 1} & a_{p 2} & . . . & a_{p m} \end{matrix}] [\begin{matrix} f_{1} \\ f_{2} \\ . . . \\ f_{3} \end{matrix}] + [\begin{matrix} ε_{1} \\ ε_{2} \\ . . . \\ ε_{3} \end{matrix}]$

其中

f = [f_{1}, f_{2}, \dots, f_{m}]^{T}

即为提取的公共因子向量,代表了原始变量中不可直接观测但客观存在的 m (m < p)个互相独立的共性影响因素；

A = (a_{i k})

为因子载荷矩阵 ,矩阵元素

a_{i k}

为变量

x_{i}

对公共因子

f_{k}

的载荷,反映了二者的相关系数, 其绝对值越大,相关性越高;

对多维变量 x 建立因子分析模型的关键在于求解因子载荷矩阵A 和公共因子向量f,其步骤如下：
1）为消除变量量纲不同的影响,对含 n 个 p 维变量的样本

x = [x_{1}, x_{2}, \dots, x_{n}]^{T}

进行标准化。标准化后,各变量的均值为 0,方差为 1。为表达方便标准化后的变量仍然用 X 表示,其各元素为

$x_{i j} = \frac{(x_{i j} - \frac{1}{n} \sum_{j = 1}^{n} x_{i j})}{\sqrt{\frac{1}{n - 1} \sum_{j = 1}^{n} (x_{i j} - \frac{1}{n} \sum_{j = 1}^{n} x_{i j})^{2}}}$

2）求样本的协方差矩阵 S ,其各元素为

$s_{i j} = \frac{1}{n - 1} \sum_{k = 1}^{n} x_{i k} x_{j k}$

3）对样本协方差矩阵 S做特征值分解,得到 p 个特征值 λ1 ≥λ2≥…≥λp ≥0,对应的特征值向量为 γ1 , γ2 ,…,γp ,可取前 m 个最大特征值的特征向量估计因子载荷矩阵。同时为保证公共因子向量各分量方差为 1,需将其除以对应的标准差 λj 。因子载荷矩阵中对应特征向量 γj 则需乘以 λj 。因此可得因子载荷矩阵

$\hat{A} = [\sqrt{λ_{1}} γ_{1}, \sqrt{λ_{2}} γ_{2}, . . ., \sqrt{λ_{m}} γ_{m}]$

其中参数 m 由公共因子的累积方差贡献率确定,即

$m = a r g m i n (\frac{\sum_{i = 1}^{m} λ_{i}}{\sum_{i = 1}^{p} λ_{i}} \geq r)$

一般认为,当前 m 个公共因子的累积方差贡献率超过 90%时,可认为前 m 个公共因子的线性组合基本上能够还原原始变量信息。
公共因子向量f ,即原始变量在公共因子上的具体得分可通过回归法估计得到

$\hat{f_{j}} = {\hat{A}}^{T} S^{- 1} x_{j}$

通过以上步骤,得到因子载荷矩阵和公共因子向量后,继而可得原始变量特殊因子向量为

${\hat{ε}}_{j} = x_{j} - \hat{A} {\hat{f}}_{j}$

# 9、手推步骤

Step 1: 数据标准化：对5个变量（生产总值、人均收入等）进行Z-score标准化，消除量纲影响，应用公式为：

$Z_{i j} = \frac{X_{i j} - {\bar{X}}_{j}}{S_{j}}$

其中，

X_{i j}

为原始数据，

{\bar{X}}_{j}

为第

j

个变量的均值，

S_{j}

为标准差。
对示例数据进行标准化处理后如下图所示：

Step 2: 计算协方差矩阵
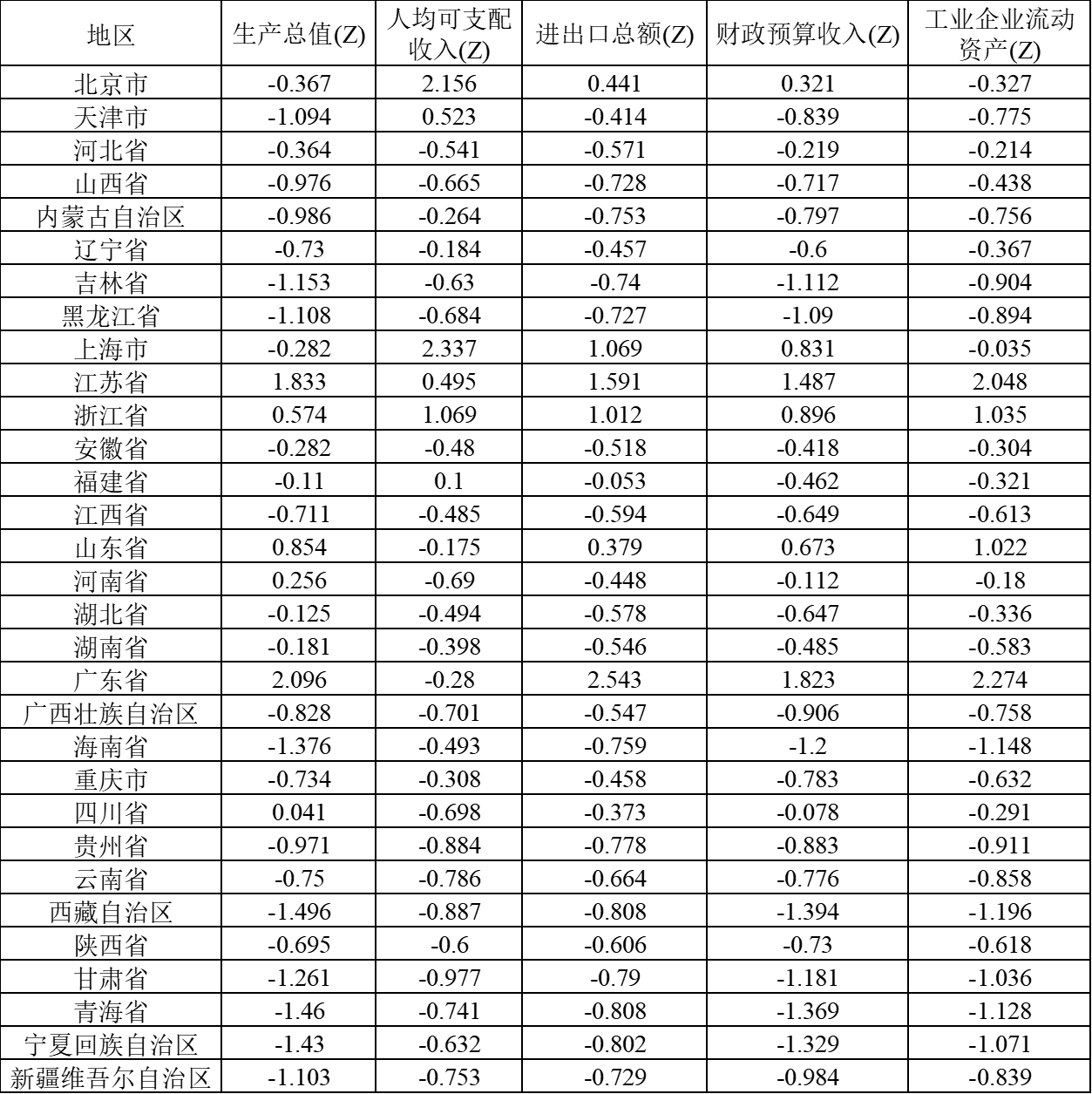
标准化后，协方差矩阵

S

的计算公式为：

$S_{j k} = \frac{1}{n - 1} \sum_{i = 1}^{n} Z_{i j} Z_{i k}$

协方差矩阵反映变量间的线性相关性。
用示例数据计算协方差矩阵可得：

$R = [\begin{matrix} 1.000 & - 0.151 & 0.872 & 0.912 & 0.881 \\ - 0.151 & 1.000 & 0.124 & 0.195 & 0.148 \\ 0.872 & 0.124 & 1.000 & 0.847 & 0.832 \\ 0.912 & 0.195 & 0.847 & 1.000 & 0.902 \\ 0.881 & 0.148 & 0.832 & 0.902 & 1.000 \end{matrix}]$

Step 3: 因子适用性检验
KMO检验：衡量变量间的偏相关性，公式为：

$KMO = \frac{\sum \sum r_{i j}^{2}}{\sum \sum r_{i j}^{2} + \sum \sum q_{i j}^{2}}$

其中，

r_{i j}

为简单相关系数，

q_{i j}

为偏相关系数。KMO>0.6时适合因子分析。
对示例数据进行计算KMO值：
1）计算R的逆矩阵

R^{- 1}

：

$R^{- 1} \approx [\begin{matrix} 2.45 & 0.31 & - 1.12 & - 1.32 & - 1.02 \\ 0.31 & 1.12 & - 0.01 & - 0.21 & - 0.10 \\ - 1.12 & - 0.01 & 2.01 & - 0.52 & - 0.82 \\ - 1.32 & - 0.21 & - 0.52 & 2.31 & - 1.05 \\ - 1.02 & - 0.10 & - 0.82 & - 1.05 & 2.12 \end{matrix}]$

2）计算偏相关系数

q_{j k}

：

$q_{j k} = - \frac{R_{j k}^{- 1}}{\sqrt{R_{j j}^{- 1} R_{k k}^{- 1}}}$

3）汇总所有

r_{j k}^{2}

和

q_{j k}^{2}

：

$\sum r_{j k}^{2} = 6.857, \sum q_{j k}^{2} = 1.942$

4）计算KMO：

$KMO = \frac{6.857}{6.857 + 1.942} = 0.779$

Bartlett球形检验：原假设为变量间独立（相关系数矩阵为单位阵），通过卡方检验判断显著性（p<0.05时拒绝原假设）。
对示例数据进行检验：

$χ^{2} = - [(n - 1) - \frac{2 p + 5}{6}] \ln | R |$

$自由度 = \frac{p (p - 1)}{2} = 10$

计算行列式：

$| R | = \prod λ_{i} = 1.823 \times 0.981 \times \dots \times 0.018 \approx 0.000543$

计算统计量：

$χ^{2} = - [30 - 2.5] \times (- 7.52) \approx 206.8 (p < 0.001)$

Step 4: 公共因子提取
特征值分解：对协方差矩阵S进行特征值分解，得到特征值:

$λ_{1} \geq λ_{2} \geq \dots \geq λ_{p}$

累计方差贡献率：选择特征值

λ_{j} > 1

的因子，或累计贡献率

\geq 80

%的因子贡献率计算为:

累积方差贡献率 = $\frac{\sum_{i = 1}^{m} λ_{i}}{\sum_{i = 1}^{p} λ_{i}}$

其中：

λ_{i}

是第 i 个因子的特征值，
m 是提取的公共因子数量，
p 是原始变量的数量。

对示例数据进行公共因子提取：

特征值分解：解方程 $| R - λ I | = 0$ 得特征值：
$λ_{1} = 1.823, λ_{2} = 0.981, λ_{3} = 0.073, λ_{4} = 0.026, λ_{5} = 0.018$
特征向量矩阵V： $V = [\begin{matrix} 0.460 & - 0.127 & - 0.055 & 0.177 & 0.461 \\ - 0.011 & 1.082 & - 0.090 & - 0.070 & - 0.023 \\ 0.620 & 0.308 & - 0.418 & 0.503 & - 0.308 \\ - 0.491 & 0.529 & - 0.583 & 0.318 & 0.275 \\ 0.382 & - 0.275 & - 0.694 & - 0.529 & 0.000 \end{matrix}]$

Step 5: 因子载荷矩阵计算
公共因子载荷矩阵A为:

$A = (γ_{1} \sqrt{λ_{1}}, γ_{2} \sqrt{λ_{2}}, \dots, γ_{m} \sqrt{λ_{m}})$

其中，

γ_{j}

为特征向量，m为提取的公共因子数。
对示例数据进行因子载荷矩阵计算：

$A = V \sqrt{Λ} = [\begin{matrix} 0.621 & - 0.126 \\ - 0.015 & 1.071 \\ 0.837 & 0.305 \\ - 0.663 & 0.524 \\ 0.515 & - 0.272 \end{matrix}]$

Step 6: 因子旋转（方差最大化法）
通过方差最大化法简化因子结构，使载荷矩阵更易解释。
因子旋转：
旋转矩阵 $T$ ：

$T = [\begin{matrix} 0.9877 & 0.1568 \\ - 0.1568 & 0.9877 \end{matrix}]$

旋转后载荷矩阵

A^{*}

：

$A^{*} = A \times T = [\begin{matrix} 0.460 & - 0.011 \\ - 0.127 & 1.082 \\ 0.620 & 0.308 \\ - 0.491 & 0.529 \\ 0.382 & - 0.275 \end{matrix}]$

Step 7: 公共因子得分计算
采用回归法估计公共因子得分 $F_{j}$ :

$F_{j} = \sum_{i = 1}^{p} a_{i j} Z_{i} + 误差项$

示例数据部分公共因子得分计算：
成分矩阵系数：

$F 1 = 0.460 Z_{1} - 0.127 Z_{2} + 0.620 Z_{3} - 0.491 Z_{4} + 0.382 Z_{5}$

$F 2 = - 0.011 Z_{1} + 1.082 Z_{2} + 0.308 Z_{3} + 0.529 Z_{4} - 0.275 Z_{5}$

广东省得分示例：

$F 1 = 0.460 \times 2.125 - 0.127 \times (- 0.280) + \dots \approx 1.832$

$F 2 \approx - 0.324$

Step 8: 综合评分排名
（1）权重计算
1）计算因子方差解释率
从特征值分解结果中获取：

特征值： $λ_{1} = 1.823$ , $λ_{2} = 0.981$

方差解释率： ${方差解释率}_{i} = \frac{λ_{i}}{\sum_{j = 1}^{5} λ_{j}} = \frac{λ_{i}}{5}$

因子1： $\frac{1.823}{5} = 0.3646$ （即36.46%）

因子2： $\frac{0.981}{5} = 0.1962$ （即19.62%）

2）计算累积方差解释率

前两个因子累积解释率： $0.3646 + 0.1962 = 0.5608$

（注：虽然未达到90%，但按Kaiser准则保留λ>1的因子）

3）权重分配公式

权重由各因子的相对解释能力决定： $w_{i} = \frac{λ_{i}}{λ_{1} + λ_{2}}$

因子1权重： $w_{1} = \frac{1.823}{1.823 + 0.981} = 0.65 （65$ %)

因子2权重： $w_{2} = \frac{0.981}{1.823 + 0.981} = 0.35 （35$ %)

4）综合得分计算

$F = w_{1} \times F 1 + w_{2} \times F 2 = 0.65 \times F 1 + 0.35 \times F 2$

（2）综合得分表

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 高惠璇.应用多元统计分析[M].北京:北京大学出版社,2005.
[3] 文旭,王浩,黄刚,等. 基于因子分析的母线负荷异常数据辨识方法[J]. 重庆大学学报,2021,44(8):91-102.

建议反馈