独立性权系数法

# 1、作用

独立性权系数法是一种客观赋权法。其思想在于根据各指标与其他指标之间的共线性强弱来确定指标权重的，若指标之间的共线性关系越强，越容易由其他指标的线性组合表示，重复信息越多，因此该指标的权重也就应该越小。

# 2、输入输出描述

输入：至少两项或以上的定量变量。
输出：输入定量变量对应的权重值

# 3、案例示例

案例：数据是 100 个客户的各方面（能力，品格，担保，资本，环境）评分，利用独立性权系数法来计算各个变量（能力，品格，担保，资本，环境）的重要性，即所占的权重。
（注意：若是各个指标之间的单位和量级(即计量指标的数量级)不同，在进行分析前需要自行对数据进行归一化）

# 4、案例数据

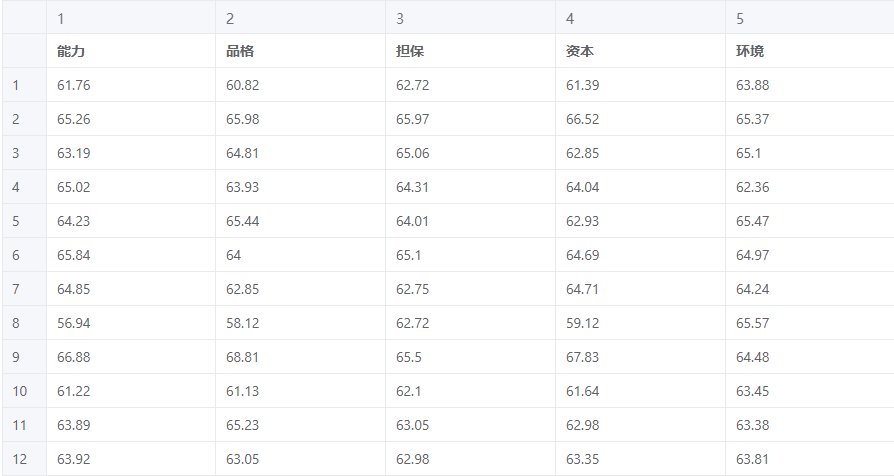
# 5、案例操作

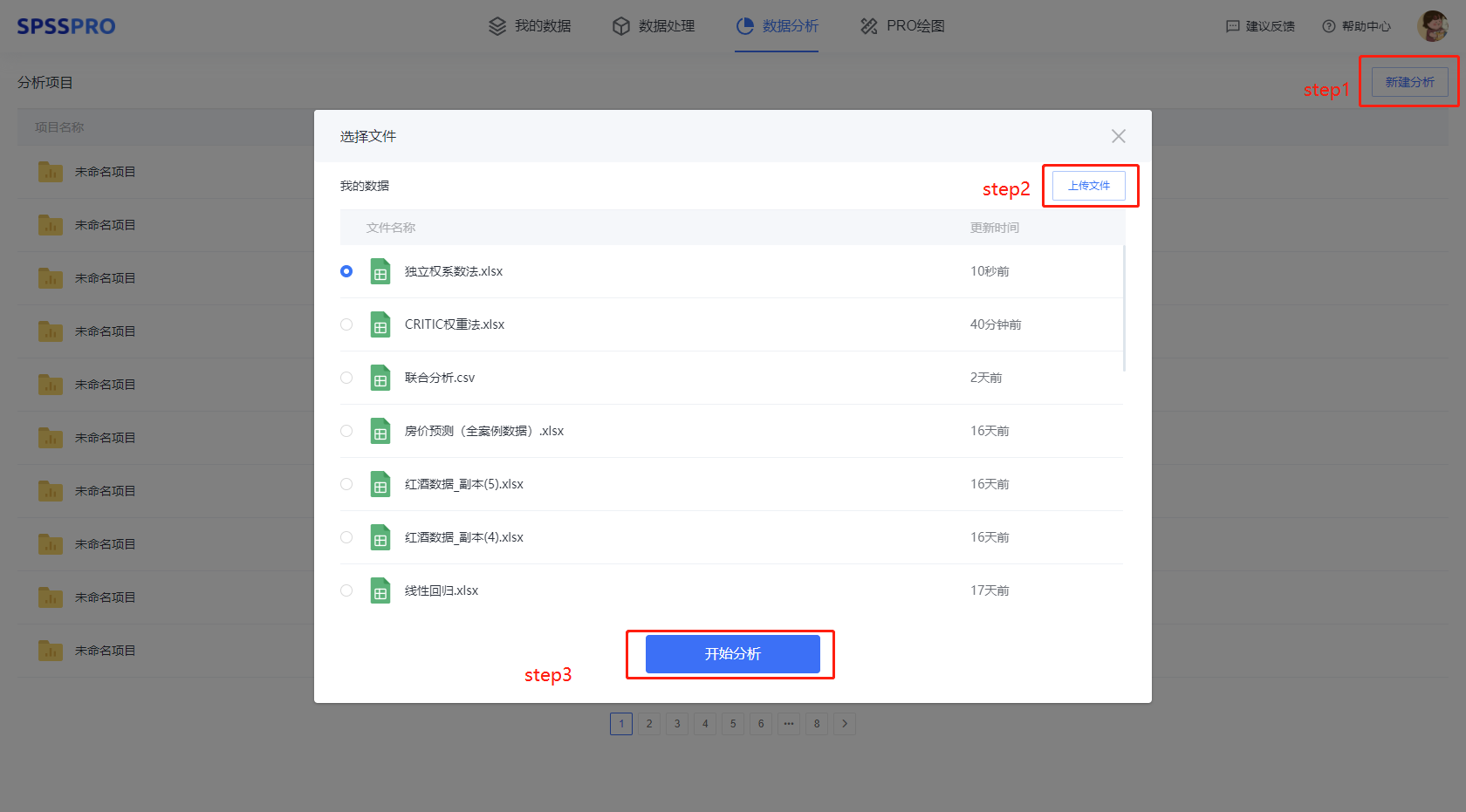
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；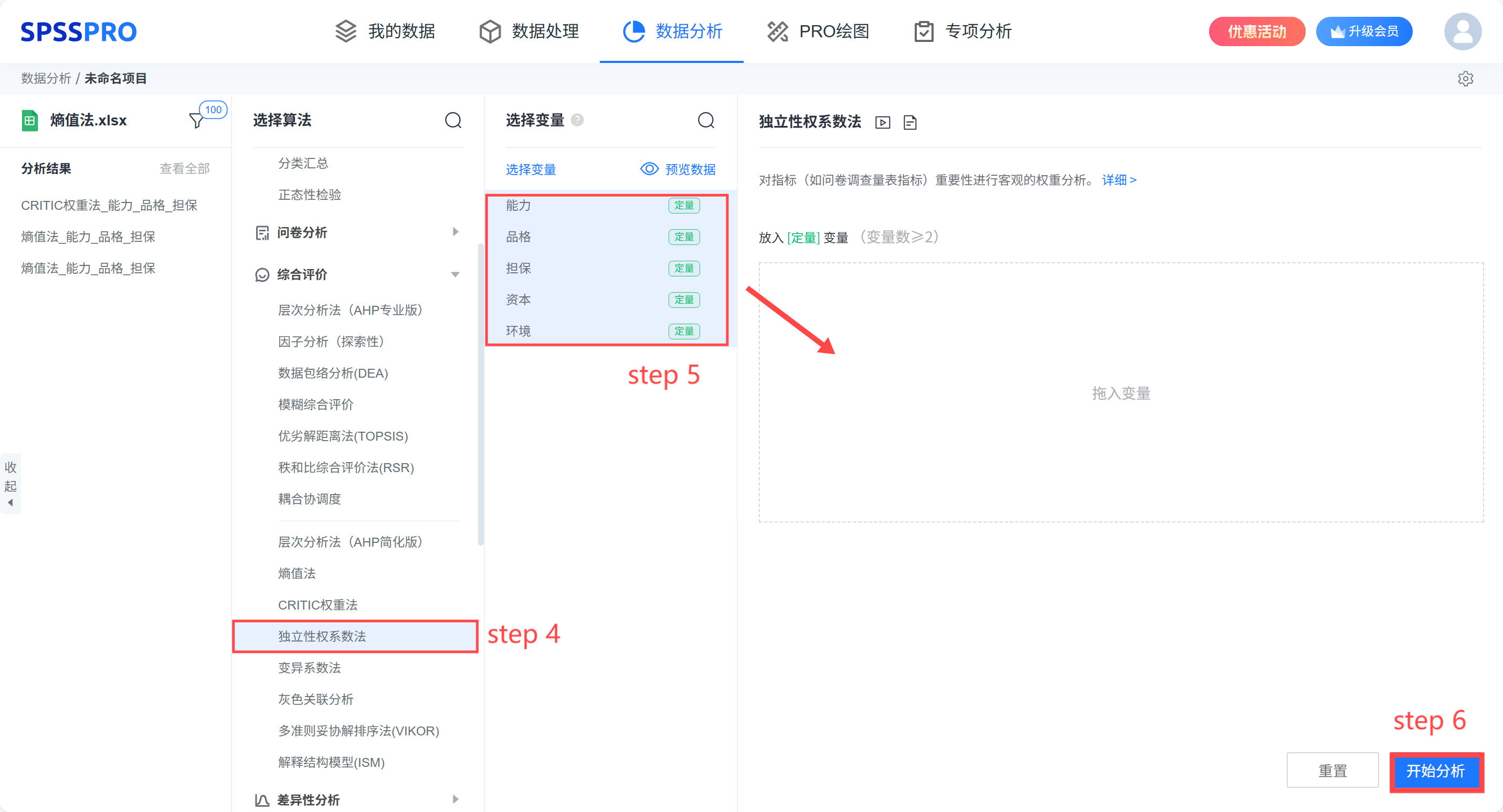

step4：选择【独立性权系数法】；
step5：查看对应的数据数据格式，【独立性权系数法】要求特征序列为定量变量，且至少有两项；
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：权重分析计算结果

项	复相关系数 R	复相关系数倒数 1/R	权重
能力	0.894	1.118	0.171
品格	0.894	1.119	0.171
担保	0.847	1.181	0.18
资本	0.836	1.197	0.183
环境	0.516	1.938	0.296

图表说明：独立性权系数法的权重计算结果显示，能力的权重为 17.066%、品格的权重为 17.073%、担保的权重为 18.018%、资本的权重为 18.265%、环境的权重为 29.577%，其中指标权重最大值为环境 （29.577%），最小值为能力 （17.066%）。

输出结果 2：指标重要度直方图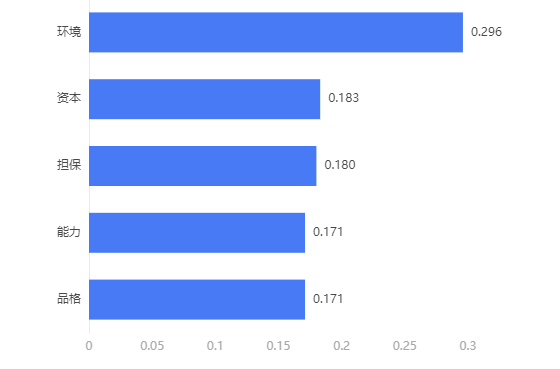

图表说明：上图以直方图形式展示了指标的重要度排序（降序）。

# 7、注意事项

• 若是各个指标之间的单位和量级(即计量指标的数量级)不同，在进行独立性权系数法前，需要对数据进行归一化，达到去量纲的目的。
• 独立性权系数法得到权重值后，此时归一化后数据与对应的权重相乘，并且进行累加，得到综合得分（需自行计算）。
• 独立性权系数法适应于三个及三个以上变量，若是只有两个变量，则负相关系数即为两个变量之间的相关系数，那么这两个变量的负相关系数不管怎样都是相同的，权重自然也相同，各 50%。

# 8、模型理论

独立性权系数法是根据各指标与其他指标之间的共线性强弱来确定指标权重的。
设有指标项 X1、X2、...... 、Xm，若指标 Xk 与其他指标的复相关系数越大，则说明与其他指标之间的共线性关系越强，越容易由其他指标的线性组合表示，重复信息越多，因此该指标的权重也就应该越小。
即若指标与其他指标的复相关系数 R 越大，该指标的权重越小。其中

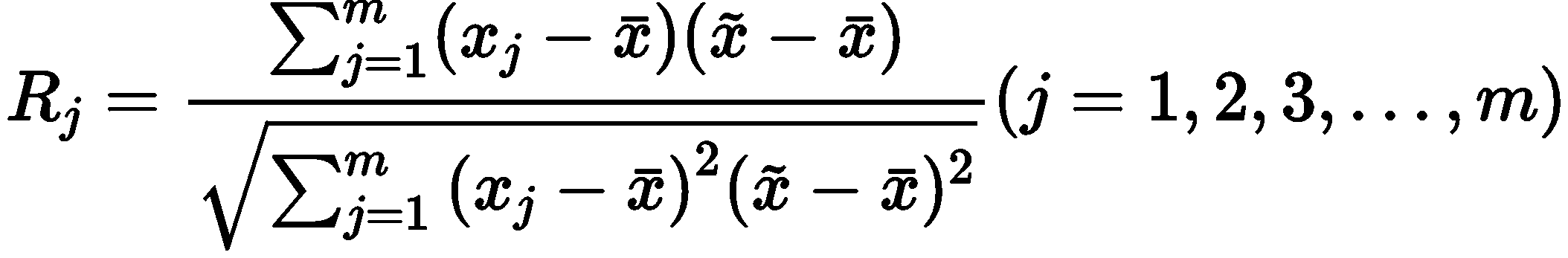
选取负相关系数的倒数，经过标准化处理计算得到最后的权重值:

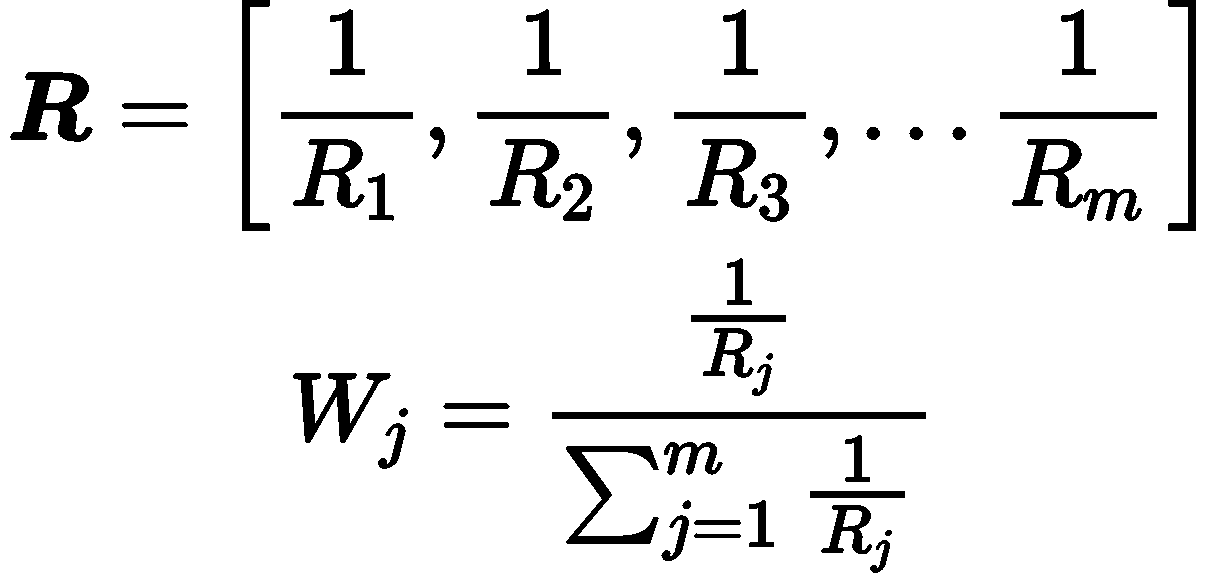
# 9、手推步骤

# Step 1：计算各指标的均值以及离均差：

均值：

离均差：

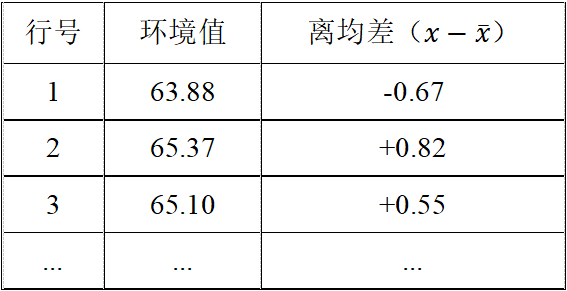
# Step 2：协方差矩阵计算

协方差公式：

$\text{Cov}(X,Y)=\frac{\sum (x_i-\overline{x})(y_i-\overline{y})}{n-1}$

示例：环境与能力的协方差
计算每行环境与能力的离均差乘积之和：

$\sum (x_{\text{环境}}-{\overline{x}}_{\text{环境}})(x_{\text{能力}}-{\overline{x}}_{\text{能力}})=-120.45$

协方差为：

$\text{Cov}(\text{环境, 能力})=\frac{-120.45}{99}\approx -1.217$

重复此过程，构建完整的协方差矩阵：

# Step 3:复相关系数 $R_j$ 计算（以环境为例）

复相关系数通过多元回归模型计算，公式为：

$R_j=\sqrt{\frac{\text{SSR}}{\text{SST}}}$

其中：

• SST（总平方和）:$\sum (y_i-\overline{y}{)}^2$
  
• SSR（回归平方和）:$\sum ({\hat{y}}_i-\overline{y}{)}^2$
  

构建正规方程: 使用协方差矩阵和均值，构建回归系数方程：

$\{\begin{array}{l}{b}_1\cdot \text{Cov}(X_1,X_1)+b_2\cdot \text{Cov}(X_1,X_2)+\cdots =\text{Cov}(X_1,Y)\\ b_1\cdot \text{Cov}(X_2,X_1)+b_2\cdot \text{Cov}(X_2,X_2)+\cdots =\text{Cov}(X_2,Y)\\ ⋮\end{array}$

代入环境作为因变量，能力、品格、担保、资本为自变量：

$\{\begin{array}{l}4.35b_1+1.82b_2+0.97b_3+2.11b_4=-1.22\\ 1.82b_1+5.13b_2+1.45b_3+1.89b_4=-0.85\\ 0.97b_1+1.45b_2+3.76b_3+1.02b_4=+0.62\\ 2.11b_1+1.89b_2+1.02b_3+4.58b_4=-0.93\end{array}$

求解回归系数: 通过高斯消元法或矩阵求逆手动解方程:

$b_1=-0.12,b_2=-0.08,b_3=+0.18,b_4=-0.10$

计算预测值 $\hat{y}$ 回归方程：

$\hat{y}={\overline{y}}_{\text{环境}}+b_1(x_{\text{能力}}-{\overline{x}}_{\text{能力}})+b_2(x_{\text{品格}}-{\overline{x}}_{\text{品格}})+\dots$

例 第1行预测值：

${\hat{y}}_1=64.55+(-0.12)(61.76-63.89)+(-0.08)(60.82-63.95)+0.18(62.72-64.21)+(-0.10)(61.39-63.97)\approx 63.90$

计算 $SST$ 和 $SSR$

• $SST$ :环境的离均差平方和：
  

  $\sum (y_i-\overline{y}{)}^2=6.24\times 99=617.76$

• $SSR$ :预测值离均差平方和：
  

  $\sum ({\hat{y}}_i-64.55{)}^2\approx 164.25$

• $R²$:
  

  $R^2=\frac{164.25}{617.76}\approx 0.266\Rightarrow R_j=\sqrt{0.266}\approx 0.516$

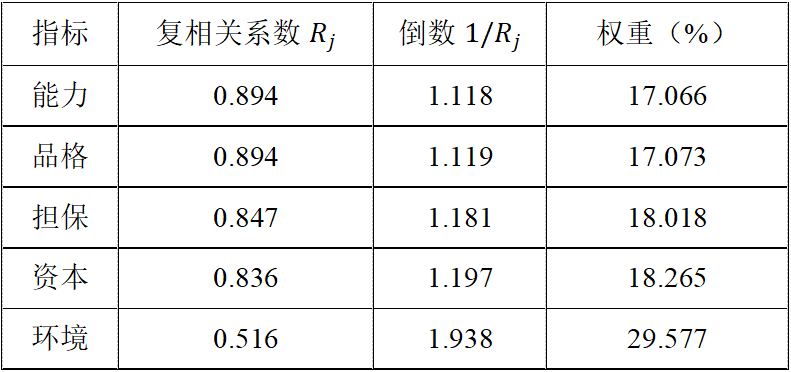
# Step 4:权重计算

复相关系数倒数:

$\frac{1}{R_j}=\frac{1}{0.516}\approx 1.938$

归一化权重:
总倒数之和：

$1.118(\text{能力})+1.119(\text{品格})+1.181(\text{担保})+1.197(\text{资本})+1.938(\text{环境})=6.553$

权重：

$W_{\text{环境}}=\frac{1.938}{6.553}\times 100\approx 29.577\mathrm{\%}$

最终计算结果如下：

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 张淑莹,胡友彪,邢世平. 基于独立性权-灰色关联度理论的突水水 源判别[J]. 水文地质工程地质 , 2018,45(6): 36-41+62.