层次分析法（AHP简化版）
# 1、作用
层次分析法是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法。该方法将定量分析与定性分析结合起来，用决策者的经验判断各衡量目标之间能否实现的标准之间的相对重要程度，例如通过构建评价指标（景色、费用，居住，饮食、旅途）对候选旅游地（桂林、黄山，北戴河）量化评价，进行选择。简化版里面，SPSSPRO 舍弃了对方案层的层次总排序，如需层次总排序，敬请期待 SPSSPRO-层次分析法（专业版）
# 2、输入输出描述
输入：根据提示进行指标或者方案两两对比
输出：各方案的量化得分或者同一级的指标权重
# 3、案例示例
案例：通过构建评价指标（景色、费用，居住，饮食、旅途）对候选旅游地（桂林、黄山，北戴河）量化评价，进行选择。（这里层次分析法简化版主要针对评价指标（景色、费用，居住，饮食、旅途）的权重建立分析）
# 4、案例数据
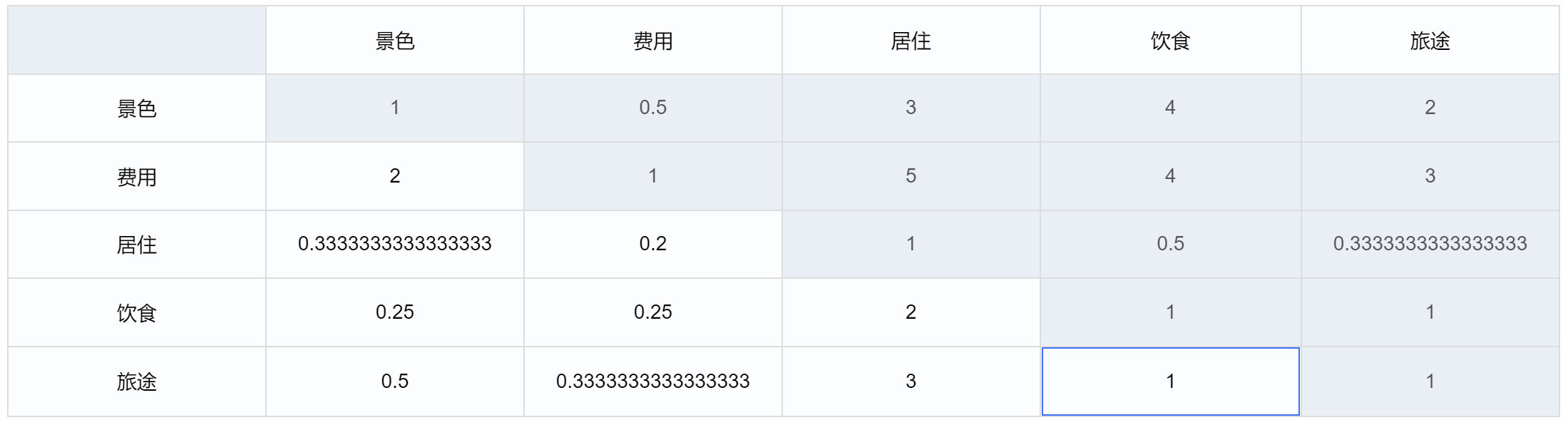
层次分析法案例数据
# 5、案例操作
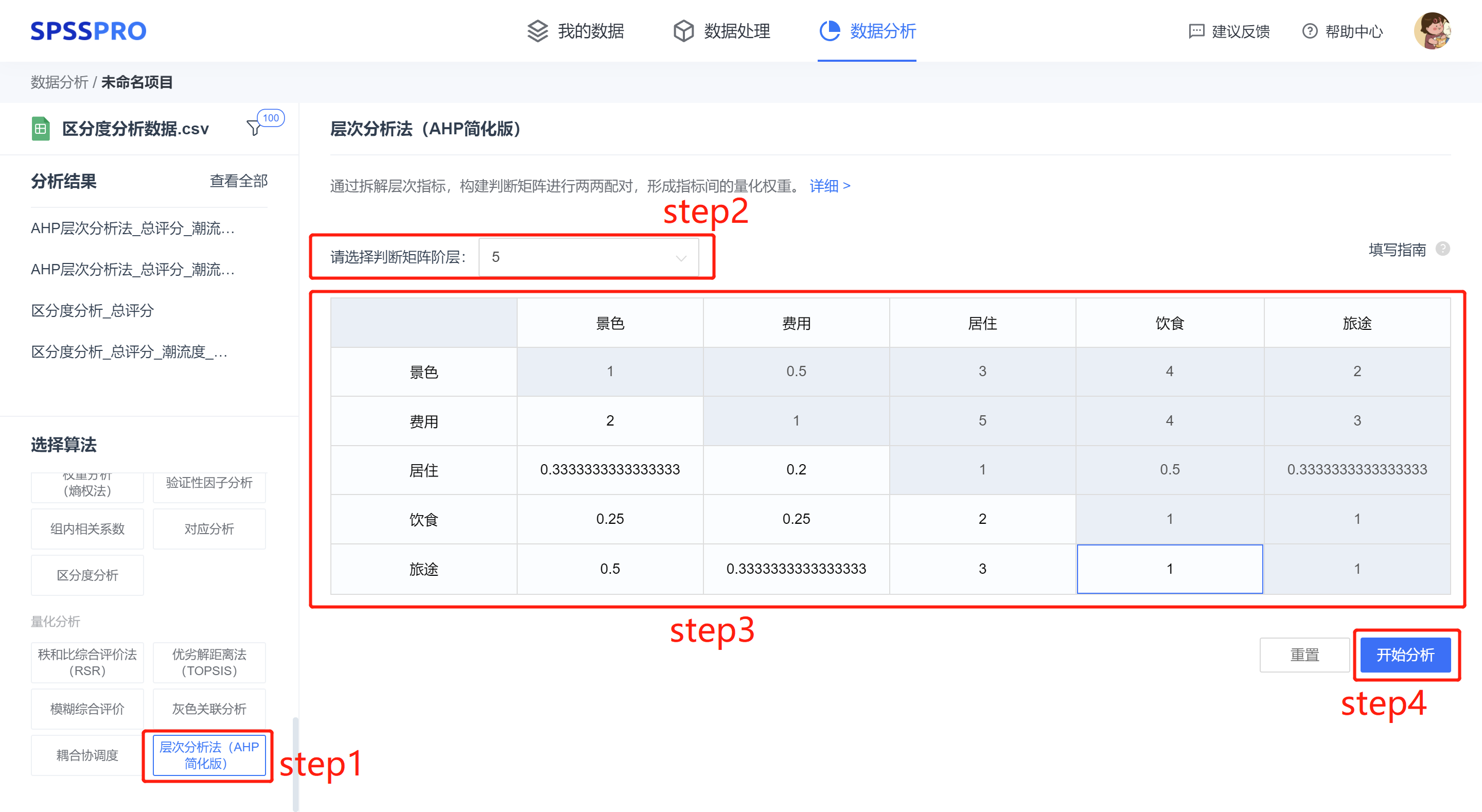step1：选择【层次分析法（AHP 简化版)】；（注意：在 spsspro 计算指标权重时用到的时方根法）
step2：选择判断矩阵阶层（注意：准则层有多少因素，那么判断矩阵阶层就是多少。在本例中，准则层包括景色、费用、居住、饮食、旅途，所以判断矩阵阶层是 5）
step3：设置判断矩阵（判断矩阵是对称矩阵），判断矩阵的元素 
表示的是第 
个因素相对于第 
个因素重要性比较结果，比如 a21=2，是指费用的重要性会比景色的重要性更大。
step4：点击【开始分析】，完成全部操作。
# 6、输出结果分析
层次分析法（AHP）分析结果
输出结果 1：指标指数
| 指标 | 景色 | 费用 | 居住 | 饮食 | 旅途 |
|---|---|---|---|---|---|
| 景色 | 1 | 0.5 | 3 | 4 | 2 |
| 费用 | 2 | 1 | 5 | 4 | 3 |
| 居住 | 0.3333 | 0.2 | 1 | 0.5 | 0.3333 |
| 饮食 | 0.25 | 0.25 | 2 | 1 | 1 |
| 旅途 | 0.5 | 0.3333 | 3 | 1 | 1 |
图表说明：上表显示了所构建的判断矩阵，如果超过 10 个指标，输出为预览前 10 个指标，全部数据请点击右上角下载按钮。
输出结果 2：AHP 层次分析结果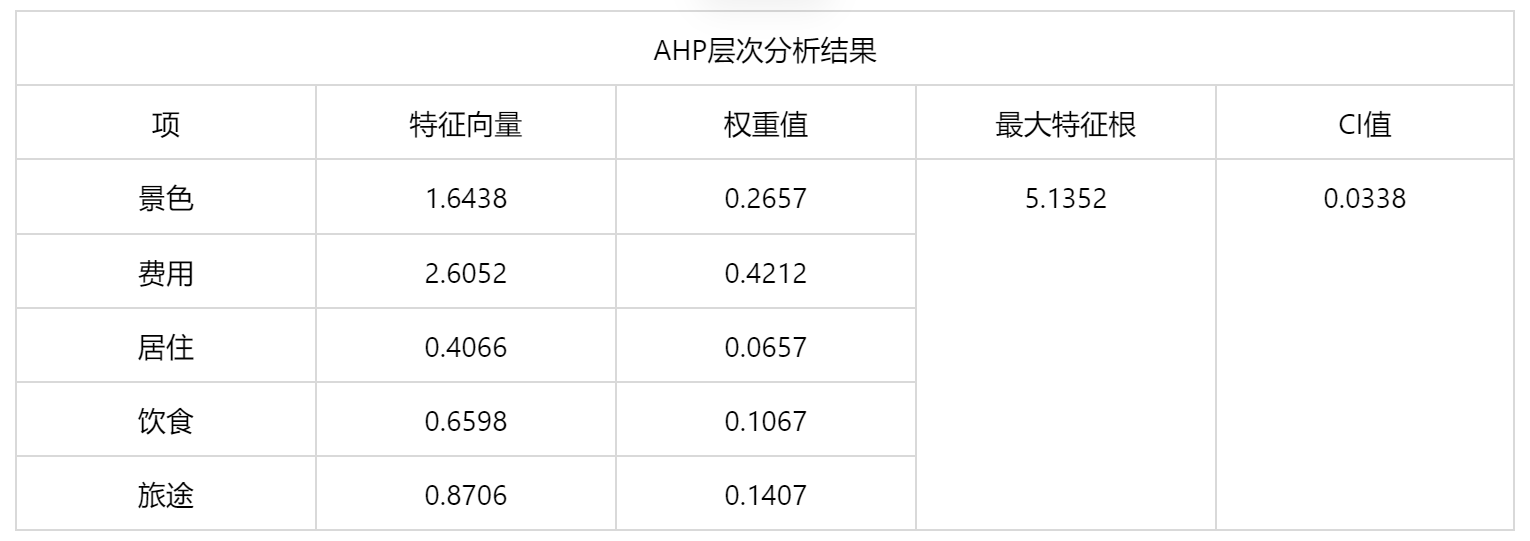 
图表说明：层次分析法(方根法)的权重计算结果显示，景色的权重得分为 0.2657，费用的权重得分为 0.4212，居住的权重得分为 0.0657，饮食的权重得分为 0.1067，旅途的权重得分为 0.1407。
输出结果 3：一致性检验结果
| 一致性检验结果 | ||||
|---|---|---|---|---|
| 最大特征根 | CI 值 | RI 值 | CR 值 | 一致性检验结果 |
| 5.1352 | 0.0338 | 1.11 | 0.0305 | 通过 |
图表说明：层次分析法的计算结果显示，最大特征根为 5.1352，根据 RI 表查到对应的 RI 值为 1.11，因此 CR=CI/RI=0.0305<0.1，通过一次性检验，说明该权重确定方法的合理性，否则需要对判断矩阵进行修改。
# 7、注意事项
- 一致性检验的含义用于确定构建的判断矩阵是否存在逻辑问题，例如以 A、B、C 构建判断矩阵，若判定 A 相当于 B 为 3（A 比 B 稍微重要），A 相当于 C 为 1/3（C 比 A 稍微重要），在判断 B 相当于 C 时，根据上述的逻辑，理应 C 比 B 重要，若我们在构建判断矩阵时，错误填写为 B 相当于 C 为 3（B 比 C 稍微重要），那么就犯了逻辑错误；
- 计算判断矩阵的特征向量有两种方式、分别为方根法与和法，SPSSPRO 默认采用方根法；
- RI 值采用近年来更受认可的 Franek and Kresta (2014)的方式，SPSSPRO 目前支持 15 阶。
# 8、模型理论
层次分析法的原理，层次分析法根据问题的性质和要达到的总目标，将问题分解为不同的组成因素，并按照因素间的相互关联影响以及隶属关系将因素按不同的层次聚集组合，形成一个多层次的分析结构模型，从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定。
其步骤为
（1）建立层次结构模型；
- 最高层(目标层)：决策的目的、要解决的问题；（本例中问题是选择旅游地）
- 中间层(准则层或指标层)：考虑的因素、决策的准则；（准则层是景色、费用、居住、饮食、旅途 5 各因素）
- 最低层(方案层)：决策时的备选方案；（方案层是我们决策的备选方案，即苏杭、北戴河、桂林三个旅游地）
（2）构造判断(成对比较)矩阵；
成对比较矩阵是表示本层所有因素针对上一层某一个*因素(准侧或目标)*的相对重要性的比较。成对比较矩阵的元素 
表示的是第 
个因素相对于第 
个因素的比较结果，这个值使用的是 Santy 的 1-9 标度方法给出。
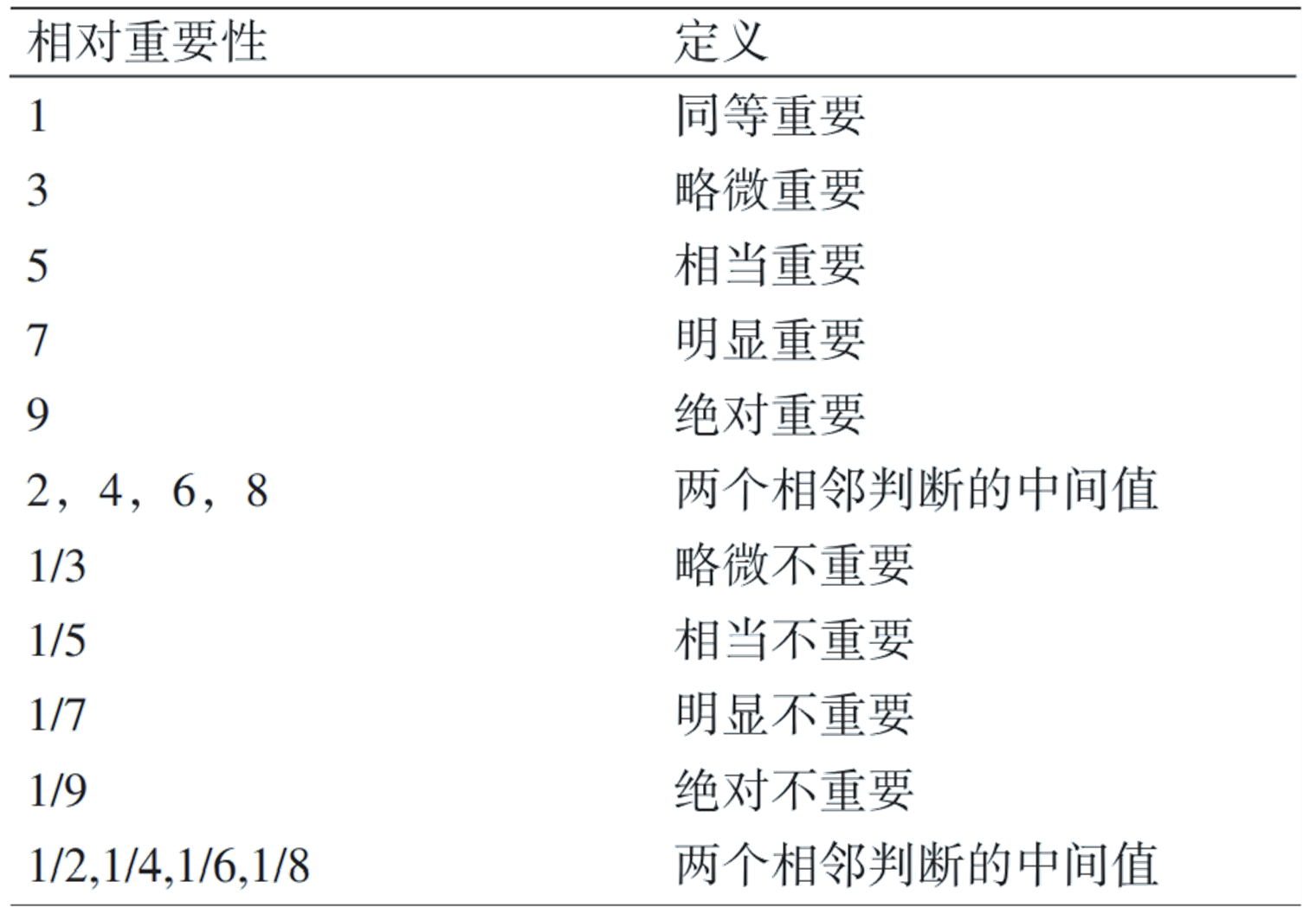
（3） 求解判断矩阵的特征向量。采用方根法计算矩阵特征向量的近似值 .
第一步：计算判断矩阵 A 每行元素乘积的 n 次方根，公式如下：
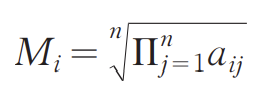
第二步：将 Mi 归 一化，公式如下：
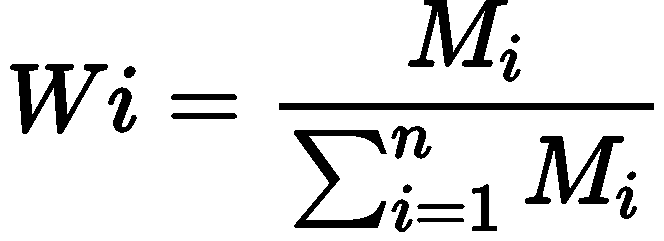
第三步：计算判断矩阵最大特征根
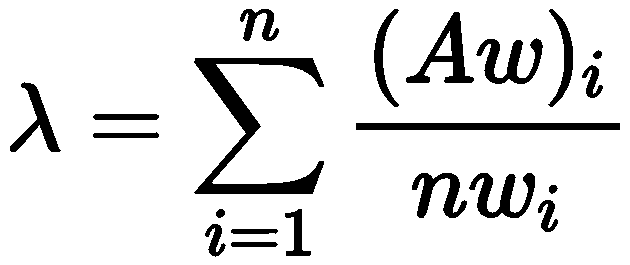
（4） 对判断矩阵的一致性进行检验。
CI 为度量判断矩阵偏离一致性指标，CI=(λ-n)/(n -1) ，CI 越大，判断矩阵 一致性越差，CI 为 0 时，判断矩阵具有完全一致性。
CR 为一致性比率，公式为：CR=CI/RI ，其中 RI 为平均随机一致性指标， 当 CR<0.1 时可以认为判断矩阵的一致性可以接受。
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]刘嘉周,王秀峰,苏剑楠,等. 基于层次分析法的健康中国建设指数研究[J]. 中国卫生经济,2021,40(5):56-60.
[3] Franek, J., Zmeškal, Z. 2013. A Model of Strategic Decision Making Using Decomposition SWOT-ANP Method. In: Financial Management of Firms and Financial Institutions 9th International Scientific Conference Proceedings (Part I-III). Ostrava: VŠB – Technical University of Ostrava, pp 172–180