层次分析法（AHP专业版）

操作视频

# 层次分析法（AHP专业版）

# 1、作用

层次分析法是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法。该方法将定量分析与定性分析结合起来，用决策者的经验判断各衡量目标之间能否实现的标准之间的相对重要程度，例如通过构建评价指标（景色、费用，居住，饮食、旅途）对候选旅游地（桂林、黄山，北戴河）量化评价，进行选择。在专业版里面，SPSSPRO 健全对方案层的层次总排序，如不需层次总排序，请选择 SPSSPRO-层次分析法（AHP 简化版）。

# 2、输入输出描述

输入：根据提示进行指标或者方案两两对比。
输出：各方案的量化得分或者同一级的指标权重。

# 3、案例示例

案例：通过构建评价指标（景色、费用，居住，饮食、旅途）对候选旅游地（桂林、黄山，北戴河）量化评价，进行选择。

# 4、案例操作

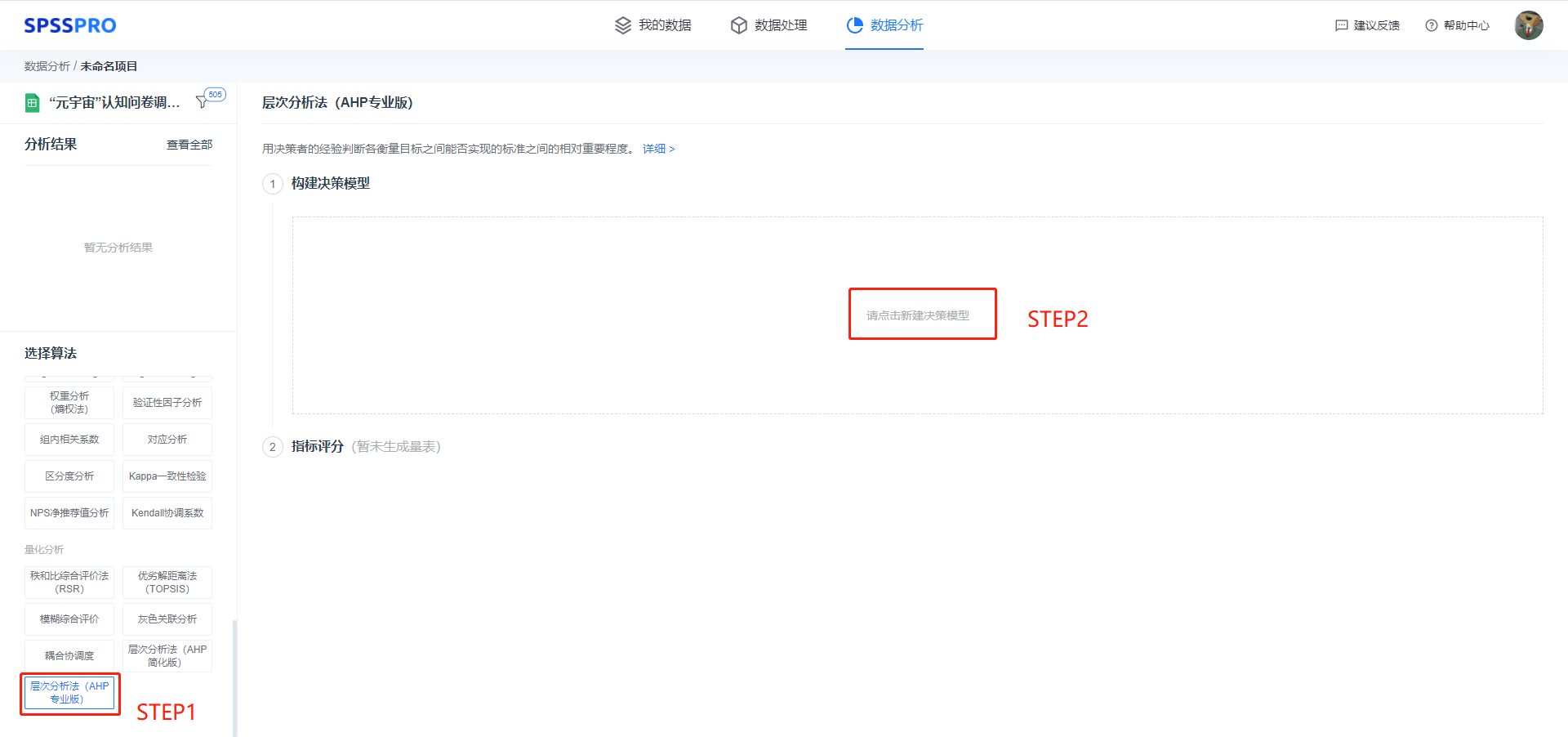
Step1：选择层次分析法（AHP 专业版）；
Step2：选择构建决策模型；

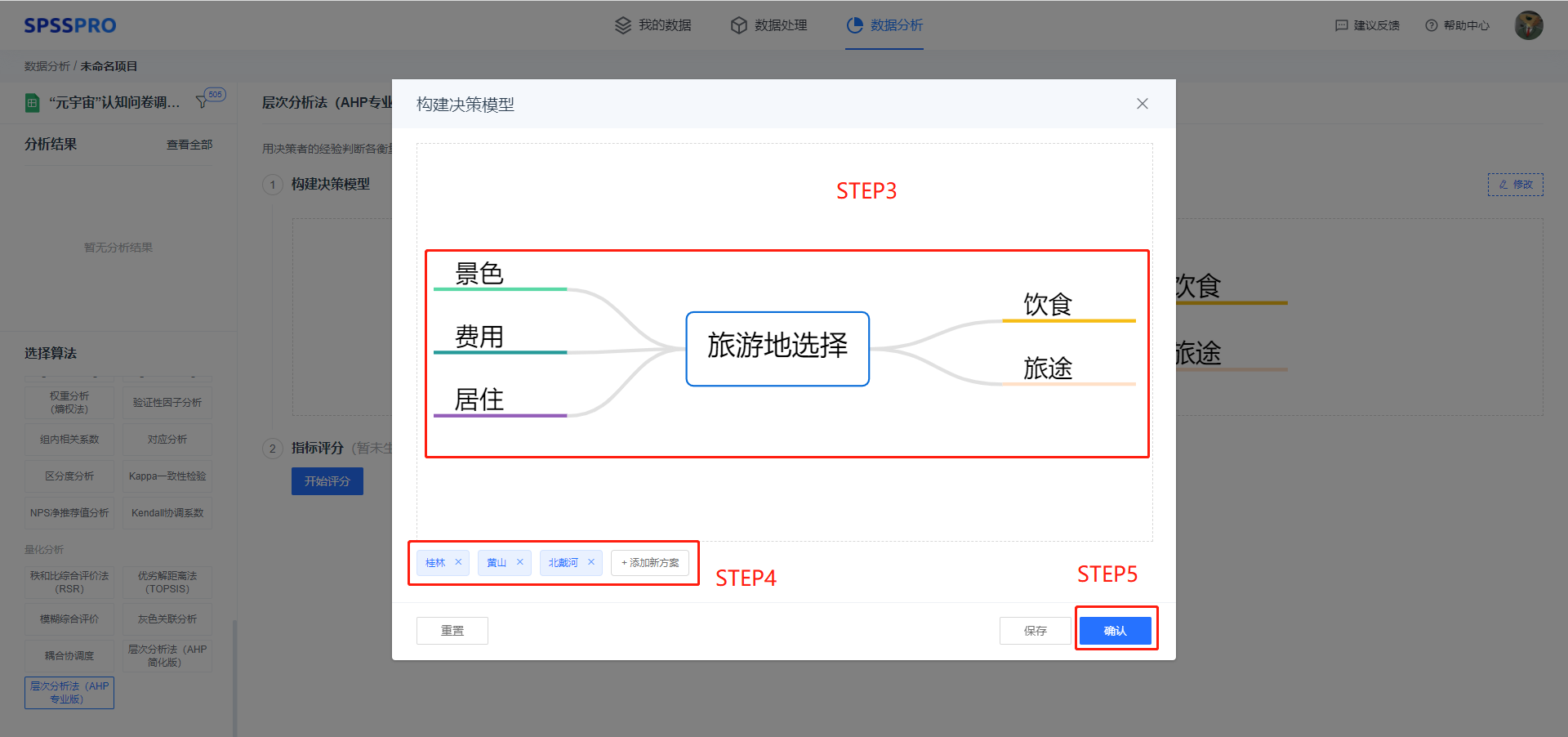
Step3：输入构建的评价指标；
Step4：输入最终的方案；
Step5：确认以进入下一步指标评分；

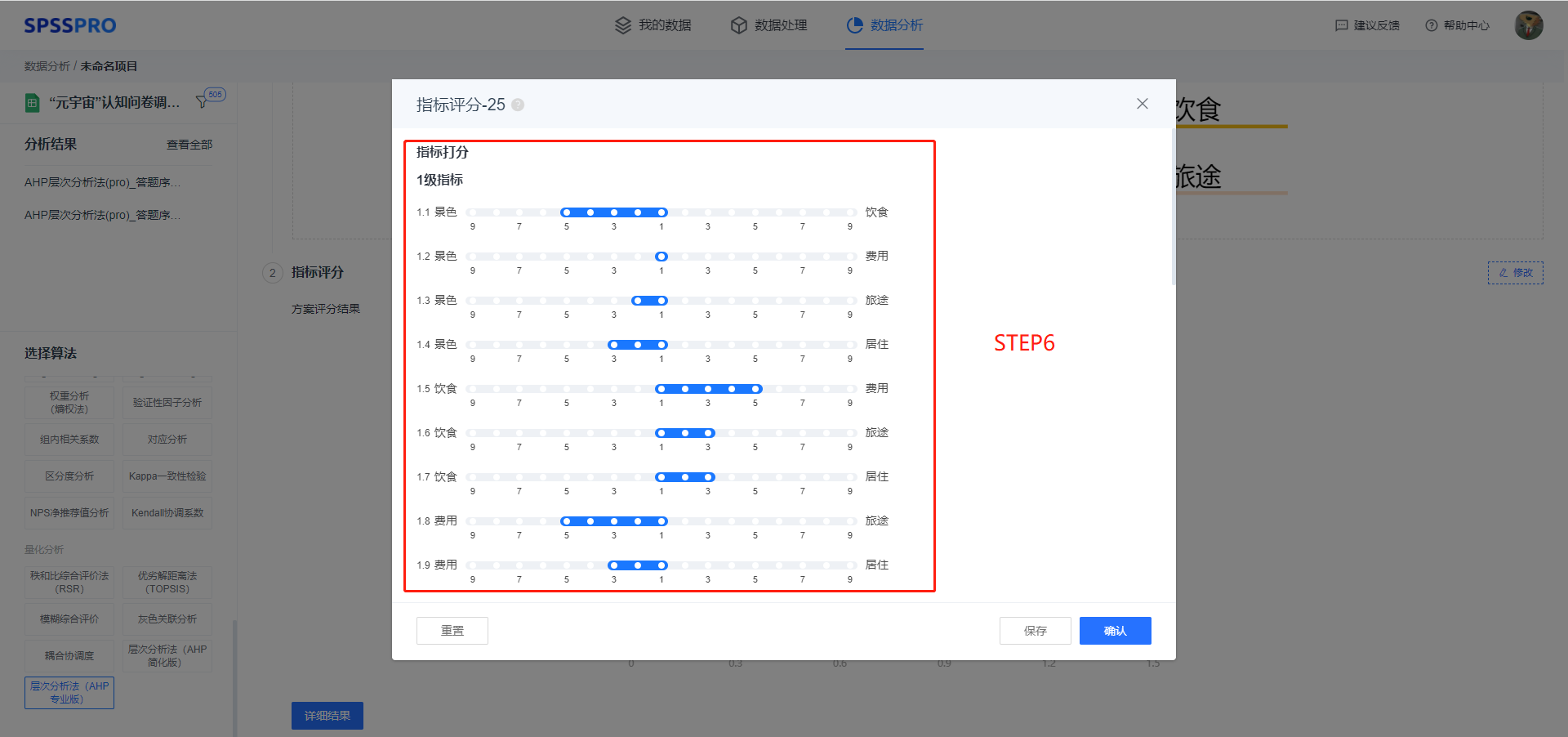
Step6：输入指标之间两两比对的重要程度值；

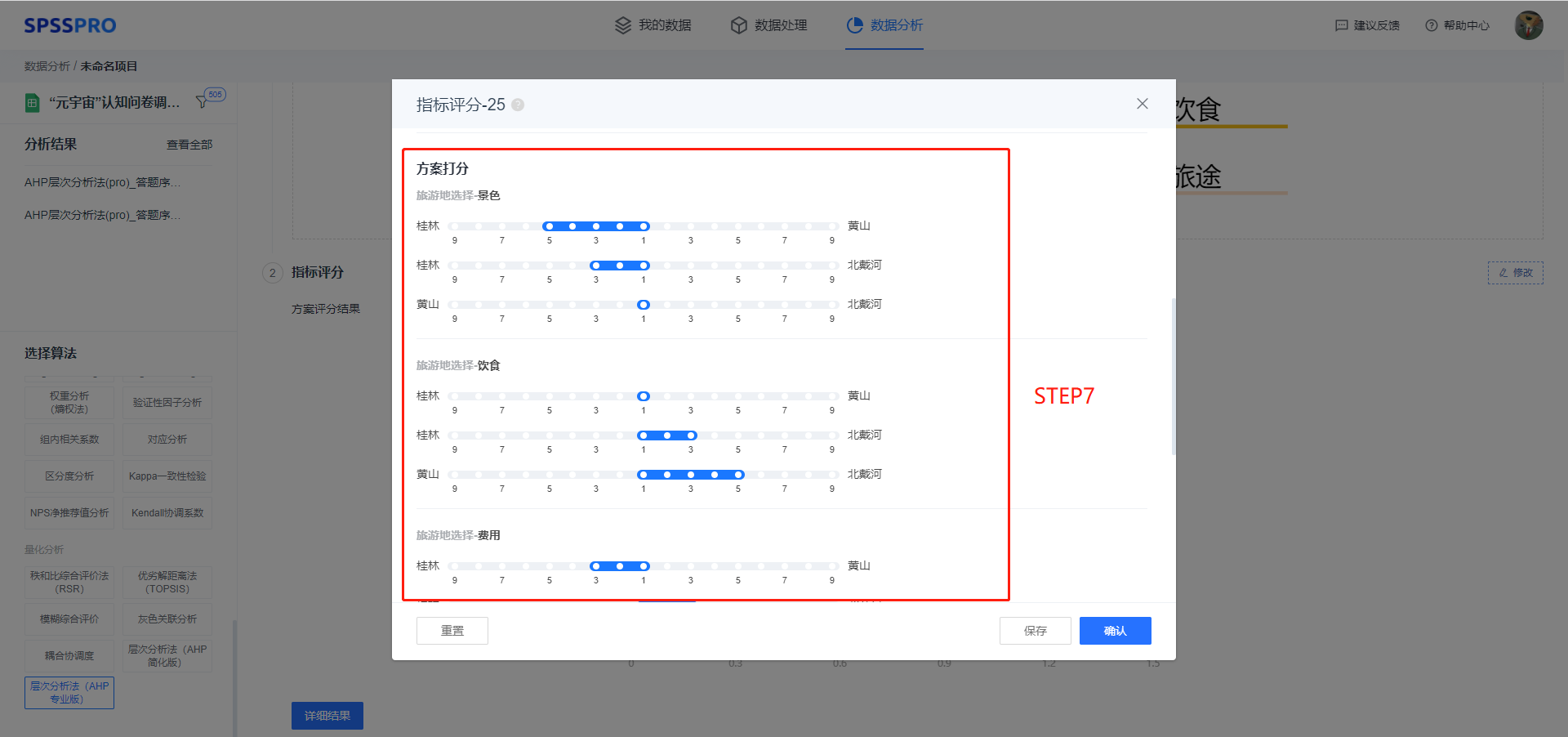
Step7：输入不同方案的对应评价值的重要程度评价。

# 5、输出结果分析

输出结果 1：方案得分

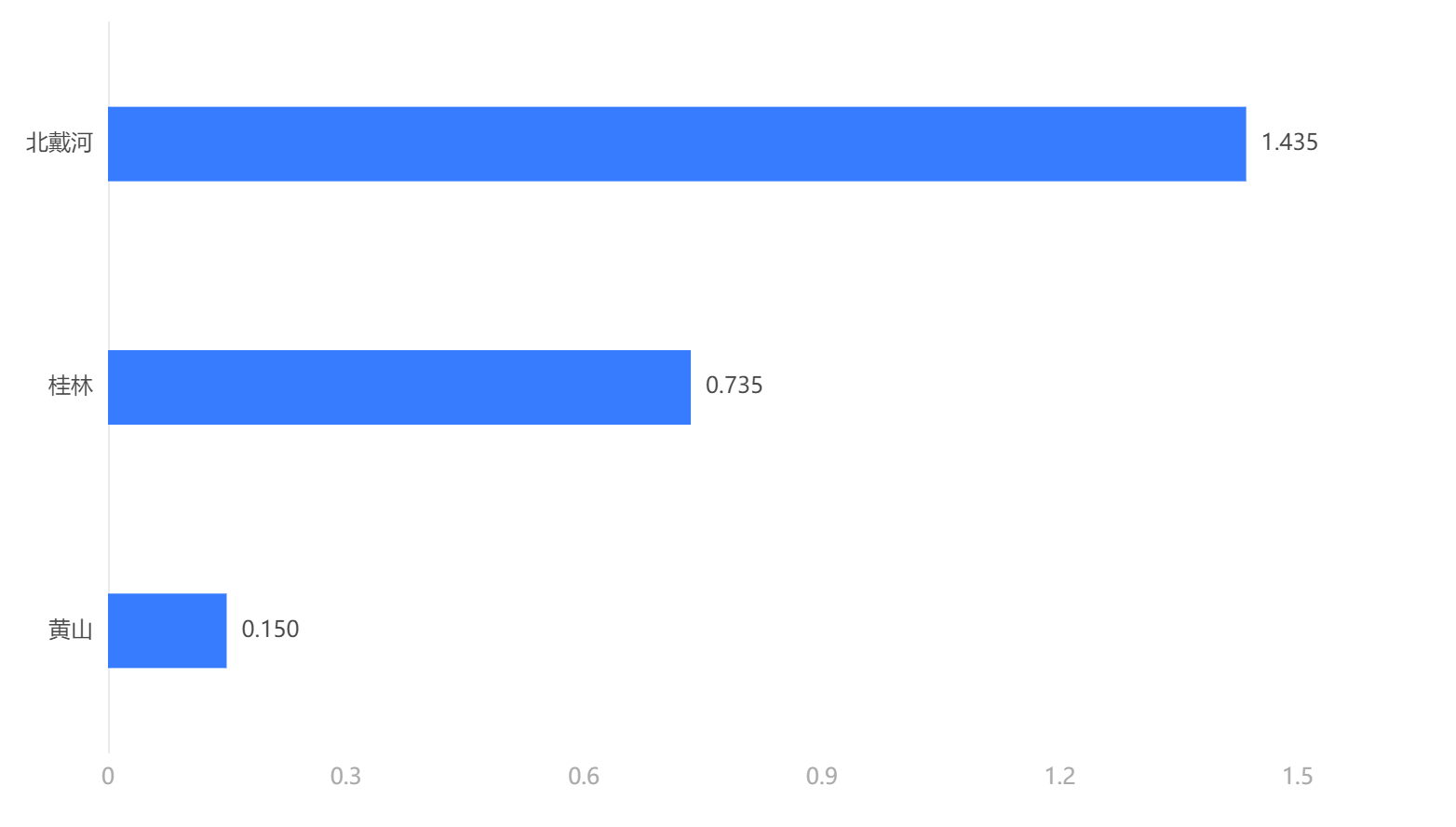
图表说明：计算某一层次所有因素对于最高层（总目标）相对重要性的权值，称为层次总排序，基于指标层次单排序与方案层次总排序后，对于旅游地选择最好的方案为北戴河、其次为桂林。
结果分析：北戴河的量化得分为 1.435，高过第二桂林近一倍。

输出结果 2：层次决策模型

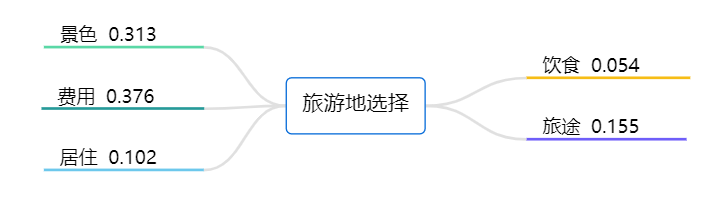
图表说明：一般的层次分析法会将决策的目标、考虑的因素（决策准则）和决策对象按照他们之间的相互关系分为最高层、中间层和最低层，绘出层次结构图。SPSSPRO 仅展示了决策的目标、考虑的因素（决策准则）以及各个因子对应的权重值。
结果分析：由图可见，其中最重要的两个决定因素是旅游地的景色和费用，而饮食、居住情况则属于低权重。

输出结果 3：判断矩阵汇总结果

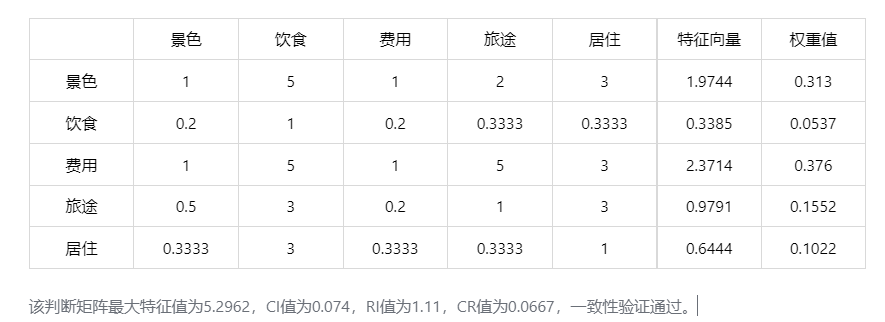
图表说明：上表展示了层次分析法的权重计算结果，根据结果对各个指标的权重进行分析，通过展示了一致性检验结果，用于判断是否存在构建判断矩阵的逻辑问题。
结果分析：CR 值小于 0.1，一致性检验通过，层次分析法结果有效。

输出结果 4：方案层判断矩阵汇总结果

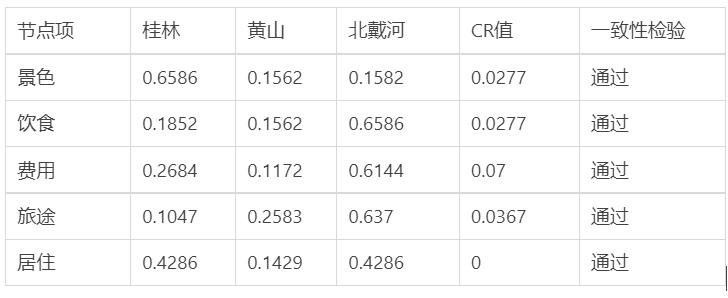
图表说明：上表展示了层次分析法的方案层的权重计算结果（即层次总排序），构建了个数为叶子节点指标的数目的判断矩阵对各个指标的权重进行分析，通过展示了一致性检验结果，用于判断方案层权重矩阵是否存在构建判断矩阵的逻辑问题。
结果分析：各项目一致性检验通过，层次分析法结果有效。

# 6、注意事项

设定判断矩阵时，可以使用德尔菲法，也可根据实际业务专家的建议来确定程度值。
层次总排序，该过程本为计算流程在最后一个步骤，为方便用户查看量化结果，SPSSPRO 预先置顶显示。
使用一致性检验判断所构建的判断矩阵是否存在逻辑错误，若不通过，则需重新构建判断矩阵。
计算判断矩阵的特征向量有两种方式、分别为方根法与和法，SPSSPRO 默认采用方根法；
RI 值采用近年来更受认可的 Franek and Kresta (2014)的方式，SPSSPRO 目前支持 15 阶。

# 7、模型理论

层次分析法（Analysis Hierarchy Process,简称 AHP），将人的思维过程分成目标层、准则层和方案层，并借助数学模型进行分析，是一种将决策者定性判断和定量计算有效结合起来的实用的决策分析方法。该方法系统性强，使用灵活、简便，适用于组织化的大规模复杂系统。尤其是当系统规模庞大、结构复杂、属性及目标多样，且系统中很多要素指标仅有定性关系时，采用层次分析法进行评价和决策是非常高效的。
基本原理是把复杂问题按支配关系分成递阶层次结构，每个层次都有相互联系相互作用的各个要素组成。通过逐对比较法对层次中各要素的相对重要性进行量化，最后进行相对重要性的总排序。
运用 AHP 法进行决策时，需要经历以下 4 个步骤：
1 建立多级递阶的结构模型
按支配关系自上而下分三层建立评价指标体系：
（1）最高层：也称目的层或目标层，是系统想要达到的目标或结果，是系统评价的首要准则。
（2）准则层：是为实现目标层所设立的准则、子准则等。
（3）最底层：也称方案层。是为实现目标所采取的各种方案、措施等。
2 构造两两比较判断矩阵
对同属一级的要素,以上一级的要素为准则进行逐对比较，建立判断矩阵。
采用两两成对比较,用 aij 表示要素 Bi 与要素 Bj 对目标 A 的影响程度之比：

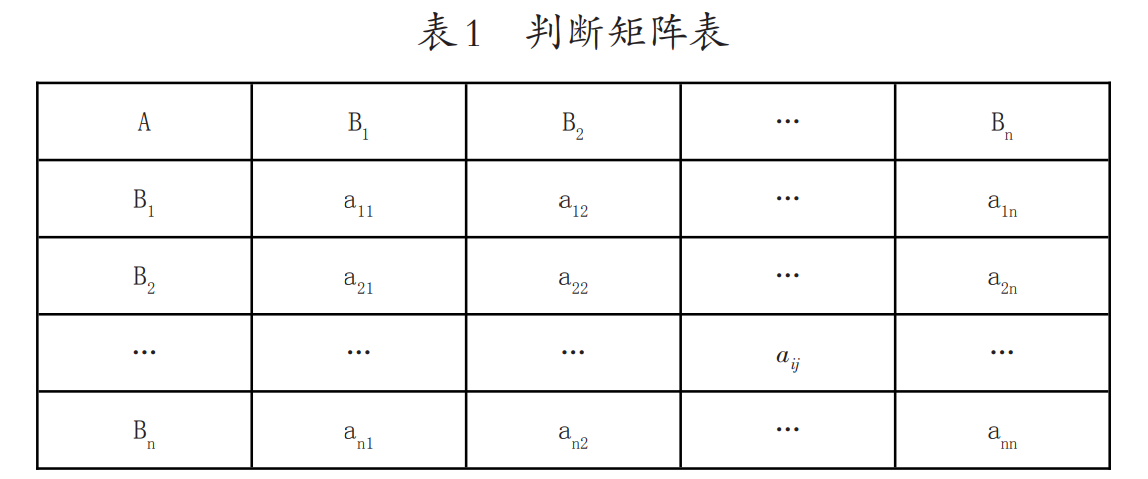
称矩阵 $A = (a_{i j})$ 为要素判断矩阵。判断矩阵 A 中的 i 元素与 j 元素相对重要度之比用 aij 表示,且有下述关系：

$a_{i j} \neq 0, a_{i j} = \frac{1}{a_{i j}}, a_{i j} = 1, i j = 1, 2, . . ., n$

比值越大，则 i 的重要度就越高。
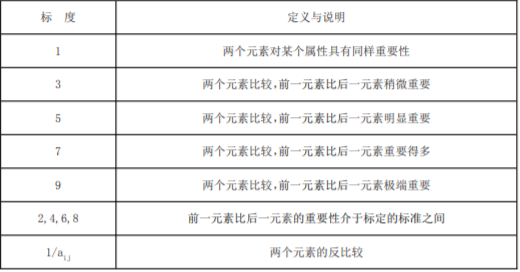
为了使判断定量化，根据 1-9 标度确定每个要素的相对重要度。

3 权重计算
（1）用求根法来计算判断矩阵特征向量的近似值。

$W_{i} = \frac{(\prod_{j = 1}^{n} a_{i j})^{\frac{1}{n}}}{\sum_{i = 1}^{n} (\prod_{j = 1}^{n} a_{i j})^{\frac{1}{n}}}, i j = 12 k n$

（2）把特征向量标准化后得到权重向量

W = (W_{1}, W_{2}, \dots, W_{n})^{T}

。
4 一致性检验
为保证求得的权重的正确性及合理性，还需要进行一致性检验。
计算一致性指标 C.I.

$C . I . = \frac{λ_{m a x} - n}{n - 1}$

其中，

$λ_{m a x} = \sum \frac{(A W)_{i}}{n W_{i}}$

显然，

n

越大，

C . I .

的误差越大。因此，在检验时引入随机性一致性比值

C . R .

$C . R . = \frac{C . I .}{C . R .}$

当随机一致性比率

C . R . < 0.1

时认为计算所得的层次排序权重是正确的、合理的，否则，需要重新调整判断矩阵，直到一致性检验合格为止。
5 综合重要度的计算
权重最大的方案即为实现目标的最优选择。

# 8、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 裴少婧,苏雅.层次分析法在高校教学评价体系中的应用研究[J].轻工科技,2021,37(04):167-169.

建议反馈