秩和比综合评价法(RSR)

操作视频

SPSSPRO教程-秩和比综合评价法(RSR)

# 秩和比综合评价法(RSR)

# 1、作用

秩和比（RSR）指将效益型指标从小到大排序进行排名、成本型指标从大到小排序进行排名，再计算秩和比，最后统计回归、分档排序。通过秩转换，获得无量纲统计量 RSR，以 RSR 值对评价对象的优劣直接排序或分档排序，从而对评价对象做出综合评价。

# 2、输入输出描述

输入:至少两项或以上的定量变量。
输出:反应考核指标在量化评价中的综合得分与分档

# 3、案例示例

案例:对某省 10 个地区的孕妇保健工作的三个指标进行综合评价

# 4、案例数据

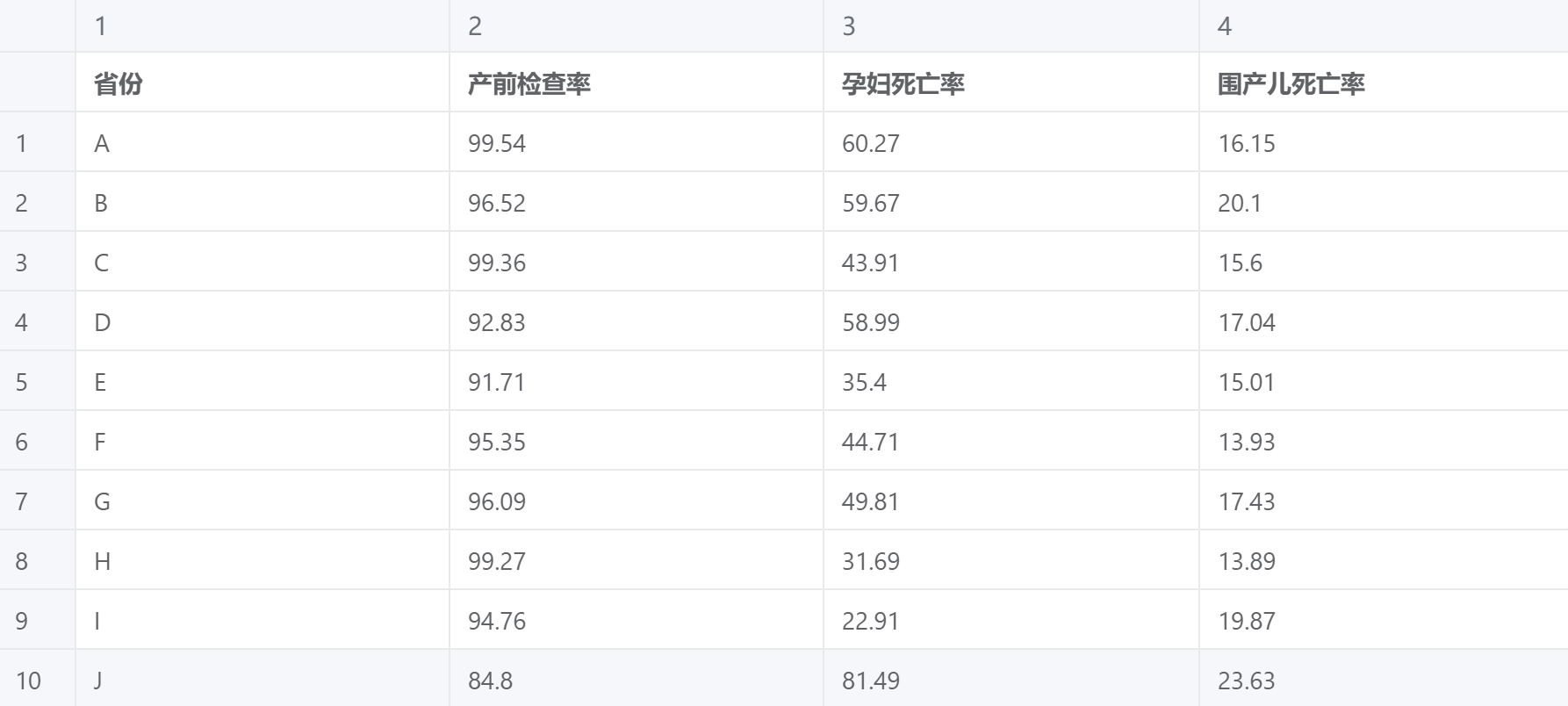
秩和比综合评价法(RSR)案例数据

# 5、案例操作

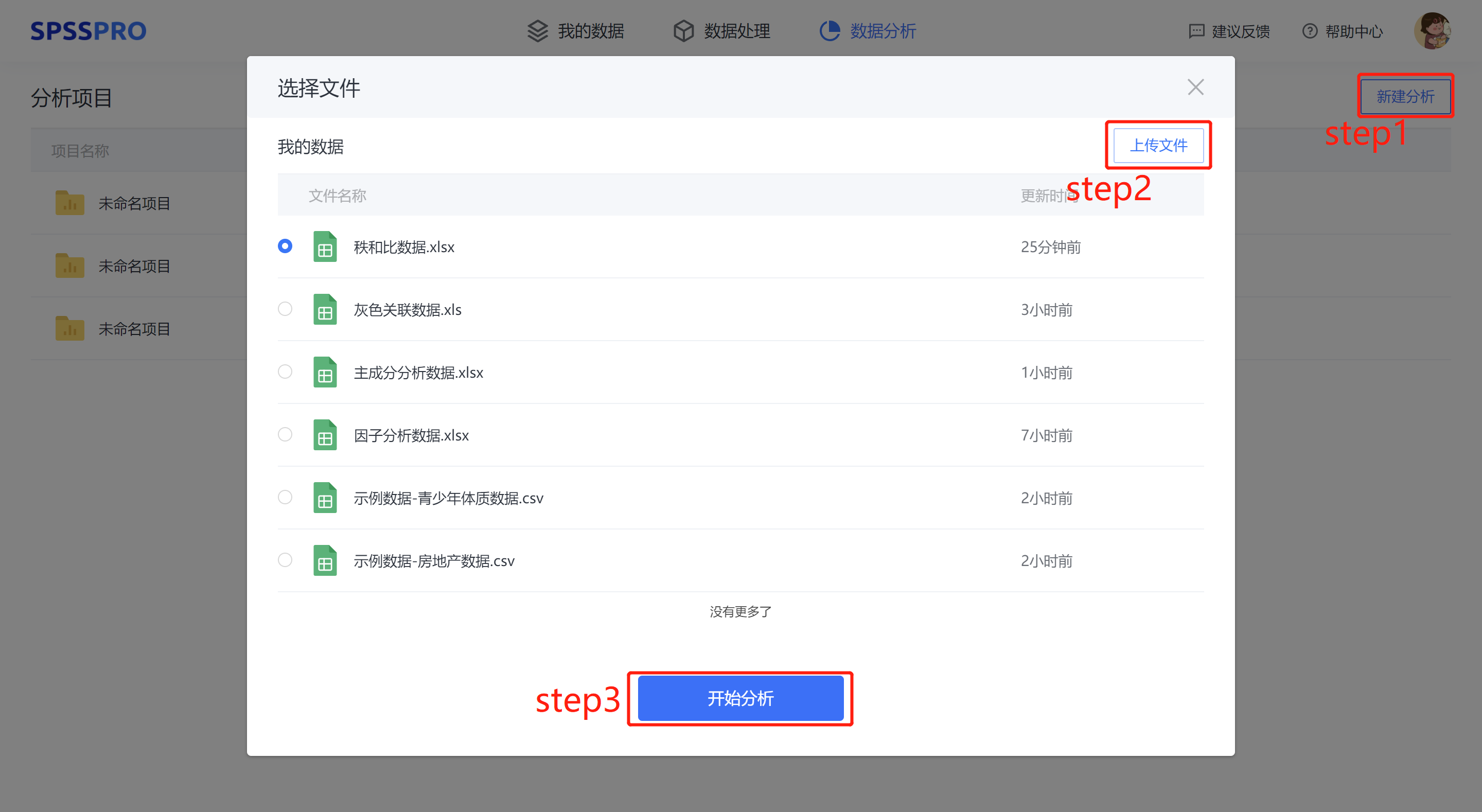
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；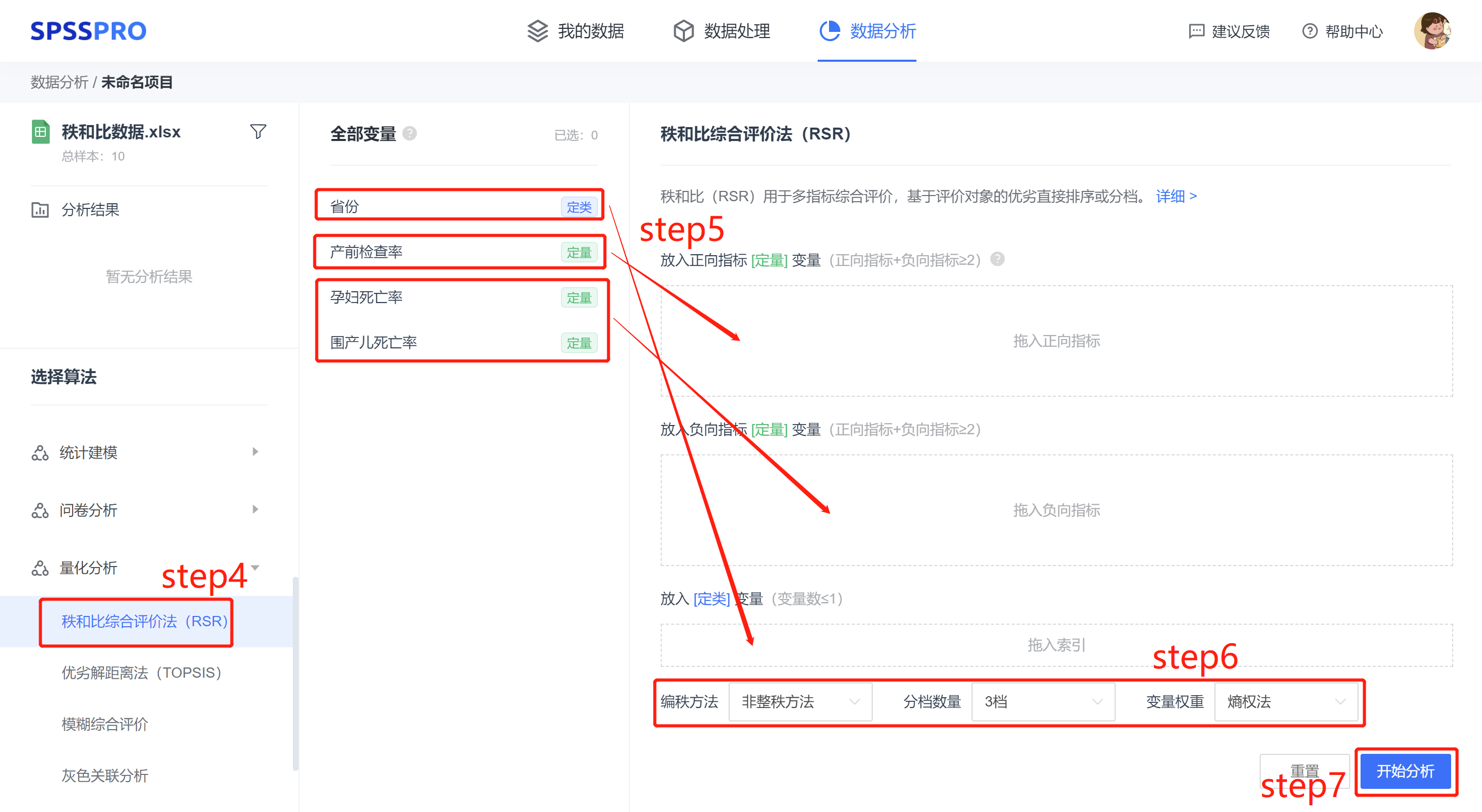

step4：选择【秩和比综合评价法】；
step5：查看对应的数据数据格式，【秩和比综合评价法】要求特征序列为定量变量，分为正向指标变量和负向指标变量，且正向指标变量和负向指标变量的个数之和大于等于两项。
step6：设置编秩方式（非整秩方法（推荐使用）、整秩方法、无处理）、分档数量（3 档、4 档、5 档）、变量权重（熵权法、不设置权重、自定义权重）。
step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：指标权重计算

图表说明:熵权法的权重计算结果显示，产前检查率的权重为 29.447%、孕妇死亡率的权重为 36.344%、围产儿死亡率的权重为 34.209%，其中指标权重最大值为孕妇死亡率（36.344%），最小值为产前检查率（29.447%）。

输出结果 2：秩值计算

索引	X1：产前检查率	R1：产前检查率	X2：孕妇死亡率	R2：孕妇死亡率	X3：围产儿死亡率	R3：围产儿死亡率	RSR	RSR_Rank
A	1.0000	9.9999	0.3622	4.2602	0.7680	7.9117	0.7200	6
B	0.7951	8.1560	0.3725	4.3523	0.3624	4.2618	0.5441	9
C	0.9878	9.8900	0.6415	6.7736	0.8244	8.4199	0.8254	2
D	0.5448	5.9030	0.3841	4.4568	0.6766	7.0893	0.5783	8
E	0.4688	5.2191	0.7868	8.0811	0.8850	8.9650	0.7541	4
F	0.7157	7.4416	0.6279	6.6507	0.9959	9.9629	0.8017	3
G	0.7659	7.8935	0.5408	5.8672	0.6365	6.7289	0.6759	7
H	0.9817	9.8351	0.8501	8.6511	1.0000	9.9999	0.9461	1
I	0.6757	7.0814	1.0000	10.0000	0.3860	4.4744	0.7250	5
J	0.0000	1.0001	0.0000	1.0000	0.0000	1.0001	0.1000	10

分析:X1、X2、X3 是对原始数据进行同向趋势归一化后的结果，R1、R2、R3 对原始数据进行非整秩编秩后的结果。

输出结果 3：RSR 分布表

索引	RSR	频率 f	累计频数 Σf	评价秩数	评价秩数/n*100%	Probit
J	0.1000055172818725	1	1	1	10	3.7184484344554
B	0.5441461206105431	1	2	2	20	4.158378766427086
D	0.5783215648353828	1	3	3	30	4.475599487291959
G	0.6758664494304739	1	4	4	40	4.7466528968642
A	0.7199517754575212	1	5	5	50	5
I	0.7250272188983746	1	6	6	60	5.2533471031358
E	0.7540695801074253	1	7	7	70	5.52440051270804
F	0.801670448882063	1	8	8	80	5.841621233572914
C	0.8254492707094204	1	9	9	90	6.2815515655446
H	0.946115322279421	1	10	10	97.5	6.959963984540054

图表说明：以上表格为目的是为了计算 Probit 值，Probit 值是根据百分数（评价秩数/n*100%）在“百分数与概率单位对照表”得到的。
● 将 RSR 值按照从小到大的顺序排列;
● 列出各组频数;
● 计算各组累计频数;
● 确定各组 RSR 的秩次 R 及平均秩次 R-;
● 计算向下累计频率 R- / n × 100 %，最后一项用( 1 − 1 / 4 n ) × 100 % 修正;
● 根据累计频率，查询“百分数与概率单位对照表”，求其所对应概率单位 Probit 值;
● 利用表格中的 RSR 分布值作为自变量，Probit 值作为因变量，进行线性回归，结果如下表格。
PS：详细的百分数与概率单位对照表：https://s0.spsspro.com/resources/images/百分数与概率单位对照表.png (opens new window)

输出结果 4：线性回归

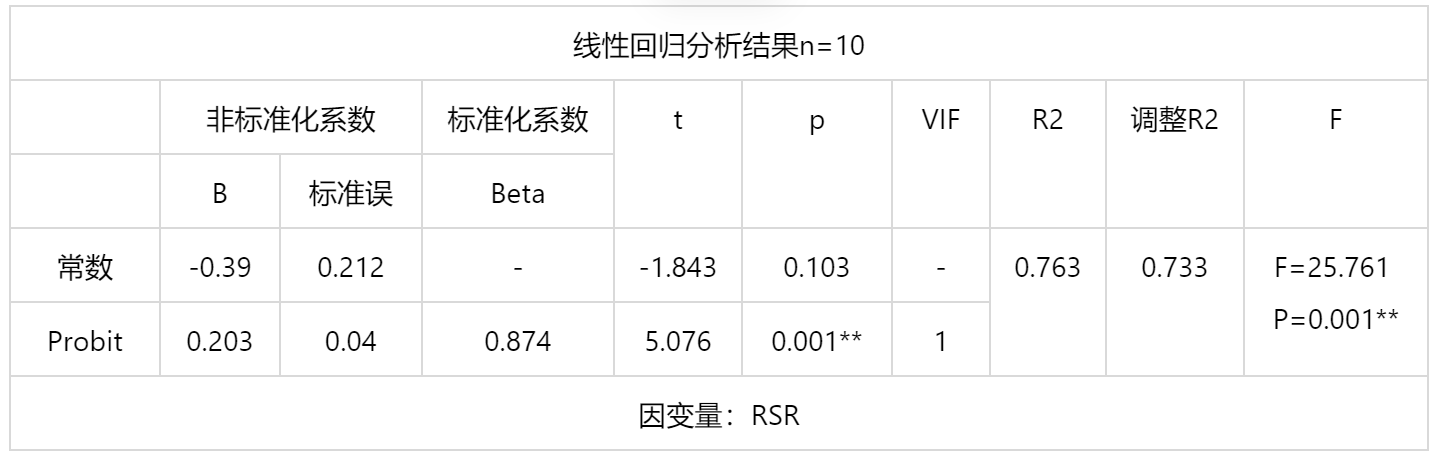
分析：以累计频率所对应的概率单位值 Probit 为自变量，以 RSR 值为因变量，计算回归方程。
从 F 检验的结果分析可以得到，显著性 P 值为 0.001，水平呈现显著性，拒绝了回归系数为 0 的原假设，同时模型的拟合优度 R² 为 0.763，模型表现较为良好，因此模型基本满足要求。对于变量共线性表现，VIF 全部小于 10，因此模型没有多重共线性问题，模型构建良好。对于变量共线性表现，VIF 全部小于 10，因此模型没有多重共线性问题，模型构建良好。
模型的公式如下： RSR=-0.39+0.203*Probit

输出结果 5：拟合效果图

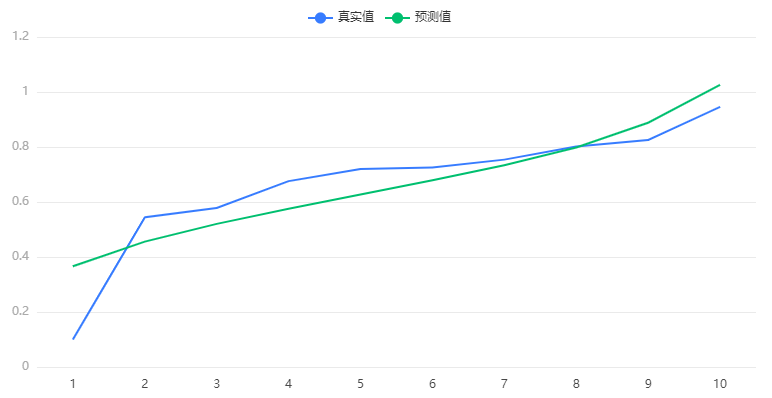
图表说明: 上图展示了本次模型的原始数据图、模型拟合值、模型预测值。

输出结果 6：分档排序临界值表格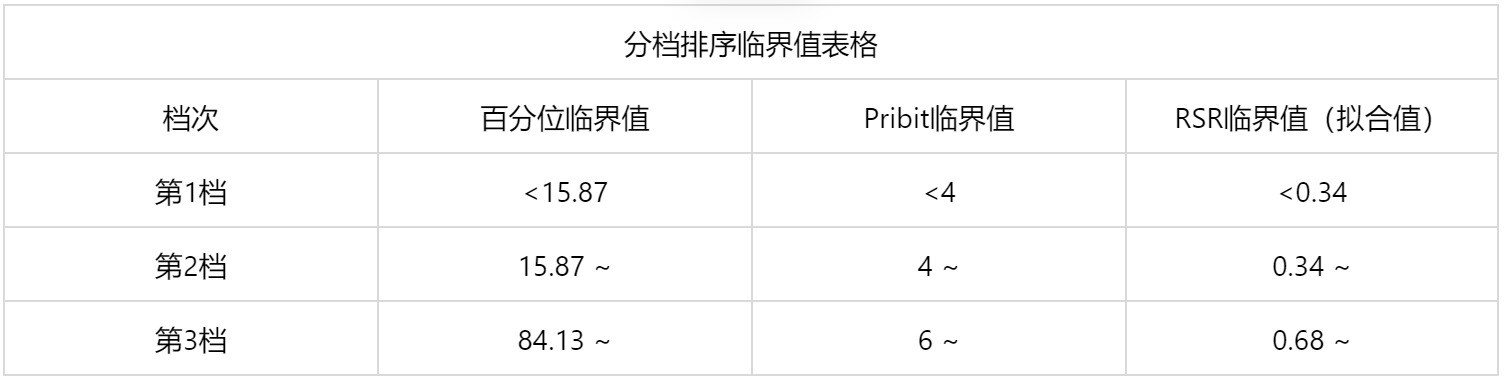

图表说明:本步骤目的在于得到分档排序临界值表格，尤其是 Probit 临界值对应的 RSR 临界值（拟合值）; 第一：百分位数临界值和 Probit 临界值根据分档水平数量而变化，该两项是固定值且完全一一对应; 第二：上表格中 RSR 临界(拟合值)是根据 Probit 临界值代入回归模型计算得到。

输出结果 7：分档等级结果汇总

索引	RSR_Rank	Probit	RSR Regression	Level
D	2	6.2815515655446	0.887928277115047	3
F	1	6.959963984540054	1.025957377925402	3
J	6	5	0.6271850989518994	2
B	9	4.158378766427086	0.4559496987141139	2
G	8	4.475599487291959	0.5204911039617149	2
A	4	5.52440051270804	0.7338790939420838	2
I	3	5.841621233572914	0.798420499189685	2
E	7	4.7466528968642	0.5756393550067596	2
C	5	5.2533471031358	0.6787308428970396	2
H	10	3.7184484344554	0.36644192078875193	1

图表说明:分档等级 Level 数字越大表示等级水平越高，即效应越好。由上表结果的三个分档等级可知，地区 D 和地区 F 的孕妇保健工作做的最好，而地区 H 的孕妇保健工作做的最差。

# 7、注意事项

如果在 SPSSPRO 中进行秩和比检验，且希望各指标有权重（如果不带权重则称 RSR，带权重则称 WRSR，RSR 是 WRSR 是一种特殊形式），可在输入页面的变量权重选择“自定义权重”处进行设置变量权重即可。

# 8、模型理论

RSR 法的基本思想是: 对评价指标排秩，以秩的平均值为评价标准，适用于对不同计量单位的指标进行综合评价。 RSR 法计算的基本步骤为:
（1）步骤 1 数据归一化+同趋势化
由于平台存在“正向指标”、“负向指标”，将分别对这两类数据做预处理。这里对最小值减去0.0001，对最大值加上0.0001是为了兼容一整列都为相同的值的情况，对整体结果影响不大，可忽略不计

$X_{m i n} = m i n (X_{1 j}, X_{2 j}, . . ., X_{n j}) - 0.0001$

$X_{m a x} = m a x (X_{1 j}, X_{2 j}, . . ., X_{n j}) + 0.0001$

对于正向指标：

$z_{i j} = \frac{X_{i j} - X_{m i n}}{X_{m a x} - X_{m i n}}$

对于负向指标：

$z_{i j} = \frac{X_{m a x} - X_{i j}}{X_{m a x} - X_{m i n}}$

（2）步骤 2 构造矩阵：假设评价对象为 n 个，评价指标为 m 个，构建数据矩阵 (n ×m）。

（3）步骤 3 编秩矩阵：
（3.1）整次秩和比法：将 n 个评价对象的 m 个评价指标排列成 n 行 m 列的原始数据表。编出每个指标各评价对象的秩，其中效益型指标从小到大编秩，成本型指标从大到小编秩，同一指标数据相同者编平均秩。得到秩矩阵，记

（3.2）非整次秩和比法：为了改进 RSR 法编秩方法的不足，所编秩次与原指标值之间存在定量的线性对应关系，从而克服了 RSR 法秩次化时易损失原指标值定量信息的缺点。
对于效益型指标：

对于成本型指标：

（4）步骤 4 计算秩和比：
权重相同时，

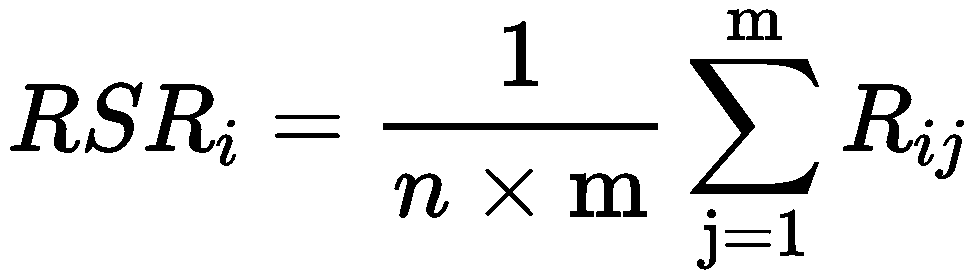
权重不同时，

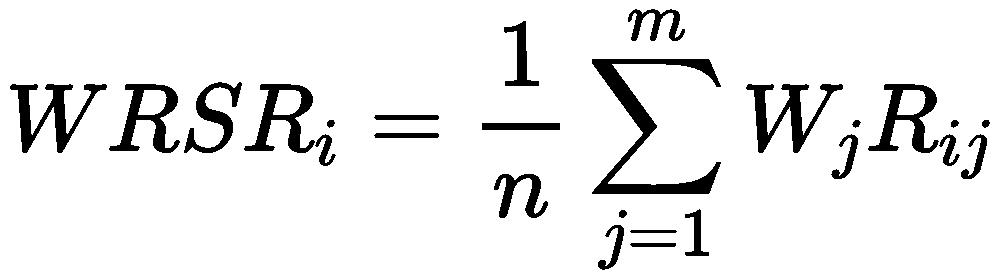
Rij 是第 i 个对象的第 j 个指标的秩，Wj 表示第 j 个指标的权重，权重和为 1。RSRi 的值越大，说明评价对象越优。

（5）步骤 5 计算概率单位
编秩得到 RSR(或 WRSR)频率分布表，列出各组频数 f，计算各组的累计频数 cf 和累计频率 p，将转换为概率单位 probit。

（6）步骤 6 计算直线回归方程
以 probit 值为自变量，以 RSR 为因变量，计算直线回归方程。

（7）步骤 7 分档排序，按照回归方程推算得到的 RSR（WRSR）估计值对评价对象进行分档排序。

# 9、手推步骤

Step 1：数据处理

先将数据同趋势处理后得到：

接下来对数据进行归一化处理，公式如下：

$z_{i j} = \frac{X_{i j} - min (X_{j})}{max (X_{j}) - min (X_{j})}$

示例计算：

产前检查率： $z_{A 1} = \frac{99.54 - 84.80}{99.54 84.80} = 1.0000$
孕妇死亡率: $z_{A 2} = \frac{21.22 - 0.00}{81.49 - 22.91} = \frac{21.22}{58.58} = 0.3622$
围产儿死亡率: $z_{A 3} = \frac{7.48 - 0.00}{23.63 - 13.89} = \frac{7.48}{9.74} = 0.7680$

完整归一化结果：

Step 2:非整秩编秩计算
计算公式：

$R_{i j} = 1 + (n - 1) \times z_{i j}, n = 10$

示例（A省）：

产前检查率: $R_{A 1} = 1 + 9 \times 1.0000 = 10.0000$
孕妇死亡率: $R_{A 2} = 1 + 9 \times 0.3622 = 4.2602$
围产儿死亡率： $R_{A 3} = 1 + 9 \times 0.7680 = 7.9120$

完整编秩结果：

Step 3:熵权法计算权重

1.计算归一化矩阵 $Z$ :

$Z_{i j} = \frac{z_{i j}}{\sum_{i = 1}^{10} z_{i j}}$

示例（孕妇死亡率列）：

$\sum z_{2} = 0.3622 + 0.3725 + \dots + 0.0000 = 5.524 Z_{A 2} = \frac{0.3622}{5.524} = 0.0656$

2.计算信息熵 $e_{j}$

$e_{j} = - \frac{1}{\ln (n)} \sum_{i = 1}^{n} Z_{i j} \ln (Z_{i j}), n = 10, \ln (10) \approx 2.3026$

示例（孕妇死亡率）:

$e_{2} = - \frac{1}{2.3026} (0.0656 \ln (0.0656) + \dots + 0.0000 \ln (1 e - 6)) \approx 0.928$

3.计算权重 $w_{j}$

$w_{j} = \frac{1 - e_{j}}{\sum_{j = 1}^{3} (1 - e_{j})}$

总信息效用值：

\sum (1 - e_{j}) = (1 - 0.942) + (1 - 0.928) + (1 - 0.932) = 0.198

权重计算： $w_{1} = \frac{0.058}{0.198} = 29.45 %, w_{2} = \frac{0.072}{0.198} = 36.34 %, w_{3} = \frac{0.068}{0.198} = 34.21 %$

Step 4：计算加权秩和比（WRSR）
公式：

$W R S R_{i} = \frac{1}{10} (w_{1} R_{i 1} + w_{2} R_{i 2} + w_{3} R_{i 3})$

示例（H省）

$W R S R_{H} = \frac{1}{10} (0.2945 \times 9.8351 + 0.3634 \times 8.6511 + 0.3421 \times 10.0000) \approx 0.9461$

以此类推计算，可得完整WRSR结果与排名：

Step 5：Probit分档与回归分析

1.计算累计频率与Probit值
将WRSR从小到大排列，计算累计频率 $p = \frac{R}{n} \times 100 %$ ，并查表转换为Probit值：

2.建立回归方程

最小二乘法计算回归系数:
公式:

$b = \frac{\sum (X_{i} - \bar{X}) (Y_{i} - \bar{Y})}{\sum (X_{i} - \bar{X})^{2}}, a = \bar{Y} - b \bar{X}$

其中,

\bar{X}

为Probit均值，

\bar{Y}

为WRSR均值。

计算过程：

计算均值：

$\bar{X} = \frac{3.7184 + 4.1584 + \dots + 6.9600}{10} = 5.2000$
$\bar{Y} = \frac{0.1000 + 0.5441 + \dots + 0.9461}{10} = 0.6666$
计算分子和分母:

$\sum (X_{i} - \bar{X}) (Y_{i} - \bar{Y}) = 5.6933$
$\sum (X_{i} - \bar{X})^{2} = 28.0716$
回归系数：

$b = \frac{5.6933}{28.0716} \approx 0.203$
$a = 0.6666 - 0.203 \times 5.2000 \approx - 0.39$

拟合优度 $R^{2}$ 的计算

$R^{2} = \frac{\sum ({\hat{Y}}_{i} - \bar{Y})^{2}}{\sum (Y_{i} - \bar{Y})^{2}}$
其中 ${\hat{Y}}_{i} = a + b X_{i}$ 为预测值。

计算结果: $R^{2} = 0.763$ ,表明模型解释了76.3%的WRSR变异，拟合效果较好。
以Probit为自变量，WRSR为因变量，拟合回归方程：

$WRSR = - 0.39 + 0.203 \times Probit (R^{2} = 0.763)$

示例（Probit=6.9600）:

$WRSR = - 0.39 + 0.203 \times 6.9600 \approx 0.9461$

3.确定分档临界值
根据Probit分位数：

第1档：WRSR < 0.4237
第2档：0.4237 ≤ WRSR < 0.8307
第3档：WRSR ≥ 0.8307

Step 6:最终分档结果

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 田凤调. 秩和比法及其应用[M]. 北京中国统计出版社,1993.
[3] 刘浩然,汤少梁. 基于 TOPSIS 法与秩和比法的江苏省基本医疗服务均等化水平研究[J]. 中国全科医学,2016,19(7):819-823. DOI:10.3969/j.issn.1007-9572.2016.07.017.

建议反馈