# 优劣解距离法（TOPSIS)

# 1、作用

TOPSIS 法是一种常用的组内综合评价方法，能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距。基本过程为基于归一化后的原始数据矩阵，采用余弦法找出有限方案中的最优方案和最劣方案，然后分别计算各评价对象与最优方案和最劣方案间的距离，获得各评价对象与最优方案的相对接近程度，以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格限制，数据计算简单易行。

# 2、输入输出描述

输入:至少两项或以上的定量变量。
输出:反应考核指标在量化评价中的综合得分。
​

# 3、案例示例

案例:为了客观地评价各风景地点的性价比，根据风景、人文、拥挤程度、票价等因素对各风景地点进行评估。

# 4、案例数据

优劣解距离法案例数据

# 5、案例操作

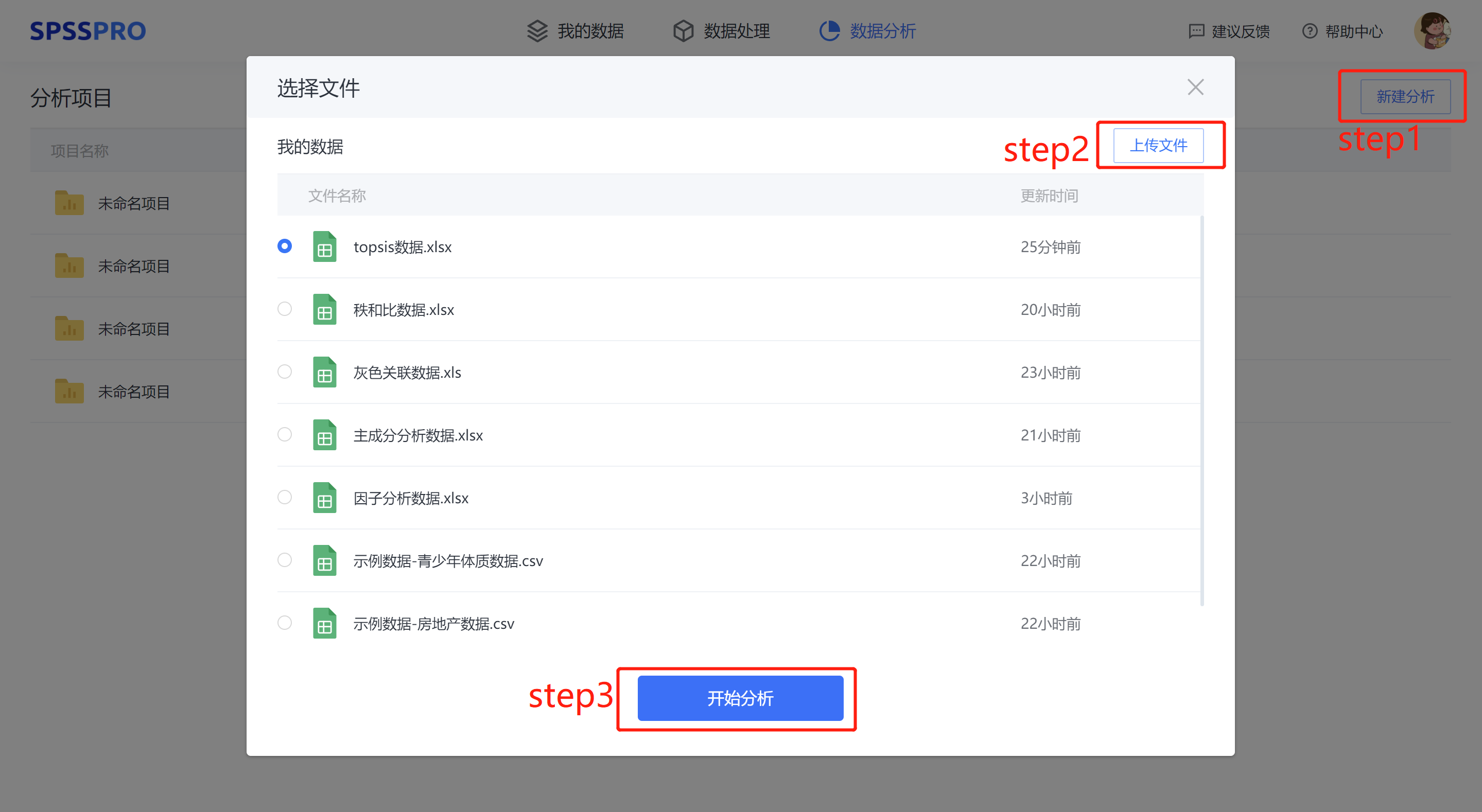
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；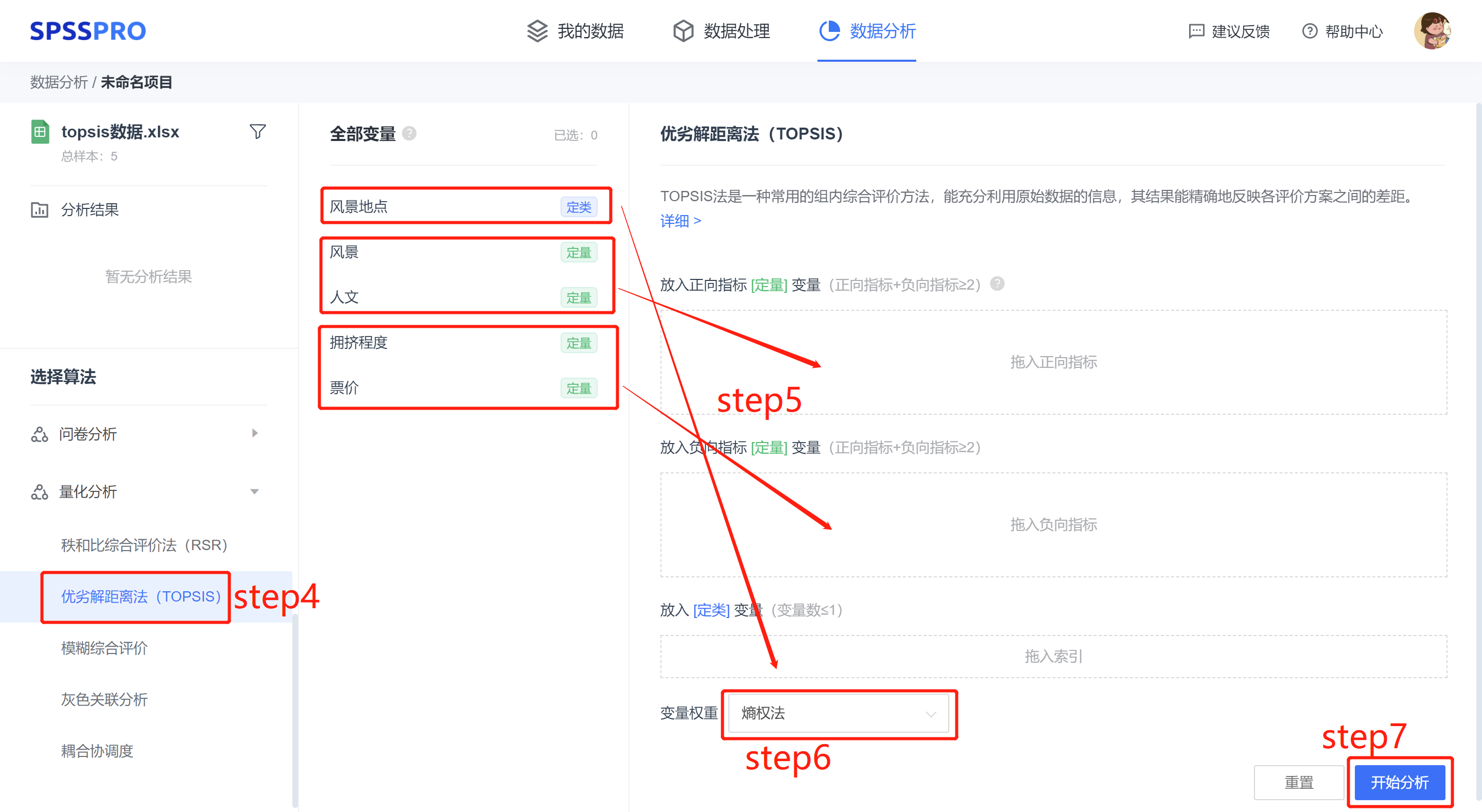

step4：选择【优劣解距离法（TOPSIS）】；
step5：查看对应的数据数据格式，【优劣解距离法（TOPSIS）】要求特征序列为定量变量，分为正向指标变量和负向指标变量，且正向指标变量和负向指标变量的个数之和大于等于两项。
step6：设置变量权重（熵权法、不设置权重）。
step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：指标权重计算 ​

图表说明：熵权法的权重计算结果显示，风景的权重为25.79%、人文的权重为22.684%、拥挤程度的权重为25.737%、票价的权重为25.79%，其中指标权重最大值为风景、票价（25.79%），最小值为人文（22.684%）。
​

输出结果 2：TOPSIS 评价法计算结果 ​

索引值	正理想解距离（D+）	负理想解距离（D-）	综合得分指数	排序
A	0.58864816	0.73970426	0.55685844	1
B	0.68956081	0.46675749	0.40365831	5
C	0.55297597	0.48326338	0.4663627	4
D	0.58134203	0.66059147	0.53190567	2
E	0.63882607	0.61200454	0.48927851	3

图表说明:由上表可知，景点 A 的综合评价最高，说明综合评估风景、人文、拥挤程度、票价后，景点 A 的性价比较高，距离负理想解相对远，距离正理想解相对近。
​

输出结果 3：中间值展示 ​

项	正理想解	负理想解
风景	1	0
人文	1	0
拥挤程度	1	0
票价	1	0

图表说明:表格给出的是正理想解（最优解）和负理想解（最劣解）的值。

# 7、注意事项 ​

• 进行 TOPSIS 分析时，各个指标有着权重属性（当然通常情况并没有），那么可对应设置各个指标的权重（输入的权重值可以为相对数字，SPSSPRO 默认都会进行归一化处理让权重加和为 1），在进行 D+和 D-值计算时，SPSSPRO 会对应乘上权重值（如果没有权重则下述公式中权重值为 1）；

# 8、模型理论

TOPSIS 法的基本思想是: 对原始数据同趋 势后构建归一化矩阵， 计算评价对象与最优向量和最劣向量的 差异， 以此测度评价对象的差异。 假设有 n 个评价对象，m 个 指标， TOPSIS 法的基本步骤为:
​
（1）步骤 1 ：原始数据正向化+同趋势化
由于平台存在“正向指标”、“负向指标”，将分别对这两类数据做预处理 。这里对最小值减去0.0001，对最大值加上0.0001是为了兼容一整列都为相同的值的情况，对整体结果影响不大，可忽略不计

$X_{min}=min(X_{1j},X_{2j},...,X_{nj})-0.0001$

$X_{max}=max(X_{1j},X_{2j},...,X_{nj})+0.0001$

对于正向指标：

$z_{ij}=\frac{X_{ij}-X_{min}}{X_{max}-X_{min}}$

对于负向指标：

$z_{ij}=\frac{X_{max}-X_{ij}}{X_{max}-X_{min}}$

​ （2）步骤2：计算最优解和最劣解

最优解：$（Z_1^{+}，Z_2^{+},...,Z_m^{+}）$
最劣解：$（Z_1^{-}，Z_2^{-},...,Z_m^{-}）$

（3）步骤 3 ：计算各评价指标与最优及最劣向量之间的差距

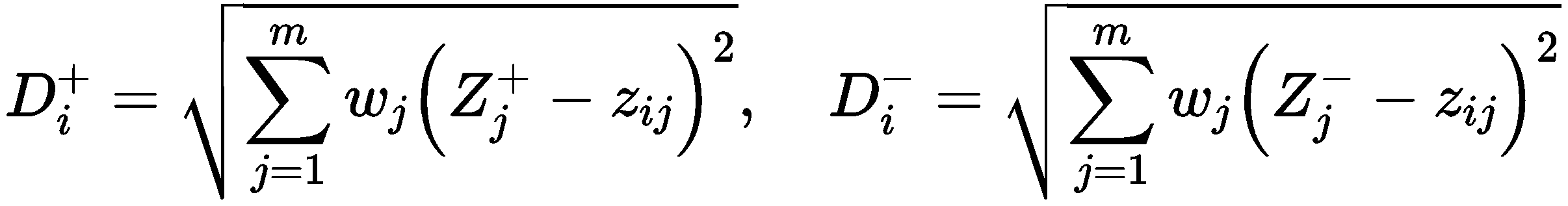
其中w_j为第 j 个属性的权重（重要程度）。

​（4）步骤 4 ：测度 评价对象与最优方案的接近程度

C_i 值越大， 表明评价对象越优

# 9、手推步骤

# Step 1：数据预处理：正向化与归一化

对正向指标，使用公式：

$z_{ij}=\frac{X_{ij}-X_{min}^j}{X_{max}^j-X_{min}^j}$

对负向指标，使用公式：

$z_{ij}=\frac{X_{max}^j-X_{ij}}{X_{max}^j-X_{min}^j}$

其中，为避免全列同值，对最小值减0.0001，最大值加0.0001：

$X_{min}^j=min(X_j)-0.0001,X_{max}^j=max(X_j)+0.0001$

计算过程：

1. 风景（正向指标）：
   $X_{min}=4-0.0001=3.9999$, $X_{max}=8+0.0001=8.0001$
   $\begin{array}{rl}{z}_{A1}& =\frac{4-3.9999}{8.0001-3.9999}\approx 0.000025,\\ z_{B1}& =\frac{7-3.9999}{4.0002}\approx 0.75,\\ z_{C1}& \approx 0.25,z_{D1}\approx 0.5,z_{E1}\approx 0.999975.\end{array}$

2. 人文（正向指标）：
   $X_{min}=2-0.0001=1.9999$, $X_{max}=10+0.0001=10.0001$
   $\begin{array}{rl}{z}_{A2}& =\frac{5-1.9999}{8.0002}\approx 0.375,\\ z_{B2}& \approx 0.5,z_{C2}\approx 0.625,z_{D2}\approx 0.9999875,z_{E2}\approx 0.0000125.\end{array}$

3. 拥挤程度（负向指标）：
   $X_{min}=2-0.0001=1.9999$, $X_{max}=10+0.0001=10.0001$
   $\begin{array}{rl}{z}_{A3}& =\frac{10.0001-2}{8.0002}\approx 0.9999875,\\ z_{B3}& \approx 0.25,z_{C3}\approx 0.5,z_{D3}\approx 0.0000125,z_{E3}\approx 0.625.\end{array}$

4. 票价（负向指标）：
   $X_{min}=30-0.0001=29.9999$, $X_{max}=50+0.0001=50.0001$
   $\begin{array}{rl}{z}_{A4}& =\frac{50.0001-30}{20.0002}\approx 0.999995,\\ z_{B4}& \approx 0.000005,z_{C4}\approx 0.5,z_{D4}\approx 0.75,z_{E4}\approx 0.25.\end{array}$

归一化矩阵：

风景地点	风景($z_1$)	人文($z_2$)	拥挤程度($z_3$)	票价($z_4$)
A	0.000025	0.375	0.9999875	0.999995
B	0.75	0.5	0.2500025	0.000005
C	0.25	0.625	0.5000025	0.5
D	0.5	0.9999875	0.0000125	0.75
E	0.999975	0.0000125	0.625	0.25

# Step 2：确定指标权重（熵权法）

计算指标概率矩阵 $p_{ij}$ $p_{ij}=\frac{x_{ij}}{\sum _{i=1}^n{x}_{ij}},\text{其中}{x}_{ij}\text{为正向化后数据}$

1. 风景（sum=30）：
   $\begin{array}{rl}{p}_{A1}& =4/30\approx 0.1333,p_{B1}=7/30\approx 0.2333,p_{C1}=5/30\approx 0.1667,\\ p_{D1}& =6/30=0.2,p_{E1}=8/30\approx 0.2667.\end{array}$

2. 人文（sum=30）：
   $\begin{array}{rl}{p}_{A2}& =5/30\approx 0.1667,p_{B2}=6/30=0.2,p_{C2}=7/30\approx 0.2333,\\ p_{D2}& =10/30\approx 0.3333,p_{E2}=2/30\approx 0.0667.\end{array}$

3. 拥挤程度（sum=19.0005）：
   $\begin{array}{rl}{p}_{A3}& =8.0001/19.0005\approx 0.421,p_{B3}=2.0001/19.0005\approx 0.1053,\\ p_{C3}& =4.0001/19.0005\approx 0.2105,p_{D3}=0.0001/19.0005\approx 0.00000526,\\ p_{E3}& =5.0001/19.0005\approx 0.2632.\end{array}$

4. 票价（sum=50.0005）：
   $\begin{array}{rl}{p}_{A4}& =20.0001/50.0005\approx 0.4,p_{B4}=0.0001/50.0005\approx 0.000002,\\ p_{C4}& =10.0001/50.0005\approx 0.2,p_{D4}=15.0001/50.0005\approx 0.3,\\ p_{E4}& =5.0001/50.0005\approx 0.1.\end{array}$

计算信息熵 $e_j$: $e_j=-\frac{1}{\ln n}\sum _{i=1}^n{p}_{ij}\ln p_{ij},\text{其中}n=5$

1. 风景（$j=1$）：
   $\begin{array}{rl}\sum p_{i1}\ln p_{i1}& \approx 0.1333\ln 0.1333+0.2333\ln 0.2333+0.1667\ln 0.1667+0.2\ln 0.2+0.2667\ln 0.2667\\ & \approx -0.2686-0.3403-0.2989-0.3218-0.3545=-1.5841\\ e_1& =-\frac{1}{\ln 5}(-1.5841)\approx 0.795\end{array}$

2. 人文（$j=2$）：
   $\begin{array}{rl}\sum p_{i2}\ln p_{i2}& \approx 0.1667\ln 0.1667+0.2\ln 0.2+0.2333\ln 0.2333+0.3333\ln 0.3333+0.0667\ln 0.0667\\ & \approx -0.2989-0.3218-0.3403-0.3662-0.1823=-1.5095\\ e_2& =-\frac{1}{\ln 5}(-1.5095)\approx 0.82\end{array}$

3. 拥挤程度（$j=3$）：
   $\begin{array}{rl}\sum p_{i3}\ln p_{i3}& \approx 0.421\ln 0.421+0.1053\ln 0.1053+0.2105\ln 0.2105+0.00000526\ln 0.00000526+0.2632\ln 0.2632\\ & \approx -0.364-0.237-0.330-0.0001-0.351=-1.2821\\ e_3& =-\frac{1}{\ln 5}(-1.2821)\approx 0.796\end{array}$

4. 票价（$j=4$）：
   $\begin{array}{rl}\sum p_{i4}\ln p_{i4}& \approx 0.4\ln 0.4+0.000002\ln 0.000002+0.2\ln 0.2+0.3\ln 0.3+0.1\ln 0.1\\ & \approx -0.3664-0.000026-0.3218-0.3612-0.2303=-1.2797\\ e_4& =-\frac{1}{\ln 5}(-1.2797)\approx 0.795\end{array}$

计算信息效用值 $d_j$ 和权重 $w_j$ $d_j=1-e_j,w_j=\frac{d_j}{\sum _{j=1}^m{d}_j}$

指标	信息熵 $e_j$	信息效用 $d_j=1-e_j$	权重 $w_j=d_j/\sum d_j$
风景	0.795	0.205	$0.205/0.794\approx 25.79\mathrm{\%}$
人文	0.820	0.180	$0.180/0.794\approx 22.68\mathrm{\%}$
拥挤程度	0.796	0.204	$0.204/0.794\approx 25.74\mathrm{\%}$
票价	0.795	0.205	$0.205/0.794\approx 25.79\mathrm{\%}$

# Step 3:计算最优解与最劣解

• 最优解（正理想解）$Z^{+}$：正向指标取归一化最大值1，负向指标取归一化最大值1（因已正向化），即 $Z^{+}=(1,1,1,1)$。
• 最劣解（负理想解）$Z^{-}$：取归一化最小值0，即 $Z^{-}=(0,0,0,0)$。

# Step 4:计算与最优解和最劣解的距离

公式：

$D_i^{+}=\sqrt{\sum _{j=1}^m{w}_j(Z_j^{+}-z_{ij}{)}^2},D_i^{-}=\sqrt{\sum _{j=1}^m{w}_j(Z_j^{-}-z_{ij}{)}^2}$

计算过程（以A为例）：
$\begin{array}{rl}{D}_A^{+}& =\sqrt{0.2579\ast (1-0.000025{)}^2+0.22684\ast (1-0.375{)}^2+0.25737\ast (1-0.9999875{)}^2+0.2579\ast (1-0.999995{)}^2}\\ & \approx \sqrt{0.2579\ast 1+0.22684\ast 0.390625+0+0}\approx \sqrt{0.3464}\approx 0.5886,\\ D_A^{-}& =\sqrt{0.2579\ast (0-0.000025{)}^2+0.22684\ast (0-0.375{)}^2+0.25737\ast (0-0.9999875{)}^2+0.2579\ast (0-0.999995{)}^2}\\ & \approx \sqrt{0+0.22684\ast 0.140625+0.25737\ast 1+0.2579\ast 1}\approx \sqrt{0.5471}\approx 0.7397.\end{array}$

全部结果：

风景地点	$D_i^{+}$	$D_i^{-}$
A	0.58864816	0.73970426
B	0.68956081	0.46675749
C	0.55297597	0.48326338
D	0.58134203	0.66059147
E	0.63882607	0.61200454

# Step 5:计算综合得分与排序

公式：

$C_i=\frac{D_i^{-}}{D_i^{+}+D_i^{-}},C_i\text{越大，评价对象越优}$

计算结果：

风景地点	综合得分$C_i$	排序
A	$\frac{0.7397}{0.5886+0.7397}\approx 0.5569$	1
B	$\frac{0.4668}{0.6896+0.4668}\approx 0.4037$	5
C	$\frac{0.4833}{0.5530+0.4833}\approx 0.4664$	4
D	$\frac{0.6606}{0.5813+0.6606}\approx 0.5319$	2
E	$\frac{0.6120}{0.6388+0.6120}\approx 0.4893$	3

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] Shih H S, Shyur H J, Lee E S. An extension of TOPSIS for group decision making[J]. Mathematical & Computer Modelling, 2007, 45(7):801-813.
[3] 刘浩然,汤少梁. 基于 TOPSIS 法与秩和比法的江苏省基本医疗服务均等化水平研究[J]. 中国全科医学,2016,19(7):819-823. DOI:10.3969/j.issn.1007-9572.2016.07.017.