耦合协调度

操作视频

SPSSPRO教程-耦合协调度

# 主成分分析（PCA）

# 1、作用

耦合协调度模型用于分析事物的协调发展水平。耦合度指两个或两个以上系统之间的相互作用影响，实现协调发展的动态关联关系，可以反映系统之间的相互依赖相互制约程度。协调度指耦合相互作用关系中良性耦合程度的大小，它可体现出协调状况的好坏。

# 2、输入输出描述

输入:至少两项或以上的定量变量.
输出:以样本（行）为单位，各个单位综合各个变量的耦合协调程度

# 3、案例示例

案例：以 2018 年东部地区科技金融与技术创新的耦合协调关系进行分析。

# 4、案例数据

耦合协调度分析案例数据

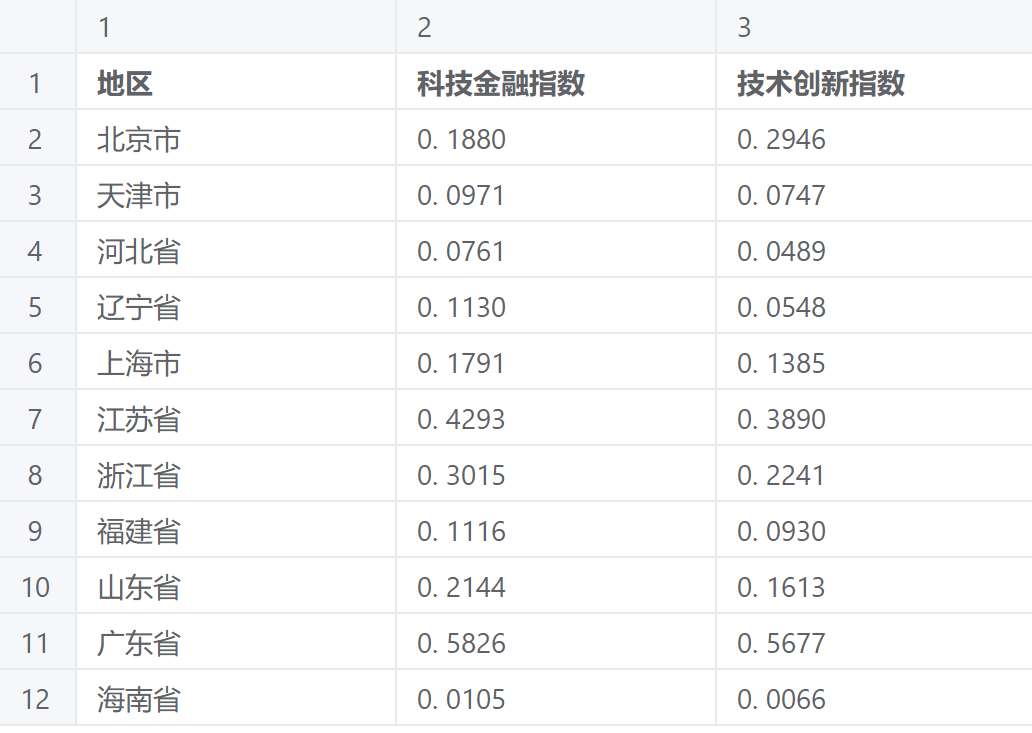
# 5、案例操作

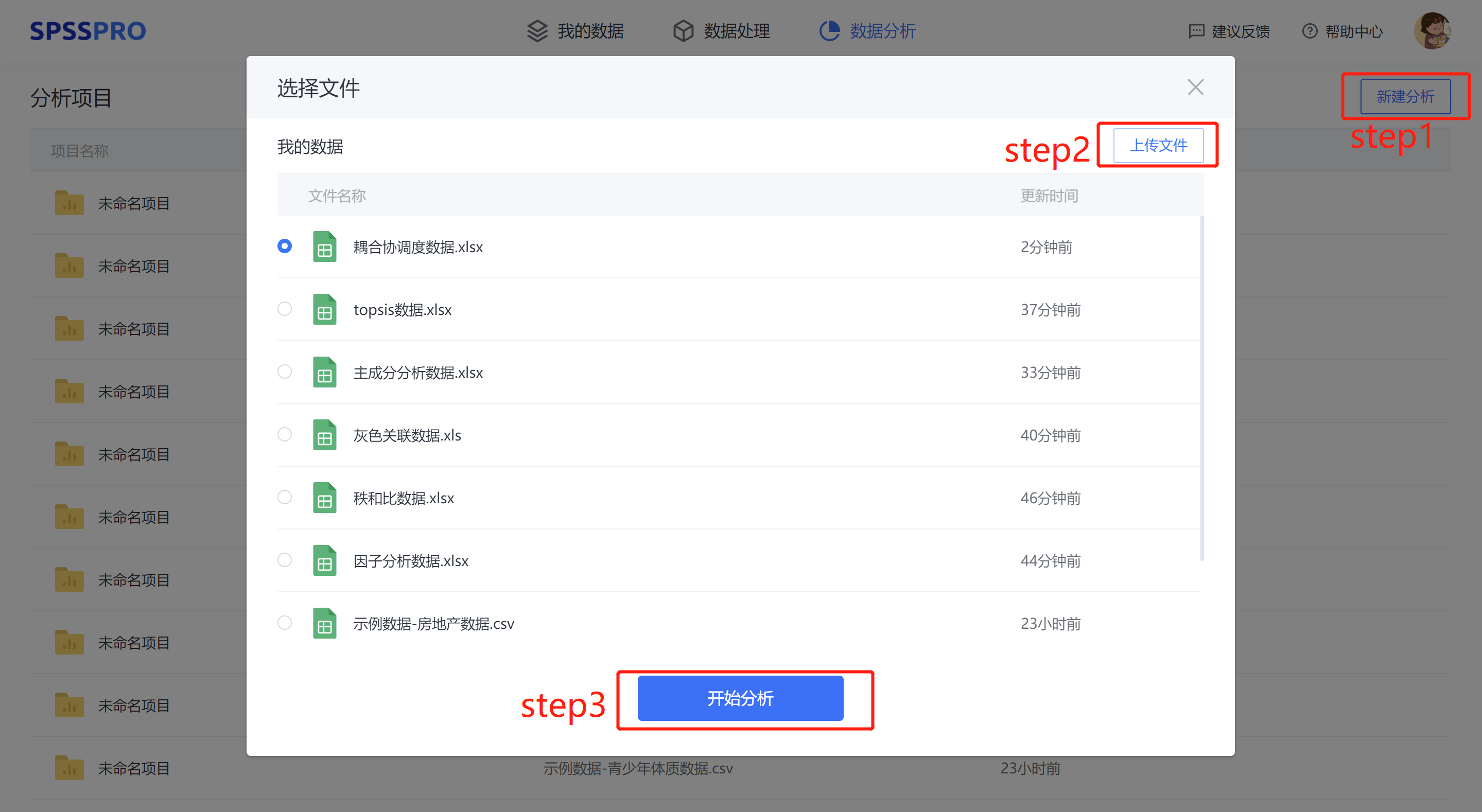
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；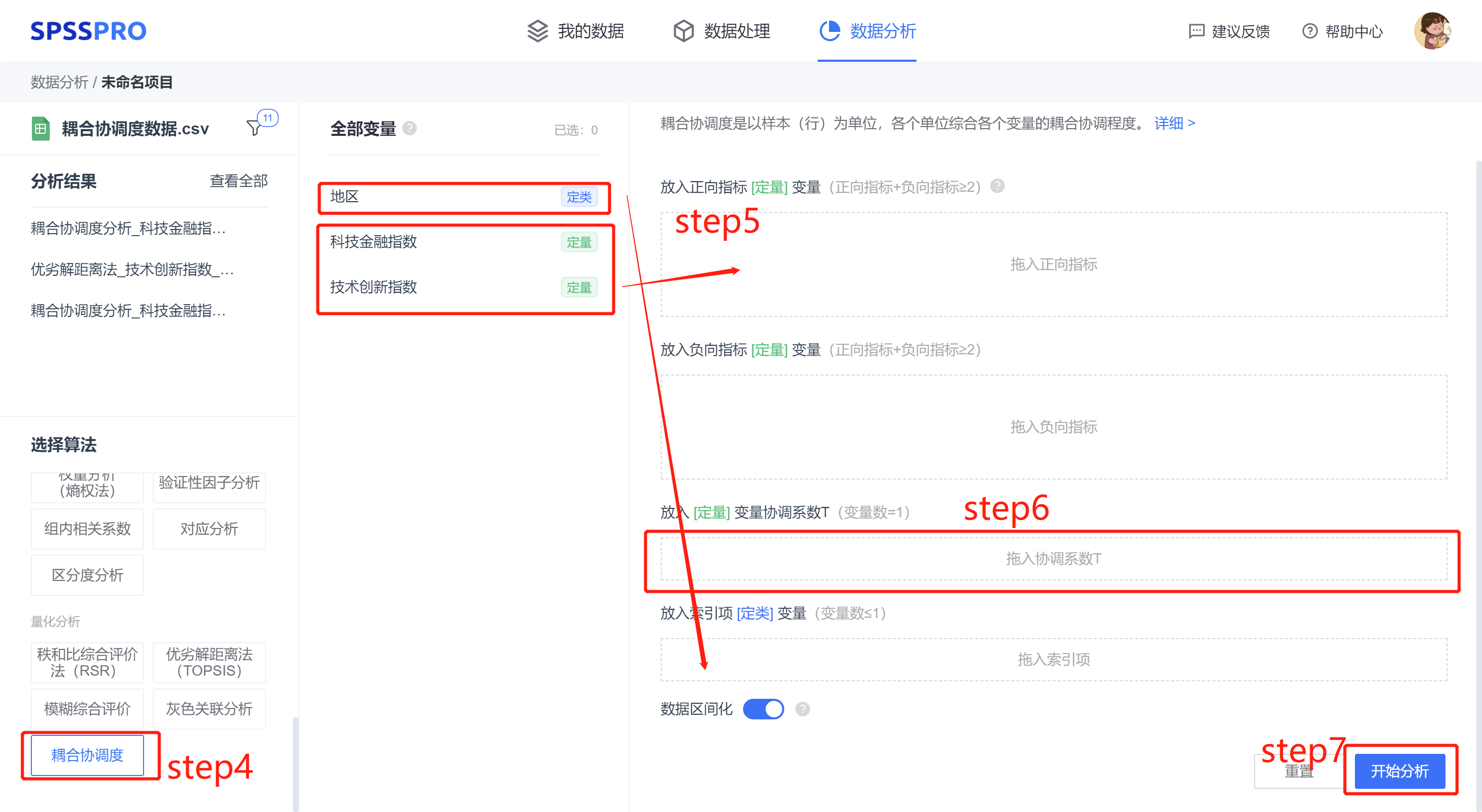

step4：选择【耦合协调度】；
step5：查看对应的数据数据格式，【耦合协调度】要求特征序列为定量变量，分为正向指标变量和负向指标变量，且正向指标变量和负向指标变量的个数之和大于等于两项。
step6：（放入变量协调系数 T：如果自己有协调系数数据，那么可放置在页面对应框中，此时，SPSSPRO 不会自动计算协调指数，而是直接使用用户提供的协调系数数据。）
step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

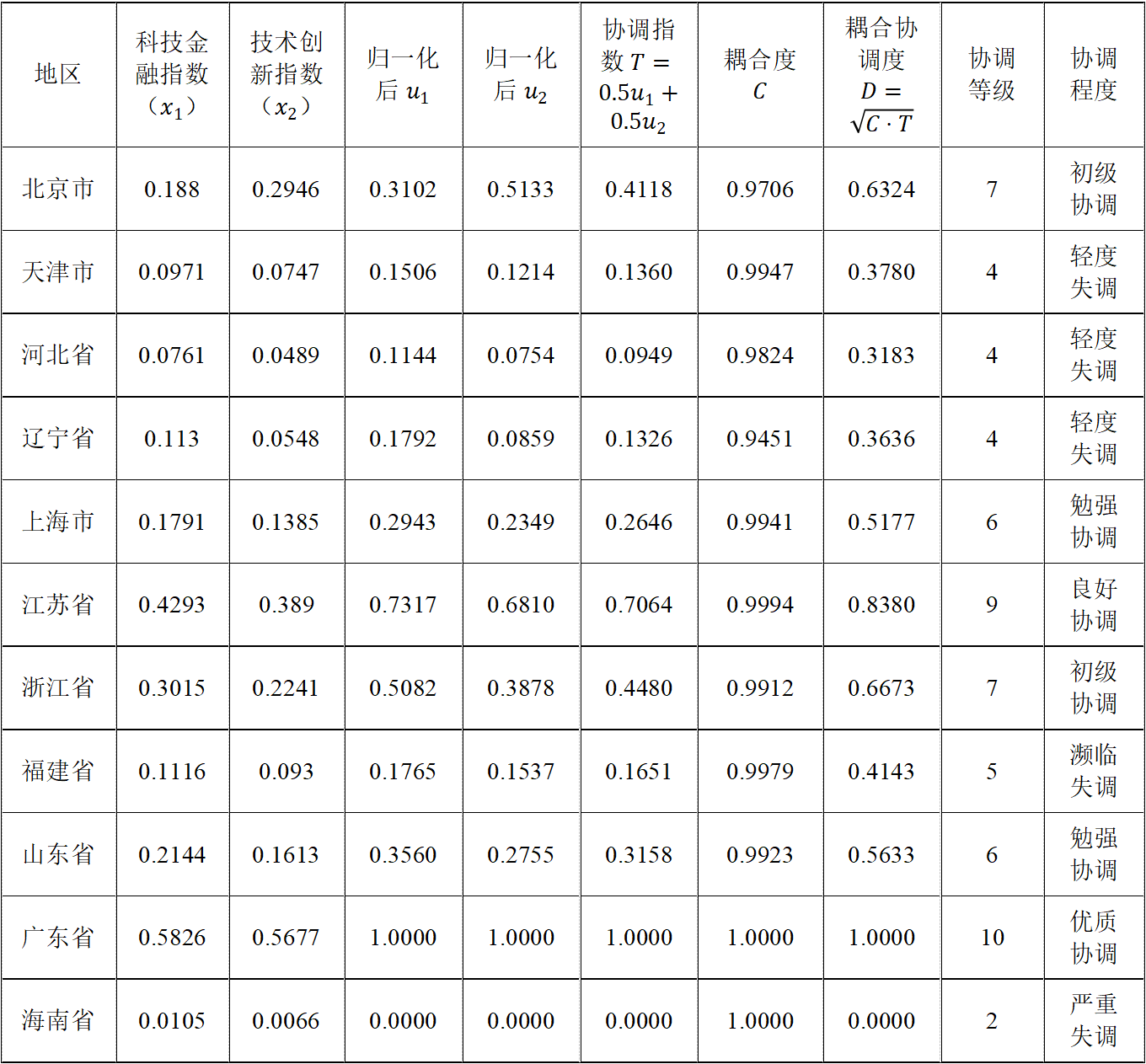
输出结果 1：耦合协调度计算结果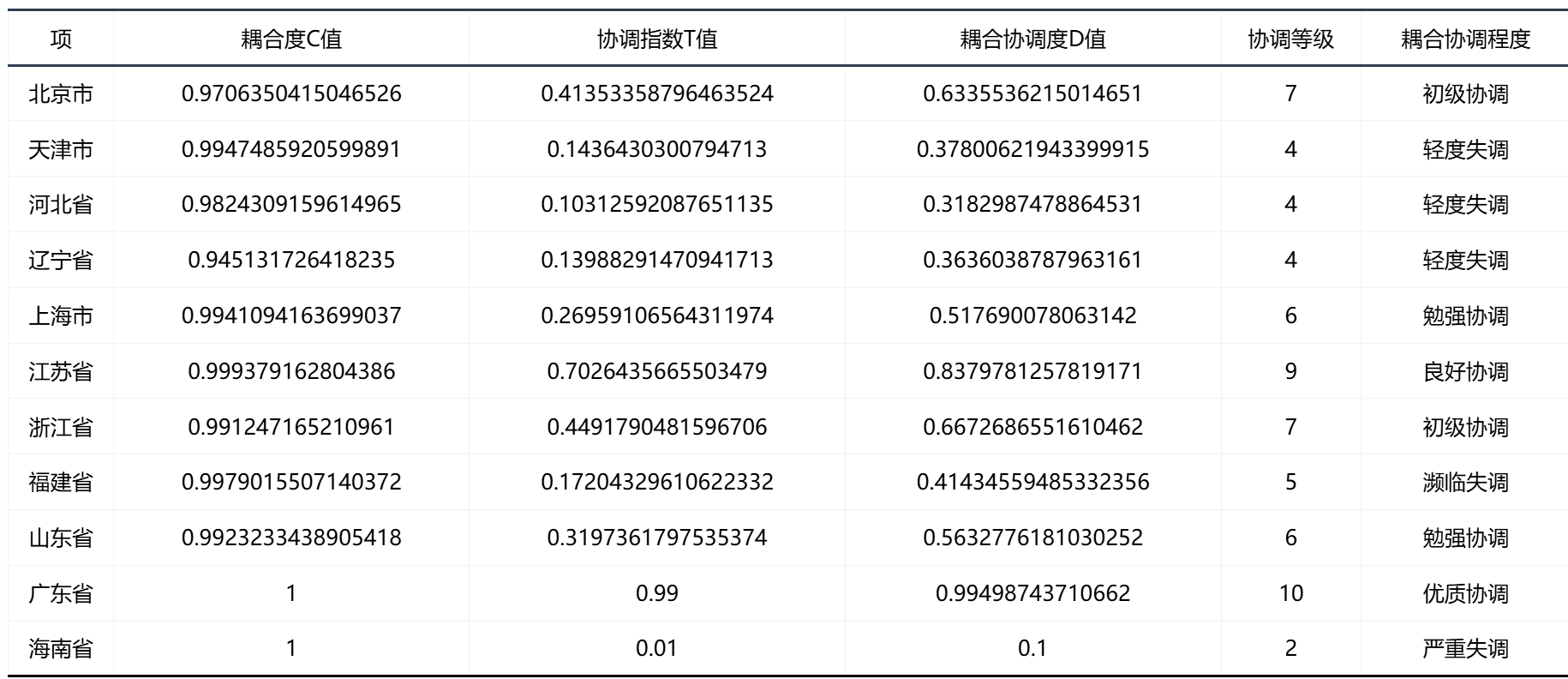 

分析:由表可知，海南省的科技金融和技术创新的耦合度协调等级最低，达到严重失调的程度，而广东省的科技金融和技术创新的耦合度协调等级最高，达到优质协调的程度。

输出结果 2：耦合协调度等级划分标准

协调等级	协调程度
1	极度失调
2	严重失调
3	中度失调
4	轻度失调
5	濒临失调
6	勉强协调
7	初级协调
8	中级协调
9	良好协调
10	优质协调

图表说明：耦合协调度等级划分标准如上表所示。

# 7、注意事项

输入变量必须进行数据归一化处理，且介于 0~1 之间，这样最终计算得到的 D 值才会介于 0~1 之间，并且得到正确的耦合协调度等级判断；
耦合协调度研究系统与系统之间的耦合协调情况。系统通常会由多个指标表示，此时需要将多个指标"合并"成一个。一般情况下可使用两种方法，分别是主成分分析或熵值法进行处理。

# 8、模型理论

耦合最早是作为一个物理学的概念，指 2 个或 2 个以上系统或运动形式通过各种相互作用而彼此影响的现象，多个系统相互作用耦合度模型可以用一下模型表示

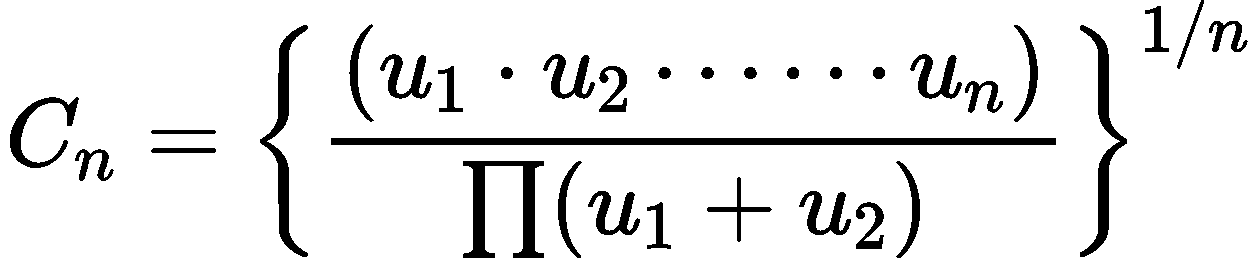
式中 Cn 为 n 元系统的耦合度；u1…un 分别为第一个子系统到第 n 个子系统对总系统有序度的贡献，计算方法如下

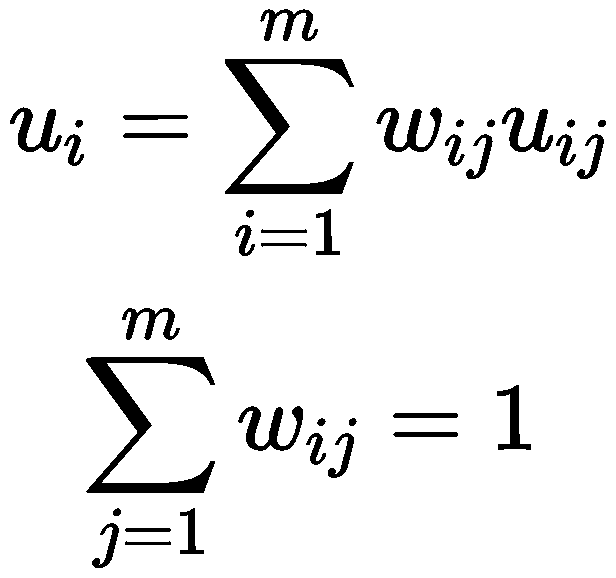
式中 ui 为第 i 个子系统对总系统有序度的贡献；uij 为第 i 个子系统中第 j 个指标的归一化值；wij 为第 i 个子系统中第 j 个指标的权重，每个子系统中指标的权重计算使用熵权法进行计算。
在计算每个子系统的熵权时，必须先进行归一化处理，这里采用最大最小值法进行归一化处理：当 uij 为数值越大对系统越好时（正向归一化）

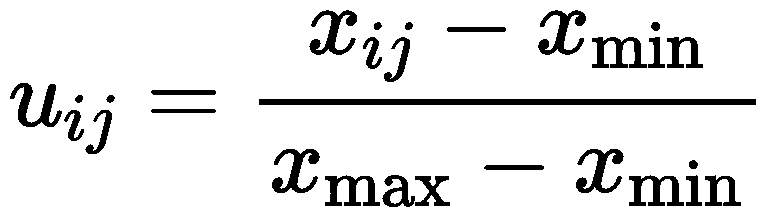
uij 为数值越小对系统越好时（负向归一化）

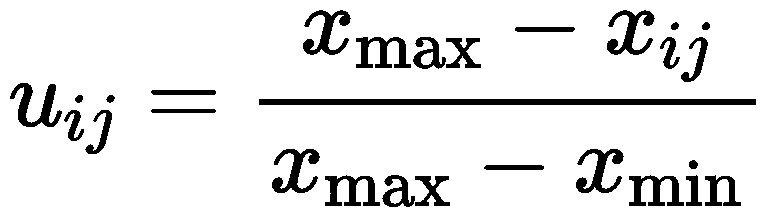
由于耦合度指标在有些情况下却很难反映出子系统整体“功效”与“协同”效应，耦合度各子系统指标的上下限取自各指标的极值，而极值存在动态、不平衡的特性，单纯依靠耦合度判别有可能产生误导，由此，提出了耦合协调度。以科技金融与技术创新的二元耦合协调模型为例,

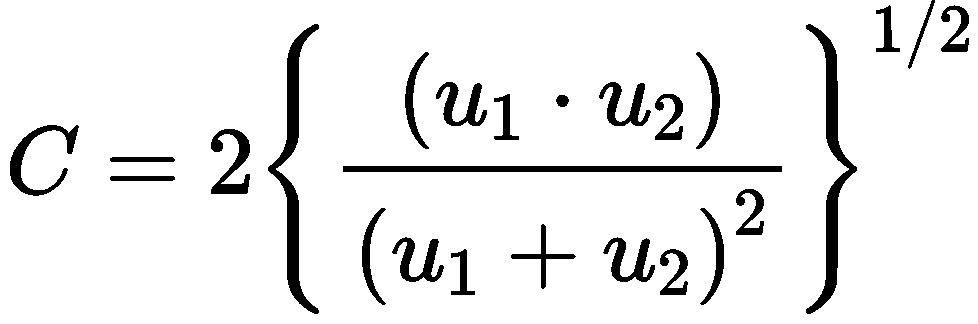
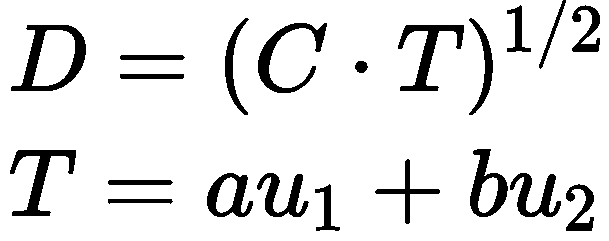
其中 C 为耦合度，D 为耦合协调度，u1 和 u2 分别表示科技金融指数与技术创新指数，a 和 b 分别指科技金融指数与技术创新指数的权重。

# 9、手推步骤

Step 1：数据归一化处理
采用最大-最小值法对科技金融指数（ $x_{1}$ ）和技术创新指数（ $x_{2}$ ）进行正向归一化：

$u_{1} = \frac{x_{1} - x_{1, min}}{x_{1, max} - x_{1, min}}, u_{2} = \frac{x_{2} - x_{2, min}}{x_{2, max} - x_{2, min}}$

其中：

$x_{1, max} = 0.5826$ （广东省）， $x_{1, min} = 0.0105$ （海南省）

$x_{2, max} = 0.5677$ （广东省）， $x_{2, min} = 0.0066$ （海南省）

示例计算（北京市）：

$u_{1} = \frac{0.188 - 0.0105}{0.5826 - 0.0105} = \frac{0.1775}{0.5721} \approx 0.3102$

$u_{2} = \frac{0.2946 - 0.0066}{0.5677 - 0.0066} = \frac{0.288}{0.5611} \approx 0.5133$

Step 2: 计算协调指数 $T$
假设权重 $a = b = 0.5$ （等权重）：

$T = 0.5 u_{1} + 0.5 u_{2}$

北京市：

$T = 0.5 \times 0.3102 + 0.5 \times 0.5133 = 0.4118$

Step 3: 计算耦合度 $C$
公式：

$C = 2 \sqrt{\frac{u_{1} \cdot u_{2}}{(u_{1} + u_{2})^{2}}}$

北京市：

$C = 2 \sqrt{\frac{0.3102 \times 0.5133}{(0.3102 + 0.5133)^{2}}} = 2 \sqrt{\frac{0.1593}{{0.8235}^{2}}} \approx 2 \times 0.4853 \approx 0.9706$

Step 4：计算耦合协调度
公式：

$D = \sqrt{C \cdot T}$

北京市：

$D = \sqrt{0.9706 \times 0.4118} \approx \sqrt{0.3999} \approx 0.6324$

Step 5: 整合等级排序、划分耦合度等级

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 陈伟忠,周春应. 中国区域科技金融与技术创新耦合协调度分析[J]. 生产力研究,2021(6):113-118.
[3] 贾路,任宗萍,李占斌,等. 基于耦合协调度的大理河流域径流和输沙关系分析[J]. 农业工程学报,2020,36(11):86-94.

建议反馈