二分类概率单位回归(Probit)
# 1、作用
二分类概率单位回归（Probit Regression）是一种广义的线性模型，用于处理因变量Y为二分类（binary）变量的回归分析。在这种情况下，Y只能取两个值（例如，0和1，代表“成功”与“失败”、“是”与“否”等）。Probit模型通过假设一个潜在的连续变量（通常称为潜变量）与自变量X之间存在线性关系，并通过这个潜变量与阈值（通常是0）的比较来决定Y的取值。具体来说，当潜变量大于0时，Y取值为1；当潜变量小于或等于0时，Y取值为0。
由于Probit模型使用正态分布的累积分布函数（CDF）来连接潜变量和观察到的二分类因变量，因此它能够捕捉到因变量与自变量之间的非线性关系，并且允许误差项服从正态分布。
# 2、输入输出描述
输入 ：自变量 X 为1个或1个以上的定类或定量变量，因变量 Y 为一个定类变量。
输出 ：模型输出的分析结果及模型的预测效果。
# 3、案例示例
案例：根据员工满意度、月均工作小时、工伤事故、薪资水平四个影响因素(自变量)研究员工是否离职。
# 4、案例数据
# 5、案例操作
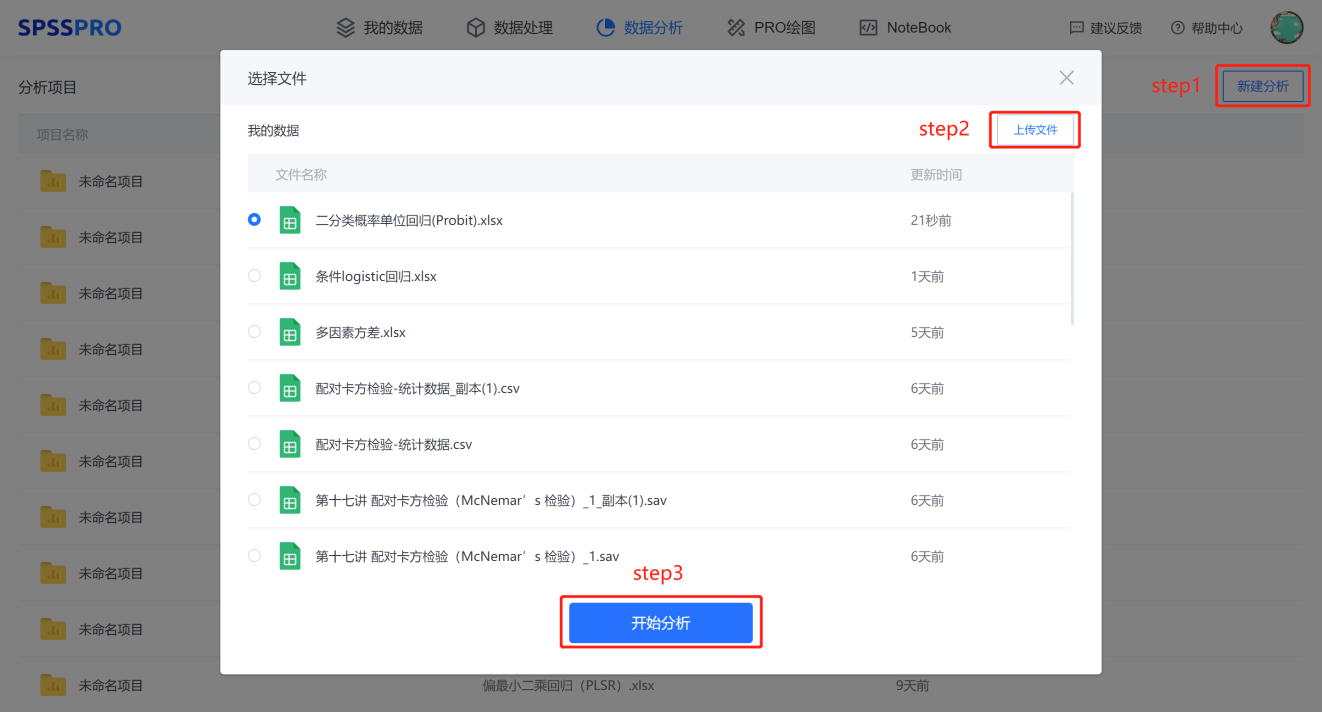
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；
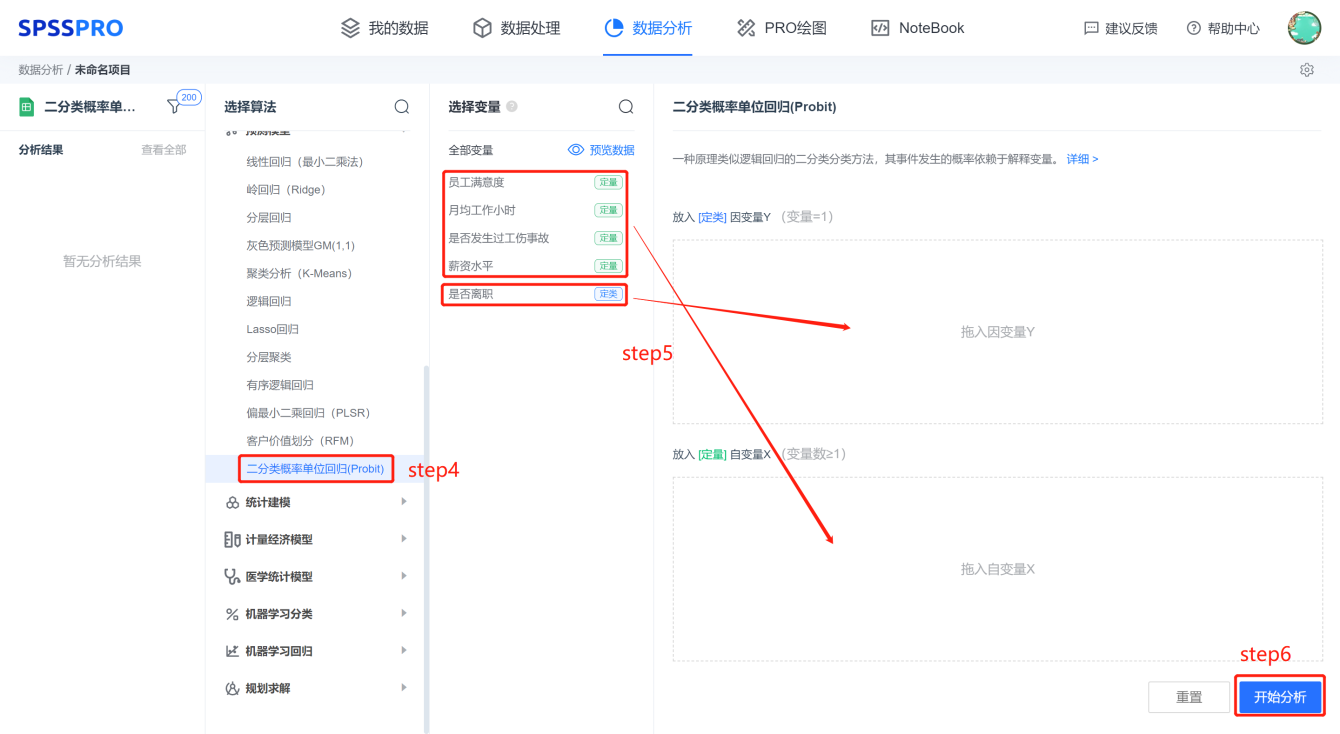
step4：选择【二分类概率单位回归】；
step5：查看对应的数据数据格式，按要求输入【二分类概率单位回归】数据;
step6：点击【开始分析】，完成全部操作。
# 6、输出结果分析
输出结果 1：二分类因变量基本汇总
| 因变量 | 选项 | 频数 | 百分比 |
|---|---|---|---|
| 是否离职 | 1.0 | 39 | 19.50% |
| 0.0 | 161 | 80.50% | |
| 总计 | 200 | 100.00% |
图表说明：
上表展示了因变量各分组的分布情况。
● 选项：当前字段数据下的去重类别。
● 频数：当前去重类别在数据中出现的次数。
● 百分比：当前变量的频数占比。
● 当因变量分类水平的数据量出现严重不平衡时，建议对数据进行过采样或者欠采样。
输出结果2：模型评价
| 似然比卡方 | p值 | AIC值 | BIC值 |
|---|---|---|---|
| 157.361 | 0.000*** | 167.361 | 183.853 |
图表说明：
上表展示了模型评价指标，可用于对模型的表现进行评估或有效性进行验证，其包括似然比检验，p值，AIC值、BIC值。
● 对p值进行分析，如果该值小于0.05，则说明模型有效；反之则说明模型无效。
● AIC 值和BIC 值用于对比两个模型的优劣时使用，此两个值均为越小越好。
分析：模型的似然比卡方检验的结果显示，显著性𝑝值0.000***，水平上呈现显著性，拒绝原假设，因而模型是有效的。
输出结果3：二分类概率单位回归结果
| 项 | 回归系数 | 标准误差 | z值 | p值 | 边际效应 | 95%置信区间 | |
|---|---|---|---|---|---|---|---|
| 上限 | 下限 | ||||||
| 常数 | -0.208 | 0.606 | -0.343 | 0.731 | -1.397 | 0.98 | |
| 员工满意度 | 2.852 | 0.5 | 5.699 | 0.000*** | 0.626 | 1.871 | 3.832 |
| 月均工作小时 | -0.001 | 0.002 | -0.707 | 0.479 | 0 | -0.006 | 0.003 |
| 是否发生过工伤事故 | -0.121 | 0.314 | -0.385 | 0.700 | -0.027 | -0.736 | 0.495 |
| 薪资水平 | -0.115 | 0.182 | -0.633 | 0.527 | -0.025 | -0.473 | 0.242 |
| 注：*、、*分别代表1%、5%、10%的显著性水平 |
图表说明：
上表展示了模型的参数结果。包括模型的系数、标准误差、边际效应值、置信区间等用于分析模型的公式。
● 对于连续自变量的边际效应值的意义为：该自变量每增加一个单位，带来因变量的概率上升或下降多少百分比。
● 对于哑变量化的0-1分类自变量的边际效应值意义为：该变量每升高一个单位（即分类水平从0变为1），发生因变量的概率上升或下降了多少百分比。
智能分析：
字段员工满意度显著性𝑝值为0.000***，水平上呈现显著性，拒绝原假设，因此员工满意度会对是否离职产生显著性影响，意味着员工满意度每增加一个单位，是否离职为1.0的概率比0.0的几率增加或减少了62.581%。
字段月均工作小时显著性𝑝值为0.479，水平上不呈现显著性，不能拒绝原假设，因此月均工作小时不会对是否离职产生显著性影响。 字段是否发生过工伤事故显著性𝑝值为0.700，水平上不呈现显著性，不能拒绝原假设，因此是否发生过工伤事故不会对是否离职产生显著性影响。
字段薪资水平显著性𝑝值为0.527，水平上不呈现显著性，不能拒绝原假设，因此薪资水平不会对是否离职产生显著性影响。
输出结果4：混淆矩阵热力图
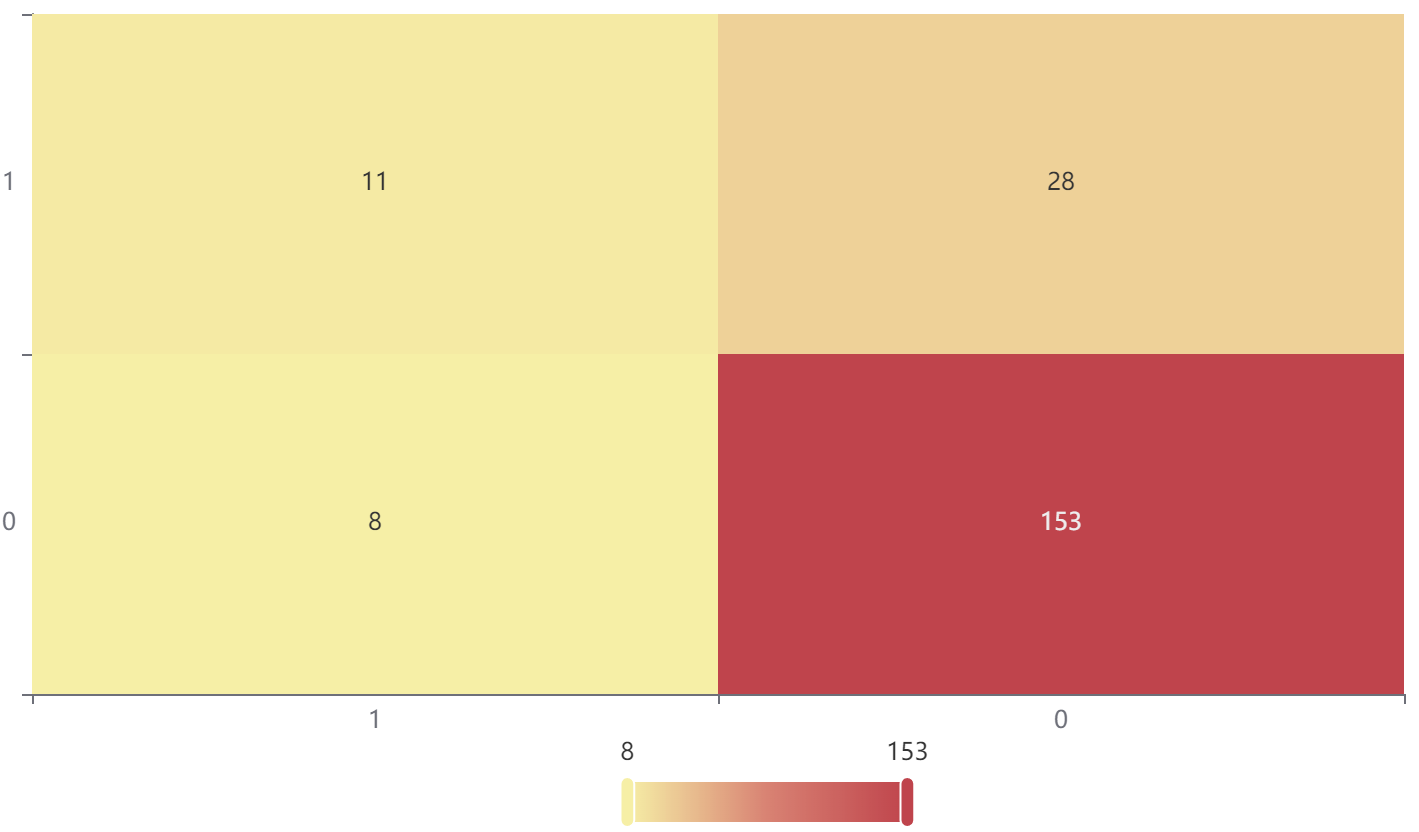
图表说明：上图以热力图的形式展示了混淆矩阵。
输出结果5：ROC曲线
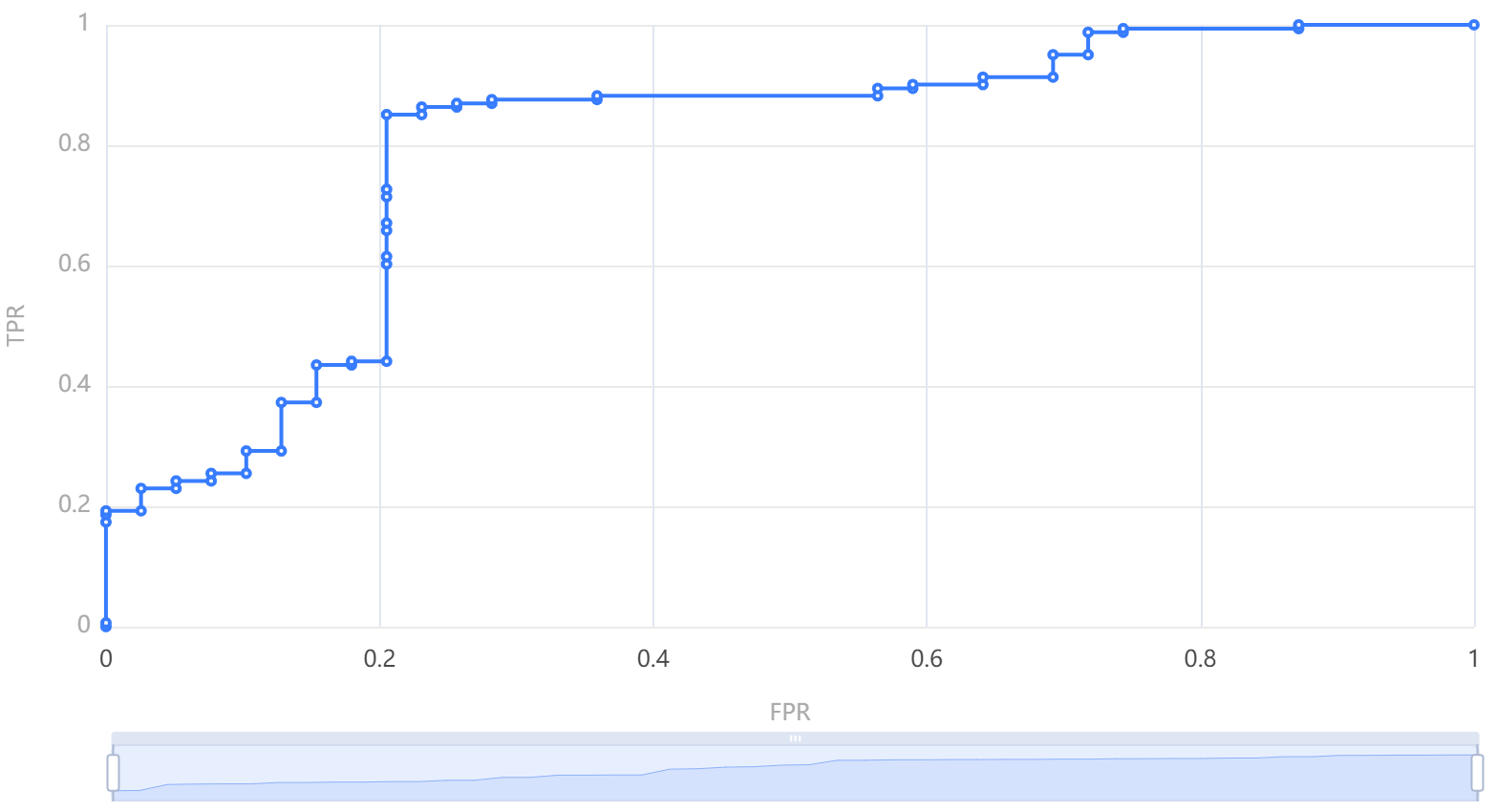
图表说明：
上图展示了ROC曲线图，用于衡量二分类概率单位回归的分类效果。
● ROC曲线图把灵敏度（TPR）和特异度（FPR）结合，可以同时衡量两者关系。理想情况下，TPR应该接近1，FPR应该接近0。
● 灵敏度：实际为正样本的结果中，预测为正样本的比例。
● 特异度：实际为负样本的结果中，预测为正样本的比例。
输出结果6：分类评价指标
| 准确率 | 召回率 | 精确率 | F1 | AUC |
|---|---|---|---|---|
| 0.82 | 0.82 | 0.793 | 0.794 | 0.799 |
图表说明：
上表中展示了分类评价指标，进一步通过量化指标来衡量二分类概率单位回归的分类效果。
准确率：预测正确样本占总样本的比例，准确率越大越好。
召回率：实际为正样本的结果中，预测为正样本的比例，召回率越大越好。
精确率：预测出来为正样本的结果中，实际为正样本的比例，精确率越大越好。
F1：精确率和召回率的调和平均，精确率和召回率是互相影响的，虽然两者都高是一种期望的理想情况，然而实际中常常是精确率高、召回率就低，或者召回率低、但精确率高。若需要兼顾两者，那么就可以用F1指标。
AUC：AUC值越接近1说明分类效果越好。
# 7、注意事项：
- 在使用Probit模型之前，需要对自变量进行适当的预处理，如处理缺失值、转换分类变量为虚拟变量等
- 因变量 Y 是二分类变量
- 有至少1个自变量，自变量可以是连续变量，也可以是分类变量
- 每条观测间相互独立。分类变量（包括因变量和自变量）的分类必须全面且每一个分类间互斥
- 自变量之间无多重共线性
- 自变量中分类变量较多时，可考虑使用Logistic回归
- 当自变量中连续变量较多且符合正态分布时，使用Probit回归
# 8、模型理论
# 1.背景介绍
一般情况下，在我们研究的回归模型中，都隐含的假定了因变量（Y）是定量的，而解释变量（X）是定量、定性（或虚拟变量）。
当因变量（Y）为二值定性的情况：比如一个家庭是否拥有一所住房，如拥有 Y=1，不拥有 Y=0，则被称为线性概率模型。
当因变量为二值时，X 与 Y 的关系如图中的点:
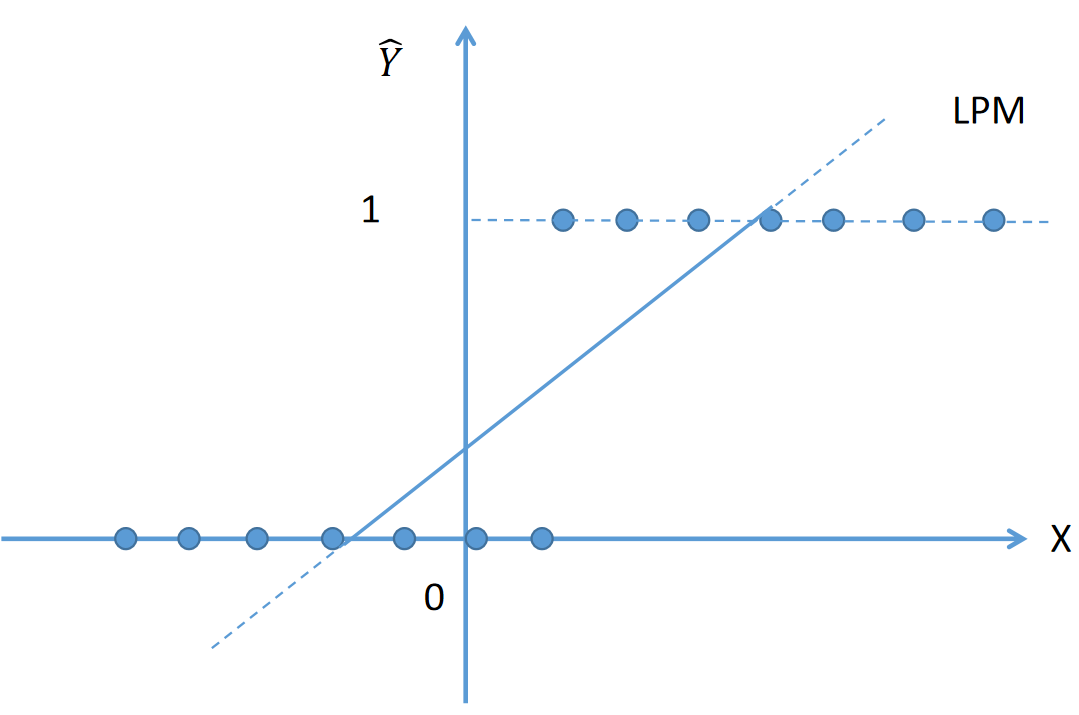
要预测的值
为期望
，令 
。 # 2.线性概率模型
若用线性概率模型拟合因变量时，则会存在以下问题：
- 由于 E(Yi / Xi) 度量给定 X 事件下 Y 发生的概率，因此概率必须落在0与1之间，LPM无法保证的估计值落在 0 与 1 之间；
- 对于给定的 X，Y = 0 或Y= 1，因此所有的 Y 值必须落在 X 轴或者 Y=1 的一条直线上。而线性模型则无法很好的模拟这样的散点。
- 线性回归模型假定 Y 估计值随 X 而线性增加，即 X 的边际或临界效应（X连续增加的每一单位中所得到的Y增量）一直保持不变（一般边际效用是递减的）。
# 3.Logit模型
标准累计 Logistic 分布的函数：
建立 logit 与线性回归的关系：
，可变换为
，可解决上述线性概率模型的问题，可以很好的进行拟合。
# 4.Probit模型
当回归中因变量取 0 或 1 时，很容易使用 CDF（累计分布函数）取建立回归模型。当选用 logistic 时，称为logit模型，详细可见SPSSPRO逻辑回归帮助文档；选用正态分布函数时，则是profit模型。
Logit模型是Logistic函数的累积概率函数，同样的，正态函数记为
，Probit 变换与 Probit 回归模型如下：
，对应的累计概率函数，即标准正态分布的累积概率函数：
，如下图
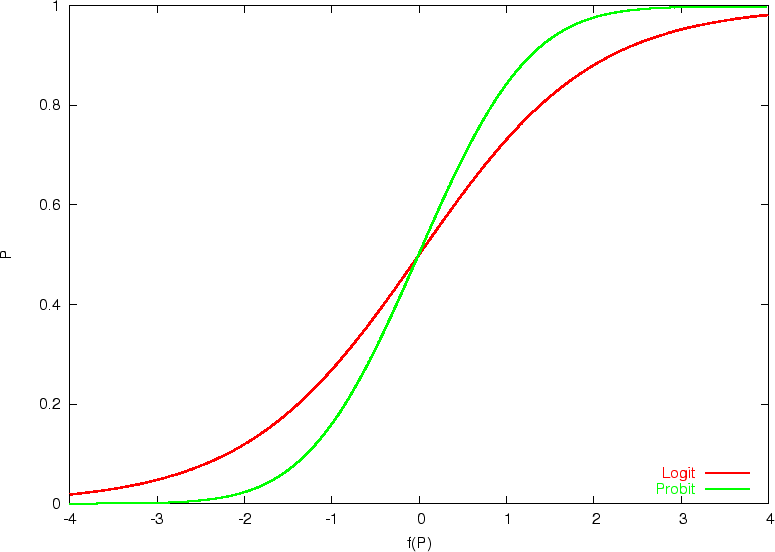
绿色曲线为Probit，红色曲线为Logit，可见Probit模型与Logit模型很相似，可用于解决上面的二分类问题。
# 5.极大似然法估计参数
个体（非群组）数据的 Probit 模型的极大似然估计，假设我们对给定个人收入 X 的情况下估计一个人拥有住房的概率感兴趣，我们还假定这个概率可由 Probit 函数表示：
我们不能实际观测 
，只能观测到结果 Y=1(有房)和 Y=0（无房）。
每个都是一个伯努利随机变量，所以可写成：
假设我们有一个 n 次观测的随机样本。令
表示
或 0 的概率，观测到 n 个 Y 值的联合概率，即
为： 
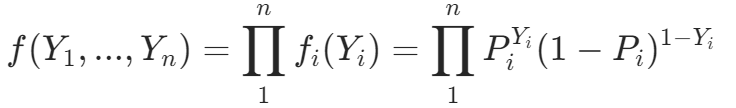（1）每个 Yi 都是独立的，而且有相同的 logistic 密度函数，所以可以将联合密度函数写成个别密度函数的乘积。
我们对（1）取对数，便得到对数似然函数LLF:
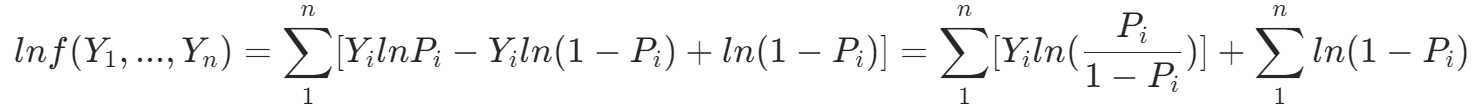
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 周志华，机器学习，清华大学出版社，2016.