偏最小二乘回归(PLSR)
# 1、作用
偏最小二乘回归 (PLSR) 是一种多因变量对多自变量的回归建模方法,是最小二乘方法的推广。用于解决两组多重相关变量间的相互依赖关系,并研究用一组变量(自变量或预测变量)去预测另一组变量(因变量或响应变量)。
# 2、输入输出描述
输入:一组预测变量和一组响应变量。
输出:偏最小二乘回归结果,包括自变量累计投影重要性、成分矩阵表和模型系数结果等。
# 3、案例示例
案例:某康复俱乐部对20名中年人测量了三个生理指标:体重 x1, 腰围 x2, 脉搏 x3;三个训练指标:单杠 y1, 弯曲 y2, 跳高 y3。用偏最小二乘回归建立由三个生理指标分别预测三个训练指标的回归模型。
# 4、案例数据
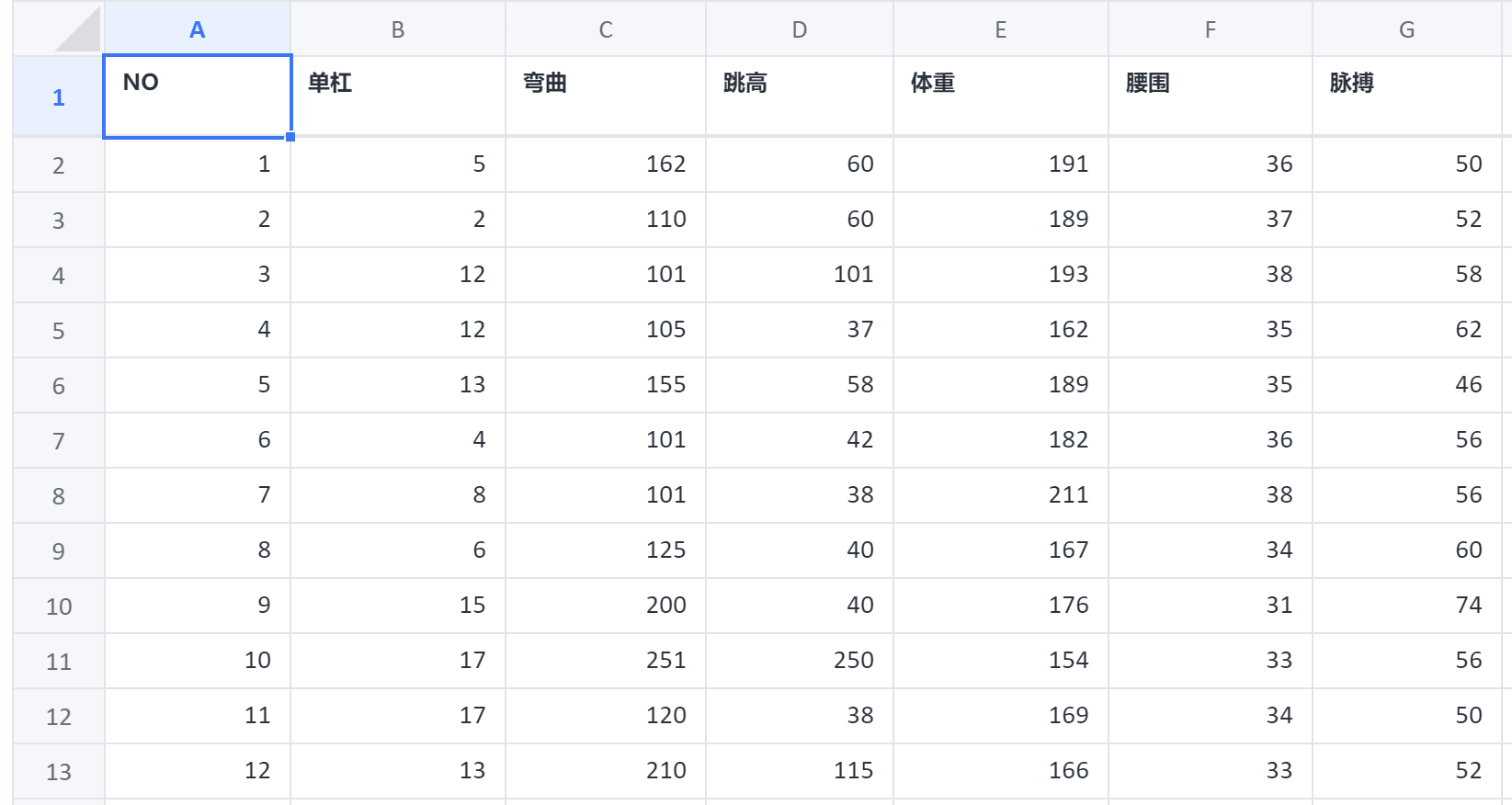
# 5、案例操作
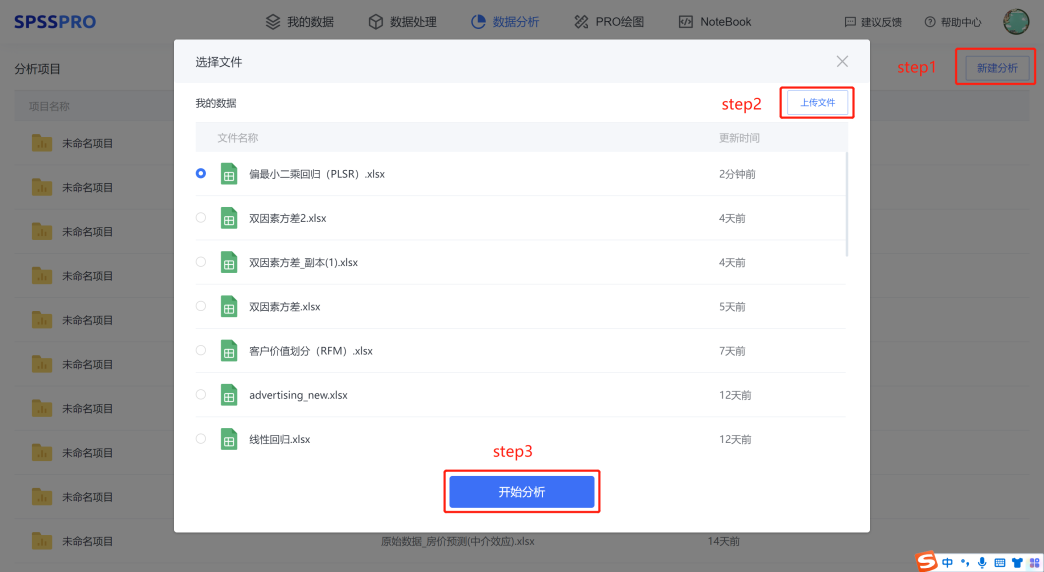
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;
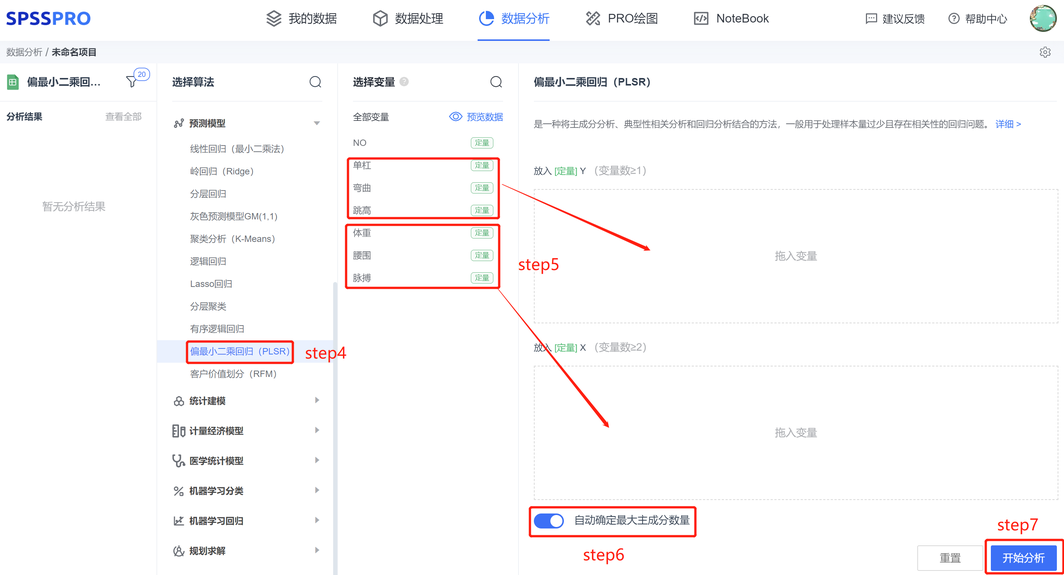
step5:查看对应的数据数据格式,按【偏最小二乘回归(PLSR)】要求输入多个定量变量X和多个定量变量Y;
step6:选择是否自动确定最大主成分数量;
step7:点击【开始分析】,完成全部操作。
# 6、输出结果分析
输出结果1:因子方差解释情况表
| 潜在因子 | X方差 | 累计的X方差 | Y方差 | 累计的Y方差(R方) | 调整后的R方 |
|---|---|---|---|---|---|
| 1 | 0.701 | 0.701 | 0.209 | 0.209 | 0.166 |
| 2 | 0.255 | 0.957 | 0.029 | 0.239 | 0.149 |
| 3 | 0.043 | 1 | 0.038 | 0.277 | 0.141 |
图表说明:上表展示潜在因子的信息综合解释能力。其中,累计的X方差代表对自变量信息的提取,累计的Y方差(R方)代表对因变量信息的提取,可以以此为依据确定参数最大主成分数量。
分析:因子对方差解释情况表的结果显示,前【2】个潜在因子就可解释自变量80%的信息,全部潜在因子也不能解释因变量80%的信息。
输出结果2:自变量VIP(累积投影重要性)汇总表
| 变量 | 因子1 | 因子2 | 因子3 |
|---|---|---|---|
| 体重 | 1.022 | 0.998 | 1.019 |
| 腰围 | 1.336 | 1.298 | 1.22 |
| 脉搏 | 0.414 | 0.565 | 0.689 |
图表说明:上表展示VIP(累积投影重要性)的情况,它表示成分个数不同时,X对于Y的解释重要性力度,也可以用于参考最大主成分数量。其中对于VIP很大(大于1)的自变量,它在解释潜在因子(从而在解释因变量)时作用相对更大一些。
输出结果3:自变量VIP(累积投影重要性)图
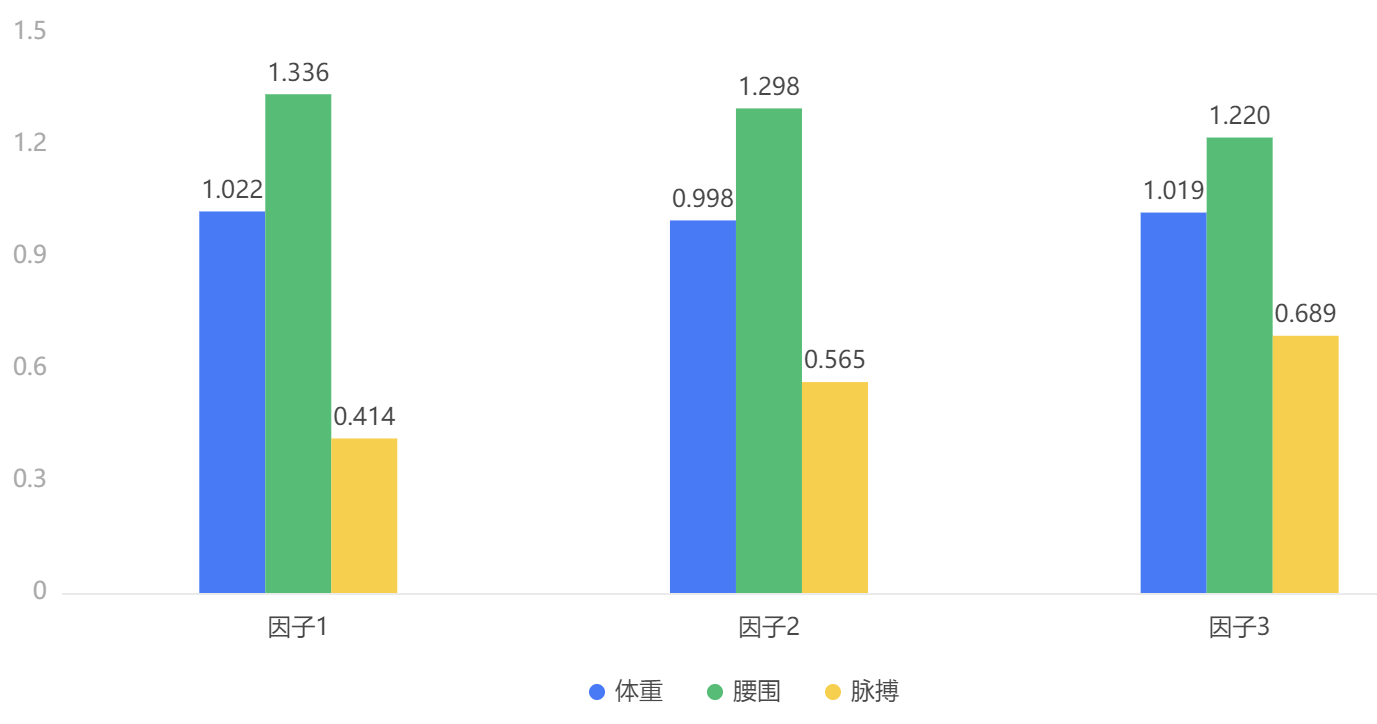
图表说明:上图将VIP(累积投影重要性)的情况可视化的展示出来。
输出结果4:成分矩阵表
| 变量 | 因子1 | 因子2 | 因子3 |
|---|---|---|---|
| 体重 | 0.59 | -0.368 | 0.935 |
| 腰围 | 0.771 | 0.7 | -0.802 |
| 脉搏 | -0.239 | 0.636 | 0.223 |
| 单杠 | 6.778 | -11.376 | -1.071 |
| 弯曲 | -7.602 | 10.434 | 1.913 |
| 跳高 | -1.068 | -3.185 | -3.01 |
图表说明:由上表可得到主成分分析降维后的成分矩阵表。
输出结果5:因子载荷系数表
| 变量 | 因子1 | 因子2 | 因子3 |
|---|---|---|---|
| 体重 | 0.666 | 0.02 | 0.657 |
| 腰围 | 0.676 | 0.355 | -0.287 |
| 脉搏 | -0.359 | 1.194 | 0.697 |
| 单杠 | -0.342 | -0.336 | 0.477 |
| 弯曲 | -0.416 | -0.291 | 0.455 |
| 跳高 | -0.143 | -0.065 | -0.213 |
图表说明:上表为因子载荷系数表,可以分析到每个因子中隐变量的重要性。
输出结果6:模型系数结果表
| 单杠 | 弯曲 | 跳高 | 单杠(标准化) | 弯曲(标准化) | 跳高(标准化) | |
|---|---|---|---|---|---|---|
| 常数 | 47.968 | 623.282 | 179.887 | 0 | 0 | 0 |
| 体重 | 0.079 | 0.728 | -0.538 | 0.368 | 0.287 | -0.259 |
| 腰围 | -1.456 | -17.387 | 0.234 | -0.882 | -0.89 | 0.015 |
| 脉搏 | -0.019 | 0.139 | -0.389 | -0.026 | 0.016 | -0.055 |
图表说明:展示了本次PLS模型结果,主要包括模型的系数,用于分析自变量X对于因变量Y的影响关系情况。
分析:模型的标准化公式为: 单杠 = 47.968+0.079 * 体重-1.456 * 腰围-0.019 * 脉搏 弯曲 = 623.282+0.728 * 体重-17.387 * 腰围+0.139 * 脉搏 跳高 = 179.887-0.538 * 体重+0.234 * 腰围-0.389 * 脉搏
# 7、注意事项
- 预测变量可以是连续的定量变量或定类变量
- 响应变量应当是连续变量
- 预测变量无需固定
# 8、模型理论
# 1.简介
偏最小二乘回归 (PLSR) 是一种多因变量对多自变量的回归建模方法,是最小二乘方法的推广。用于解决两组多重相关变量间的相互依赖关系,并研究用一组变量(自变量或预测变量)去预测另一组变量(因变量或响应变量)。
当两组变量的个数很多,且线性相关,而观测数据的数量又较少时,适合用偏最小二乘回归建立的模型。
偏最小二乘回归有如下优点:
- 提供了一种多因变量对多自变量的回归建模方法;
- 有效地解决变量之间的多重共线性问题;
- 适合当样本点数量少于自变量个数时进行回归建模;
- 最终模型中含原有所有自变量,回归系数容易解释。
- 计算简单、预测精度高,易于定性解释。
# 2.原理
典型相关分析(CCA)对特征的处理方式比较粗糙,用的是线性回归来,因此会存在线性回归的一些缺点。
多元线性回归的缺点: 当自变量的数量大于样本量的时候,解不出
PCA 的缺点:PCA只考虑了自变量的方差,然后选取方差最大的几个正交变量,可以用于解决共线性问题(计量),没有考虑自变量对因变量的贡献。
偏最小二乘回归分析在建模过程中集中了主成分分析,典型相关分析和线性回归分析方法的特点,因此在分析结果中,除了可以提供一个更为合理的回归模型外,还可以同时完成一些类似于主成分分析和典型相关分析的研究内容,提供更丰富、深入的一些信息。
对于 P 个因变量
# 3.适用情况
偏最小二乘回归是集【主成分分析】,【典型相关分析】和【多元线性回归分析】3种分析方法的优点于一身的方法。
多元线性回归的缺点: 当自变量的数量大于样本量的时候,解不出
,设 ,当 k>n 时, 的秩为n,不是满秩的,所以没有逆矩阵Rank(A,B)<=Rank(B) PCA的缺点:PCA只考虑了自变量的方差,然后选取方差最大的几个正交变量,可以用于解决共线性问题(计量),没有考虑自变量对因变量的贡献
PLS:偏最小二乘回归提供一种多对多线性回归建模的方法,特别当两组变量的个数很多,且都存在多重相关性,而样本又比较少的时候
# 4.计算步骤
先将 X 与 Y 标准化:
第一步:
分别提取两组 X 与 Y 变量的第一对成分
为了回归分析的需要,要求:
(1)
(2))
第二步:计算
最大化协方差,使得)
和 的相关程度达到最大,可以用得分向量) 和 的内积来计算:
采用拉格朗日乘数法,问题化为求单位向量
与 ,使 达到最大,问题求解只需计算 的特征值与特征向量,且M的最大特征值为 ,相应的特征向量就是所要求解的 ,进而也能得到
第三步
由两组变量集的标准化观察数据矩阵 X 和 Y,可以计算第一对成分的得分向量,记为
- 建立<
对 的回归及 对 的回归,假定回归模型:
其中,
回归系数
的最小二乘估计为 用残差阵
代替 ,重复以上步骤,直到残差阵中元素的绝对值近似为0,每进行一次得到一个 。
第四步
重复上面的步骤,得到 r 个成分
将
第五步:交叉有效性检验
应该提取多个成分,可以使用交叉有效性检验,每次舍去第 i 个观察数据,对余下的 n-1个观测数据用最小二乘回归方法,并考虑抽取 h(h<=r) 个成分后拟合的回归式,然后把舍去的自变量组第 j 个观测数据代入所拟合的回归方程式,得到
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] Jong S D , Phatak A . Partial least squares regression[C]// International Workshop on Recent Advances in Total Least Squares Techniques & Errors-in-variables Modeling. Society for Industrial and Applied Mathematics, 1997.