岭回归(Ridge)

操作视频

# 岭回归

# 1、作用

岭回归(Ridge regression),也叫L2正则化（L2 regularization），是一种专用于共线性（即自变量之间高度相关）数据分析的有偏估计回归方法，用于研究变量之间的关系以及估计因变量基于自变量的变化情况。它通过引入L2范数惩罚项来约束模型复杂度，从而降低了模型过拟合的风险，提高了模型的泛化性能。岭回归实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数，对病态数据的拟合要强于最小二乘法。随着大数据时代海量数据的涌现，岭回归因其在稀疏性和稳定性方面的特性，在金融风险分析、生物医学数据分析、信号处理等领域得到广泛应用。

# 2、输入输出描述

输入:自变量X至少包括一项或以上的定量变量，如果自变量中包含二分类定类变量（如性别、是否等），需要将这些变量转换为哑变量（dummy variables），每个二分类变量转换为至少一个哑变量，通常用0和1表示不同的类别。因变量Y必须是定量变量，如果因变量是定类变量，则应考虑使用逻辑回归或其他适当的分类模型。
输出:模型检验优度的结果，自变量对因变量的线性关系等等。

# 3、案例示例

案例:通过自变量（房间面积、楼层高度、房子单价、是否有电梯、周围学校数量、距地铁站位置）拟合预测因变量（房价），现在发现房子单价与楼层高度之间有着很强的共线性，VIF 值高于 20；不能使用常见的最小二乘法 OLS 回归分析，需要使用岭回归模型。

# 4、案例数据

岭回归案例数据

# 5、案例操作

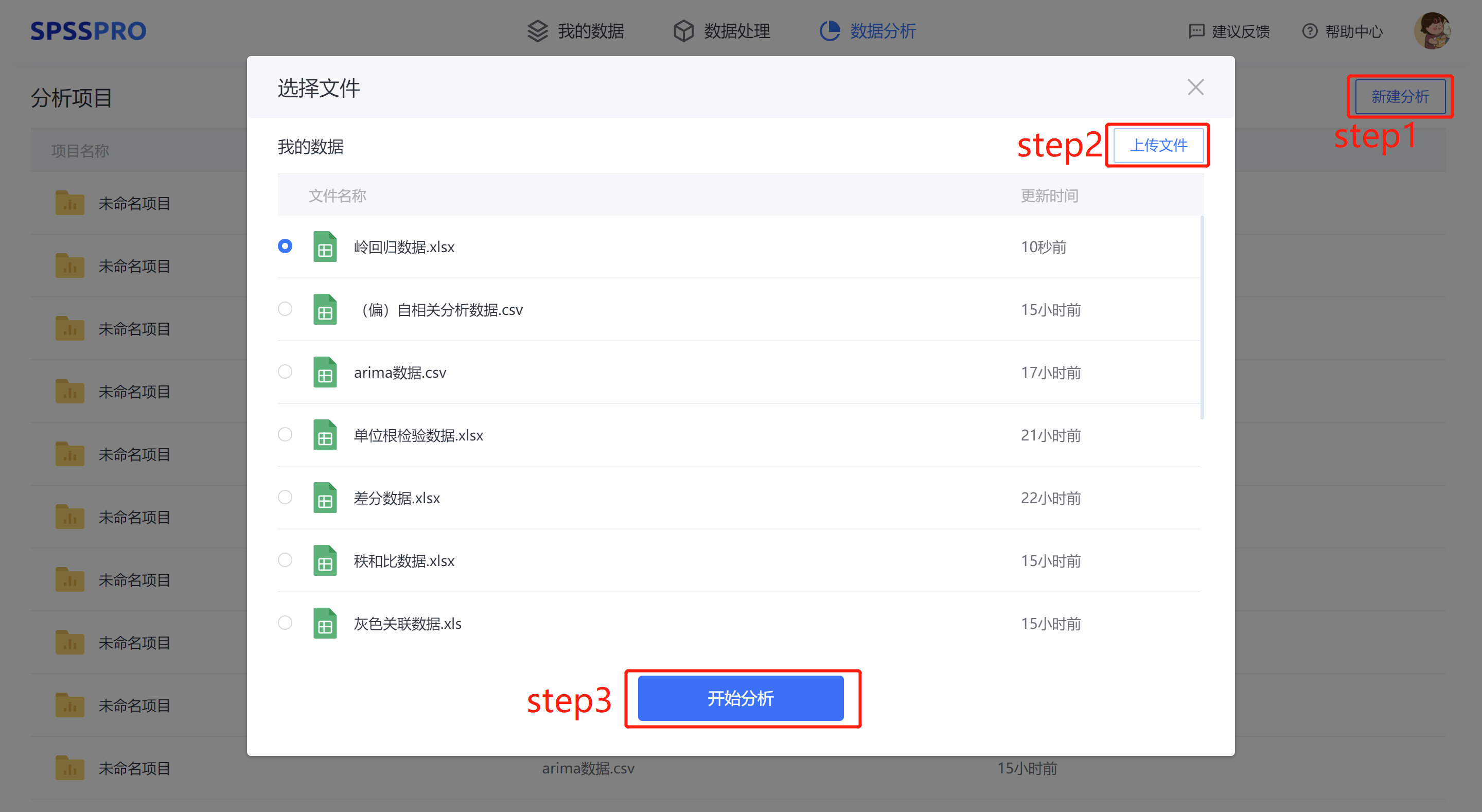
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；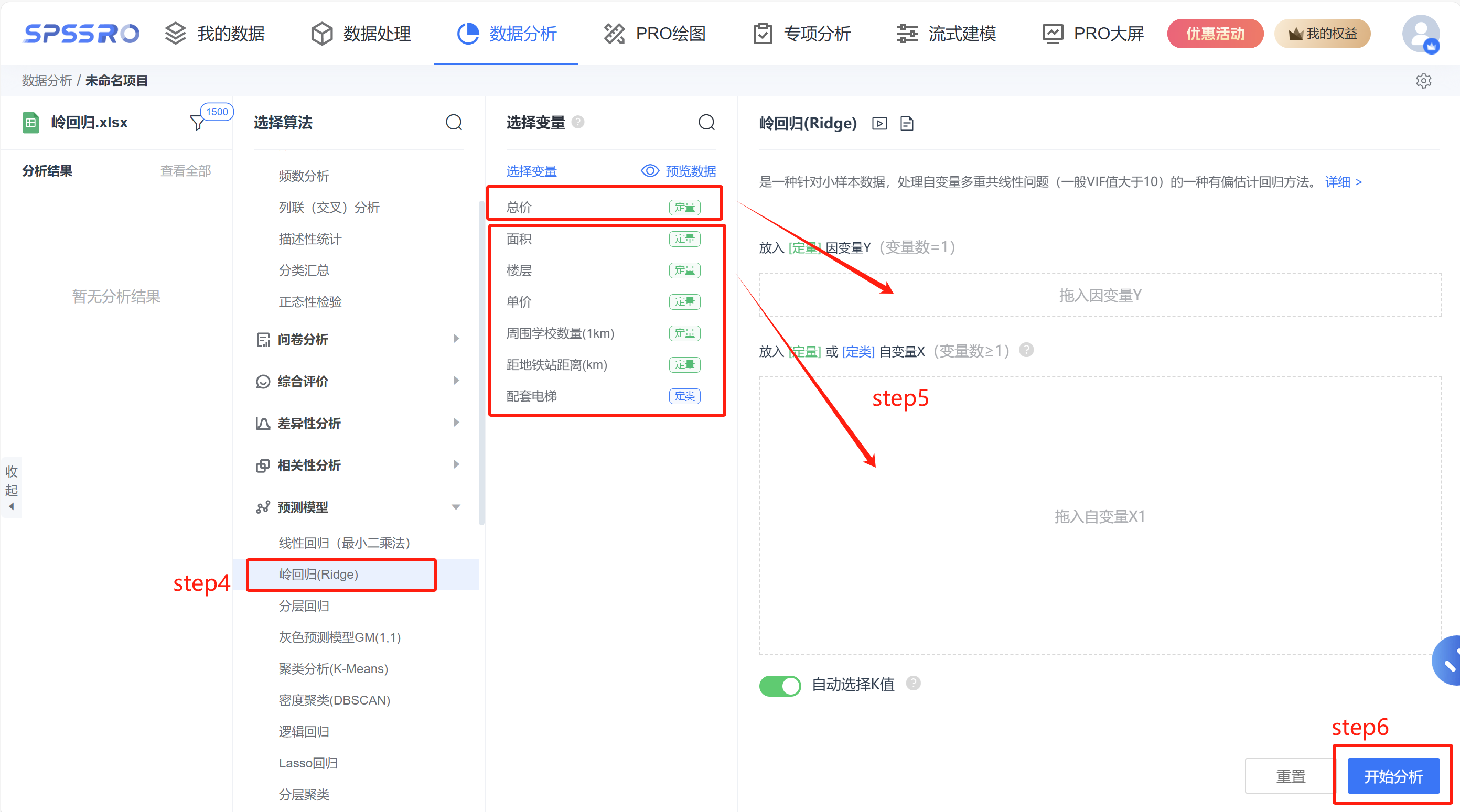

step4：选择【岭回归（Ridge）】；
step5：查看对应的数据数据格式，【岭回归（Ridge）】要求自变量 X 至少一项或以上的定量变量或二分类定类变量，因变量 Y 要求为定量变量；
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：岭迹图

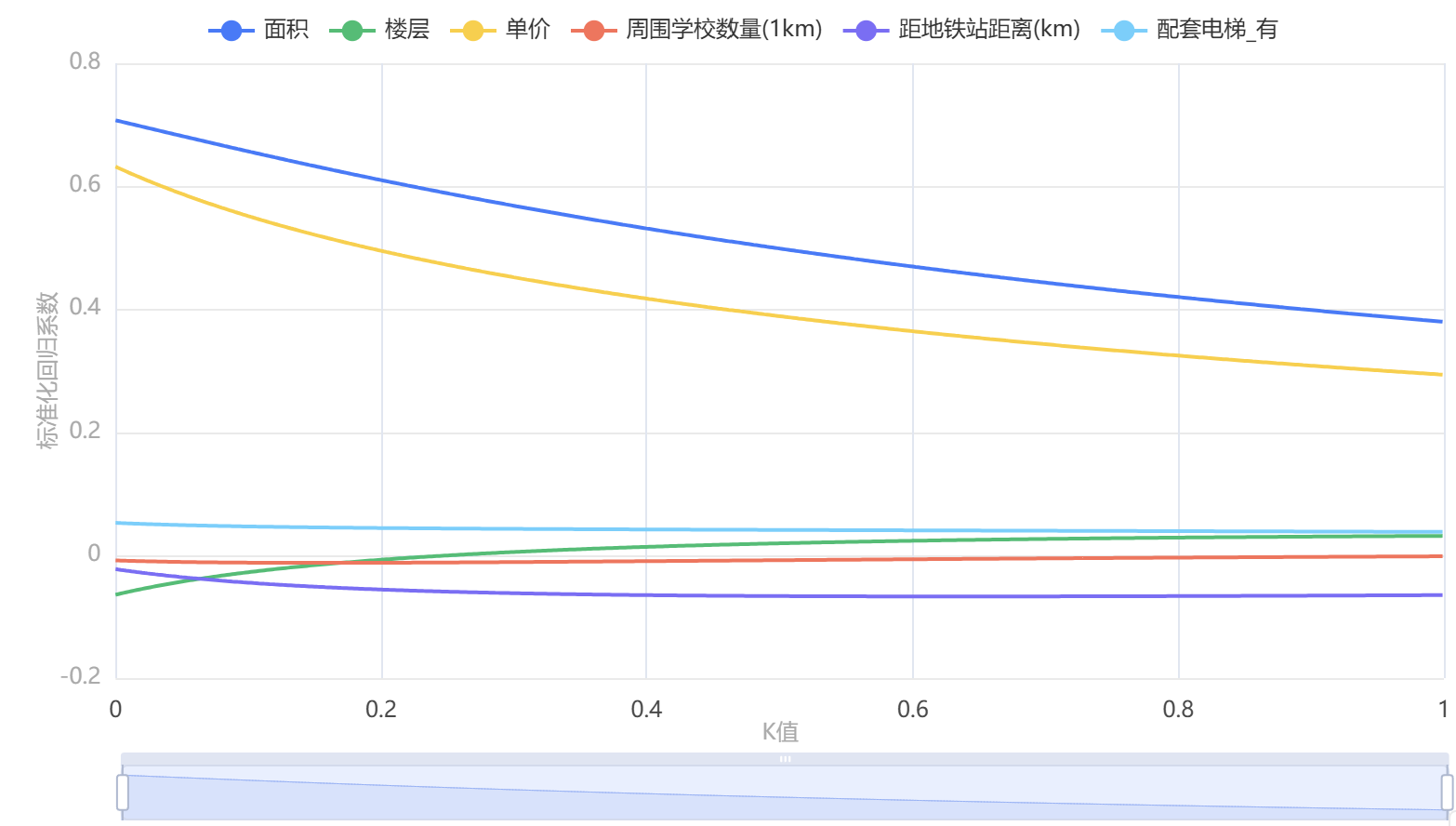
图表说明:上图以可视形式化展示了本次模型的各个自变量的标准化系数趋于稳定时的情况。智能分析：根据方差扩大因子法确定K=0.162

输出结果 2：岭回归分析结果

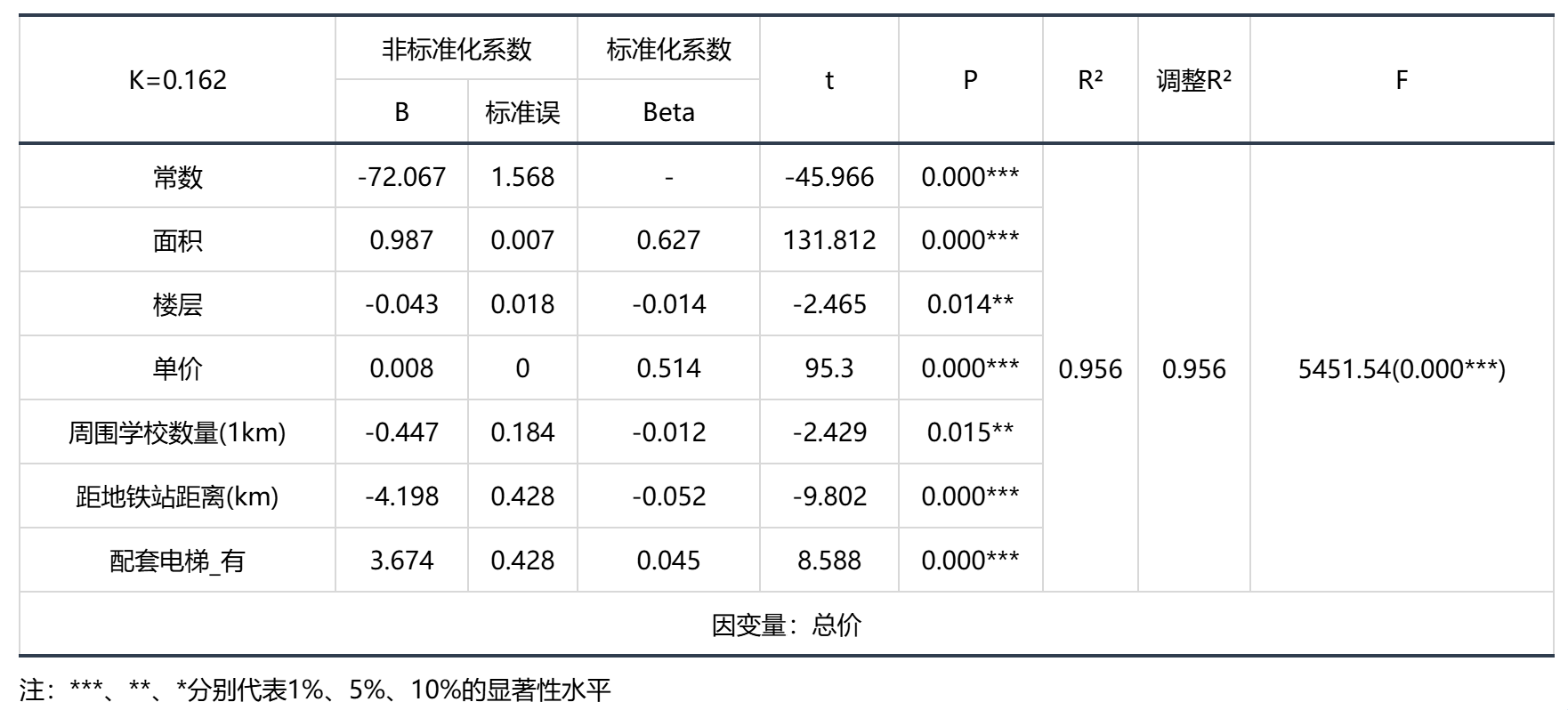
图表说明: 上表格展示了本次模型的参数结果及检验结果，包括模型的标准化系数、t值、F检验的结果、R²、调整R²等，用于模型的检验，并分析模型的公式。
● 曲线回归模型要求总体的回归系数不为0，即变量之间存在回归关系。根据F检验的P值对模型进行检验。
智能分析：岭回归的结果显示：基于F检验显著性P值为0.000***，水平上呈现显著性，拒绝原假设，表明自变量与因变量之间存在着回归关系。同时，模型的拟合优度R²为0.963，模型表现为较为较为优秀。
模型的公式：总价=-72.067＋0.987 × 面积-0.043 × 楼层＋0.008 × 单价-0.447 × 周围学校数量(1km)-4.198 × 距地铁站距离(km)＋3.674 ×

配 套 电 梯_{有}

输出结果 3：模型路径图 

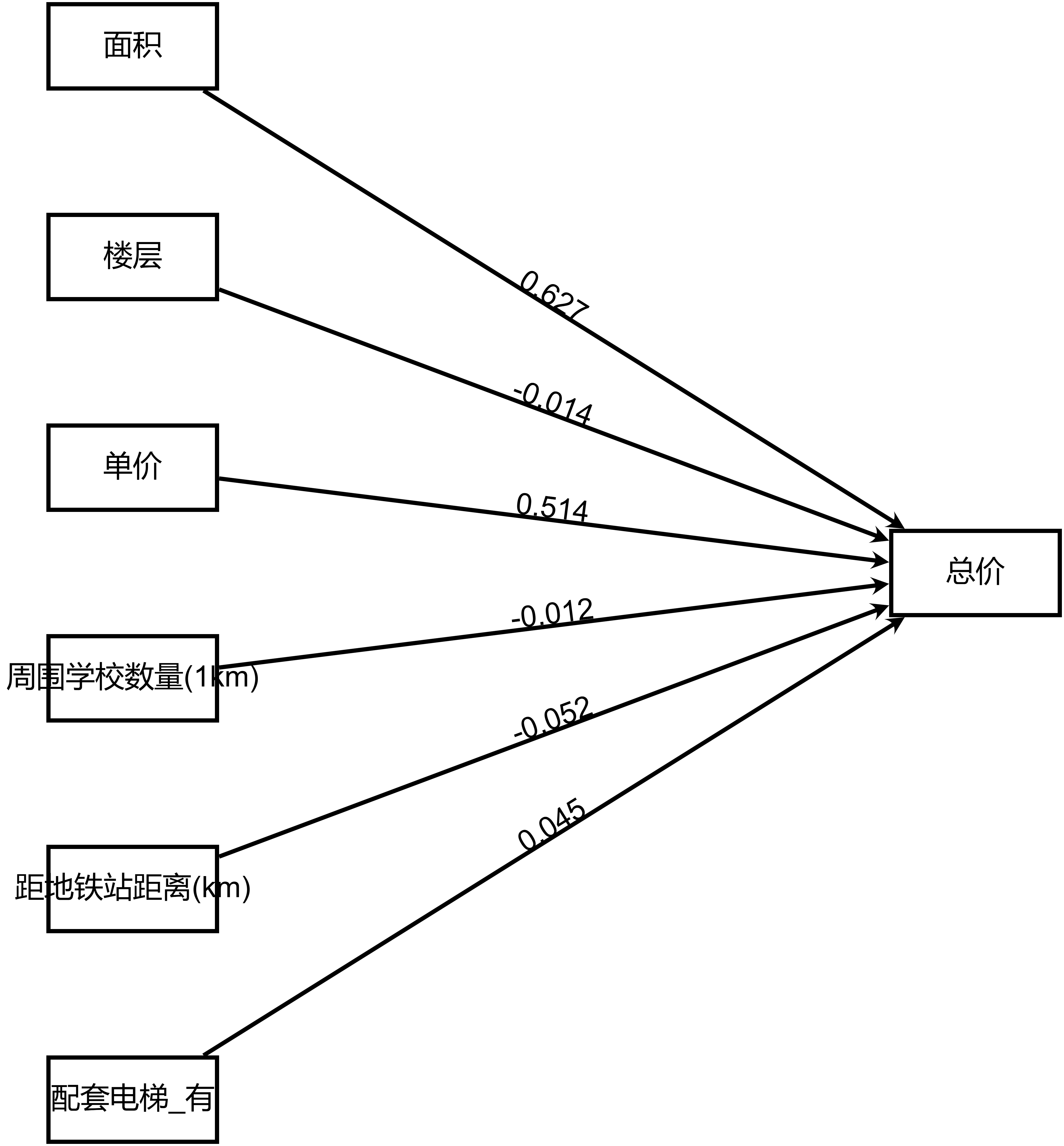
图表说明:上图以路径图形式展示了本次模型结果，主要包括模型的系数，用于分析模型的公式。

输出结果 4：模型结果图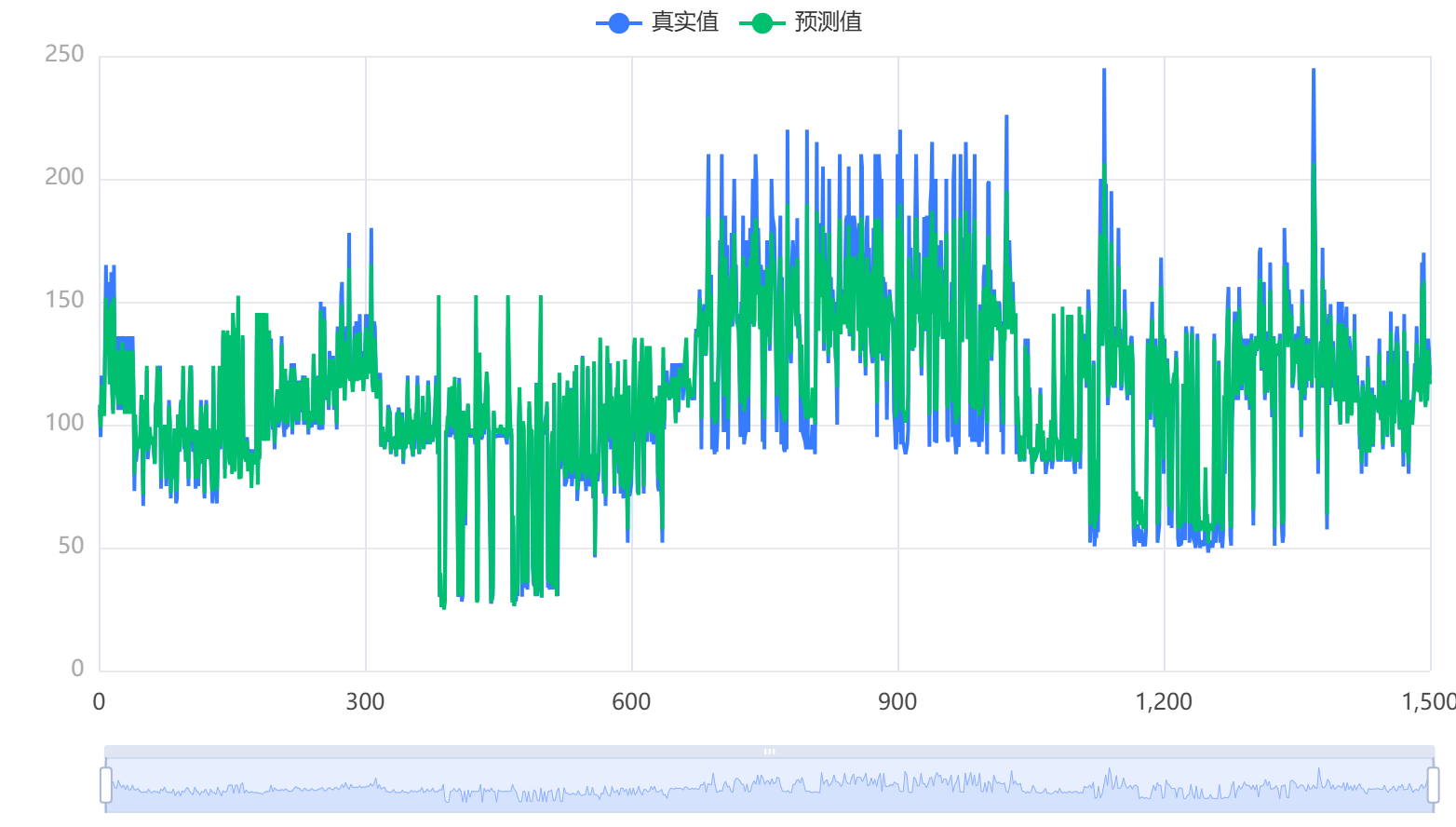

图表说明:上图以可视化的形式展示了本次模型的原始数据图、模型拟合值。

输出结果 5：模型结果预测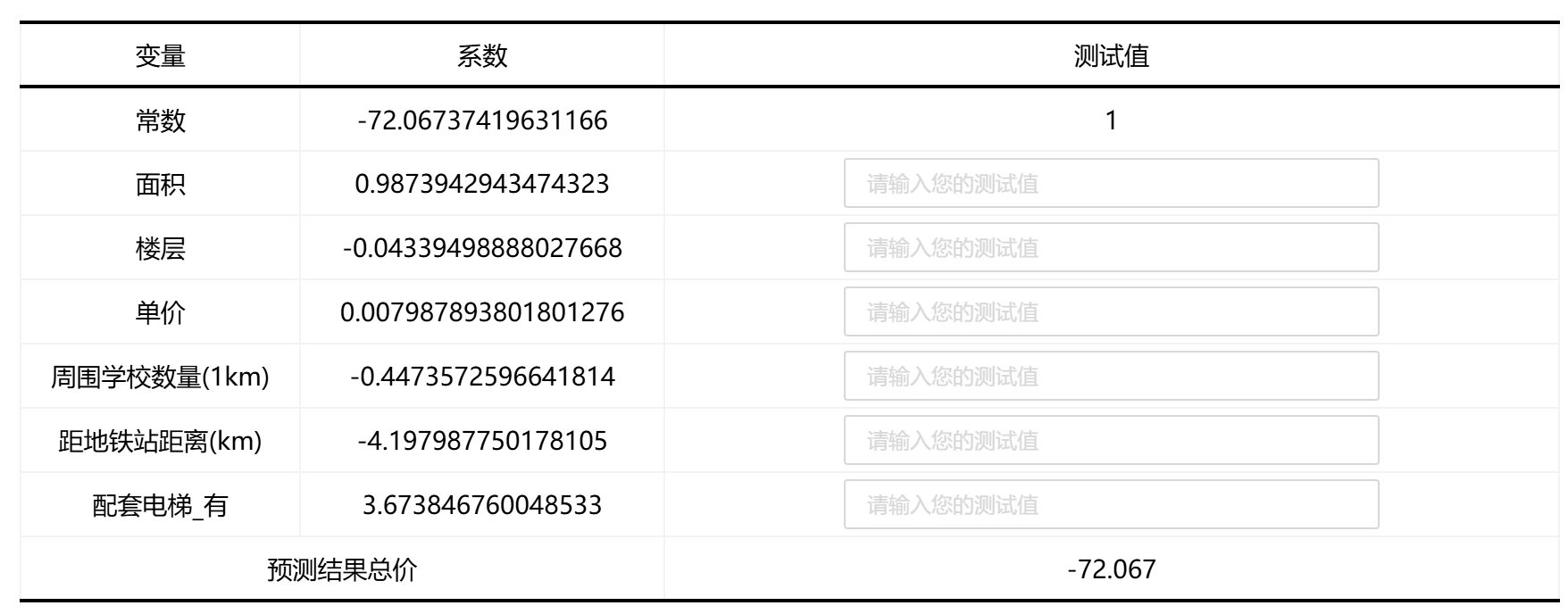

图表说明:上表格用于对岭回归模型的进行预测。

# 7、注意事项

一般在做岭回归之前，先采用线性回归（最小二乘法回归），如果发现自变量 VIF（共线性）过大，如超过 10，才使用岭回归；
SPSSPRO 采用方差扩大因子法来自动寻找 K 值；
选取 k 值的一般原则是：
- 各回归系数的岭估计基本稳定
- 用最小二乘法估计的符号不合理的回归系数，其岭估计的符号变得合理
- 回归系数没有不合乎经济意义的绝对值
- 残差平方和增加不太多

# 8、模型理论

岭回归（Ridge Regression）是回归方法的一种，属于统计方法，在机器学习中也称作权重衰减，也有人称之为 Tikhonov 正则化或L2正则化。岭回归不进行特征选择，所以它不能通过消除特征来减少模型复杂性，但是，如果一个或多个特征对模型的输出影响过大，岭回归可以通过L2惩罚项来缩小模型中高的特征权重（即系数）。这样可以降低模型的复杂性，使模型的预测不那么过度依赖任何一个或多个特征。

岭回归主要解决的问题是两种：

当预测变量的数量超过观测变量的数量的时候（预测变量相当于特征，观测变量相当于样本），即数据点少于特征变量个数。

当输入的数据特征数比样本点还多时，意味着此时输入数据的矩阵 $X$ 不是满秩矩阵，非满秩矩阵不可求逆，因此不能使用普通的线性回归来做预测。而岭回归在矩阵 $X^{T} X$ 中加入了一个 $λ I$ 使得矩阵非奇异，从而对 $X^{T} X + λ I$ 求逆。此时，回归系数的计算公式为：

\hat{w} = (X^{T} X + λ I)^{- 1} X^{T} y

其中， $I$ 是一个单位方阵。这里通过引入 $λ$ 来限制所有 $w$ 的和，从而能够减少不重要的参数，在统计学上，这叫系数缩减（coefficient shrinkage）。

数据集之间具有多重共线性，即预测变量之间具有相关性。

一般的，回归分析的（矩阵）形式如下：

一般情况下，使用最小二乘法求解上述回归问题的目标是最小化如下的式子：

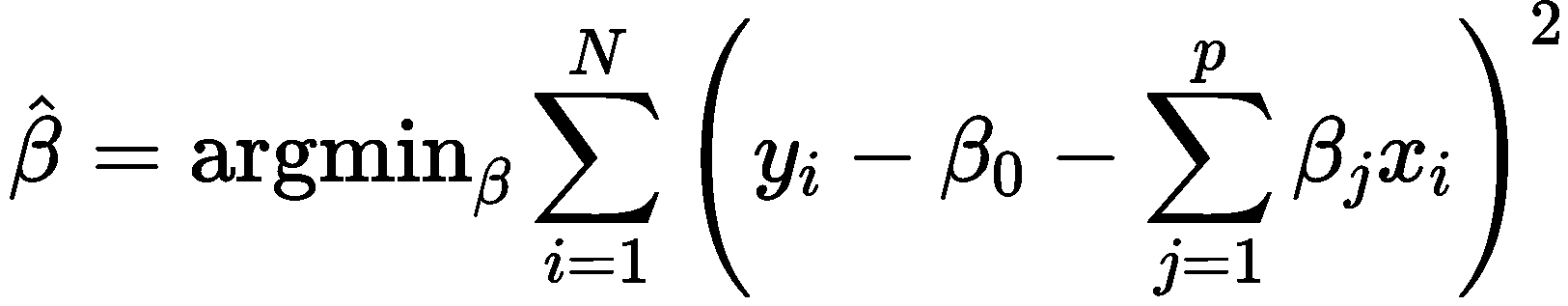
岭回归就是要在上述最小化目标中加上一个惩罚项：

L 2 = | | B | |^{2} = B_{1}^{2} + B_{2}^{2} + . . . + B_{n}^{2}

$L 2$ 惩罚项被插入到函数末尾，形成新的形式，即岭回归估计器（ridge regression estimator），其中，它对模型的影响由超参数 $λ$ 控制：

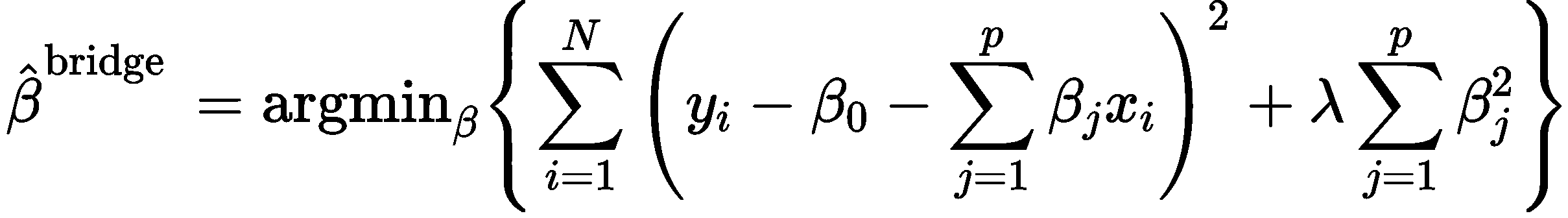
这里的λ也是待求参数，也就是说，岭回归是带二范数惩罚的最小二乘回归。

请注意，岭回归并不会以相同的幅度收缩每个系数，相反，系数的收缩程度与其初始大小成比例，随着 λ 的增加，初始值较高的系数将比初始值较低的系数更快地收缩。因此，高数值的系数受到的惩罚也比低数值的系数更大。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 刘超,回归分析——方法、数据与 R 的应用,高等教育出版社,2019
[3] Jacob Murel Ph.D., Eda Kavlakoglu.What is ridge regression?.2023(11). Retrieved from: https://www.ibm.com/topics/ridge-regression

建议反馈