线性回归（最小二乘法）

操作视频

# 线性回归（最小二乘法）

# 1、作用

线性回归(最小二乘法)是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，在线性回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。

# 2、输入输出描述

输入:自变量X至少包括一项或以上的定量变量，如果自变量中包含二分类定类变量（如性别、是否等），需要将这些变量转换为哑变量（dummy variables），每个二分类变量转换为至少一个哑变量，通常用0和1表示不同的类别。因变量Y必须是定量变量，如果因变量是定类变量，则应考虑使用逻辑回归或其他适当的分类模型。
输出:模型检验优度的结果，自变量对因变量的线性关系等等。

# 3、案例示例

示例：通过自变量（房子年龄、是否有电梯、楼层高度、房间平方）拟合预测因变量（房价）

# 4、案例数据

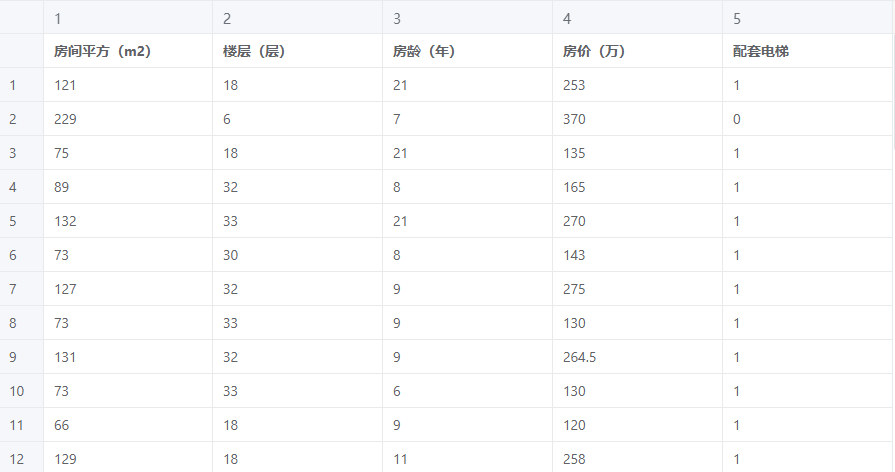
线性回归案例数据

# 5、案例操作

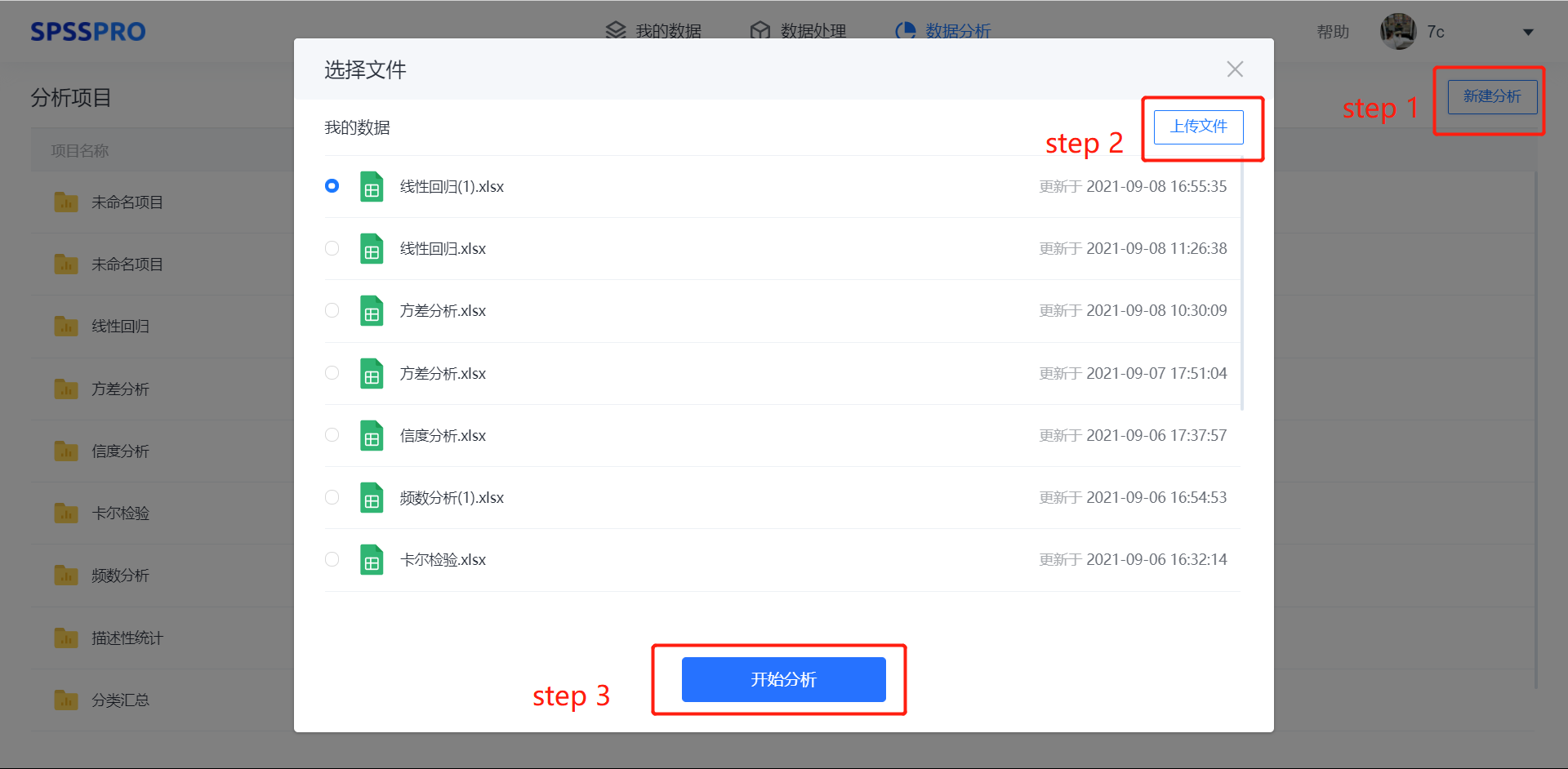
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；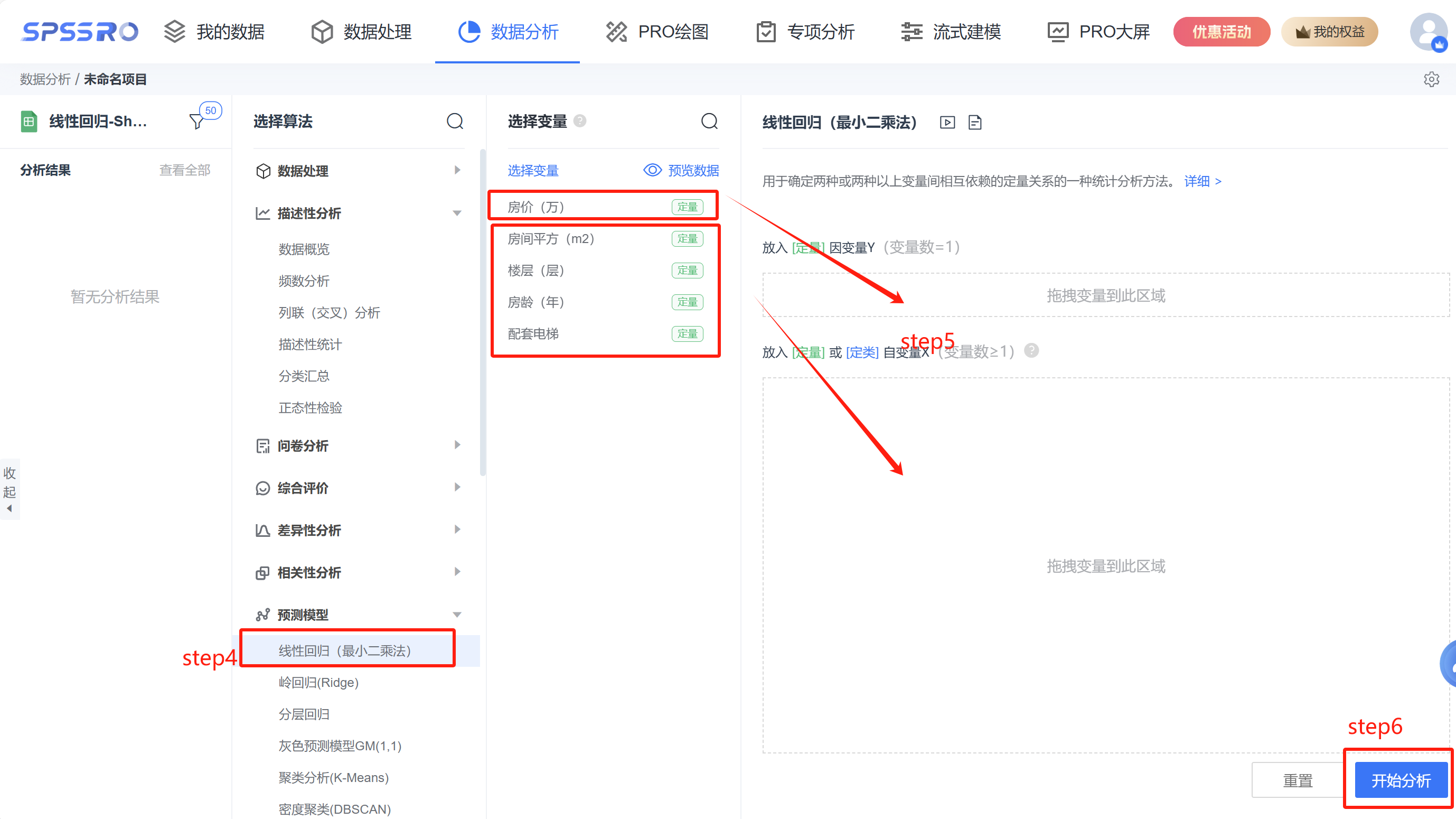
step4：选择【线性回归（最小二乘法）】；
step5：查看对应的数据数据格式，按要求输入【线性回归（最小二乘法）】数据;
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：线性回归分析结果表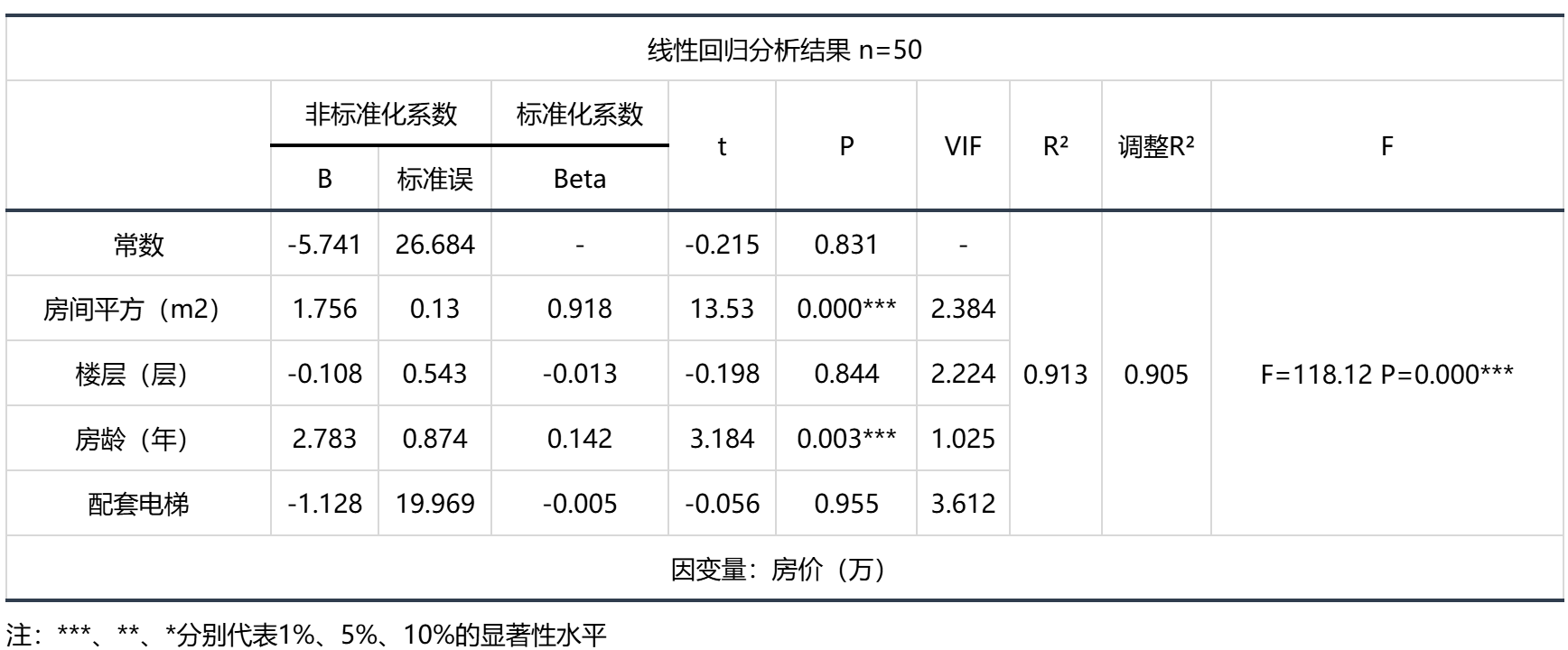
图表说明：上表格展示了本次模型的分析结果，包括模型的标准化系数、t值、VIF值、R²、调整R²等，用于模型的检验，并分析模型的公式。

线性回归模型要求总体回归系数不为0，即变量之间存在回归关系。根据F检验结果对模型进行检验。
R²代表曲线回归的拟合程度，越接近1效果越好。
VIF值代表多重共线性严重程度，用于检验模型是否呈现共线性，即解释变量间存在高度相关的关系（VIF应小于10或者5，严格为5）若VIF出现inf，则说明VIF值无穷大，建议检查共线性，或者使用岭回归。
B是有常数情况下的的系数。
标准误=B/t值。
标准化系数是将数据标准化后得到的系数。
VIF是共线性。
F(df1,df2)是df1等于自变量数量；df2等于样本量-(自变量数量+1)。
F检验是为了判断是否存在显著的线性关系，R²是为了判断回归直线与此线性模型拟合的优劣。在线性回归中主要关注F检验是否通过，而在某些情况下R²大小和模型解释度没有必然关系。

智能分析： F检验的结果分析可以得到，显著性P值为0.000***，水平上呈现显著性，拒绝回归系数为0的原假设，因此模型基本满足要求。对于变量共线性表现，VIF全部小于10，因此模型没有多重共线性问题，模型构建良好。
模型的公式如下：y=-5.741 + 1.756房间平方（m2） - 0.108楼层（层） + 2.783房龄（年） - 1.128配套电梯。

输出结果 2：拟合效果图

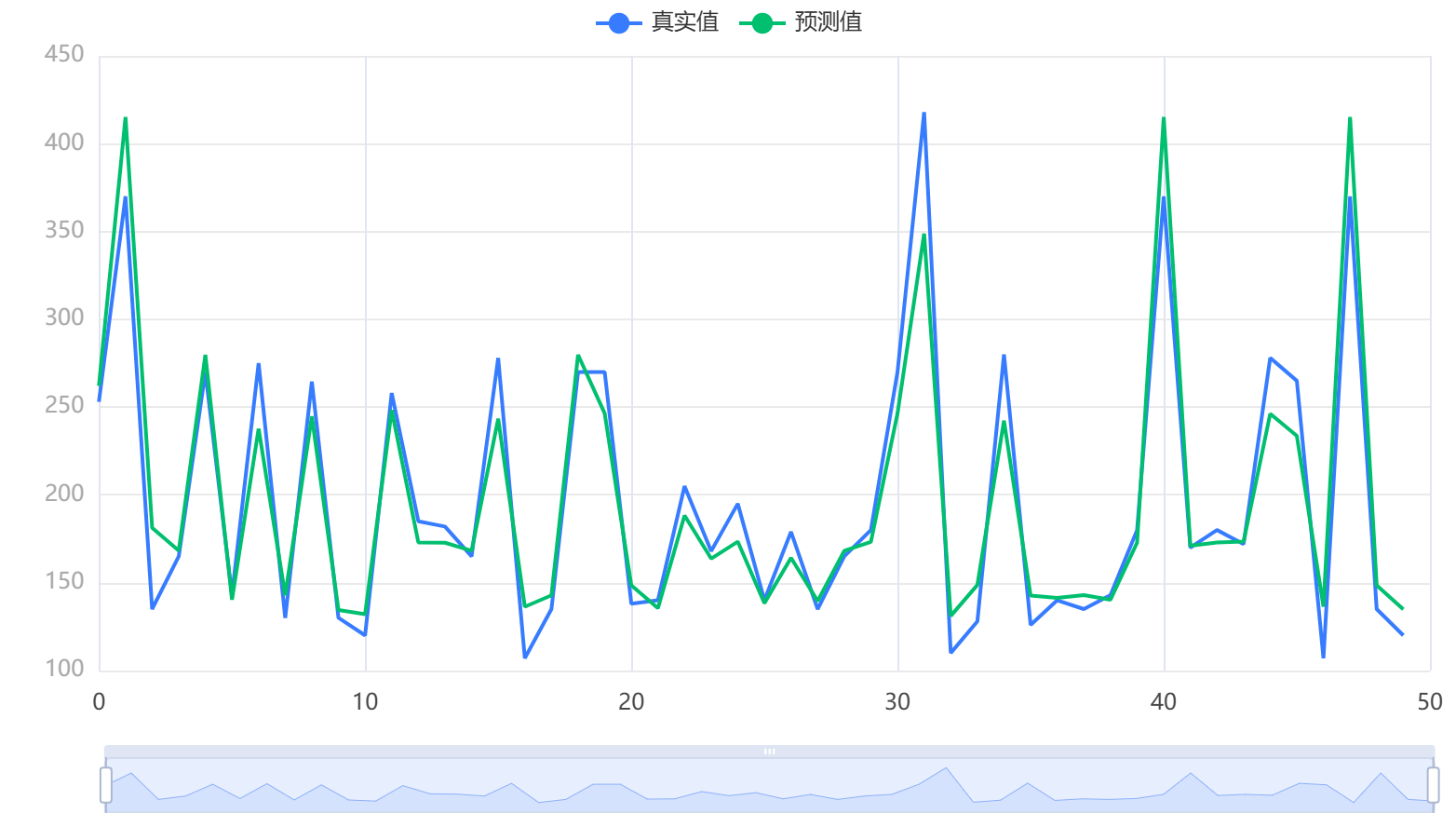
图表说明:上图展示了本次模型的原始数据图、模型拟合值、模型预测值。

输出结果 3：模型路径图

图表说明:上图以路径图形式展示了本次模型结果，主要包括模型的系数，用于分析X对于Y的影响关系情况。

输出结果 4：模型结果预测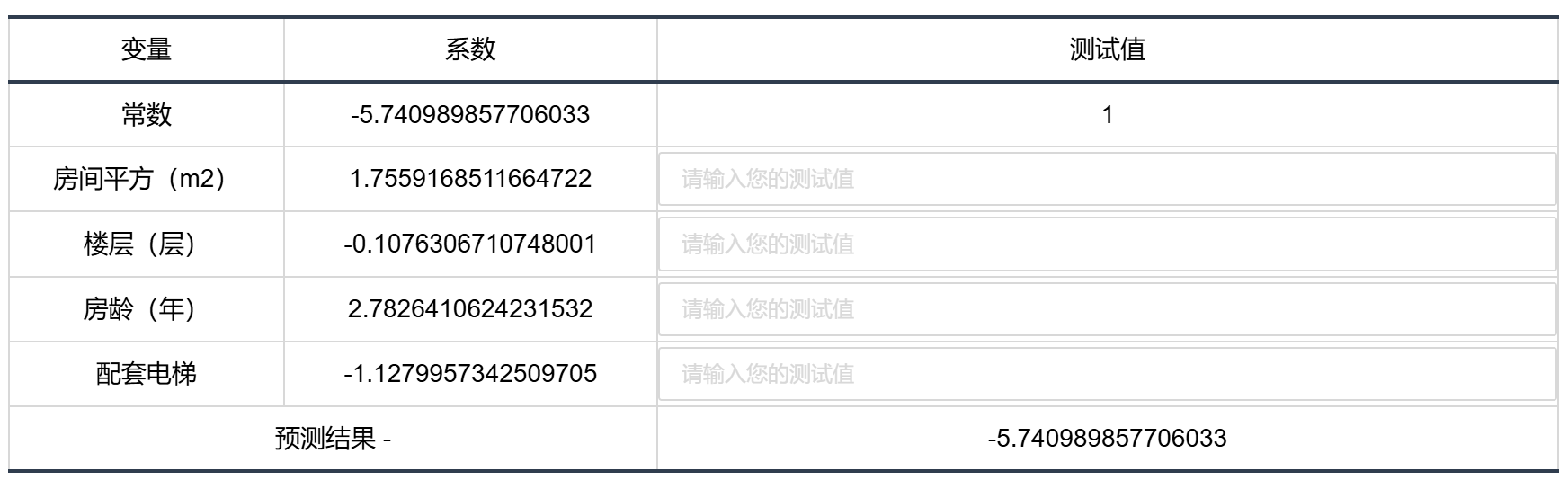

图表说明:上表格显示了线性回归模型的预测情况。

# 7、注意事项

计算方法与差异：线性回归模型的参数可以通过多种方法求解，其中最小二乘法和梯度下降法是两种常见的方法。SPSSPRO 采用最小二乘法来计算线性回归的参数，这种方法在结果上与 SPSS 软件通常是一致的，但需要注意的是，由于梯度下降法依赖于初始值的选择和迭代过程，因此其最终得到的参数值可能与最小二乘法存在细微的差异。
定类数据的处理：在线性回归模型中，如果输入变量中包含定类数据，这些数据需要被适当地处理以用于回归分析。SPSSPRO 要求，如果输入变量是定类数据，那么这些定类数据必须是二分类的，或者它们需要被转换为哑变量形式；如果输入的定类数据不是二分类的，SPSSPRO 会自动进行哑变量化处理，以确保数据可以被正确地用于线性回归模型。

# 8、模型理论

线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。其表达形式为 y = w'x+e，e 为误差服从均值为 0 的正态分布。
回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量，且因变量和自变量之间是线性关系，则称为多元线性回归分析。
一般来说，线性回归都可以通过最小二乘法或梯度下降法求出其方程，可以计算出对于 y=bx+a 的直线。以最小二乘法为例一般地，影响 y 的因素往往不止一个，假设有 x1，x2，...，xk，k 个因素，通常可考虑如下的线性关系式：

对 y 与 x1，x2，...，xk 同时作 n 次独立观察得 n 组观测值（xt1，xt2，...，xtk），t=1,2,...,n（n>k+1），它们满足关系式：

其中，

互不相关均是与

同分布的随机变量。为了用矩阵表示上式，令：

使用最小二乘法得到

的解

其中，

称为

的伪逆
斜率 b 计算方法
法 1：用

法 2：把斜率 b 带入

截距 a

# 9、手推步骤

# Step 1:矩阵构建

构造设计矩阵 $X$ 和因变量向量 $Y$ :
$X$ 矩阵包含常数项和4个自变量，维度为 $50 \times 5$ ：

$X = [\begin{matrix} 1 & x_{11} & x_{12} & x_{13} & x_{14} \\ 1 & x_{21} & x_{22} & x_{23} & x_{24} \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 1 & x_{50, 1} & x_{50, 2} & x_{50, 3} & x_{50, 4} \end{matrix}]$
$Y$ 向量维度为 $50 \times 1$ ：

$Y = [\begin{matrix} y_{1} \\ y_{2} \\ ⋮ \\ y_{50} \end{matrix}]$

# Step 2:计算 $X^{T} X$ 和 $X^{T} Y$

计算各变量的总和及交叉项：
总和:

$\sum X_{1} = 6213, \sum X_{2} = 1167, \sum X_{3} = 589, \sum X_{4} = 43$
平方和与交叉积:

$\sum X_{1}^{2} = 838, 897, \sum X_{2}^{2} = 31, 007, \sum X_{3}^{2} = 8, 223, \sum X_{4}^{2} = 43$

$\sum X_{1} X_{2} = 145, 634, \sum X_{1} X_{3} = 76, 456, \sum X_{1} X_{4} = 5, 247$

$\sum Y = 13, 146, \sum X_{1} Y = 1, 733, 042, \sum X_{2} Y = 318, 567, \sum X_{3} Y = 164, 289, \sum X_{4} Y = 11, 307$
构造矩阵 $X^{T} X$ 和 $X^{T} Y$
$X^{T} X = [\begin{matrix} 50 & 6213 & 1167 & 589 & 43 \\ 6213 & 838, 897 & 145, 634 & 76, 456 & 5, 247 \\ 1167 & 145, 634 & 31, 007 & 15, 678 & 1, 043 \\ 589 & 76, 456 & 15, 678 & 8, 223 & 587 \\ 43 & 5, 247 & 1, 043 & 587 & 43 \end{matrix}]$ , $X^{T} Y = [\begin{matrix} 13, 146 \\ 1, 733, 042 \\ 318, 567 \\ 164, 289 \\ 11, 307 \end{matrix}]$

# Step 3:求逆矩阵 $(X^{T} X)^{- 1}$

通过矩阵分块法或高斯消元法计算逆矩阵：

$(X^{T} X)^{- 1} = [\begin{matrix} 0.019 & - 0.0001 & - 0.001 & 0.002 & - 0.025 \\ - 0.0001 & 0.00002 & 0.00001 & - 0.00003 & 0.0002 \\ - 0.001 & 0.00001 & 0.0001 & - 0.0002 & 0.001 \\ 0.002 & - 0.00003 & - 0.0002 & 0.0005 & - 0.003 \\ - 0.025 & 0.0002 & 0.001 & - 0.003 & 0.021 \end{matrix}]$

# Step 4:计算回归系数 $\hat{β}$

公式即计算过程如下：

$\hat{β} = (X^{T} X)^{- 1} X^{T} Y = [\begin{matrix} - 5.741 \\ 1.756 \\ - 0.108 \\ 2.783 \\ - 1.128 \end{matrix}]$

推导示例:

截距项 $β_{0}$
$β_{0} = 0.019 \times 13, 146 + (- 0.0001) \times 1, 733, 042 + (- 0.001) \times 318, 567 + 0.002 \times 164, 289 + (- 0.025) \times 11, 307 = - 5.741$
房间平方系数 $β_{1}$
$β_{1} = (- 0.0001) \times 13, 146 + 0.00002 \times 1, 733, 042 + 0.00001 \times 318, 567 + (- 0.00003) \times 164, 289 + 0.0002 \times 11, 307 = 1.756$
其余系数同理，逐项相乘累加。

# Step 5:计算标准误差

方法1：基于残差标准差 $σ$
1)计算残差平方和 $S S E$

$S S E = \sum (y_{i} - {\hat{y}}_{i})^{2} = \sum y_{i}^{2} - {\hat{β}}^{T} X^{T} Y = 3, 678, 912 - (- 5.741 \times 13, 146 + 1.756 \times 1, 733, 042 - 0.108 \times 318, 567 + \dots) \approx 1, 283.5$

2)残差标准差 $σ$

$σ = \sqrt{\frac{S S E}{n - k - 1}} = \sqrt{\frac{1, 283.5}{50 - 4 - 1}} \approx 5.12$

3)系数标准误差

$u (b_{j}) = σ \cdot \sqrt{(X^{T} X)_{j j}^{- 1}}$

房间平方的标准误差：

u (b_{1}) = 5.12 \times \sqrt{0.00002} \approx 0.13

方法2：直接代入公式
以房间平方为例：
计算 $S_{x x}$ 和 $S_{x y}$ :

$S_{x x} = \sum x_{1 i}^{2} - \frac{(\sum x_{1 i})^{2}}{n} = 838, 897 - \frac{6213^{2}}{50} \approx 14, 500$

$S_{x y} = \sum x_{1 i} y_{i} - \frac{\sum x_{1 i} \sum y_{i}}{n} = 1, 733, 042 - \frac{6213 \times 13, 146}{50} \approx 25, 400$

标准误差:

$u (b) = \sqrt{\frac{\frac{S_{x y}^{2}}{S_{x x}} - b^{2}}{n - 2}} = \sqrt{\frac{\frac{25, 400^{2}}{14, 500} - {1.756}^{2}}{48}} \approx 0.13$

# Step 6. 模型评估统计量

总平方和 $S S T$ ：

$S S T = \sum (y_{i} - \bar{y})^{2} = \sum y_{i}^{2} - \frac{(\sum y_{i})^{2}}{n} = 3, 678, 912 - \frac{13, 146^{2}}{50} \approx 14, 800$

判定系数 $R^{2}$ ：

$R^{2} = 1 - \frac{S S E}{S S T} = 1 - \frac{1, 283.5}{14, 800} \approx 0.913$

调整 $R^{2}$ ：

$调整 R^{2} = 1 - \frac{(1 - R^{2}) (n - 1)}{n - k - 1} = 1 - \frac{(1 - 0.913) \times 49}{45} \approx 0.905$

$F$ 统计量：

$F = \frac{S S R / k}{S S E / (n - k - 1)} = \frac{(14, 800 \times 0.913) / 4}{1, 283.5 / 45} \approx 118.12$

最终模型公式:

$房价（万） = - 5.741 + 1.756 \cdot 房间平方（m²） - 0.108 \cdot 楼层（层） + 2.783 \cdot 房龄（年） - 1.128 \cdot 配套电梯（0/1）$

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]Cohen, J., Cohen P., West, S.G., & Aiken, L.S. Applied multiple regression/correlation analysis for the behavioral sciences. Hillsdale, NJ: Lawrence Erlbaum Associates. 2003.
[3]Draper, N.R. and Smith, H. Applied Regression Analysis. Wiley Series in Probability and Statistics. 1998.
[4]孙荣恒．应用数理统计（第三版）．北京：科学出版社，2014：204-206
[5]alton, Francis. Regression Towards Mediocrity in Hereditary Stature (PDF). Journal of the Anthropological Institute. 1886, 15: 246–263

建议反馈