有序逻辑回归

操作视频

# 1、作用

有序逻辑回归（Ordinal Logistic Regression）是一种用于分析有序因变量与自变量之间关系的统计方法，当因变量是具有自然顺序的类别（如等级、程度或满意度水平）时，有序逻辑回归特别适用。这种模型能够捕捉因变量类别之间的顺序信息，比简单的多类别逻辑回归更加适合处理有序分类数据。有序逻辑回归的主要目的是：

研究有序分类因变量与多个自变量之间的关系。
估计自变量对因变量等级变化的影响方向和强度。
预测个体属于哪个有序类别或评估个体在不同类别之间的概率。

# 2、输入输出描述

输入：自变量X可以为定量数据，也可以是定类数据，如果定类数据纳入模型，需要先将其设为哑变量，因变量Y为有序定类变量，若是用数值来代替各分类水平，可放入定量变量。
输出：有序逻辑回归系数估计以及分类预测的效果评价。

# 3、案例示例

案例：研究者想了解锻炼情况与肥胖水平的关系，为避免性别因素对结论的混杂影响，研究者将性别也纳入分析。

# 4、案例数据

有序逻辑回归案例数据

# 5、案例操作

Step1：新建项目；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

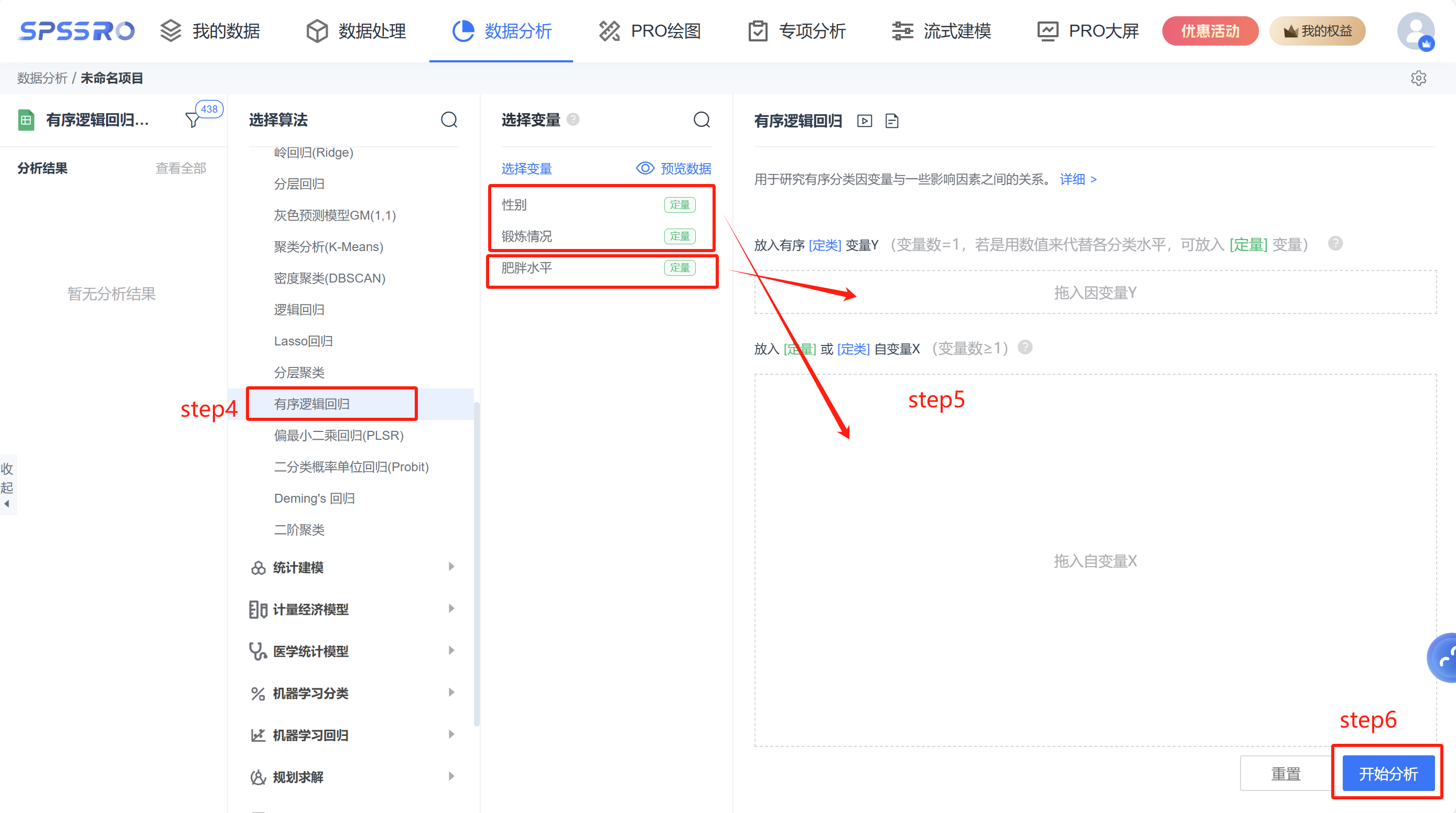
step4：选择【有序逻辑回归】；
step5：查看对应的数据数据格式，【有序逻辑回归】要求输入数据；
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果1：有序分类因变量基本汇总

因变量	选项	频数	百分比（%）
肥胖水平	1	99	22.603
	2	116	26.484
	3	114	26.027
	4	109	24.886
	总计	438	100.0

图表说明：图表说明：上表展示了因变量各分组的分布情况。
● 选项：当前字段数据下的去重类别。
● 频数：当前去重类别在数据中出现的次数。
● 百分比：当前变量的频数占比。
● 当因变量分类水平的数据量出现严重不平衡时，建议对数据进行过采样或者欠采样。

输出结果2：模型评价

似然比卡方	p	AIC	BIC
48.578	0.000***	1174.212	1194.624
注：*、、*分别代表1%、5%、10%的显著性水平

图表说明：上表展示了模型评价指标，可用于对模型的表现进行评估或有效性进行验证，其包括似然比检验，p值，AIC值、BIC值。
● 对p值进行分析，如果该值小于0.05，则说明模型有效；反之则说明模型无效。
● AIC 值和BIC 值用于对比两个模型的优劣时使用，此两个值均为越小越好。

分析：模型的似然比卡方检验的结果显示，显著性𝑝值0.000***，水平上呈现显著性，拒绝原假设，因而模型是有效的。

输出结果3：有序逻辑回归结果

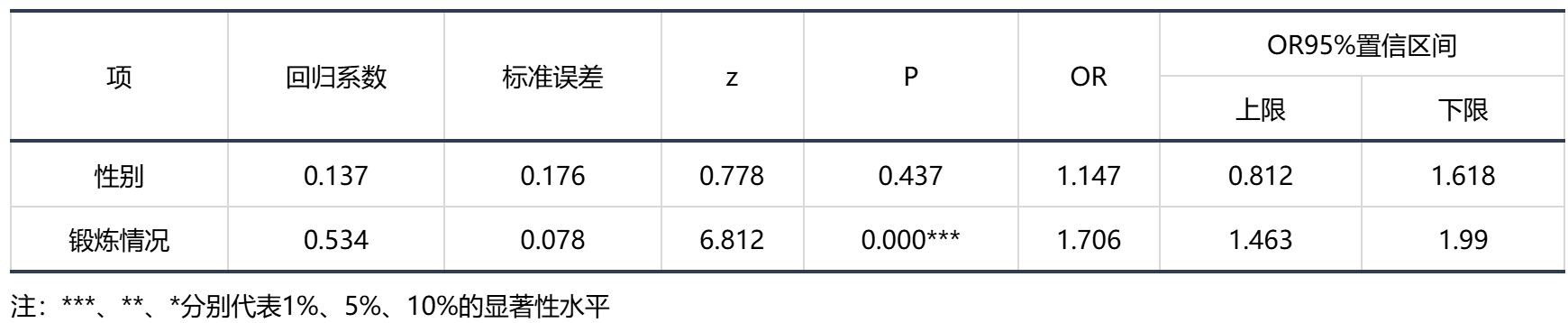
图表说明：上表展示了模型的参数结果，可用于生成模型公式。包括模型的系数、标准误差、OR值、置信区间等。
● OR值（优势比）：有序因变量等于及高于某等级的概率/有序因变量低于某等级的概率。
1、对于连续自变量的OR值的意义为：该变量每升高一个单位，有序因变量提高一个或一个以上等级的概率变化了（OR值-1）*100%。
2、对于哑变量化的0-1分类自变量的OR值意义为：该变量每升高一个单位（即分类水平从0变为1），有序因变量提高一个或一个以上等级的概率变化了（OR值-1）*100%。

分析：基于变量-性别，显著性P值为0.437，水平上不呈现显著性，不能拒绝原假设，因此性别对肥胖水平不会产生显著性影响。
基于变量-锻炼情况，显著性P值为0.000***，水平上呈现显著性，拒绝原假设，因此锻炼情况对肥胖水平会产生显著性影响，以及OR值为1.706，意味着锻炼情况每增加一个单位，肥胖水平提高一个或一个以上的等级的概率增加了70.641%。

输出结果4：因变量分类阈值

肥胖水平	1	2	3	4
预测值y	y ≤ 0.094	0,。094 < y ≤ 1.39	1.39 < y ≤ 2.631	2.631 < y

图表说明：上表展示了因变量分类阈值。若因变量预测值 ŷ 满足某个类别下方对应的表达式，那么样本就被预测为该类别。

输出结果5：混淆矩阵热力图

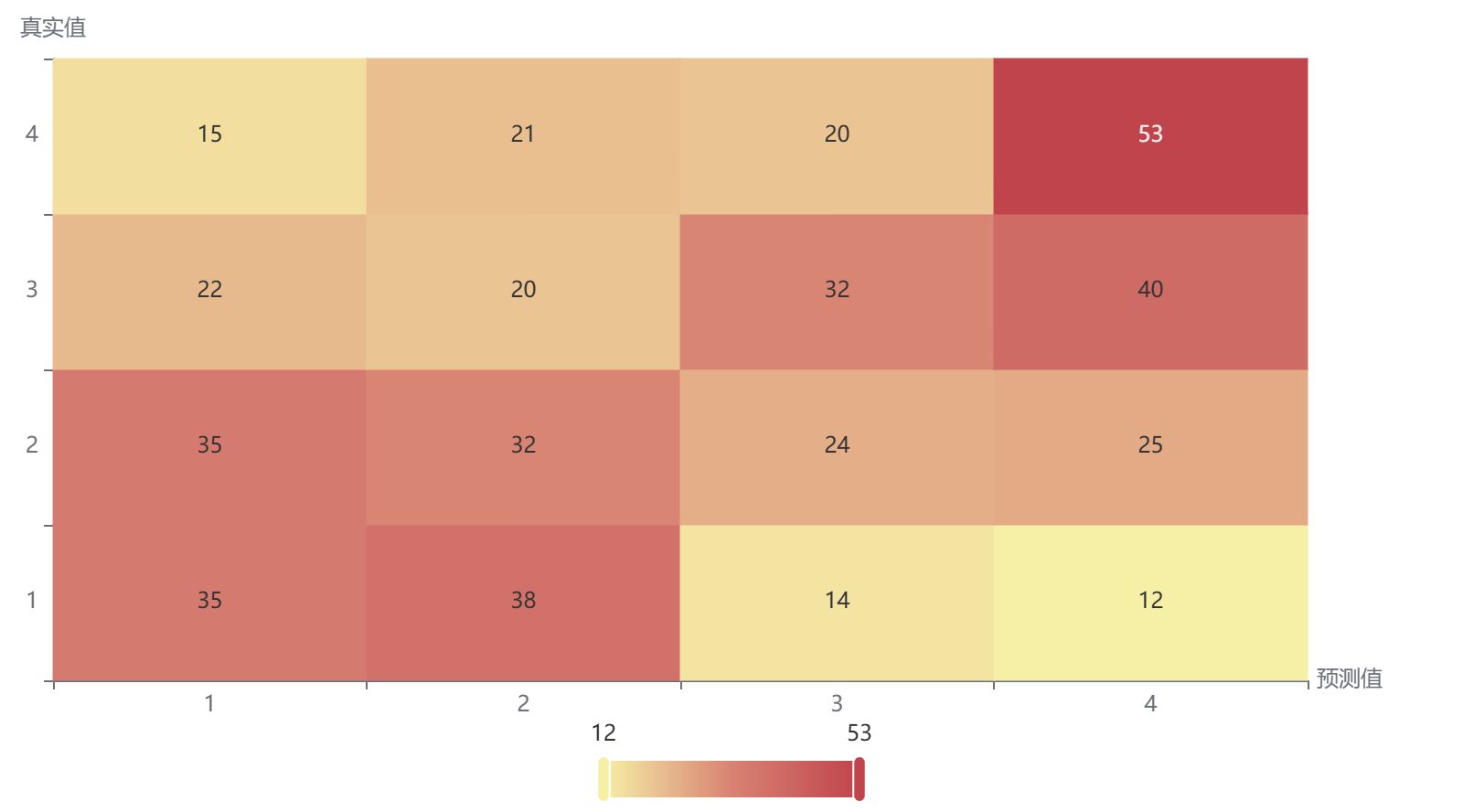
图表说明：上图以热力图的形式展示了混淆矩阵。

输出结果6：分类评价指标

准确率	召回率	精确率	F1	AUC
0.347	0.349	0.345	0.345	0.621

图表说明：上表中展示了分类评价指标，进一步通过量化指标来衡量逻辑回归的分类效果。
准确率：预测正确样本占总样本的比例，准确率越大越好。
召回率：实际为正样本的结果中，预测为正样本的比例，召回率越大越好。
精确率：预测出来为正样本的结果中，实际为正样本的比例，精确率越大越好。
F1：精确率和召回率的调和平均，精确率和召回率是互相影响的，虽然两者都高是一种期望的理想情况，然而实际中常常是精确率高、召回率就低，或者召回率低、但精确率高。若需要兼顾两者，那么就可以用F1指标。
AUC：AUC值越接近1说明分类效果越好。

# 7、注意事项

对于自变量的取值要求、样本含量的计算、变量的选择等方面与二分类一致
有序逻辑回归对于模要求满足平行性假设检验。若平行性假设不成立，就用其他不需要进行平行性假设的模型，或用无序多分类Logistic回归。

# 8、模型理论

# 1.简介

回归是研究被解释变量 Y 对解释变量 X 的依赖关系，即用解释变量的已知值去估计被解释变量的均值。当因变量 Y 为二分类定性的情况时，可以使用二元逻辑回归。然而，在研究中，难免会碰到类似反对、中立、赞成等递进关系的变量，由于其结局不再是两个类，研究其他因素与这种有序因变量的关系时，可以使用有序逻辑回归。

# 2.有序因变量的赋值方法

人们关注的许多社会现象有使用有序分类变量加以测量。例如，医学治疗中（不愈、有效、痊愈）。有序变量假定用数值型取值来代表某一特定属性的次序，然而这些排序不一定反映某一实质尺度上的实际大小。因此，在研究相应的logit模型时，科学的对有序分类变量赋值，具有重要的意义。通常有如下赋值方法：

# (1) 整数赋值

整数赋值是最简单，也是最流行的方法，通过指定一些整数来体现分类数据的次序。例如，坚决反对=1，反对=2，中立=3，赞成=4，坚决赞成=5。整数赋值背后隐含的假设为：相邻类别之间的距离完全相等。

# (2) 中点赋值

有序变量有时从概念上属于连续型变量的分类预测，例如，根据年龄分为：儿童时期（0-18），青壮年（18-48），中年（48-60），老年（60以上）。上例次序变量属于年龄连续变量的离散化形式，若简单的采用整数赋值法，会损失一些有用信息，此时可计算每个区间的中点，并以此作为赋值依据。该赋值法可能存在最后一类开口，需要设置合理的上限；另外某一区间内高度偏态时，中点值的代表性不够好。

# (3) 标准正态分布得分变换

该方法假设分类变量渐进的服从正态分布，对于有序分类变量也做出正态分布假设，则类别赋值的变换方法步骤如下：

计算每类在样本中所占比例
将类别之间的比例累积起来
对每一个类别，找出与其中点（类别中的50%分位数）相对应的累积比例
基于标准正态分布，将中点的累积比例转换成 Z 值
用 Z 值对有序分类变量赋值

# (4) 利用辅助信息的尺度化

前面提及的赋值方法都是在同一次序变量中进行的，实践中更好地方式是利用辅助信息，这些信息要么来自同一数据集中的不同变量或来自其他数据。例如，社会经济地位的次序变量进行赋值，可以借助其中的收入变量进行赋值，也可以借助国际经济社会地位指数。

# 3.有序累积logit模型原理

# (1) 累积概率logit

当响应类别有序时，logit可以利用这个类别顺序，这样得到的模型更有解释性且有更好效果。Y的累积概率是指 Y 落在或低于一个特定点的概率。对于类别 j，第j类的概率为 $π_{j}$ ，累积概率为：

P (Y <= j) = π_{1} + . . . + π_{j}, j = 1, . . ., J

累积概率满足

P (Y <= 1) <= P (Y <= 2) <= . . . <= P (Y <= J) = 1

，累积概率的模型并不利用最后一个概率P(Y<=J)，因为它必然=1。
第 j 个累积logit的模型看作一个二分logit回归模型，分类目标为

{1, . . ., j} 和 {j + 1, . . ., k}

。累积概率的logit为：

l o g i t [P (Y <= j)] = l n (\frac{P (Y <= j)}{1 - P (Y <= j)}) = l n (\frac{π_{1} + . . . + π_{j}}{π_{j + 1} + . . . + π_{j}}), j = 1, . . ., J - 1

例如，J=3时，logit模型为：

l o g i t [P (Y <= 1)] = l n (\frac{π_{1}}{π_{2} + π_{3}}), l o g i t [P (Y <= 2)] = l n (\frac{π_{1} + π_{2}}{π_{3}})

加入解释变量 x 后，有序累积logit模型为：

l o g i t [P (Y <= j)] = l n (\frac{π_{1} + . . . + π_{j}}{π_{j + 1} + . . . + π_{j}}) = α_{j} + β_{1 * x_{1}} + β_{2 * x_{2}} + . . . + β_{k * x_{k}} + ε

模型中的截距项

α_{j}

，是与 j 有关的项。模型中的参数

β

没有下标 j，描述了 x 对应响应变量落在小于或等于 j 的类别相对于大于 j 的类别的对数比率（In odds）效应

# (2) 有序logit模型的假设条件

拆分后各个二分类logit回归的斜率系数相等，仅常数项（截距项）不同，该假设被称为平行线假设或比例假设。例如J=3时， $l o g i t [P (Y <= j)] = α_{j} + β_{1 * x_{1}} + β_{2 * x_{2}}$ ，如下图：

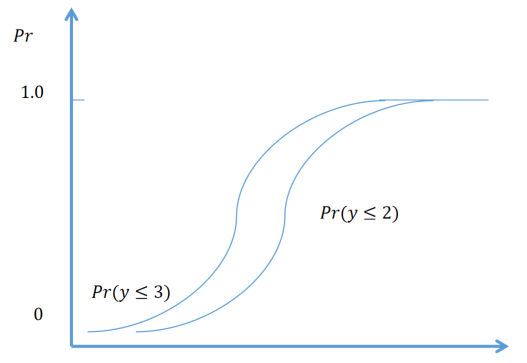
每个 j 的共同效应 $β$ 决定了这两条曲线有相同的形状，任意一条曲线等同于其余任意一条曲线的右或左平移。因此，在使用有序累积logit模型时，首先要做平行线假设检验，若不满足，可尝试更换连接函数，或使用无序多分类logit回归模型拟合，再根据系数估计值考虑处理。

# (3) 预测概率

累积概率的模型表达式为 $P (Y <= j) = \frac{e x p (α_{j} + β x)}{1 + e x p (α_{j} + β x)}$ 。

类别1的概率为： $π_{1} = P (Y <= 1)$ ；
类别2的概率为： $π_{2} = P (Y <= 2) - P (Y <= 1)$ ；
类别3的概率为： $π_{3} = P (Y <= 3) - P (Y <= 2)$ ，以此类推。

以上介绍的是有序累积Logit模型，除此之外，常见的有序Logistic回归还有比例优势模型、连续比值Logit模型和相邻比值Logit模型。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 孙振球，徐勇勇.《医学统计学第4版》.人民卫生出版社.
[3] 侯文, 顾长伟. 累积比数Logistic回归模型及其应用[J]. 辽宁师范大学学报：自然科学版, 2009(4):4.

建议反馈