分层回归

操作视频

# 1、作用

分层回归（层次回归）本质上是建立在回归分析基础上，区别在于分层回归可分为多层，用于研究两个或者多个回归模型之间的差异。分层回归将核心研究的变量放在最后一步进入模型，以考察在排除了其他变量的贡献的情况下，该变量对回归方程的贡献，如果变量仍然有明显的贡献，那么就可以做出该变量确实具有其他变量所不能替代的独特作用的结论。这种方法主要用于，当自变量之间有较高的相关，其中一个自变量的独特贡献难以确定的情况。例如，在研究学习疲倦感中，将性别、年龄、学历等（控制变量）放置在第一层，第二层放置工作压力（核心研究变量）。常用于中介作用或者调节作用研究。

# 2、输入输出描述

输入：多层次的线性回归数据
输出：上一个层次与下一个层次的拟合变化情况，用于分析多加入的变量对自变量（Y）的影响程度。

# 3、案例示例

案例：某高校随机抽取 400 多名大学生，调查其身高、体重、运动时长和肺呼量（Y）数据，控制身高、体重，分析运动时长对肺呼量的影响程度。

# 4、案例数据

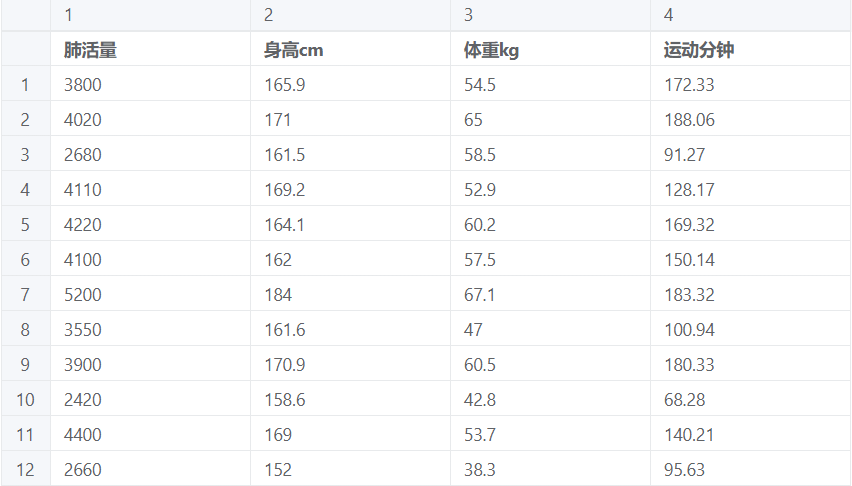
分层回归案例数据

# 5、案例操作

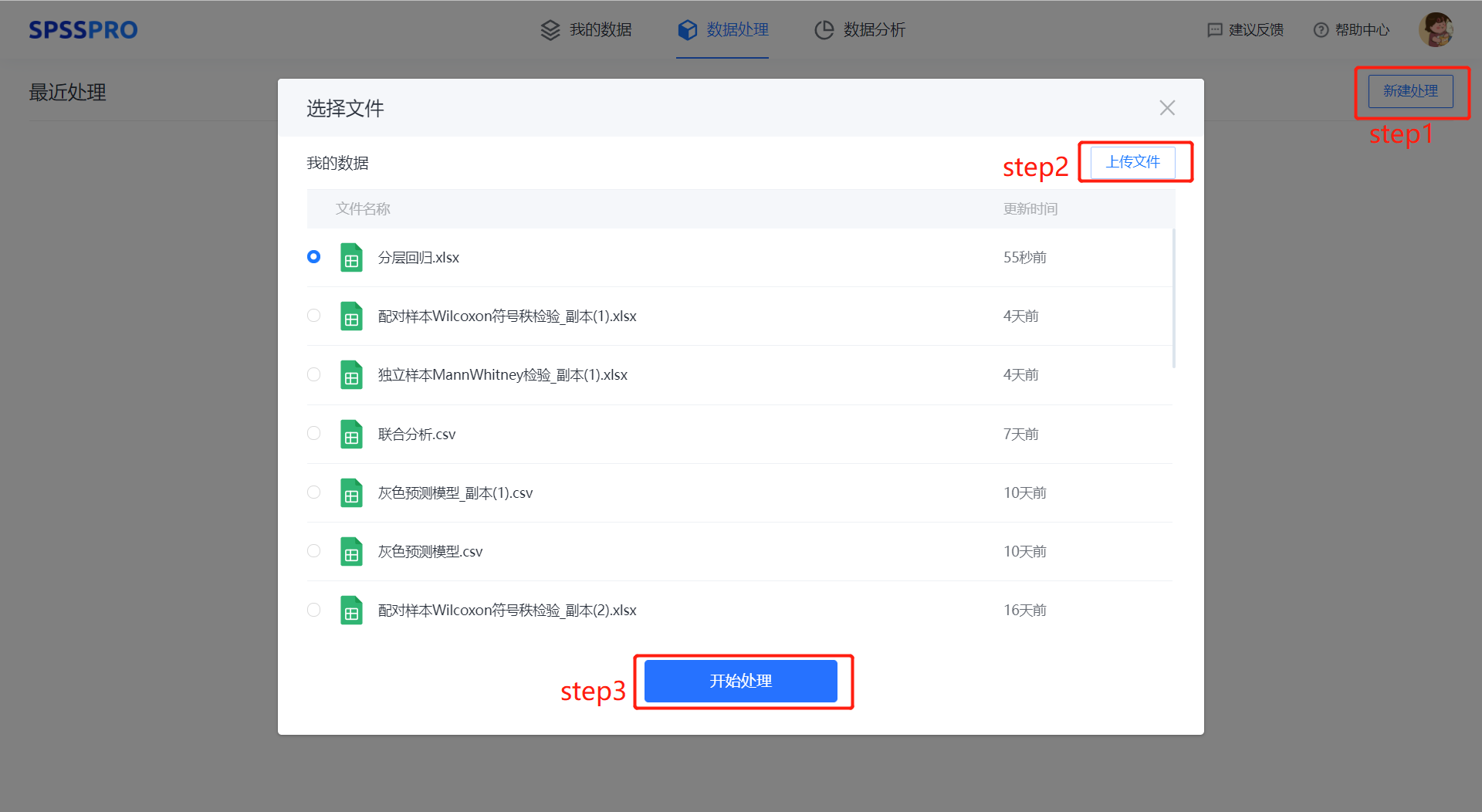
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；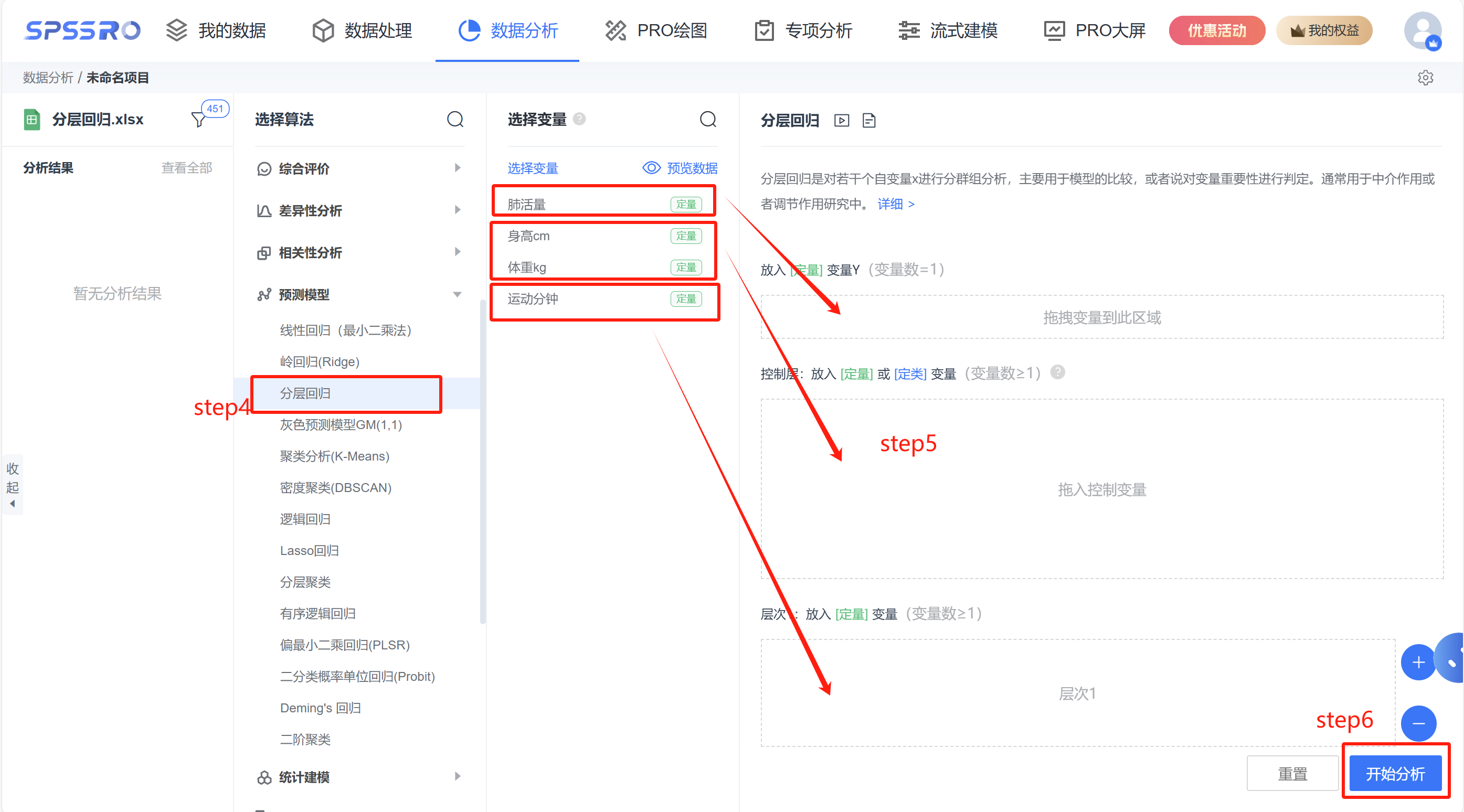

step4：选择【分层回归】；
step5：查看对应的数据数据格式，【分层回归】要求输入定量变量 Y，控制层为定量或定类变量，各层次也为定量或定类变量；
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：分层回归一致性检验

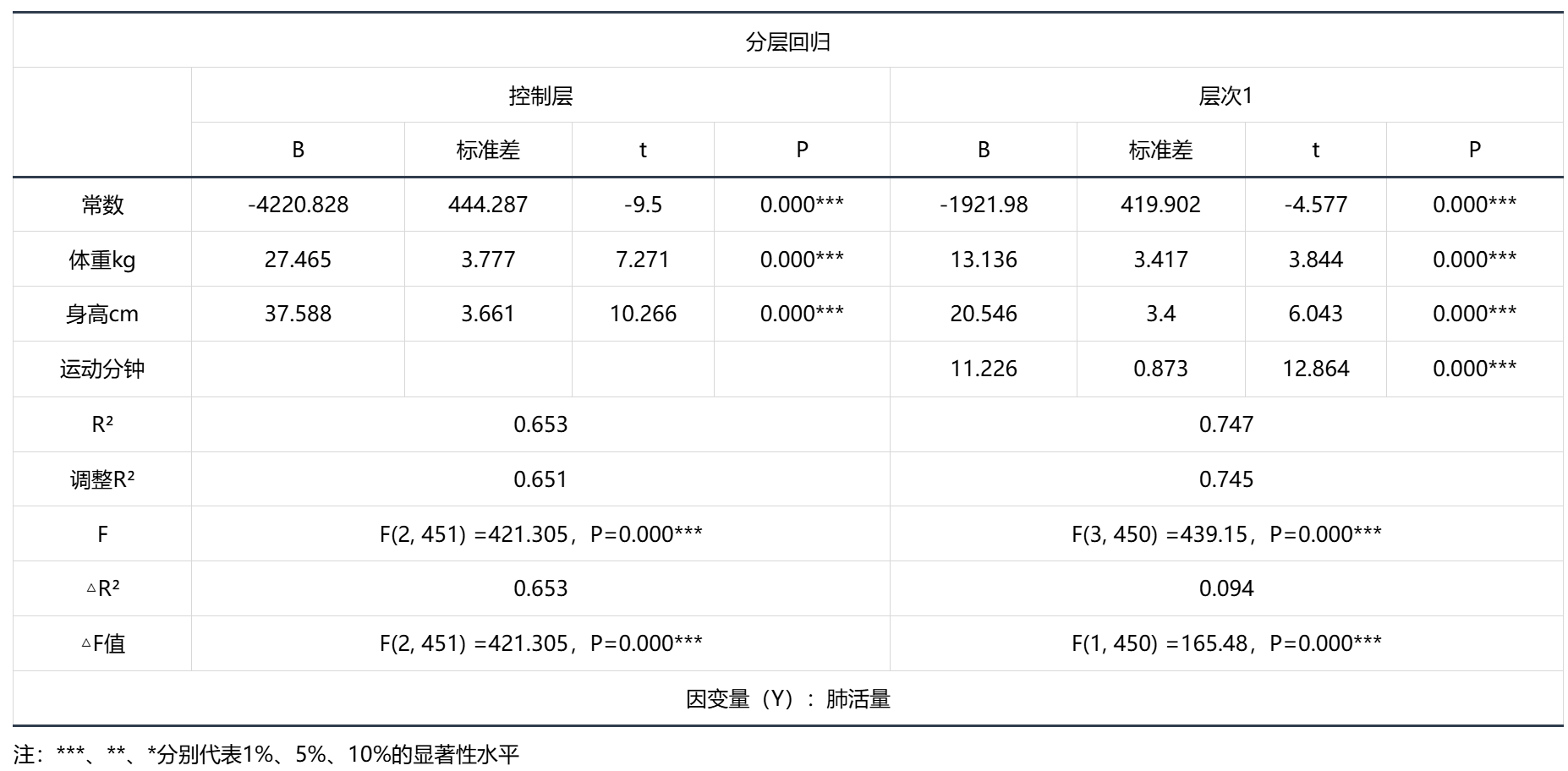
图表说明：

基于分层模型：控制层，包括字段常数、体重 kg、身高 cm,显著性 P 值为 1.000,水平上呈现显著性，拒绝原假设，因此模型有效，同时模型的拟合优度 R² 为 0.653，模型表现较为良好，因此模型满足基本满足要求。
基于分层模型：分层 1，包括字段常数、体重 kg、身高 cm、运动分钟,显著性 P 值为 1.000,水平上呈现显著性，拒绝原假设，因此模型有效，同时模型的拟合优度 R² 为 0.747，模型表现较为良好，因此模型满足基本满足要求。
总结：以上两个模型都是有效的，并且控制层到分层 1 的 R² 增加了 0.094，即说明运动时长（分钟）会对肺活量产生了 9.4%的解释力度。

# 7、注意事项

控制层是相对于分层模型 1 的，当分层模型有多个时，spsspro 的分层模型所对应的控制层是前一个分层模型。即分层模型 2 的控制层是分层模型 1，分层模型 3 的控制层是分层模型 2。

# 8、模型理论

分层回归其实是对两个或多个回归模型进行比较。我们可以根据两个模型所解释的变异量的差异来比较所建立的两个模型。一个模型解释了越多的变异，则它对数据的拟合就越好。通常用于中介作用或者调节作用研究中。

# 9、参考文献

[1]Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]聂洪涛,韩欣悦. 我国有效专利区域发展"马太效应"困境及其调适——基于分层回归的实证研究[J]. 经济论坛,2021(8). DOI:10.3969/j.issn.1003-3580.2021.08.011.

建议反馈