灰色预测模型GM(1,1)

操作视频

# 1、作用

灰色预测是一种针对含有不确定因素、不完全信息或少量数据样本的系统进行预测的有效方法。它通过鉴别系统内部各因素之间发展趋势的相似性和差异性（即进行灰色关联分析），并对原始数据进行累加生成（AGO, Accumulated Generating Operation）等处理，以弱化数据的随机性，增强数据的规律性。随后，基于处理后的数据序列建立一阶单变量微分方程模型（即GM(1,1)模型），从而实现对事物未来发展趋势的预测。

# 2、输入输出描述

输入：1个时间序列数据定量变量：通常是一组按时间顺序排列的观测值，代表某一现象或指标在不同时间点的表现。
输出：灰色预测的拟合预测结果：包括模型对历史数据的拟合值（即回代检验）和未来几个时间点的预测值。这些结果通常以数值形式给出，并可能伴随有预测误差、置信区间等统计信息。

# 3、案例示例

案例：基于某杂志 2006-2021 年某产品的年销售量，使用灰色预测模型对未来三年销售量进行预测。

# 4、案例数据

灰色预测模型案例数据

# 5、案例操作

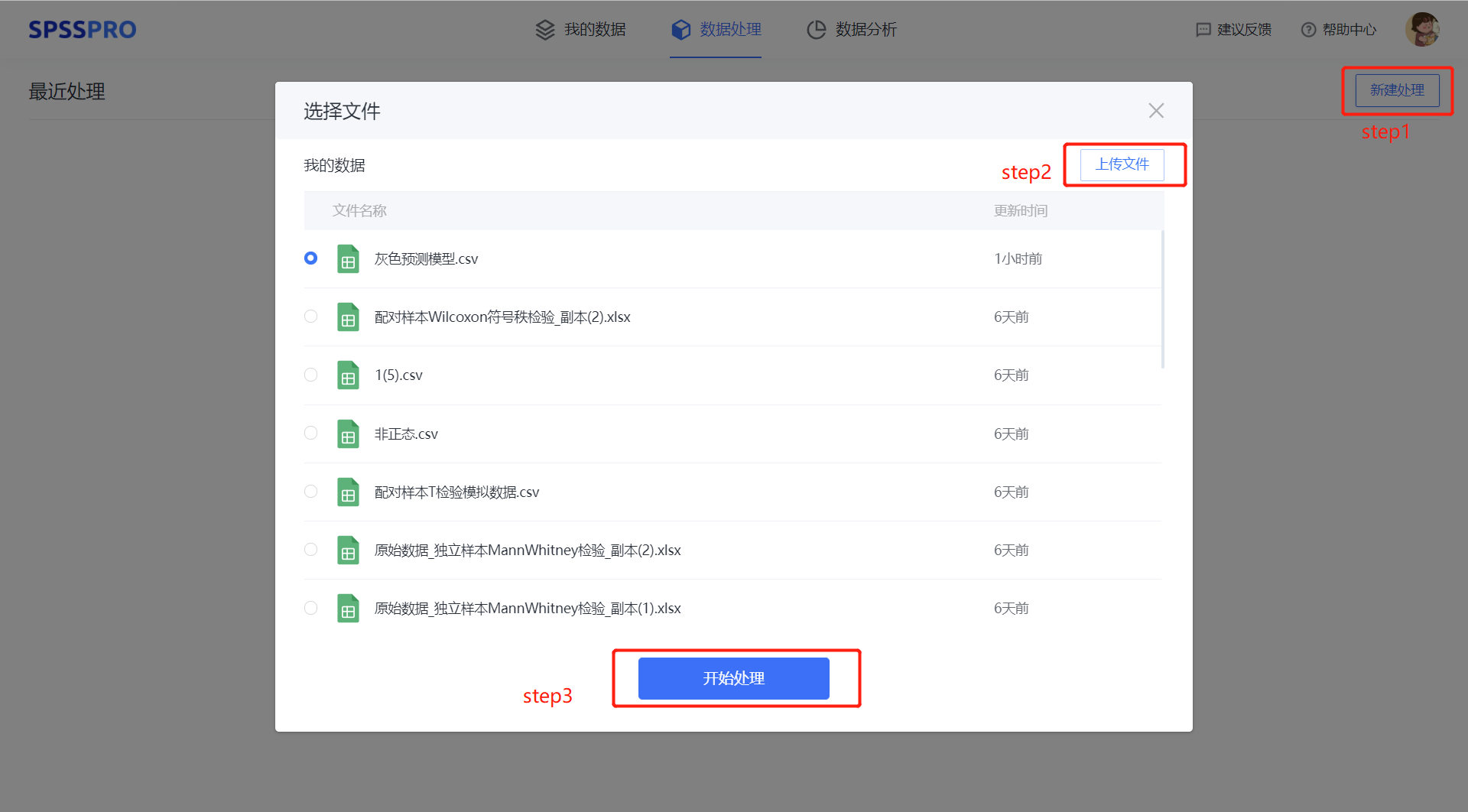
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

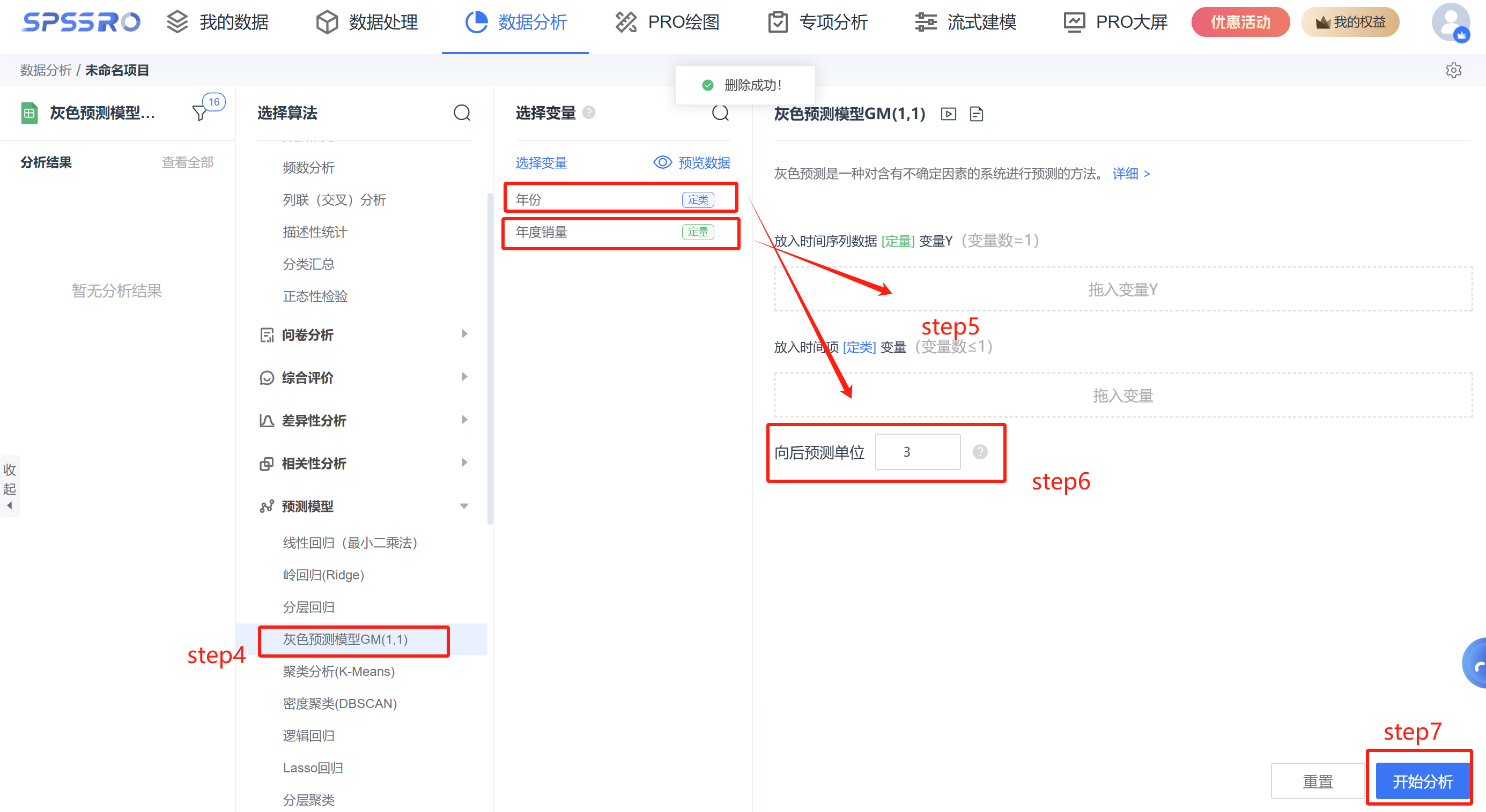
step4：选择【灰色预测模型】；
step5：查看对应的数据数据格式，【灰色预测模型】要求输入１个时间序列数据定量变量。
step6：选择向后预测的期数。
step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：级比检验结果表

索引项	原始值	级比值	平移转换后序列值	平移转换后级比值
2006	153.1	-	433.1	-
2007	159.2	0.962	439.2	0.986
2008	162.3	0.981	442.3	0.993
2009	159.1	1.02	439.1	1.007
2010	155.1	1.026	435.1	1.009
2011	161.2	0.962	441.2	0.986
2012	171.5	0.94	451.5	0.977
2013	168.4	1.018	448.4	1.007
2014	180.4	0.933	460.4	0.974
2015	201.6	0.895	481.6	0.956
2016	218.7	0.922	498.7	0.966
2017	247	0.885	527	0.946
2018	253.7	0.974	533.7	0.987
2019	261.4	0.971	541.4	0.986
2020	273.2	0.957	553.2	0.979
2021	279.4	0.978	559.4	0.989

图表说明：上表格展示了序列值和级比值。若所有的级比值都位于区间（e^(-2/(n+1)), e^(2/n+1)）内，说明数据适合模型构建。若不通过级比检验，则对序列进行“平移转换”，从而使得平移转换后序列满足级比检验。由上表可知，原序列至少有一个级比值不位于区间（0.889, 1.125）内，此时应对原序列进行平移转换，目的是通过给序列中的每个数据点加上一个常数 c 来调整级比值，spsspro 自动搜索到 c=9，令原序列都加上 9 构成平移转换后的序列，平移转换后的序列的级比值都位于位于区间（0.889, 1.125），因此平移转换后的序列适合构建灰色预测模型。

输出结果 2：灰色模型构建 

发展系数 a	灰色作用量 b	后验差比 C 值
-0.021	401.899	0.08

图表说明  ：上表格展示了发展系数、灰色作用量、后验差比值。由发展系数和灰色作用量可以构建灰色预测模型。
● 发展系数表示数列的发展规律和趋势，灰色作用量反映数列的变化关系；
● 后验差比值可以验证灰色预测的精度，后验差比值越小，则说明灰色预测精度越高；
● 一般后验差比值 C 值小于 0.35 则模型精度高，C 值小于 0.5 说明模型精度合格，C 值小于 0.65 说明模型精度基本合格，如果 C 值大于 0.65，则说明模型精度不合格。从上表分析可以得到，后验差比值为 0.08，说明建立的灰色预测模型精度高。

输出结果 3：二阶差分图

索引项	原始值	预测值	残差	相对误差（%）
2006	153.1	153.1	0	0
2007	159.2	135.383	23.817	14.961
2008	162.3	144.226	18.074	11.136
2009	159.1	153.257	5.843	3.672
2010	155.1	162.481	-7.381	4.759
2011	161.2	171.901	-10.701	6.638
2012	171.5	181.521	-10.021	5.843
2013	168.4	191.347	-22.947	13.626
2014	180.4	201.381	-20.981	11.63
2015	201.6	211.629	-10.029	4.975
2016	218.7	222.096	-3.396	1.553
2017	247	232.785	14.215	5.755
2018	253.7	243.702	9.998	3.941
2019	261.4	254.851	6.549	2.505
2020	273.2	266.237	6.963	2.549
2021	279.4	277.866	1.534	0.549

图表说明：上表展示了灰色预测模型的拟合结果表。相对误差值越小越好，一般情况下小于 20%即说明拟合良好。总的来说，模型平均相对误差为 5.881%，意味着模型拟合效果良好。

输出结果 4：模型拟合预测图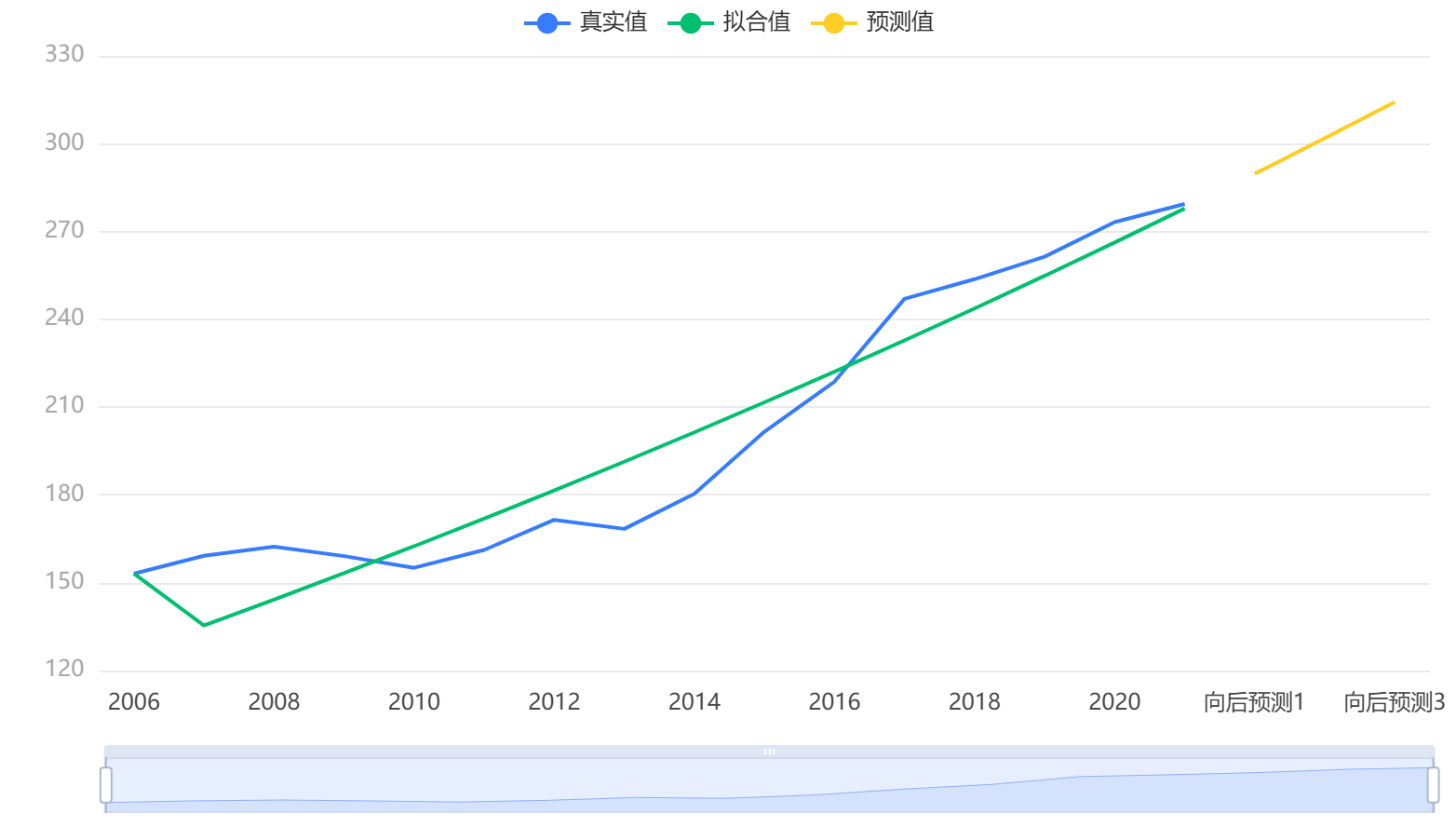
图表说明：上图展示了灰色预测模型的拟合预测图。

输出结果 5：模型预测结果表 

预测阶数	预测值
1	289.743
2	301.872
3	314.260

图表说明：上表展示了灰色预测模型的预测结果表。

# 7、注意事项

灰色预测模型适用于少量数据时使用(比如 20 个以内)，大量数据时不适合。
GM(1,1)模型仅适用于中短期预测，不建议进行长期预测。

# 8、模型理论

GM(1,1)预测模型的简要原理是指:首先利用累加的技术使数据具备指数规律，然后建立一阶微分方程并对其求解，将所求结果再累减还原，即为灰色预测值，从而对未来进行预测。
步骤 1：在建立灰色预测模型之前必须要保障建模方法的可行性，即需要对已知的原始数据进行级比检验。设初始非负数据序列为

只有当所有的 σ(k) 全部落入计算范围内才可以进行模型的建立。级比的计算和判断公式分别为:

通过累加运算后得到

的一阶累加序列可以弱化

的扰动：

是

的紧邻均值生成的序列

故可以求得 GM(1,1)模型对应微分方程为:

其中

为GM(1,1) 模型的背景值。

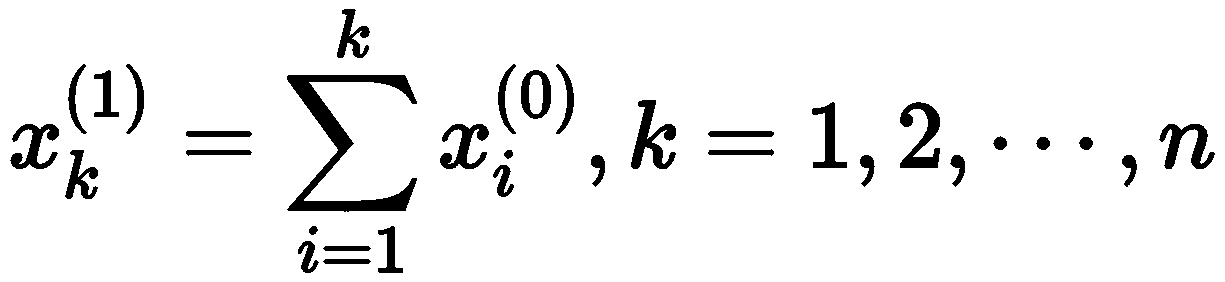
步骤 2：构建数据矩阵 B 及数据向量 Y ，分别为

则灰色微分方程的最小二乘估计参数列满足

其中， a 主要控制系统发展态势,被称为发展系数; b 的大小反映数据变化的关系,被称为灰色作用量。

步骤 3：建立模型并求解生成值与还原值。依据公式求解, 可得到预测模型

经过累减,得到还原预测值。

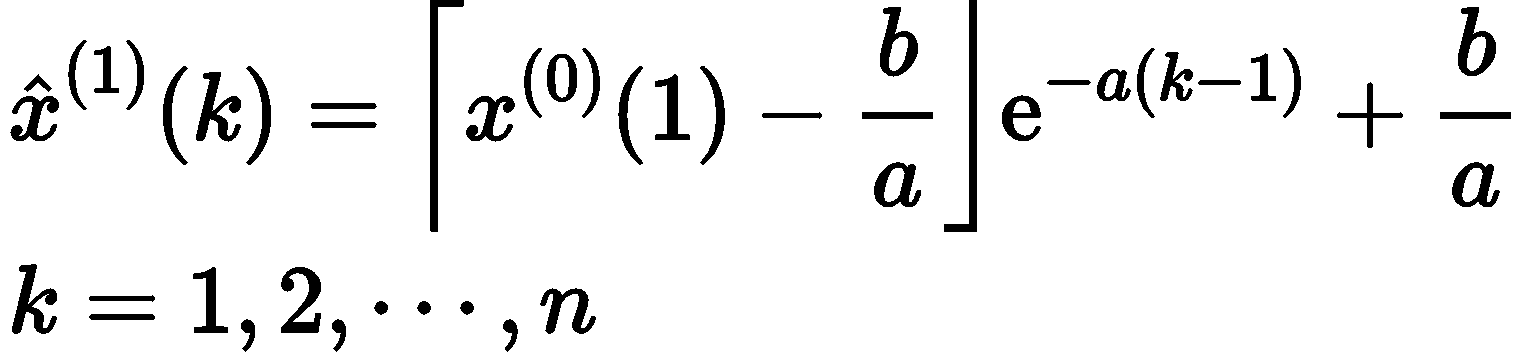
# 9、参考文献

Step 1:数据准备（平移转换）
平移常数 $C = 280$ ，平移后序列 $X^{(0)}$ ：

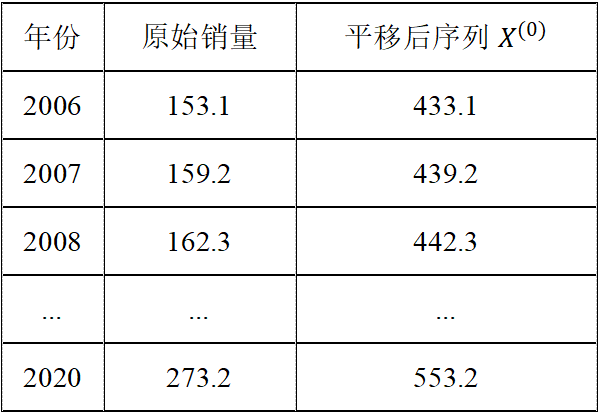
Step 2:级比检验
级比公式：

$σ (k) = \frac{X^{(0)} (k - 1)}{X^{(0)} (k)}, 区间要求： (e^{- \frac{2}{n + 1}}, e^{\frac{2}{n + 1}})$

示例计算:

2007年： $σ (2007) = \frac{433.1}{439.2} \approx 0.986$
2008年： $σ (2008) = \frac{439.2}{442.3} \approx 0.993$
2009年： $σ (2009) = \frac{442.3}{439.1} \approx 1.007$
...（其余年份计算过程类似）

全部级比值:

$σ = [0.986, 0.993, 1.007, 1.009, 0.986, 0.977, 1.007, 0.974, 0.956, 0.966, 0.946, 0.987, 0.986, 0.979]$

计算得

n = 15

，区间为

(0.889, 1.125)

。

Step 3:累加序列生成
一阶累加序列 $X^{(1)}$ ：

$X^{(1)} (k) = \sum_{i = 1}^{k} X^{(0)} (i)$

计算示例：

$X^{(1)} (2006) = 433.1$
$X^{(1)} (2007) = 433.1 + 439.2 = 872.3$
$X^{(1)} (2008) = 872.3 + 442.3 = 1314.6$
依此类推，最终累加序列为：

$X^{(1)} = [433.1, 872.3, 1314.6, 1756.9, 2192.0, 2633.2, 3084.7, 3533.1, 3993.5, 4475.1, 4973.8, 5500.8, 6034.5, 6575.9, 7129.1]$

Step 4:紧邻均值序列 $Z^{(1)}$
公式：

$Z^{(1)} (k) = 0.5 \times (X^{(1)} (k) + X^{(1)} (k - 1))$

计算示例：

$Z^{(1)} (2007) = 0.5 \times (433.1 + 872.3) = 652.7$
$Z^{(1)} (2008) = 0.5 \times (872.3 + 1314.6) = 1093.45$
依此类推，得到 $Z^{(1)}$ 序列（共14个值）。

Step 5:构建矩阵 $B$ 和向量 $Y$
矩阵 $B$ 和向量 $Y$ 结构如下：

$B = [\begin{matrix} - 652.7 & 1 \\ - 1093.45 & 1 \\ ⋮ & ⋮ \\ - 7129.1 & 1 \end{matrix}]$ , $Y = [\begin{matrix} 439.2 \\ 442.3 \\ ⋮ \\ 553.2 \end{matrix}]$

以此类推计算

Step 6:最小二乘估计参数 $a$ 和 $b$
公式：

$u = [\begin{matrix} a \\ b \end{matrix}] = (B^{T} B)^{- 1} B^{T} Y$

代入数据计算得：

$a = - 0.021, b = 401.899$

Step 7:预测模型建立
白化方程解：

${\hat{X}}^{(1)} (k) = (X^{(0)} (1) - \frac{b}{a}) e^{- a (k - 1)} + \frac{b}{a}$

代入

a = - 0.021

b = 401.899

X^{(0)} (1) = 433.1

，得：

${\hat{X}}^{(1)} (k) = (433.1 - \frac{401.899}{- 0.021}) e^{0.021 (k - 1)} + \frac{401.899}{- 0.021}$

化简后为：

${\hat{X}}^{(1)} (k) = 19470.9 e^{0.021 (k - 1)} - 19037.8$

Step 8:还原预测值
累减还原公式：

${\hat{X}}^{(0)} (k) = {\hat{X}}^{(1)} (k) - {\hat{X}}^{(1)} (k - 1)$

计算示例（2021年预测，对应

k = 16

）：

${\hat{X}}^{(1)} (16) = 19470.9 e^{0.021 \times 15} - 19037.8 \approx 837.3$

${\hat{X}}^{(0)} (16) = 837.3 - 7129.1$

Step 9:模型检验

后验差比 $C = 0.08$ ：精度高（<0.35）
平均相对误差 5.881%：拟合效果良好。 -未来3期预测值（已还原）：

$2021 : 289.743, 2022 : 301.872, 2023 : 314.260$

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 邓聚龙. 灰色预测与灰决策[M]. 武汉:华中科技大学出版社,2002.

建议反馈