分层聚类
# 1、作用
聚类就是按照某个特定标准把一个数据集分割成不同的类或簇。分层聚类法作为聚类的一种,是对给定数据对象的集合进行层次分解,根据分层分解采用的分解策略。就划分策略可以分为聚合的(agglomerative)和分裂的(divisive)分层聚类,聚合法最初将每个数据点作为一个单独的聚类,然后迭代合并,直到最后的聚类中包含所有的数据点。它也被称为自下而上的方法。分裂聚类遵循自上而下的流程,从一个拥有所有数据点的单一聚类开始,迭代地将该聚类分割成更小的聚类,直到每个聚类包含一个数据点。目前系统暂时只支持凝聚的分层聚类。
# 2、输入输出描述
输入:一个以上的定量变量和可选的索引项。
输出:个体或者变量被划分的类别和树状图(谱系图)。
# 3、案例示例
根据各区域家庭日常开支,包括食品、衣食、燃料、住房、生活用品及其他、文化生活服务支出。用分层聚类分析方法将全国 16 个省市(区域)的生活支出状况进行归类分析,得出这些区域居民消费支出情况的分类情况。
# 4、案例数据
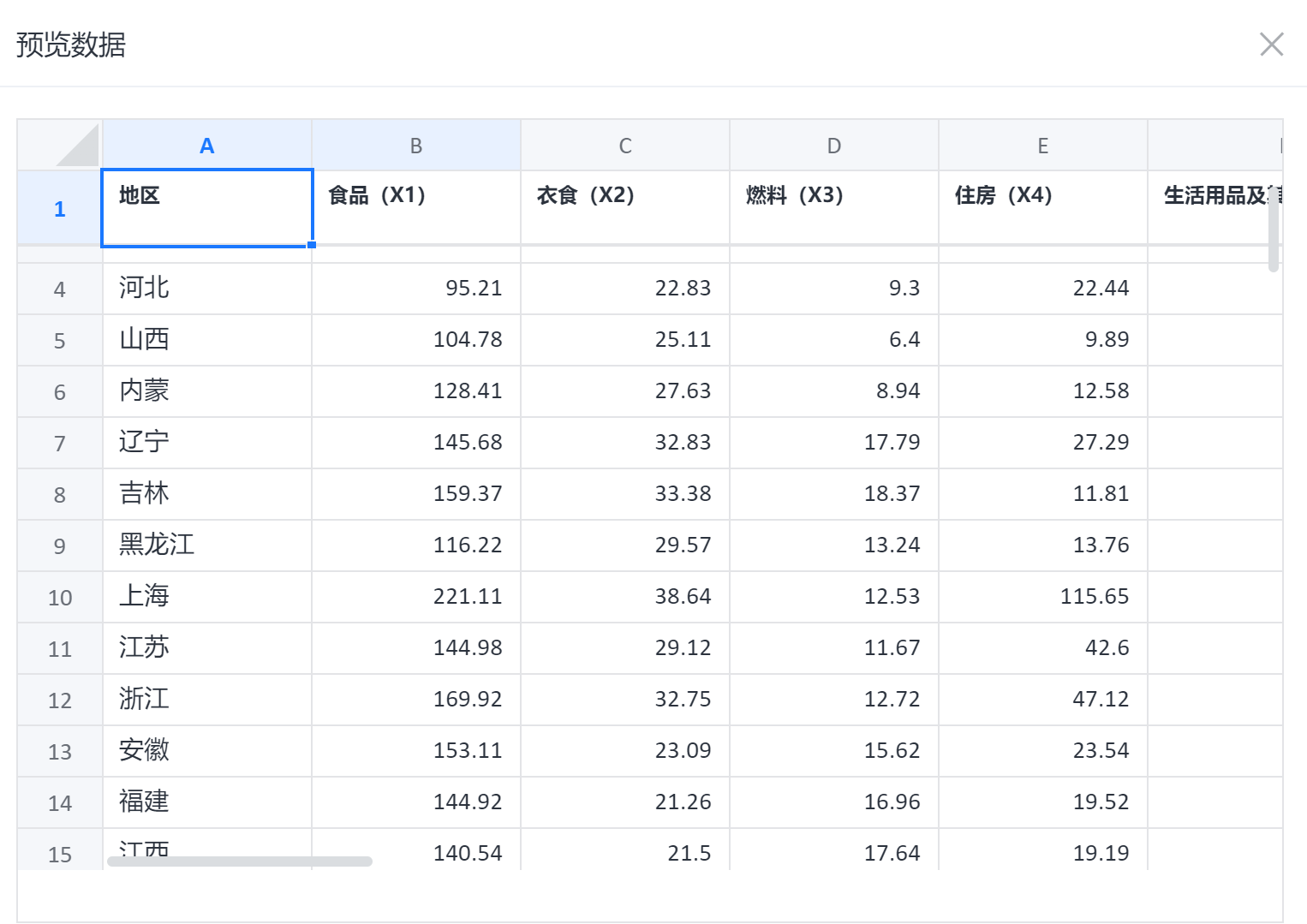
分层聚类案例数据
# 5、案例操作
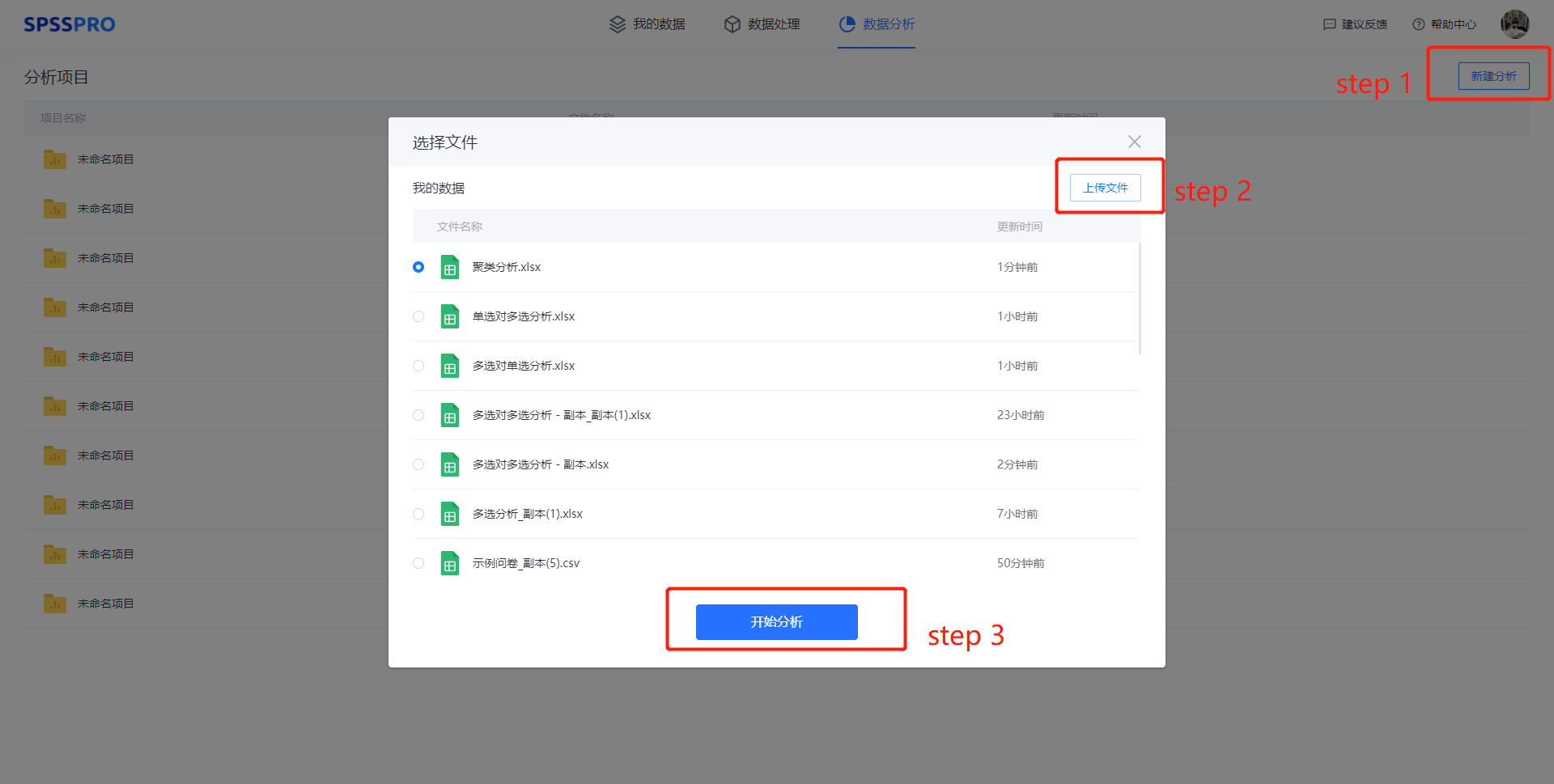
Step1:新建分析;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;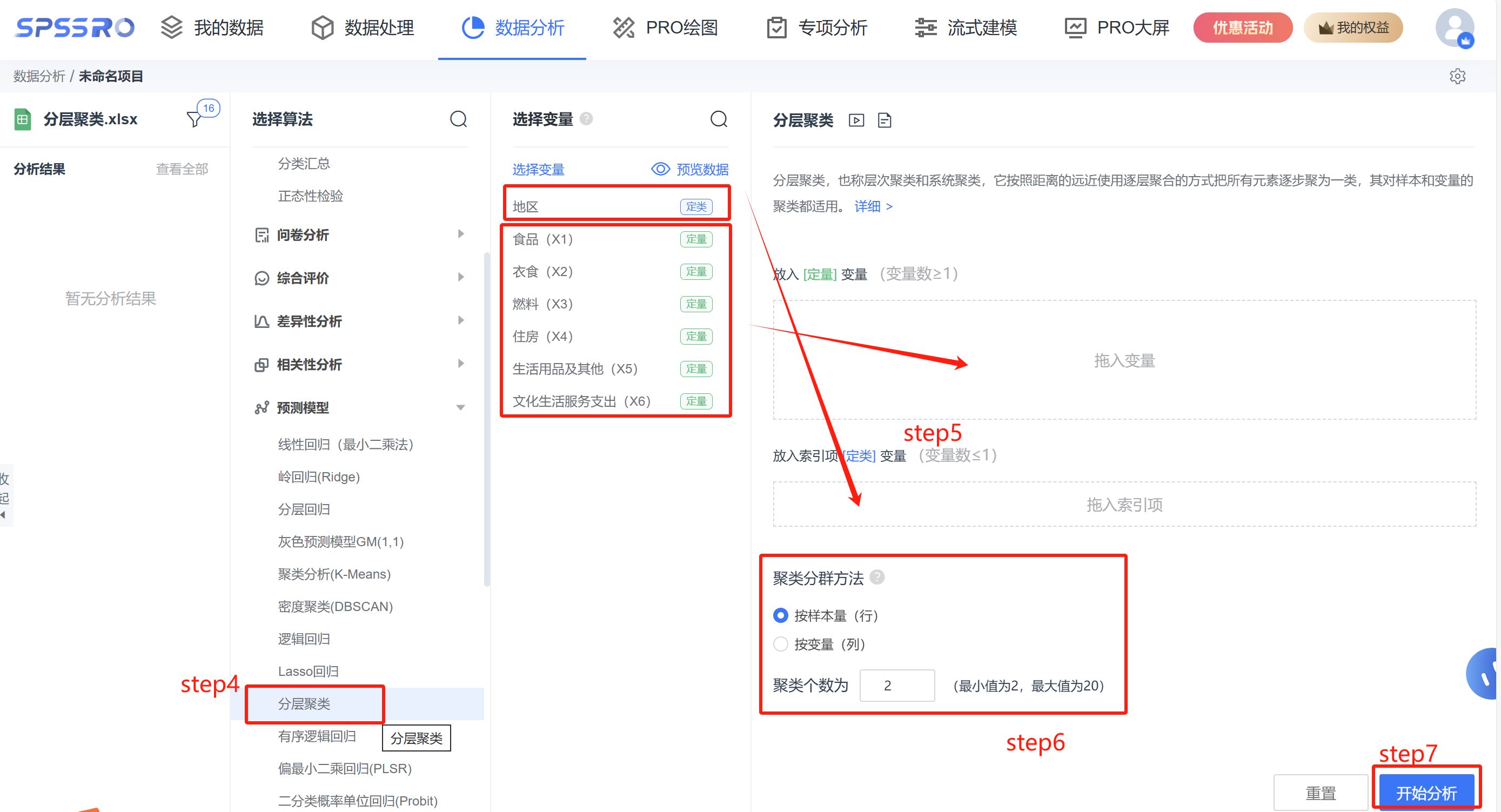
step4:选择【分层聚类】;
step5:查看对应的数据数据格式,按要求放入【分层聚类】的变量;
step6:选择聚类分群方法和聚类个数;
step7:点击【开始分析】,完成全部操作。
# 6、输出结果分析
输出结果 1:数据情况汇总
| 案例 | |||||
|---|---|---|---|---|---|
| 有效 | 缺失 | 总计 | |||
| N | 百分比(%) | N | 百分比(%) | N | 百分比(%) |
| 16 | 100 | 0 | 0 | 16 | 100 |
图表说明:上表展示了数据的有效和缺失情况,当某行数据存在缺失时,则计入缺失数据。
输出结果 2:聚类表
| 阶 | 群集组合 | 系数 | 元素个数 | 新集群 | |
|---|---|---|---|---|---|
| 集群 1 | 集群 2 | ||||
| 1 | 河北 | 河南 | 6.92 | 2 | 聚类 1 |
| 2 | 福建 | 江西 | 7.512 | 2 | 聚类 2 |
| 3 | 安徽 | 聚类 2 | 11.932 | 3 | 聚类 3 |
| 4 | 内蒙 | 黑龙江 | 13.599 | 2 | 聚类 4 |
| 5 | 山西 | 聚类 1 | 14.343 | 3 | 聚类 5 |
| 6 | 天津 | 江苏 | 15.499 | 2 | 聚类 6 |
| 7 | 辽宁 | 聚类 6 | 21.185 | 3 | 聚类 7 |
| 8 | 吉林 | 聚类 3 | 21.511 | 4 | 聚类 8 |
| 9 | 聚类 4 | 聚类 5 | 24.436 | 5 | 聚类 9 |
| 10 | 山东 | 聚类 9 | 26.729 | 6 | 聚类 10 |
| 11 | 聚类 7 | 聚类 8 | 30.182 | 7 | 聚类 11 |
| 12 | 北京 | 浙江 | 30.956 | 2 | 聚类 12 |
| 13 | 聚类 10 | 聚类 11 | 42.425 | 13 | 聚类 13 |
| 14 | 聚类 12 | 聚类 13 | 65 | 15 | 聚类 14 |
| 15 | 上海 | 聚类 14 | 126.398 | 16 | 聚类 15 |
图表说明:上图是聚类表,在聚类表中列出了逐步聚类的过程。
输出结果 3:聚类散点图
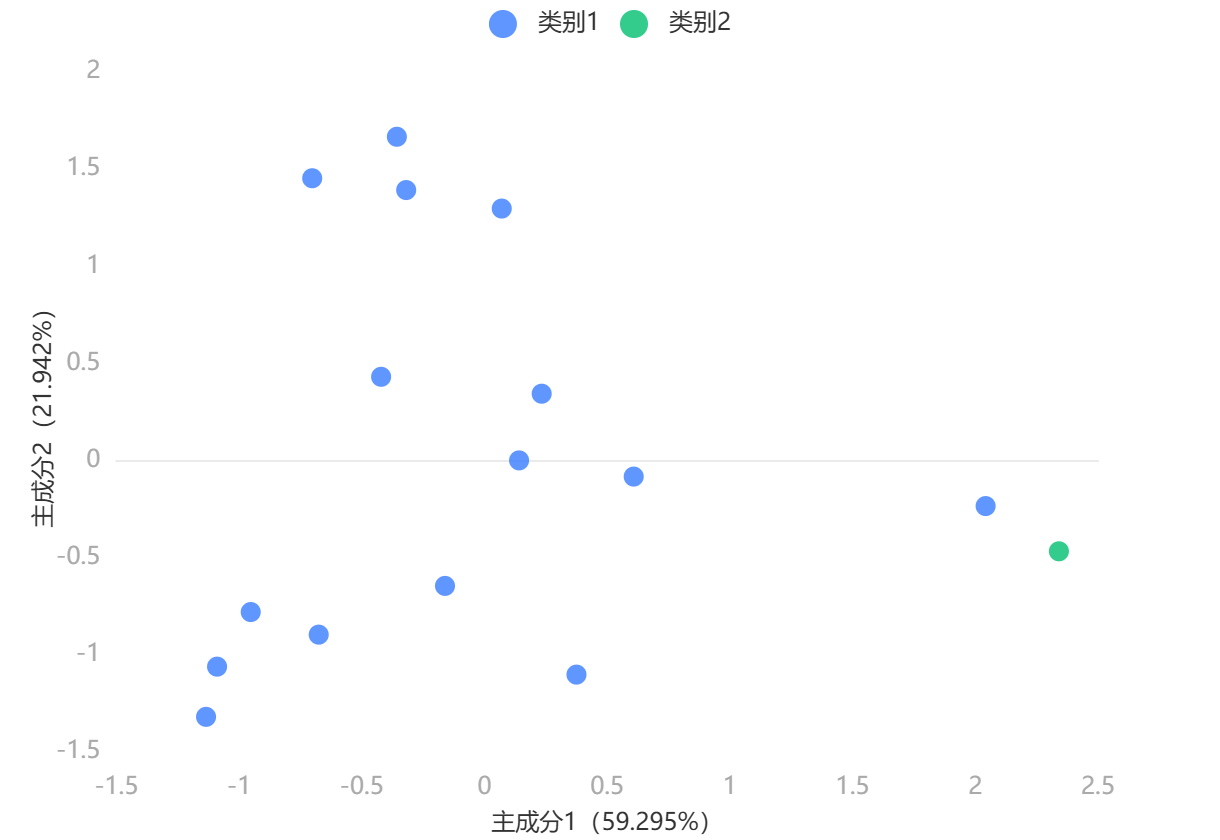
图表说明:若对不同样本量(行)进行聚类分群,此时变量数等于两个,上图是根据两变量的数据绘制出来的散点图;或者此时变量数大于两个,上图是提取主成分分析(PCA)降维后前两个主成分来绘制散点图,在一定程度上可查看聚类效果(若是前两个主成分的方差解释率较低,该图的意义不大)。
输出结果 4:聚类树状图
图表说明:上图以可视化的形式展示了分层聚类的聚类情况,如果聚类的类别超过 50 个,此图将仅能下载查看。
分析:需要结合聚类树与实际情况进行分析,可以通过分界线决定这些数据到底是分成多少类,也可用作分析哪些变量之间较为接近。
输出结果 5:评价指标
图表说明:
● 轮廓系数:对于一个样本集合,它的轮廓系数是所有样本轮廓系数的平均值。轮廓系数的取值范围是[-1,1],同类别样本距离越相近不同类别样本距离越远,分数越高,聚类效果越好。
● DBI(Davies-bouldin):该指标用来衡量任意两个簇的簇内距离之后与簇间距离之比。该指标越小表示聚类效果越好。
● CH(Calinski-Harbasz Score):通过计算类内各点与类中心的距离平方和来度量类内的紧密度(分母),通过计算类间中心点与数据集中心点距离平方和来度量数据集的分离度(分子),CH指标由分离度与紧密度的比值得到,CH越大表示聚类效果越好。
# 7、注意事项
- 如果各变量数据的水平相差很大,分析前要进行标准化处理;
- 分层聚类针对定量数据进行分析;
- 分层聚类合适的类别数,需要结合聚类树状图和实际情况进行分析;
- 分层聚类更适合小样本聚类。
# 8、模型理论
1.简介 层次聚类是在不同的“层次”上对样本数据集进行划分,一层一层地进行聚类。就划分策略可分为自底向上的凝聚方法和自上向下的分裂方法。
2.原理
层次聚类可以由上向下把大的类别(cluster)分割,叫作分裂法,比如 DIANA;也可以由下向上对小的类别进行聚合,叫作凝聚法,比如 AGNES;一般用的比较多的是由下向上的凝聚方法。
DIANA 先将所有样本当作一整个簇,然后找出簇中距离最远的两个簇进行分裂,不断重复到预期簇或者其他终止条件;AGNES 先将所有样本的每个点都看成一个簇,然后找出距离最小的两个簇进行合并,不断重复到预期簇或者其他终止条件。
3.步骤:
1)初始化:把每个样本各自归为一类,计算每两个类之间的距离,也就是样本之间的相似度;
2)寻找各个类之间最近的两个类,把它们归为一类;
3)重新计算新生成的这个类与各个旧类之间的距离(相似度);
4)重复(2)(3)步,直到所有的样本都归为一类,结束。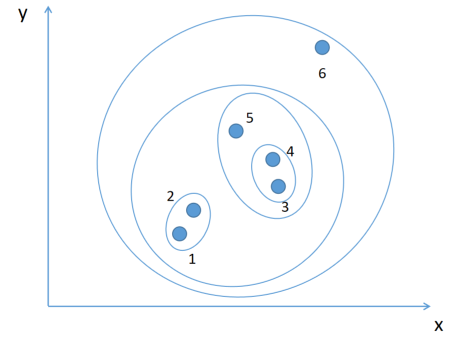
上图为分层聚类过程示意图
相似度计算方法:
关键的步骤为如何判断两个类之间的相似度,常见的有以下几种方法:
1)SingleLinkage:取两个类中最近的两个样本之间的距离作为两个集合的距离,也就是说最近两个样本之间的距离越小,这两个类之间的相似度就越大。
2)Complete Linkage:取两个集合距离最远的两个点的距离作为两个集合的距离。
以上两种相似度定义方法的共同问题是:只考虑了某个特有的数据,而没有考虑数据整体的特点。
3)Average Linkage:把两个集合中的点两两距离全部放在一起求平均值,相应的能得到一点合适的结果。
4)取两两距离的中值,与取平均值相比更加能够解除个别偏离样本对结果的干扰。
5)
求每个集合的中心点(就是将集合中的所有元素的对应维度相加然后再除以元素个数得到的一个向量),然后用中心点代替集合再去就集合间的距离。
4.总结 一般来说,当考虑聚类效率时,我们选择平面聚类,当平面聚类的潜在问题(不够结构化,预定数量的聚类,非确定性)成为关注点时,我们选择层次聚类。另外,层次聚类适合小样本聚类。
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] Jain, A. K. , and R. C. Dubes . "Algorithms for clustering data." Technometrics 32.2(1988):227-229.
