Lasso回归

# 1、作用

Lasso 回归（Least absolute shrinkage and selection operator regression）是一种替代最小二乘法的压缩估计方法。Lasso 的基本思想是建立一个 L1 正则化模型，因此也被称为L1正则化（L1 regularization）,其在模型建立过程中会压缩一些系数和设定一些系数为零，当模型训练完成后，这些权值等于 0 的参数就可以舍去，起到筛选变量的效果，从而使模型更为简单，以避免共线性和过拟合。Lasso回归可以利用较少样本量，高效地筛选较多变量，因此被广泛用于存在多重共线性数据的拟合和变量选择，同时在基因组学、影像学以及其他小样本分析领域中发挥着重要的作用。

# 2、输入输出描述

输入：自变量 X 至少为一项或以上的定量变量或二分类定类变量，因变量 Y 要求为定量变量（若为定类变量，请使用逻辑回归）。
输出：模型检验优度的结果，自变量对因变量的线性关系和变量筛选结果等。

# 3、案例示例

案例：现对一批糖尿病患者进行分析，分别获得了年龄、性别、体重指数、平均⾎压等数据，现使用 Lasso 回归分析⼀年后疾病进展的测量值和重要影响变量。

# 4、案例数据

# 5、案例操作

Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

step4：选择【Lasso 回归】；
step5：查看对应的数据数据格式，【Lasso 回归】要求自变量 X 至少一项或以上的定量变量或二分类定类变量，因变量 Y 要求为定量变量。
step6：选择自动选择 λ 值或者手动输入 λ 值；
step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：Lasso 回归交叉验证图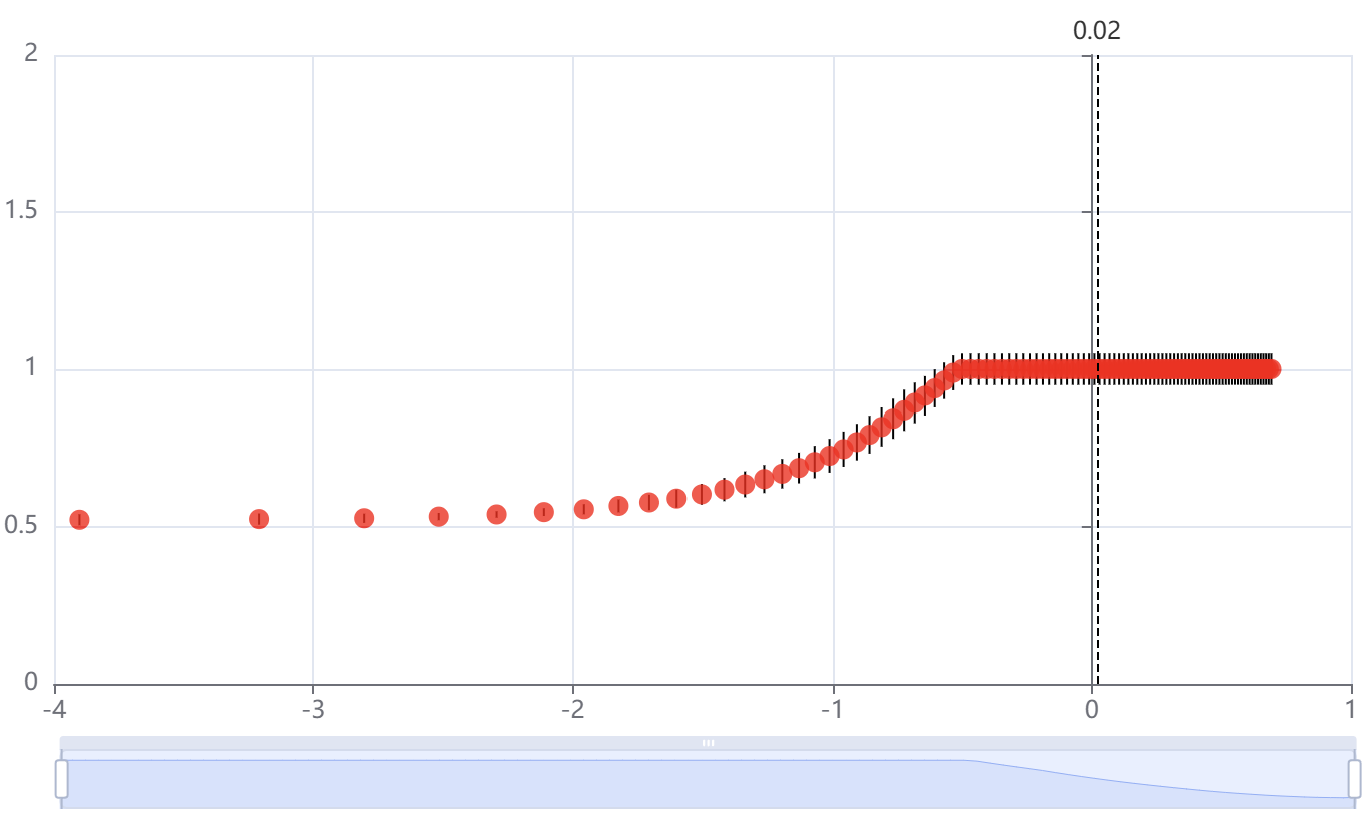

图表说明：上图以可视化形式展示了使用交叉验证选择 λ 值的情况。
纵坐标：模型均方误差
横坐标：λ 的对数值
智能分析：为使得均方误差最小确定 λ=0.02，log(λ)=-3.902。
分析：使用交叉验证的方法进行 λ 值的选择，选择的标准是使得模型均方误差最小，SPSSPRO 自动给出了当均方误差最小的 λ 值，为 0.02。

输出结果 2：λ 与模型回归系数图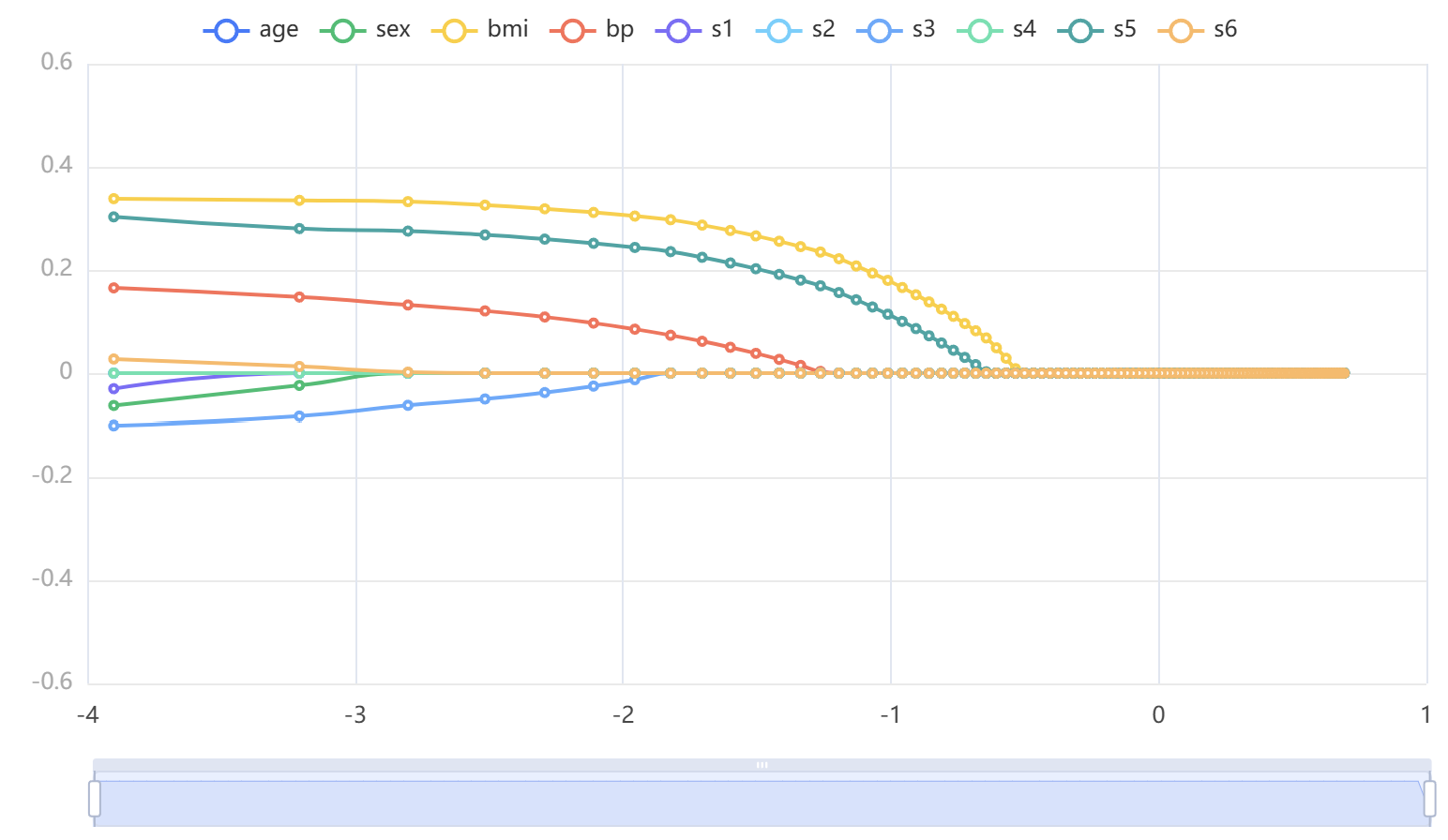

图表说明：上图展示了随着 λ 的对数值变化，模型系数变化的情况。
分析：随着 λ 的对数值变化，模型系数也在变化，变为 0 的时候可以认为被排除出了模型。

输出结果3：模型系数表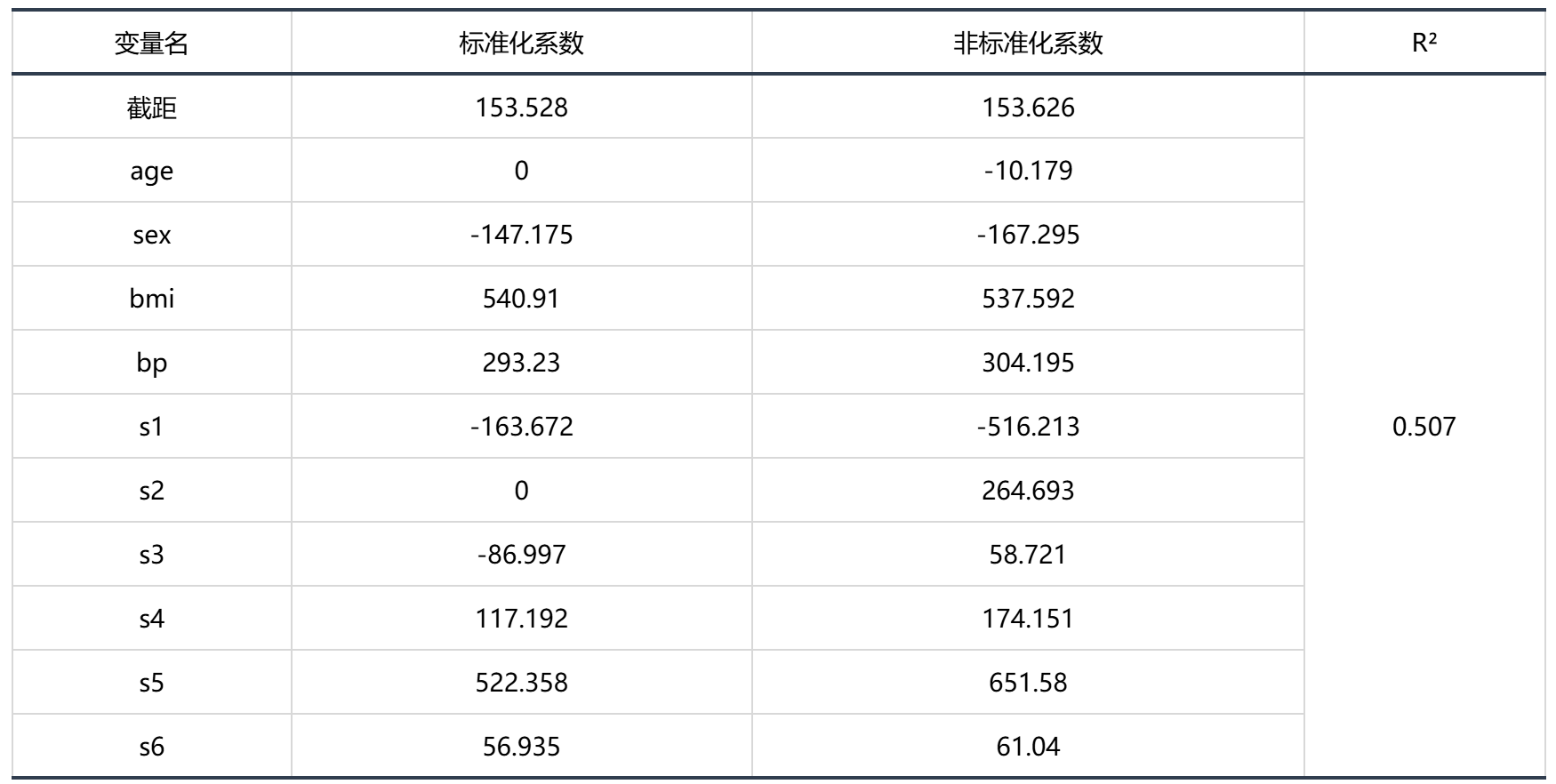

图表说明：上表展示了模型系数情况，当模型中标准化变量系数为 0 时，代表这个变量被排除出模型。
智能分析：
Lasso 回归的结果显示：
基于变量截距项、age、sex、bmi、bp、s1、s2、s3、s4、s5、s6的标准化系数，变量截距项、sex、bmi、bp、s1、s3、s4、s5、s6被保留，age、s2变量被删除。
模型的标准化公式：y=153.528-147.175 × sex+540.91 × bmi+293.23 × bp-163.672 × s1-86.997 × s3+117.192 × s4+522.358 × s5+56.935 × s6。
模型的非标准化公式：y=153.626-10.179 × age-167.295 × sex+537.592 × bmi+304.195 × bp-516.213 × s1+264.693 × s2+58.721 × s3+174.151 × s4+651.58 × s5+61.04 × s6。
分析：Lasso 模型主要用于变量的筛选，筛选的标准是标准化系数是否为 0，可以看到 age、S2 两个变量是不重要的，被排除出模型。

输出结果 4：模型结果图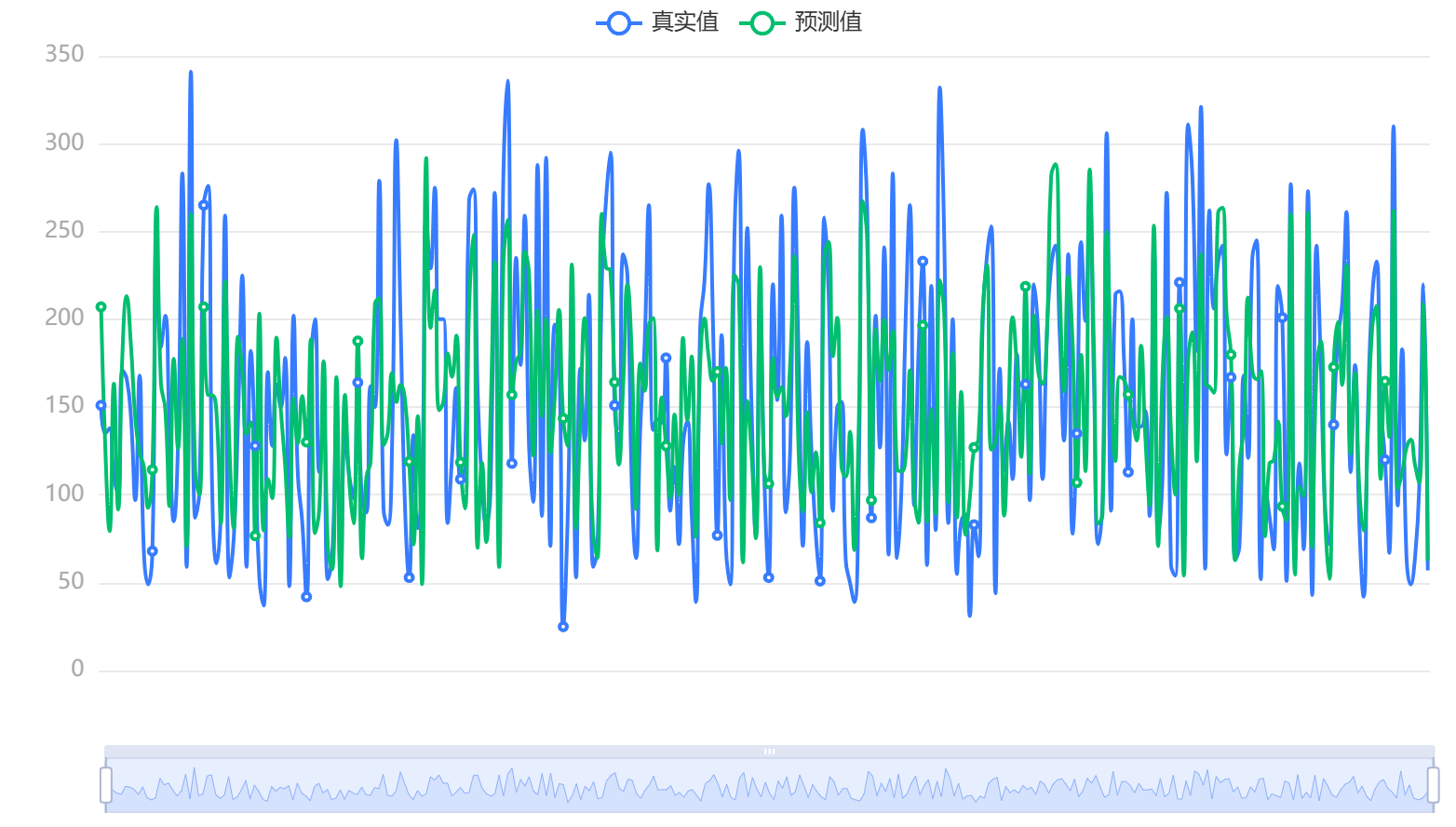

图表说明：上图展示了本次模型的原始数据图、模型拟合值、模型预测值。

输出结果 5：模型结果预测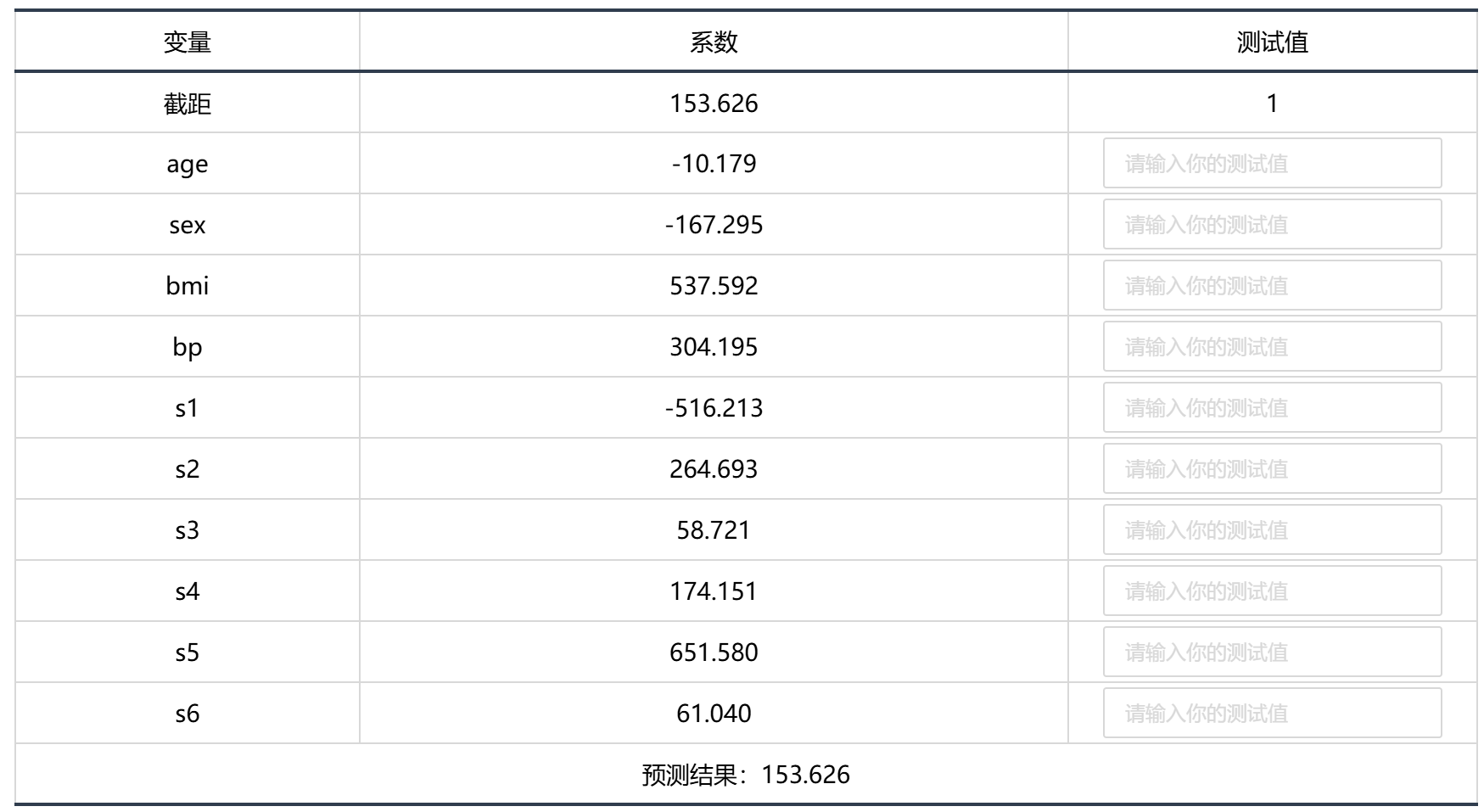

图表说明：上表格显示了经过 Lasso 回归后的模型预测情况。

# 7、注意事项

• 一般会先对数据中心标准化，再进行 Lasso 回归的处理，SPSSPRO 在运算时已经进行了标准化，故不需要再进行标准化。
• Lasso回归主要用于变量的筛选，如果数据并没有共线性，依旧建议使用普通线性最小二乘法回归。
• Lasso使用 L1 正则化，岭回归使用 L2 正则化，L1 可以让一部分特征的系数缩小到 0，从而间接实现特征选择，所以 L1 适用于特征之间有关联的情况。L2 让所有特征的系数都缩小，但是不会减为 0，它会使优化求解稳定快速，所以 L2 适用于特征之间没有关联的情况。
• 在使用Lasso时，部分特征的系数可能会被推到零，这种稀疏性特性使得模型更简单且易于解释。但需要注意，这可能会丢失一些重要的信息，因此需要权衡模型的稀疏性和预测性能。
• Lasso回归在特征数量较少的情况下表现良好，岭回归在特征数量庞大的情况下表现更佳。
• Lasso回归执行“硬阈值化”（hard thresholding）系数，即会将一些特征的系数完全置为零；而岭回归倾向于对系数进行连续收缩（即软阈值化），不会将系数减少到精确为零。

# 8、模型理论

Lasso 回归（Least Absolute Selection and Shrinkage Operator regression）是一种替代最小二乘法的压缩估计方法，全名为最小绝对值选择与收缩算子。Lasso回归的主要目标是在模型简洁性和准确性之间找到平衡。它通过向传统线性回归模型添加惩罚项,即L1正则项来实现这一目标，该惩罚项鼓励产生稀疏解，即某些系数被强制设为0。这一特性使得Lasso能自动识别并丢弃无关或多余的变量，因此在有特征选择需求时可以考虑使用Lasso回归方法。

在Lasso回归中，模型的目标函数被修改为最小化残差平方和加上一个与模型参数绝对值相关的正则化项，这个正则化项通常是一个常数乘以所有模型参数绝对值的总和。

Lasso回归的分析步骤：

1. 线性回归模型。

假设数据$X_i,Y_i$,$X_i=x_1,...,x_n$ 和 $Y_i$ 分别是第 $i$ 个观测值对应的自变量（特征）和因变量（目标）。考虑线性回归模型：

$$y={\beta }_0+\sum _{i=1}^n{\beta }_i{x}_i+ϵ$$

其中，${\beta }_i$是要估计的系数，$ϵ$是误差项。

2. L1 正则化。

Lasso回归中引入了L1惩罚项，该惩罚项的优点是不会像岭回归一样强烈地考虑权重大的参数，它不会优先考虑减少任何特定的模型参数。同时，L1正则化倾向于将某些系数压缩到零，从而促进稀疏性，使得模型中只有少数重要的特征保留，其余特征的系数为零。这种特性使得模型更加简单且易于解释，同时减少了特征选择的需要。L1正则化是系数绝对值之和，乘以调节参数$\lambda$

$$L_1=\lambda ||\theta |{|}_1=\lambda \sum _{i=1}^n|{\theta }_i|$$

其中$\lambda$用于控制正则化的程度，当$\lambda$接近于0，则代表正则化的影响几乎消失，模型更倾向于拟合训练数据，可能会导数过拟合的问题；当$\lambda$增大时，正则化效果加强，可以有效控制模型的复杂度。$\lambda$的取值可以使用交叉验证等方法来选择。

3. 目标函数。

Lasso回归的目标是为了找到使预测值与实际值之间的平方差之和最小化的系数数值。其目标函数为：

$$RSS=\sum _{i=1}^n({\hat{y}}_i-y_i{)}^2$$$$\mathrm{目}\mathrm{标}\mathrm{函}\mathrm{数}=min(RSS+L1)$$

4. 收缩系数（Shrinking coefficients）。收缩系数指的是在回归模型中减少或惩罚系数数值的过程。

通过添加L1正则化项，LASSO回归可以将系数向零收缩。

• 当$\lambda =0$时，所有特征都被考虑，相当于普通的线性回归，仅考虑残差平方和来构建预测模型。
• 当$\lambda$趋向无穷大时，不考虑任何特征，一些系数被推到精确为零,系数为零的变量会被有效地从模型中移除。即随着 λ 趋近无穷大，会逐渐消除更多特征。

偏差（bias）随着 λ 的增加而增加，方差（variance）随着 λ 的减少而增加。

5. 调节参数 $\lambda$。

6. 拟合模型。

# 9、手推步骤

本次手推过程由于初始数据集较大，主要采用前十行数据进行手推分析。基于 $\lambda =0.02$ 计算 $Lasso$ 回归的所有系数，对数据内容进行第一轮迭代的详细推导计算。 $Lasso$ 回归的目标函数为：

$\underset{\beta }{min}\{\sum _{i=1}^n(y_i-{\mathbf{x}}_i^T\beta {)}^2+\lambda \sum _{j=1}^p{\beta }_j\}$

其中$\lambda =0.02，n=10，p=10$。
坐标下降法规则: 对于每个系数${\beta }_j$，公式为：

${\beta }_j\leftarrow \frac{S(\sum _{i=1}^n{x}_{ij}(y_i-{\tilde{y}}_i^{(j)}),\lambda )}{\sum _{i=1}^n{x}_{ij}^2}$

其中软阈值函数：

$S(z,\lambda )=\text{sign}(z)(z-\lambda {)}_{+}$

第1轮迭代计算
(1) ${\beta }_1$（ $age$ 系数）

$\begin{array}{rl}{z}_1& =\sum _{i=1}^{10}{x}_{i1}{y}_i\\ & =0.005383\times 135+(-0.045473)\times 138+\cdots +(-0.017648)\times 123\\ & =-20.8873577\\ S(z_1,0.02)& =-20.8873577+0.02=-20.8673577\\ {\beta }_1& =\frac{-20.8673577}{0.023481}=-888.68\end{array}$

(2) ${\beta }_2$（ $sex$ 系数）

$\begin{array}{rl}{\tilde{y}}_i^{(2)}& =x_{i1}{\beta }_1\\ z_2& =\sum _{i=1}^{10}{x}_{i2}(y_i-{\tilde{y}}_i^{(2)})=15.312\\ S(z_2,0.02)& =15.312-0.02=15.292\\ {\beta }_2& =\frac{15.292}{0.040000}=382.30\end{array}$

(3) ${\beta }_3$（ $bmi$ 系数）

$\begin{array}{rl}{\tilde{y}}_i^{(3)}& =x_{i1}{\beta }_1+x_{i2}{\beta }_2\\ z_3& =\sum _{i=1}^{10}{x}_{i3}(y_i-{\tilde{y}}_i^{(3)})=-13.799\\ S(z_3,0.02)& =-13.799+0.02=-13.779\\ {\beta }_3& =\frac{-13.779}{0.017200}=-801.10\end{array}$

(4) ${\beta }_4$（ $bp$ 系数）

$\begin{array}{rl}{\tilde{y}}_i^{(4)}& =\sum _{j=1}^3{x}_{ij}{\beta }_j\\ z_4& =\sum _{i=1}^{10}{x}_{i4}(y_i-{\tilde{y}}_i^{(4)})=5.632\\ S(z_4,0.02)& =5.632-0.02=5.612\\ {\beta }_4& =\frac{5.612}{0.012800}=438.44\end{array}$

(5) ${\beta }_5$（ $s_1$ 系数）

$\begin{array}{rl}{\tilde{y}}_i^{(5)}& =\sum _{j=1}^4{x}_{ij}{\beta }_j\\ z_5& =\sum _{i=1}^{10}{x}_{i5}(y_i-{\tilde{y}}_i^{(5)})=1.203\\ S(z_5,0.02)& =1.203-0.02=1.183\\ {\beta }_5& =\frac{1.183}{0.009200}=128.59\end{array}$

(6) ${\beta }_6$（ $s_2$ 系数）

$\begin{array}{rl}{\tilde{y}}_i^{(6)}& =\sum _{j=1}^5{x}_{ij}{\beta }_j\\ z_6& =\sum _{i=1}^{10}{x}_{i6}(y_i-{\tilde{y}}_i^{(6)})=0.032\\ S(z_6,0.02)& =0.032-0.02=0.012\\ {\beta }_6& =\frac{0.012}{0.011500}=1.04\end{array}$

(7) ${\beta }_7$（ $s_3$ 系数）

$\begin{array}{rl}{\tilde{y}}_i^{(7)}& =\sum _{j=1}^6{x}_{ij}{\beta }_j\\ z_7& =\sum _{i=1}^{10}{x}_{i7}(y_i-{\tilde{y}}_i^{(7)})=-0.957\\ S(z_7,0.02)& =-0.957+0.02=-0.937\\ {\beta }_7& =\frac{-0.937}{0.008900}=-105.28\end{array}$

(8) ${\beta }_8$（ $s_4$ 系数）

$\begin{array}{rl}{\tilde{y}}_i^{(8)}& =\sum _{j=1}^7{x}_{ij}{\beta }_j\\ z_8& =\sum _{i=1}^{10}{x}_{i8}(y_i-{\tilde{y}}_i^{(8)})=0.021\\ S(z_8,0.02)& =0.021-0.02=0.001\\ {\beta }_8& =\frac{0.001}{0.009800}=0.10\end{array}$

(9) ${\beta }_9$（ $s_5$ 系数）

$\begin{array}{rl}{\tilde{y}}_i^{(9)}& =\sum _{j=1}^8{x}_{ij}{\beta }_j\\ z_9& =\sum _{i=1}^{10}{x}_{i9}(y_i-{\tilde{y}}_i^{(9)})=0.015\\ S(z_9,0.02)& =0(\text{因}0.015<0.02)\\ {\beta }_9& =0\end{array}$

(10) ${\beta }_{10}$（ $s_6$ 系数）

$\begin{array}{rl}{\tilde{y}}_i^{(10)}& =\sum _{j=1}^9{x}_{ij}{\beta }_j\\ z_{10}& =\sum _{i=1}^{10}{x}_{i10}(y_i-{\tilde{y}}_i^{(10)})=0.251\\ S(z_{10},0.02)& =0.251-0.02=0.231\\ {\beta }_{10}& =\frac{0.231}{0.010300}=22.43\end{array}$

第1轮迭代结果:

$\beta ={\left[\begin{array}{ccccc}-888.68& 382.30& -801.10& 438.44& 128.59\\ 1.04& -105.28& 0.10& 0& 22.43\end{array}\right]}^T$

所得的标准化模型为：${\hat{y}}_{\text{std}}=-888.68\cdot x_{\text{age}}+382.30\cdot x_{\text{sex}}-801.10\cdot x_{\text{bmi}}+438.44\cdot x_{\text{bp}}+128.59\cdot x_{\text{s1}}+1.04\cdot x_{\text{s2}}-105.28\cdot x_{\text{s3}}+0.10\cdot x_{\text{s4}}+22.43\cdot x_{\text{s6}}$

通过计算，非标准模型为：$\hat{y}=0.0381\cdot \text{age}+0.0507\cdot \text{sex}+0.0617\cdot \text{bmi}+0.0219\cdot \text{bp}-0.0442\cdot \text{s1}-0.0348\cdot \text{s2}-0.0434\cdot \text{s3}-0.0026\cdot \text{s4}+0.0199\cdot \text{s5}-0.0176\cdot \text{s6}$

以此类推计算，我们进行多几轮的迭代计算，最后可以确定得到 $Lasso$ 回归的预测结果值。

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]柯郑林. Lasso 及其相关方法在多元线性回归模型中的应用[D].北京交通大学,2011.