逻辑回归

操作视频

# 1、作用

逻辑回归（Logistic regression）是一种线性回归分析模型，属于有监督学习的分类模型，主要用于二分类问题，即研究二分类因变量与一些影响因素之间关系的一种多变量分析方法，如果是多分类问题，则要用到多分类逻辑回归去研究因变量与一些影响因素之间的关系。逻辑回归直接建模分类可能性，无需假设数据分布，避免了假设分布不准确的问题。它提供近似概率预测而非仅仅类别预测，对于需要概率辅助决策的任务尤为有用。逻辑回归函数是任意阶可导的凸函数，具有良好的数学性质，适用于现有多种数值优化算法，可高效求解最优解。对于线性数据，逻辑回归在大部分情况下拟合速度较快，计算效率优于支持向量机（SVM）和随机森林（Random Forest）。

# 2、输入输出描述

输入：因变量 Y 为分类变量，自变量 X 为至少一项定量变量或定类变量。
输出：逻辑回归系数估计以及分类预测的效果评价。

# 3、案例示例

示例：根据年龄、月收入、性别、家庭人口等影响因素（自变量）来研究工薪群体的上下班交通工具是公交地铁、自行车、还是私家车（因变量）。

# 4、案例数据

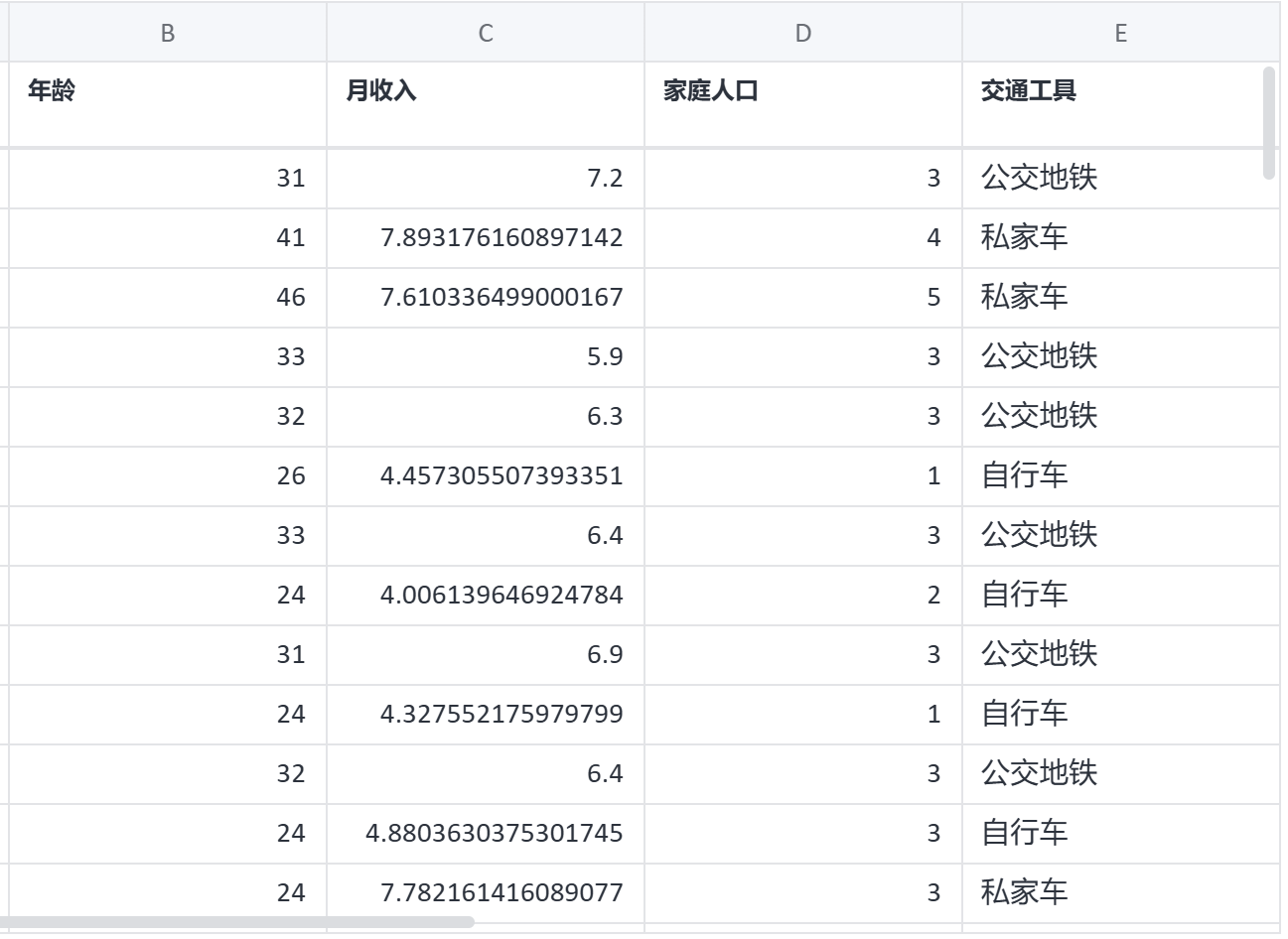
逻辑回归案例数据

# 5、案例操作

Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

step4：选择【逻辑回归】；
step5：查看对应的数据数据格式，按要求输入【逻辑回归】数据;
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：多分类因变量基本汇总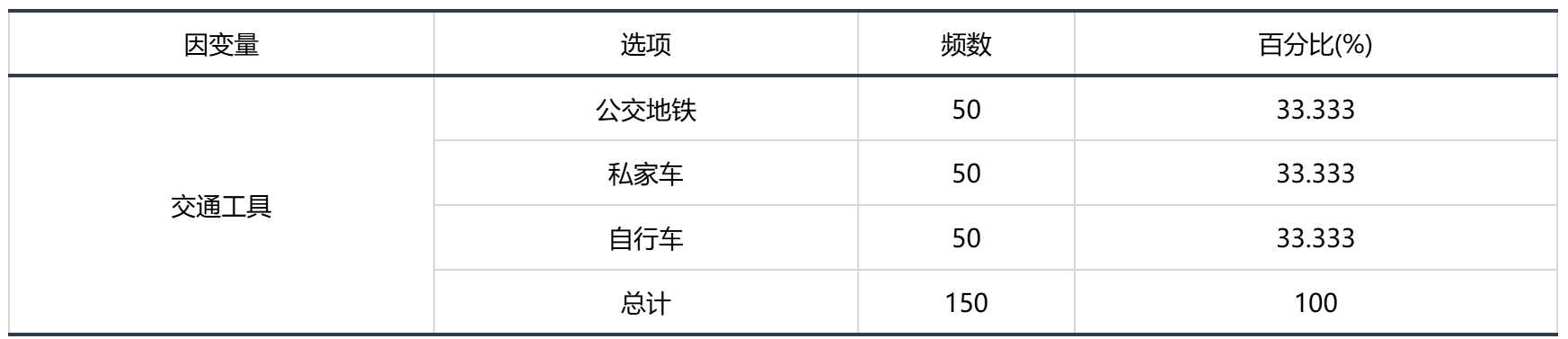
图表说明：上表展示了因变量各分组的分布情况。
由表可知，因变量各分类水平的百分比都相同，说明各分类的样本是很均衡的，不需要进行过采样或欠采样，可以接着做逻辑回归。

输出结果 2：模型评价
图表说明：表展示了模型评价指标，可用于对模型的表现进行评估或有效性进行验证，其包括似然比检验，p 值，AIC 值、BIC 值。
● 对 p 值进行分析，如果该值小于 0.05，则说明模型有效；反之则说明模型无效。
● AIC 值和 BIC 值用于对比两个模型的优劣时使用，此两个值均为越小越好。
分析：模型的似然比卡方检验的结果显示，显著性 𝑝 值 0.000***，水平上呈现显著性，拒绝原假设，因而模型是有效的。

输出结果 3：多分类逻辑回归结果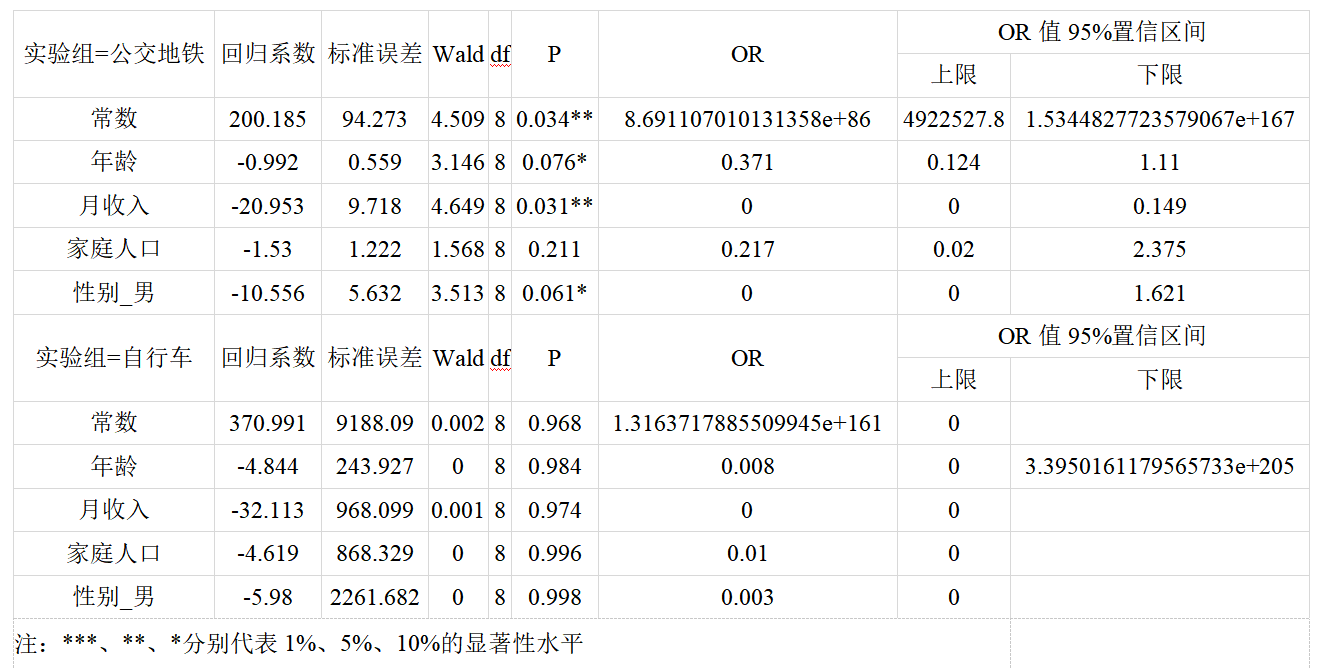
图表说明：上表展示了模型的参数结果，可用于生成模型公式。包括模型的系数、标准误差、OR 值、置信区间等。
● OR 值（优势比）：为实验组的事件发生几率/对照组的事件发生几率。
● 对于连续自变量的 OR 值的意义为：该变量每升高一个单位，发生实验组事件的几率比发生对照组事件的几率变化了（OR 值-1）%。
● 对于哑变量化的 0-1 分类自变量的 OR 值意义为：该变量每升高一个单位（即分类水平从 0 变为 1），发生实验组事件的几率比发生对照组事件的几率变化了（OR 值-1）%。

分析：对于多分类逻辑回归，需要选择有一个分类水平作为基水平，分别对这个基水平去其他分类水平建立二分类逻辑回归，在本例中，选择了“私家车”作为基水平，分别建立了“私家车-公交地铁”和“私家车-自行车”这两个二分类逻辑回归器。

基于参考私家车->公交地铁：
字段常数显著性P值为0.034**，水平上呈现显著性，拒绝原假设，因此常数会对交通工具产生显著性影响，意味着常数每增加一个单位，交通工具为公交地铁的概率比私家车的概率高了8.691107010131357e+88%。
字段年龄显著性P值为0.076*，水平上不呈现显著性，不能拒绝原假设，因此年龄不会对交通工具产生显著性影响。
字段月收入显著性P值为0.031**，水平上呈现显著性，拒绝原假设，因此月收入会对交通工具产生显著性影响，意味着月收入每增加一个单位，交通工具为公交地铁的概率比私家车的概率低了100.0%。
字段家庭人口显著性P值为0.211，水平上不呈现显著性，不能拒绝原假设，因此家庭人口不会对交通工具产生显著性影响。
字段性别_男显著性P值为0.061*，水平上不呈现显著性，不能拒绝原假设，因此性别_男不会对交通工具产生显著性影响。

基于参考私家车->自行车：
字段常数显著性P值为0.968，水平上不呈现显著性，不能拒绝原假设，因此常数不会对交通工具产生显著性影响。
字段年龄显著性P值为0.984，水平上不呈现显著性，不能拒绝原假设，因此年龄不会对交通工具产生显著性影响。
字段月收入显著性P值为0.974，水平上不呈现显著性，不能拒绝原假设，因此月收入不会对交通工具产生显著性影响。
字段家庭人口显著性P值为0.996，水平上不呈现显著性，不能拒绝原假设，因此家庭人口不会对交通工具产生显著性影响。
字段性别_男显著性P值为0.998，水平上不呈现显著性，不能拒绝原假设，因此性别_男不会对交通工具产生显著性影响。

输出结果 4：混淆矩阵热力图

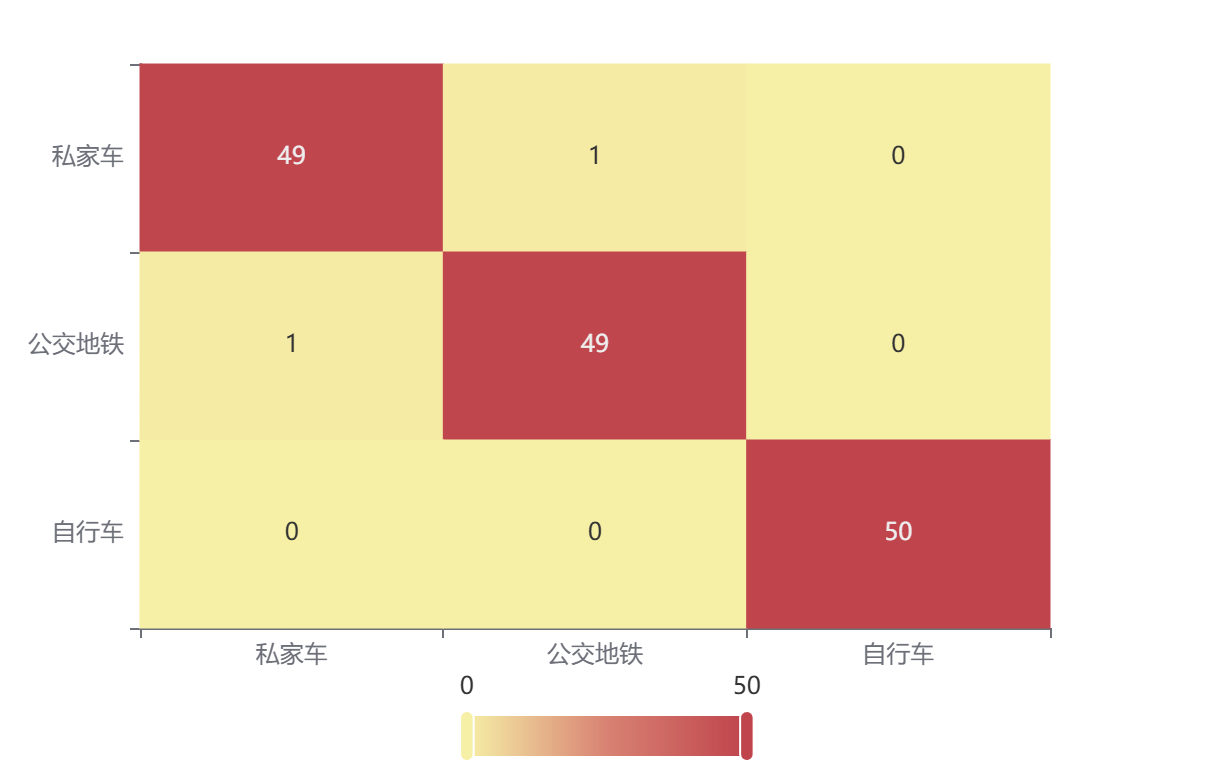
图表说明：上表以热力图的形式展示了混淆矩阵。

输出结果 5：分类评价指标

准确率	召回率	精确率	F1	AUC
0.987	0.987	0.987	0.987	1

图表说明：上表中展示了分类评价指标，进一步通过量化指标来衡量逻辑回归的分类效果。
● 准确率：预测正确样本占总样本的比例，准确率越大越好。
● 召回率：实际为正样本的结果中，预测为正样本的比例，召回率越大越好。
● 精确率：预测出来为正样本的结果中，实际为正样本的比例，精确率越大越好。
● F1：精确率和召回率的调和平均，精确率和召回率是互相影响的，虽然两者都高是一种期望的理想情况，然而实际中常常是精确率高、召回率就低，或者召回率低、但精确率高。若需要兼顾两者，那么就可以用F1指标。
● AUC：AUC值越接近1说明分类效果越好。
注：精确率、召回率、F1值、AUC值是分别度量分类器对某一类别预测结果的评价指标值，后续再对所有类别根据样本进行加权平均后得到整体评价指标值。

# 7、注意事项

对于多分类逻辑回归，spsspro 默认用了将某一类和剩余的类比较作为二分类问题，N 个类别进行 N-1 次分类，得到 N-1 个二分类模型，求出每种二分类对应的概率，概率最高的一类作为新样本的预测结果。
逻辑回归如果有输入定类数据，那么要求该定类数据必须为二分类定类数据（哑变量化），因此 SPSSPRO 的输入变量 X2 中要求数据为定类数据，若数据不为二分类定类数据，SPSSPRO 会自动将其哑变量化。

# 8、模型理论

逻辑回归的基本定义是通过拟合一条直线将不同类别的样本区分开来。其核心思想是使用sigmoid函数把线性回归的结果从 $(- \infty, \infty)$ 映射到 $(0, 1)$ 中。那么，sigmoid函数到底是怎么来的，我们可以做一个简单的推导：

假设我们有一线性回归公式： $y = w^{T} x$

在这里我们假设先验服从伯努利分布（Bernoulli distribution），即只有两种可能结果的随机试验的概率分布，所以：

$p (x = 1) = p$
$p (x = 0) = 1 - p$

所以我们得到伯努利分布的概率质量函数为：

f (x) = p^{x} (1 - p)^{1 - x}

则：

$f (x) = e^{l n p^{x} (1 - p)^{1 - x}}$

$= e^{l n p^{x} + l n (1 - p)^{1 - x}}$

$= e^{x l n p + (1 - x) l n (1 - p)}$

$= e^{x l n p + l n (1 - p) - x l n (1 - p)}$

$= e^{x l n \frac{p}{1 - p} + l n (1 - p)}$

逻辑回归模型假设事件的对数几率（log odds）是输入变量x的线性函数，需要注意的是，这里的参数 $θ$ 的引入是为了通过一个非线性映射将p表示为 $θ$ 的函数，保证p落在[0,1]范围内，即表示概率值。即：

令 $θ = β_{0} + β_{1} x$ , $θ = l n \frac{p}{1 - p}$ ,则:

e^{θ} = e^{l n \frac{p}{1 - p}} = \frac{p}{1 - p}

所以

(1 - p) e^{θ} = e^{θ} - p e^{θ} = p

p = \frac{e^{θ}}{1 + e^{θ}} = \frac{1}{\frac{1}{e^{θ}} + 1} = \frac{1}{1 + e^{- θ}}

将其简化为：

p = σ (β_{0} + β_{1} x)

σ (z) = \frac{1}{1 + e^{- z}}

而这就是sigmoid函数的形式。 我们把它写成一般形式：

σ (x) = \frac{1}{1 + e^{- x}}

其函数图像为：

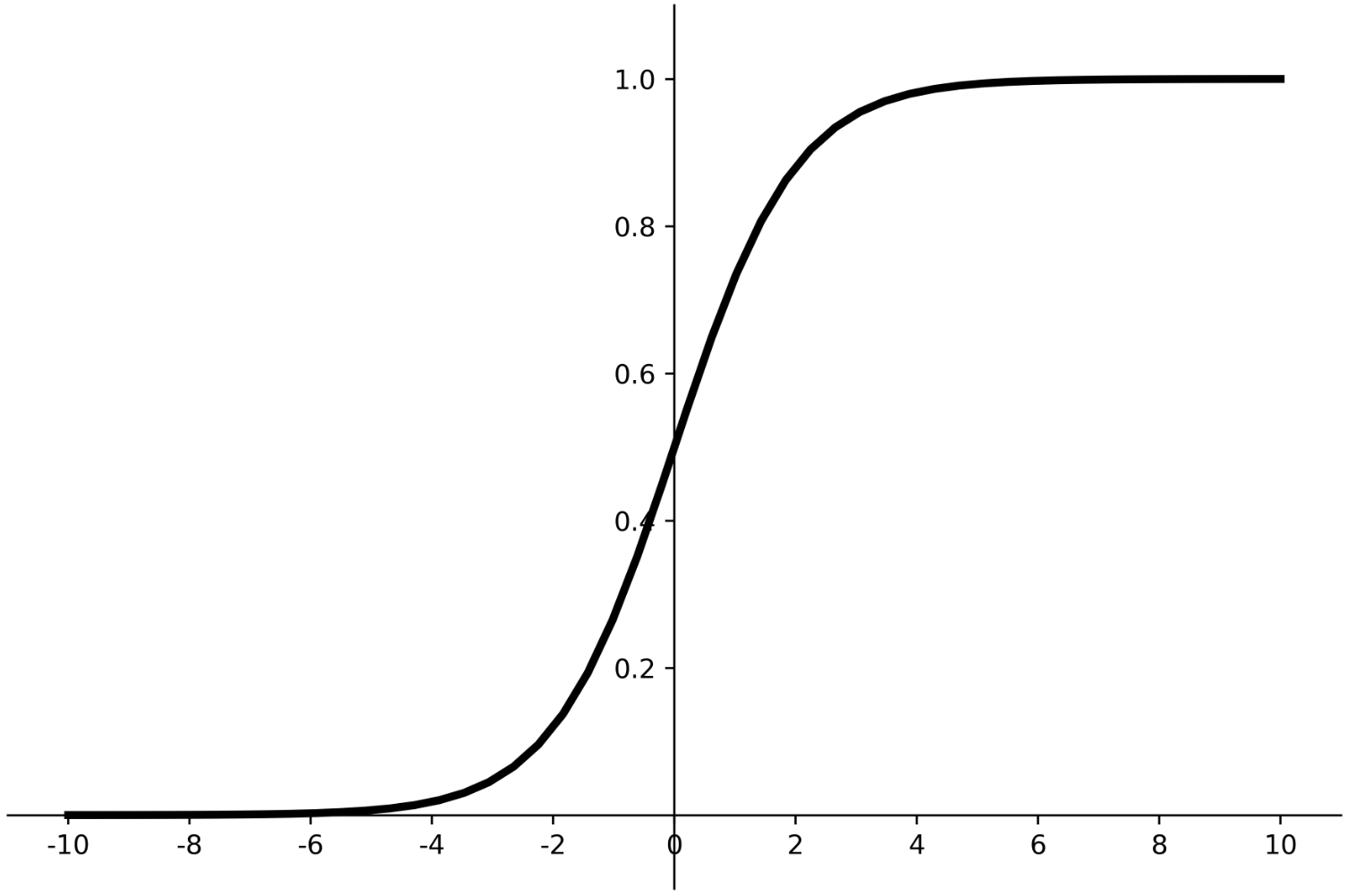
从图中可以看出，当 $x \to \infty$ 时， $σ (x) \to 1$ , 当 $x \to - \infty$ 时， $σ (x) \to 0$ 。

因此，逻辑回归的公式为：

f (x) = \frac{1}{1 + e^{- w^{T} x}}

我们可以用最大似然估计法（Maximum Likelihood Estimation, MLE）来估算函数中的参数 $w$ 。

结合上述式子，令 $g_{w} (y) = \frac{1}{1 + e^{- (w^{T} x + w_{0})}}$ ,我们可以得到: $p (y = 0 | x) = 1 - p (y = 1 | x) = 1 - g_{w} (y)$

则，

p (y | x, w) = (g_{w} (x))^{y} (1 - g_{w} (x))^{1 - y}

假设我们有m个样本，则使用MLE构建函数为：

L (w) = \prod_{i = 1}^{m} p (y_{i} | x_{i}; w) = \prod_{i = 1}^{m} (g_{w} (x_{i}))^{y_{i}} (1 - g_{w} (x_{i}))^{1 - y_{i}}

为了方便计算，我们使用对数似然，将乘法转变为加法运算：

l n (L (w)) = \sum_{i = 1}^{m} (y_{i} l n (g_{w} (x_{i})) + (1 - y_{i}) l n (1 - g_{w} (x_{i})))

因此，我们可以用梯度上升法求解上式对数似然函数，求出使得目前结果的可能性最大的参数 $w$ 。也可以由对数似然函数构造损失函数，用梯度下降法求出使得损失最小对应的参数 $w$ 。在这里，我们构造损失函数：

J (w) = - \frac{1}{m} l n (L (w))

使用梯度下降法求解的核心思想是，先求导找出梯度下降方向，再求解找出要下降多少,即步长。因此，我们先对 $J (w)$ 求关于 $w$ 的偏导求得梯度下降方向：

\frac{\partial J (w)}{\partial w_{j}} = \frac{1}{m} \sum_{i = 1}^{m} [g (w^{T} x_{i}) - y_{i}] * x_{i}^{j}

步长为：

w_{j}^{k + 1} = w_{j}^{k} - a \frac{\partial J (w)}{\partial w_{j}}

注意， $a$ 为学习率，把当前位置的w代入到 $- a \frac{\partial J (w)}{\partial w_{j}}$ 中，才是在该点处梯度下降的步长。当迭代达到一定次数或小于某个阈值时即可停止。

至此，我们完成了逻辑回归的整个过程。

针对于多分类逻辑回归，SPSSPRO 默认用了将某一类和剩余的类(OVR)比较作为二分类问题，N 个类别进行 N-1 次分类，得到 N-1 个二分类模型，求出每种二分类对应的概率，概率最高的一类作为新样本的预测结果。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]袁翔宇,张蓬鹤,熊素琴,等. 基于逻辑回归算法的异常用电辨识方法研究[J]. 电测与仪表,2021,58(12):81-87. DOI:10.19753/j.issn1001-1390.2021.12.012.
[3]On the Rate of Growth of the Population of the United States Since 1790 and its Mathematical RepresentationRaymond Pearl, and Lowell J. ReedPNAS 1920;6;275-288 doi:10.1073/pnas.6.6.275
[4]Trevor Hastie, Robert Tibshirani and Jerome Friedman (2nd ed., 2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. [5]https://cloud.tencent.com/developer/article/1694338

建议反馈