二阶聚类
# 二阶聚类
# 1、作用
二阶聚类也称二步聚类,是使用BIRCH聚类算法的一种聚类分析,其将聚类过程分两步进行。首先创建聚类特征树(CF Tree)对数据集进行预聚类,之后再根据预聚类的结果对样本进行第二次聚类。由于假设模型中的定类和定量变量都服从联合多元正态分布,故可以有效对定类变量聚类。
# 2、输入输出描述
输入:1个或一个以上的定类变量或者定量变量,可选聚类类别数。
输出:聚类总的类别数和样本划分的类别。
# 3、案例示例
案例:根据调研用户的收入、年龄、学历等变量进行聚类。由于学历为定类变量,故选择二阶聚类进行分析。
# 4、案例数据
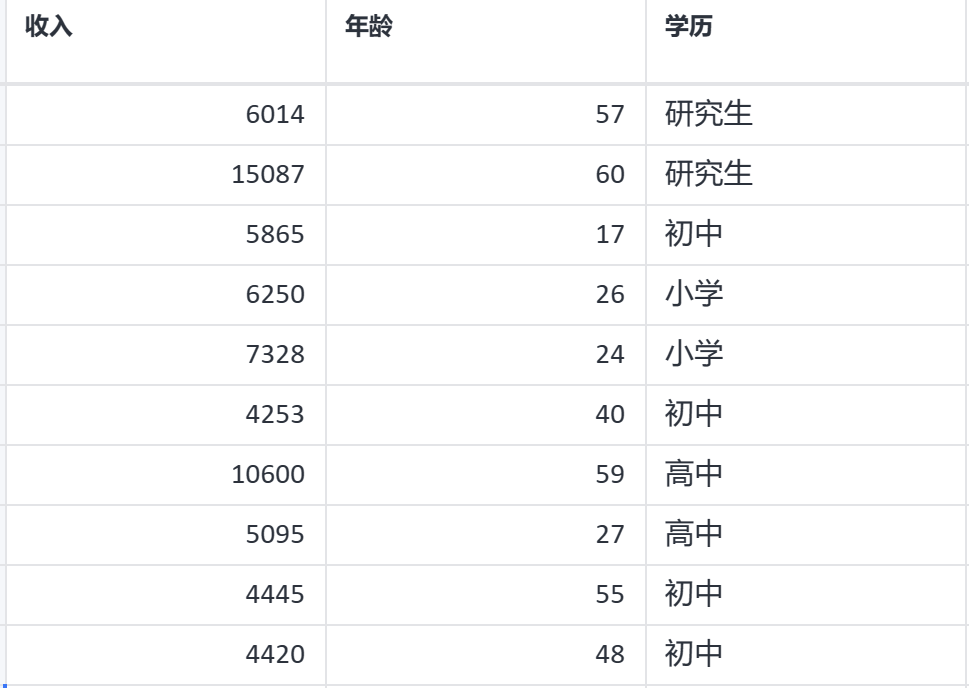
二阶聚类案例数据
# 5、案例操作
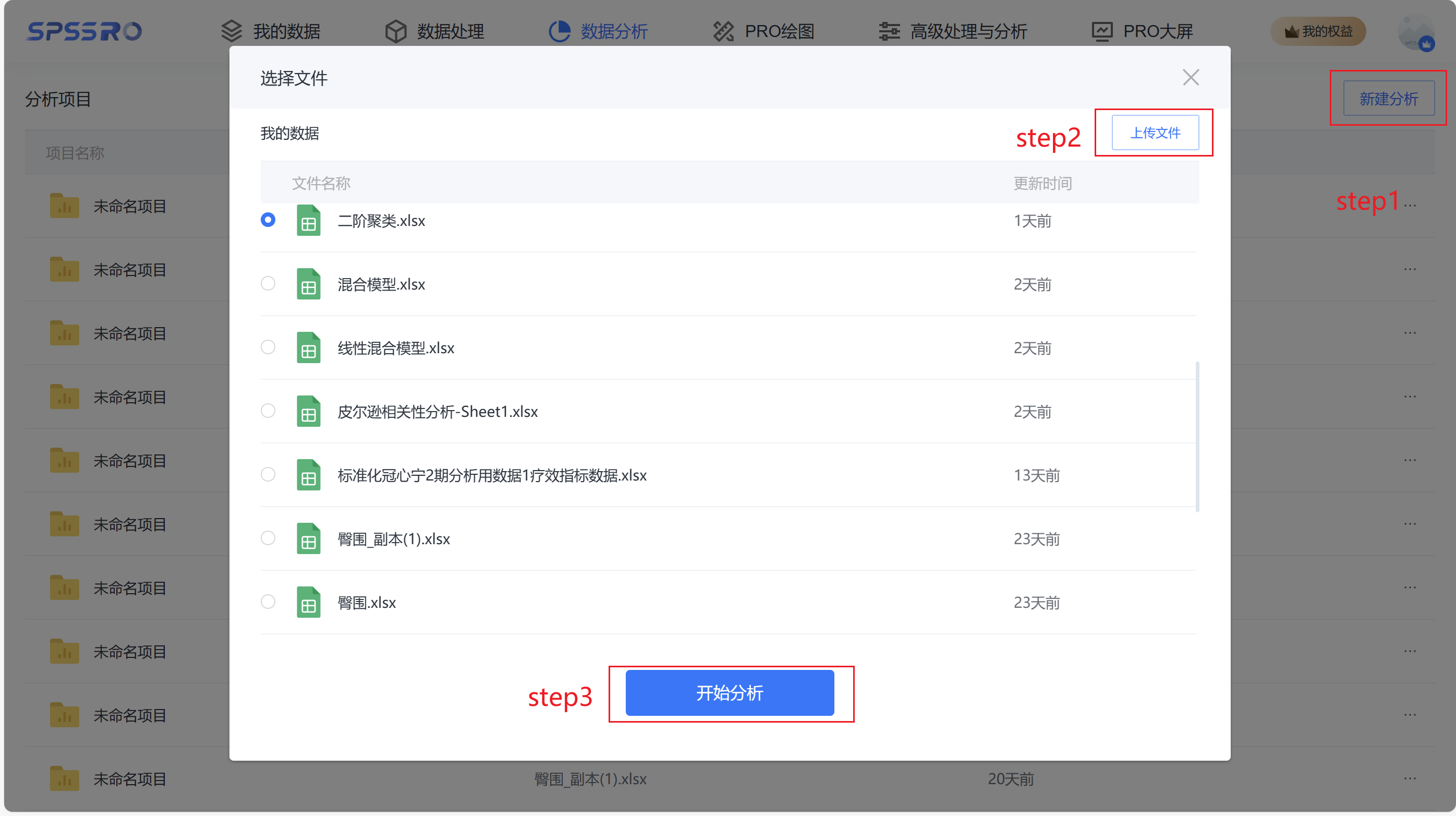
Step1:新建分析;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;
step4:选择【二阶聚类】;
step5:查看对应的数据数据格式,按照【二阶聚类】要求拖入变量;
step6:点击【开始分析】,完成全部操作。
# 6、输出结果分析
输出结果1:聚类情况表
| 聚类数目 | 施瓦兹贝叶斯准则 (BIC) | BIC 变化量 | BIC 变化比率 | distance |
|---|---|---|---|---|
| 1 | 266869.382 | |||
| 2 | 251745.912 | -15123.47 | 1 | 1.347 |
| 3 | 240536.865 | -11209.047 | 0.741 | 1.696 |
| 4 | 233958.262 | -6578.603 | 0.435 | 1.202 |
| 5 | 228497.165 | -5461.097 | 0.361 | 5.663 |
| 6 | 227593.47 | -903.695 | 0.06 | 1.055 |
| 7 | 226740.307 | -853.163 | 0.056 | 1.005 |
| 8 | 225892.096 | -848.211 | 0.056 | 1.057 |
| 9 | 225093.615 | -798.481 | 0.053 | 1.02 |
| 10 | 224312.613 | -781.002 | 0.052 | 3.246 |
| 11 | 224122.958 | -189.655 | 0.013 | 1.118 |
| 12 | 223961.117 | -161.841 | 0.011 | 1.002 |
| 13 | 223799.69 | -161.426 | 0.011 | 1.06 |
| 14 | 223651.615 | -148.075 | 0.01 | 1.277 |
| 15 | 223551.672 | -99.942 | 0.007 | 1.301 |
| 轮廓系数=0.404 |
图表说明:上表展示了不同聚类数的BIC值和变化情况等,用于分析合适的聚类数以及聚类效果。根据聚类情况表的计算得到,合适的聚类个数为5。其中聚类的轮廓系数为0.404,可以认为聚类结果是尚可的。
输出结果2:聚类汇总图
图表说明:上图展示了模型聚类的结果,包括频数,所占百分比。
输出结果3:数据集聚类标注
| 收入 | 年龄 | 学历 | 类别 |
|---|---|---|---|
| 6014 | 57 | 研究生 | 1 |
| 15087 | 60 | 研究生 | 1 |
| 5865 | 17 | 初中 | 3 |
| 6250 | 26 | 小学 | 4 |
| 7328 | 24 | 小学 | 4 |
| 4253 | 40 | 初中 | 3 |
| 10600 | 59 | 高中 | 2 |
| 5095 | 27 | 高中 | 2 |
| 4445 | 55 | 初中 | 3 |
| 4420 | 48 | 初中 | 3 |
| 4293 | 33 | 初中 | 3 |
| 4042 | 33 | 初中 | 3 |
| 10136 | 15 | 大学 | 5 |
| 3324 | 49 | 小学 | 4 |
| 8850 | 26 | 大学 | 5 |
图表说明:上表展示了数据聚类的类别标注。 若是结果超过15行数据,点击表格右上角的下载按钮去导出全部结果。
输出结果4:定量变量聚类中心点坐标
| 1 | 2 | 3 | 4 | 5 | 合计 | |
|---|---|---|---|---|---|---|
| 中心值_收入 | 15489.729 | 6008.021 | 4500.924 | 5460.99 | 8964.805 | 40424.468 |
| 中心值_年龄 | 38.262 | 38.71 | 38.138 | 37.719 | 38.145 | 190.974 |
图表说明:上表展示了在不同聚类种类中定量变量的中心值情况。
由“中心值_收入”可以看到,不同类别的收入差别是较大的,收入最高的是类别1,说明收入对聚类结果影响较大;
由“中心值_年龄”可以看到,不同类别的年龄均值是比较接近的,说明年龄对聚类结果的影响不大;
输出结果5:定类变量分布情况
| 学历 | 1 | 2 | 3 | 4 | 5 | 合计 |
|---|---|---|---|---|---|---|
| 研究生 | 1968 | 0 | 0 | 0 | 0 | 1968 |
| 初中 | 0 | 0 | 2024 | 0 | 0 | 2024 |
| 小学 | 0 | 0 | 0 | 1944 | 0 | 1944 |
| 高中 | 0 | 2033 | 0 | 0 | 0 | 2033 |
| 大学 | 0 | 0 | 0 | 0 | 2031 | 2031 |
图表说明:上表展示了在不同聚类种类中定类变量不同水平的分布情况。由学历这个变量,可以看到,二阶聚类聚成的5类依次对应了学历的五个水平,说明学历对聚类结果影响较大;
# 7、注意事项
- 系统聚类结果基于BIC准则判断;
# 8、模型理论
两阶聚类就是为分成两步来完成聚类过程,可同时基于类别变量和连续变量进行聚类;:
第一步对所有记录进行距离考察,构建CF分类特征树,同一个树节点内的记录相似度高,相似度差的记录则会生成新的节点。
第二步,在分类树的基础上,使用凝聚法对节点进行分类,每一个聚类结果使用BIC或者AIC进行判断,得出最终的聚类结果。
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 李玲静, 汪存友, 余嘉元. 对两阶聚类法自动确定聚类数规则的求证[J]. 统计与决策, 2010(20):2.
[3] 祝迎春. 二阶聚类模型及其应用[J]. 市场研究, 2005(1):3.
