混合模型
# 混合模型
# 1、作用
混合模型用于估计固定效用对因变量Y的影响水平以及随机效应对因变量Y的影响差异。
# 2、输入输出描述
输入:1个定量因变量、固定变量、随机变量。
输出:固定效应水平和随机效应方差结果。
# 3、案例示例
案例:假设你正在研究不同植物品种在不同环境条件下的生长。你有一个数据集,其中包括以下信息:
固定效应:不同植物品种(假设有3个品种)。
随机效应:不同生长箱(假设有4个生长箱)和不同施肥水平(假设有2个水平)。
使用线性混合模型来分析这些数据,考虑到不同植物品种、施肥水平和生长箱对植物生长的影响。
# 4、案例数据

混合模型案例数据
# 5、案例操作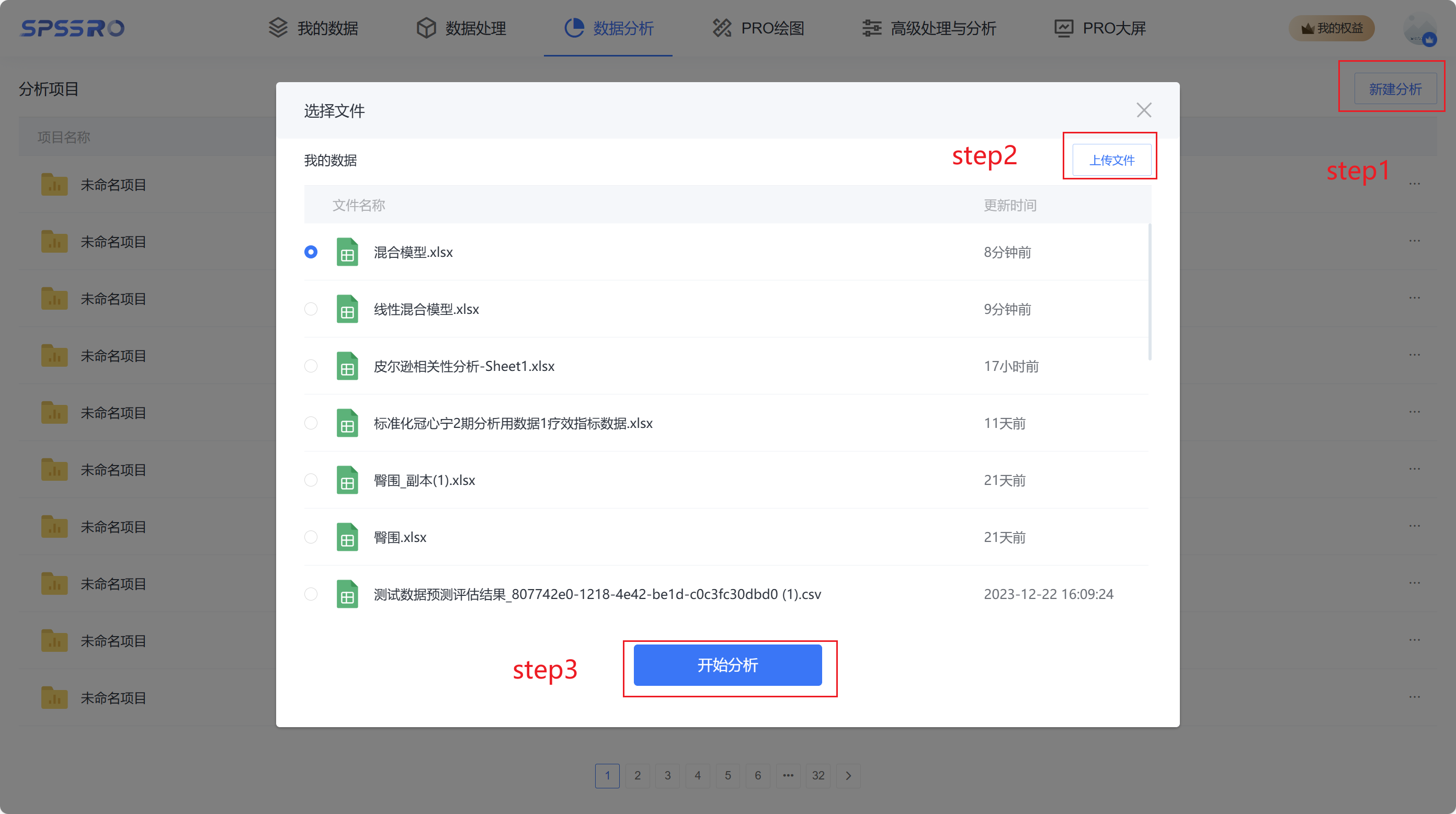
Step1:新建分析;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;
step4:选择【混合模型】;
step5:查看对应的数据数据格式,按照【混合模型】要求拖入变量
step6:点击【开始分析】,完成全部操作。
# 6、输出结果分析
输出结果1:固定效应检验
| 项 | 分子自由度 | F | P |
|---|---|---|---|
| PlantVariety | 2 | 1.135 | 0.326 |
图表说明:上表展示了固定效应检验的结果,可以确定固定变量是否与因变量存在显著关联。 对于PlantVariety,F检验的显著性P值为0.326,水平上不呈现显著性,说明PlantVariety对Growth没有显著性影响。
输出结果2:固定效应估计结果 
图表说明:上表是固定效用的估计结果。
(1)对于定量固定变量,固定效应的估计值表示每个定量变量单位的变化对因变量的平均影响。
(2)对于定类固定变量来说,固定效应的估计值表示相对于基准类别的平均差异(如果说某个因子有三个类别:A/B/C,以A作为基准类别,可以求出B/C的估计值):
● 如果估计值为正,表示相应的类别相对于基准类别在因变量上有正的平均差异;
● 如果估计值为负,表示相应的类别相对于基准类别在因变量上有负的平均差异。
输出结果3:随机效应方差估计结果
图表说明:上表是随机效用方差估计结果,随机效应的方差代表该变量对于因变量Y影响时,不同组别之间是否有着差异性。
# 7、注意事项
- 选择固定效应变量还是随机效应变量取决于你对研究问题的理解、研究设计以及数据的特点。以下是一些指导原则:
(1)固定效应变量:如果你感兴趣的是研究样本中的个体之间的差异,而不是对整个人群进行推断,通常选择固定效应变量。例如,如果你想知道不同个体之间的特征对于某种结果的影响程度,固定效应模型可以提供对个体之间差异的更详细的解释。
(2)随机效应变量:如果你感兴趣的是对整个人群的推断,但是认识到个体之间可能存在随机差异,或者希望通过随机效应考虑个体之间的相关性,可以选择随机效应变量。随机效应模型可以更好地处理个体间的随机差异,提供更稳健和更一般化的推断。
# 8、模型理论
混合线性模型是一种考虑了固定效应和随机效应的线性模型,公式如下: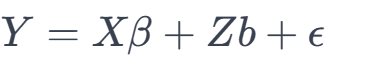

- Y 是因变量向量。
- X 是固定效应的设计矩阵。
- β 是固定效应的参数向量。
- Z 是随机效应的设计矩阵。
- b 是随机效应的参数向量,满足 )b_∼_N(0,G),其中 G 是随机效应的协方差矩阵。
- ϵ 是误差项,满足 ϵ_∼_N(0,R),其中 R 是误差项的协方差矩阵。
固定效应:Xβ 表示固定效应对因变量的影响。这部分效应是我们感兴趣的,因为它反映了在整个样本中固定效应的平均影响。
随机效应:Zb 表示随机效应对因变量的影响。这部分效应用于解释不同层次之间的变异性,例如不同个体之间的差异。
误差项:ϵ 表示未被模型考虑的其他因素对因变量的影响,以及由于测量误差引起的变异。
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
