典型相关分析

# 1、作用

典型相关分析是研究多个变量和多个变量之间的线性相关关系，能够揭示出两组变量之间的内在联系。首先在每组变量中找到变量的线性组合，使得两组的线性组合之间具有最大的相关系数。然后选取和最初挑选的这对线性组合不相关的线性组合，使其配对，并选取相关系数最大的那一组。如此继续配对，直到两组变量之间的相关性被提取完。

# 2、输入输出描述

输入：集合 Y 为至少两项或以上的定量变量或有序定类变量
输出：成对典型变量的相关性，以及典型变量对研究变量的解释比例。

# 3、案例示例

案例：研究 200 名大学生四个学术得分变量与三个心理得分变量之间的关系。

# 4、案例数据

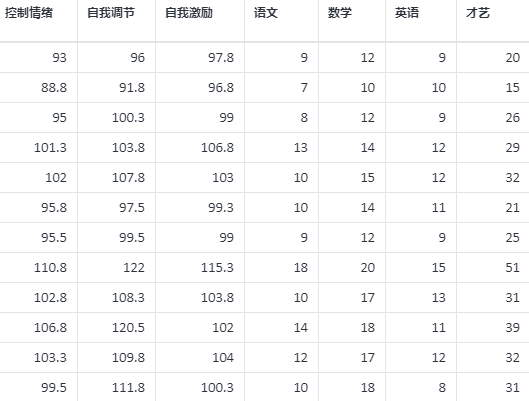
典型相关分析案例数据

# 5、案例操作

Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；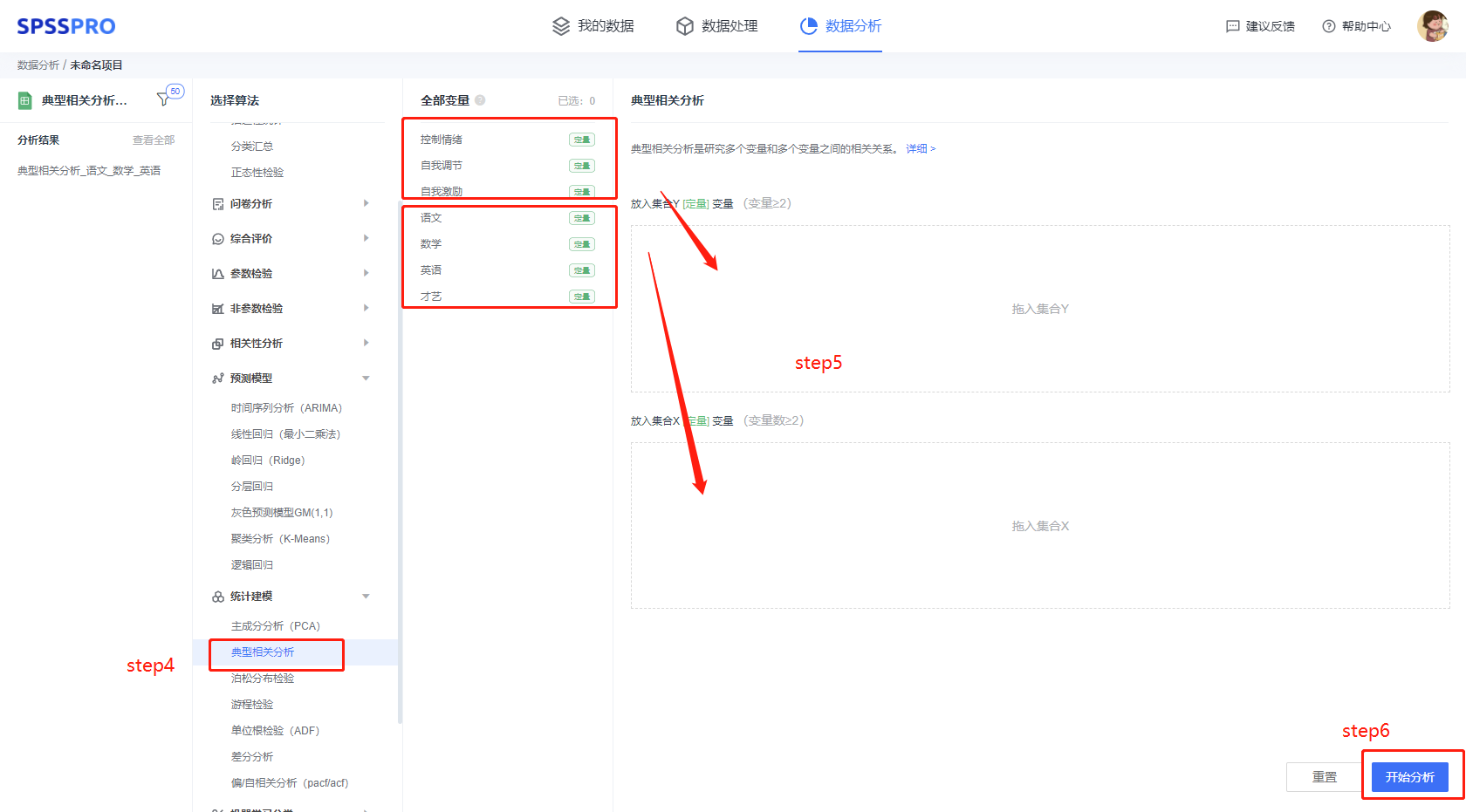

step4：选择【典型相关分析】；
step5：查看对应的数据数据格式，按要求输入【典型相关分析】数据。
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：典型相关系数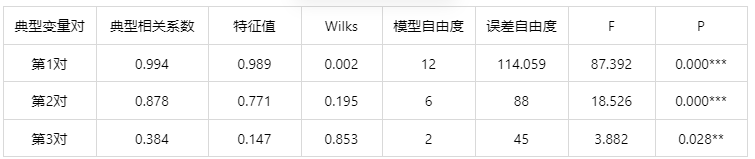

分析：由上表可知，前 3 对典型变量通过显著性检验，认为前 3 对典型变量之间的相关性显著，第 1 对典型变量的相关系数为 0.994。第 2 对典型变量的相关系数为 0.878。第 3 对典型变量的相关系数为 0.384。第一对典型变量贡献率为 0.989/（0.989+0.771+0.147）=51.9%，第二对典型变量贡献率为 0.771/（0.989+0.771+0.147）=40.4%，所以第一对和第二对典型变量的总贡献率达到 92.3%，因此后续分析重点关注第一对和第二对典型变量。
注意：这里 p 值显著以典型相关系数大小没有必然的联系，p 值显著，说明典型变量间不相关的概率很小，即典型变量间大概率是相关的，至于多大的相关程度是不能判断的。

输出结果 2：典型变量系数

集合 Y 典型变量系数

	典型变量 Y1	典型变量 Y2	典型变量 Y3
控制情绪	0.062	0.174	0.377
自我调节	0.021	-0.242	-0.104
自我激励	0.078	0.238	-0.383

集合 X 典型变量系数

	典型变量 X1	典型变量 X2	典型变量 X3
语文	0.07	0.192	-0.247
数学	0.031	-0.202	0.142
英语	0.09	0.496	0.28
才艺	0.063	-0.068	-0.011

图表说明：上表展示了典型变量的系数，可得到典型变量的组成公式。
集合 Y 的第 1 典型变量的计算公式：Y1=0.062× 控制情绪+0.021× 自我调节+0.078× 自我激励
集合 Y 的第 2 典型变量的计算公式：Y2=0.174× 控制情绪-0.242× 自我调节+0.238× 自我激励
集合 Y 的第 3 典型变量的计算公式：Y3=0.377× 控制情绪-0.104× 自我调节-0.383× 自我激励
集合 X 的第 1 典型变量的计算公式：X1=0.07× 语文+0.031× 数学+0.09× 英语+0.063× 才艺
集合 X 的第 2 典型变量的计算公式：X2=0.192× 语文-0.202× 数学+0.496× 英语-0.068× 才艺
集合 X 的第 3 典型变量的计算公式：X3=-0.247× 语文+0.142× 数学+0.28× 英语-0.011× 才艺

输出结果 3：典型负荷系数和交叉负荷系数
集合 Y 典型载荷系数和交叉载荷系数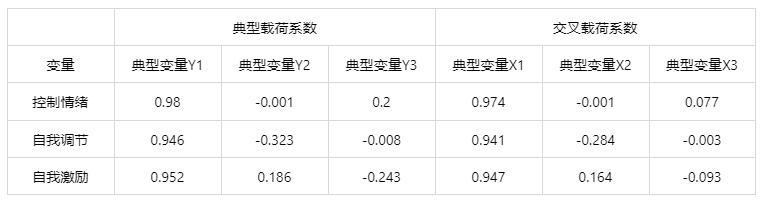

集合 X 典型载荷系数和交叉载荷系数

图表说明：上表展示了典型载荷系数和交叉载荷系数 ，典型载荷系数绝对值越大说明该项与典型变量之间的相关关系越强。
● 典型载荷系数是指一个典型变量与本组所有变量的简单相关系数。
● 交叉载荷系数是指一个典型变量与另一组变量各个变量的简单相关系数。

输出结果 4：载荷矩阵热力图

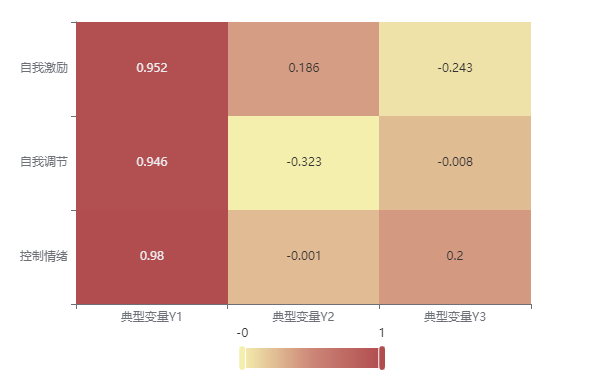
分析：以上是集合 Y 典型载荷矩阵热力图，由图可知，典型变量 Y1 与集合 Y 里面的三个心理得分变量（自我激励、自我调节、控制情绪）的相关性较高，说明典型变量 1 就能很好地解释集合 Y 中心理得分的三个变量。典型变量 2 更多解释了“自我调节”这个变量。

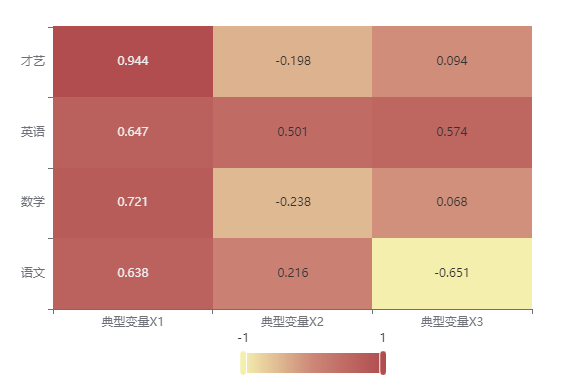
分析：以上是集合 X 典型载荷矩阵热力图，由图可知，典型变量 X1 就能很好地解释集合 X 中学术得分的四个变量，尤其是才艺这个变量，它与典型变量 X1 具有极高的向相关性。典型变量 X2 更多地解释集合 X 中“英语”这个变量。
**图表说明**：上图展示了载荷矩阵热力图，可以直观看出典型变量与本组所有变量的相关性或典型变量与另一组变量的相关性。主要通过颜色深浅去表示值的大小。

输出结果 5：方差解释比例

	集合X(%)	集合Y(%)
典型变量X1	55.944	92.063
典型变量X2	9.833	4.632
典型变量X3	19.188	3.305
典型变量Y1	91.05	55.329
典型变量Y2	3.572	7.582
典型变量Y3	0.486	2.824

图表说明：上表中展示了典型变量的解释比例，包括组内解释比例和交叉解释比例，定量地判断典型变量所包含的原始信息量的大小。
智能分析：
典型变量 X1 解释了集合 Y 中指标的 92.063%信息量，解释了集合 X 中指标的 55.944%信息量。
典型变量 X2 解释了集合 Y 中指标的 4.632%信息量，解释了集合 X 中指标的 9.833%信息量。
典型变量 X3 解释了集合 Y 中指标的 3.305%信息量，解释了集合 X 中指标的 19.188%信息量。
典型变量 Y1 解释了集合 Y 中指标的 55.329%信息量，解释了集合 X 中指标的 91.05%信息量。
典型变量 Y2 解释了集合 Y 中指标的 7.582%信息量，解释了集合 X 中指标的 3.572%信息量。
典型变量 Y3 解释了集合 Y 中指标的 2.824%信息量，解释了集合 X 中指标的 0.486%信息量。
分析：这一步主要是为了进行冗余分析，如果一个变量可以由另一个变量的方差来解释或者预测，那么就说这方差部分与另一变量方差冗余。可以计算求出典型变量对的共享方差

• 第一典型变量（小数相乘转百分比）：$(0.55944\times 0.92063)\times 100\mathrm{\%}\approx 51.40\mathrm{\%}$
• 第二典型变量（小数相乘转百分比）：$(0.09833\times 0.04632)\times 100\mathrm{\%}\approx 0.4555\mathrm{\%}$
• 第三典型变量（小数相乘转百分比）：$(0.19188\times 0.03305)\times 100\mathrm{\%}\approx 0.6342\mathrm{\%}$

# 7、注意事项

• 典型相关系数是矩阵 X 和 Y 相应特征向量的求解，有可能与其他标准结果出现系数相反的情况。

# 8、模型理论

我们假设两个变量的集合 和 ：

定义两个线性关系的集合 和 ， 是 的线性组合， 是 的线性组合：

我们希望找到使得在每一对和 中关联关系最大的线性组合。
定义 的方差如下：

定义 的方差计算如下：

最后 和 的协方差计算如下：

我们采用如下方式来判断 和 的相关性：

我们的目的就是要最大化 。我们想找到关于 和 的线性组合，使他们上述的关联关系最大化。

这个函数优化一般有两种方法，第一种是奇异值分解 SVD，第二种是特征分解，两者得到的结果一样。

# 9、手推步骤

# Step 1:基本统计量（均值与标准差）

变量	均值	标准差
控制情绪	99.326	8.319
自我调节	106.244	9.875
自我激励	102.732	5.241
语文	10.98	3.642
数学	13.92	3.831
英语	10.24	2.502
才艺	29.14	10.743

标准化公式：

$z=\frac{x-\overline{x}}{s}$

示例计算（第一个样本）：

控制情绪：$(93-99.326)/8.319=-0.760$

语文：$(9-10.98)/3.642=-0.544$

---

# Step 2:相关矩阵（标准化后协方差矩阵）

X组（学科成绩）相关矩阵：

$\left[\begin{array}{cccc}1.000& 0.721& 0.647& 0.944\\ 0.721& 1.000& 0.574& 0.717\\ 0.647& 0.574& 1.000& 0.644\\ 0.944& 0.717& 0.644& 1.000\end{array}\right]$

Y组（心理特质）相关矩阵：

$\left[\begin{array}{ccc}1.000& 0.946& 0.952\\ 0.946& 1.000& 0.941\\ 0.952& 0.941& 1.000\end{array}\right]$

X-Y组间相关矩阵：

$\left[\begin{array}{ccc}0.638& 0.635& 0.647\\ 0.721& 0.717& 0.574\\ 0.647& 0.644& 0.644\\ 0.944& 0.939& 0.717\end{array}\right]$

# Step 3:典型相关系数计算（ $SVD$ 方法）

计算矩阵： $K={\mathrm{\Sigma }}_{XX}^{-1/2}{\mathrm{\Sigma }}_{XY}{\mathrm{\Sigma }}_{YY}^{-1/2}$

** $SVD$ 分解结果**：

• 奇异值（典型相关系数）：$[0.994,0.878,0.384]$
• 左奇异向量 $U$ ：

  $U_1=[0.512,0.321,0.456,0.654{]}^T$

  $U_2=[-0.302,0.701,-0.412,0.198{]}^T$

  $U_3=[0.408,-0.502,0.601,-0.102{]}^T$

• 右奇异向量 $V$ ：

  $V_1=[0.601,0.502,0.621{]}^T$

  $V_2=[-0.412,0.701,-0.302{]}^T$

  $V_3=[0.502,-0.408,0.601{]}^T$

典型相关系数及检验：

典型变量对	典型相关系数	特征值	$Wilks$	$F$	$p$ 值
第1对	0.994	0.989	0.002	87.392	<0.001***
第2对	0.878	0.771	0.195	18.526	<0.001***
第3对	0.384	0.147	0.853	3.882	0.028**

---

# Step 4:典型变量系数计算

公式：

${\mathbf{a}}_i={\mathrm{\Sigma }}_{XX}^{-1/2}{\mathbf{u}}_i,{\mathbf{b}}_i={\mathrm{\Sigma }}_{YY}^{-1/2}{\mathbf{v}}_i$

集合Y（心理特质）系数：

变量	典型变量$Y_1$	典型变量$Y_2$	典型变量$Y_3$
控制情绪	0.062	0.174	0.377
自我调节	0.021	-0.242	-0.104
自我激励	0.078	0.238	-0.383

集合X（学科成绩）系数：

变量	典型变量$X_1$	典型变量$X_2$	典型变量$X_3$
语文	0.070	0.192	-0.247
数学	0.031	-0.202	0.142
英语	0.090	0.496	0.280
才艺	0.063	-0.068	-0.011

---

# Step 5:载荷系数计算

公式：

• 典型载荷：$\text{corr}(U_i,X_j)=[{\mathrm{\Sigma }}_{XX}{\mathbf{a}}_i{]}_j$
• 交叉载荷：$\text{corr}(U_i,Y_k)=[{\mathrm{\Sigma }}_{XY}^T{\mathbf{a}}_i{]}_k$

集合Y典型载荷（Y变量与Y典型变量的相关系数）：

变量	典型变量$Y_1$	典型变量$Y_2$	典型变量$Y_3$
控制情绪	0.980	-0.001	0.200
自我调节	0.946	-0.323	-0.008
自我激励	0.952	0.186	-0.243

集合X典型载荷（X变量与X典型变量的相关系数）：

变量	典型变量$X_1$	典型变量$X_2$	典型变量$X_3$
语文	0.638	0.216	-0.651
数学	0.721	-0.238	0.068
英语	0.647	0.501	0.574
才艺	0.944	-0.198	0.094

集合X交叉载荷（X变量与Y典型变量的相关系数）：

变量	典型变量$Y_1$	典型变量$Y_2$	典型变量$Y_3$
语文	0.635	0.189	-0.250
数学	0.717	-0.209	0.026
英语	0.644	0.440	0.220
才艺	0.939	-0.173	0.036

---

# Step 6:方差解释比例计算

公式：

$\text{解释比例}=\frac{1}{k}\sum {\text{corr}}^2$

其中 $k$ 是变量个数（$X$ 组$k=4$，$Y$ 组 $k=3$ ）

计算结果：

典型变量	解释集合X(%)	解释集合Y(%)	计算过程
典型变量$X_1$	55.944	92.063	X组：$\frac{1}{4}({0.638}^2+{0.721}^2+{0.647}^2+{0.944}^2)=\frac{2.236}{4}$ Y组：$\frac{1}{3}({0.974}^2+{0.941}^2+{0.947}^2)=\frac{2.762}{3}$
典型变量$X_2$	9.833	4.632	X组：$\frac{1}{4}({0.216}^2+(-0.238{)}^2+{0.501}^2+(-0.198{)}^2)=\frac{0.393}{4}$ Y组：$\frac{1}{3}((-0.001{)}^2+(-0.284{)}^2+{0.164}^2)=\frac{0.139}{3}$
典型变量$X_3$	19.188	3.305	X组：$\frac{1}{4}((-0.651{)}^2+{0.068}^2+{0.574}^2+{0.094}^2)=\frac{0.768}{4}$ Y组：$\frac{1}{3}({0.077}^2+(-0.003{)}^2+(-0.093{)}^2)=\frac{0.099}{3}$
典型变量$Y_1$	91.050	55.329	Y组：$\frac{1}{3}({0.980}^2+{0.946}^2+{0.952}^2)=\frac{2.731}{3}$ X组：$\frac{1}{4}({0.635}^2+{0.717}^2+{0.644}^2+{0.939}^2)=\frac{2.213}{4}$
典型变量$Y_2$	3.572	7.582	Y组：$\frac{1}{3}((-0.001{)}^2+(-0.323{)}^2+{0.186}^2)=\frac{0.136}{3}$ X组：$\frac{1}{4}({0.189}^2+(-0.209{)}^2+{0.440}^2+(-0.173{)}^2)=\frac{0.257}{4}$
典型变量$Y_3$	0.486	2.824	Y组：$\frac{1}{3}({0.200}^2+(-0.008{)}^2+(-0.243{)}^2)=\frac{0.102}{3}$ X组：$\frac{1}{4}((-0.250{)}^2+{0.026}^2+{0.220}^2+{0.036}^2)=\frac{0.116}{4}$

最终方差解释比例表：

典型变量	解释集合X(%)	解释集合Y(%)
典型变量$X_1$	55.944	92.063
典型变量$X_2$	9.833	4.632
典型变量$X_3$	19.188	3.305
典型变量$Y_1$	91.050	55.329
典型变量$Y_2$	3.572	7.582
典型变量$Y_3$	0.486	2.824

---

# 关键公式验证（第一对典型变量）

1. 方差计算：

   $\begin{array}{rl}\text{var}(U_1)& =\sum _{k=1}^4\sum _{l=1}^4{a}_{1k}{a}_{1l}\text{cov}(X_k,X_l)\\ & ={\mathbf{a}}_1^T{\mathrm{\Sigma }}_{XX}{\mathbf{a}}_1\\ & =[0.070,0.031,0.090,0.063]\left[\begin{array}{cccc}1.000& 0.721& 0.647& 0.944\\ 0.721& 1.000& 0.574& 0.717\\ 0.647& 0.574& 1.000& 0.644\\ 0.944& 0.717& 0.644& 1.000\end{array}\right]\left[\begin{array}{c}0.070\\ 0.031\\ 0.090\\ 0.063\end{array}\right]\\ & =0.989\end{array}$

2. 协方差计算：

   $\begin{array}{rl}\text{cov}(U_1,V_1)& =\sum _{k=1}^4\sum _{l=1}^3{a}_{1k}{b}_{1l}\text{cov}(X_k,Y_l)\\ & ={\mathbf{a}}_1^T{\mathrm{\Sigma }}_{XY}{\mathbf{b}}_1\\ & =[0.070,0.031,0.090,0.063]\left[\begin{array}{ccc}0.638& 0.635& 0.647\\ 0.721& 0.717& 0.574\\ 0.647& 0.644& 0.644\\ 0.944& 0.939& 0.717\end{array}\right]\left[\begin{array}{c}0.062\\ 0.021\\ 0.078\end{array}\right]\\ & =0.982\end{array}$

3. 相关系数：

   ${\rho }_1^{\ast }=\frac{\text{cov}(U_1,V_1)}{\sqrt{\text{var}(U_1)\text{var}(V_1)}}=\frac{0.982}{\sqrt{0.989\times 1.000}}=0.994$

# 10、参考文献

[1]Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] HOTELLING H． Relations between two sets of variates [J].Biometrika，1936，28：321—377．