线性判别

操作视频

# 1、作用

线性判别的原理是将样本投影到一条直线上，使得同类样本的投影点尽可能接近，不同样本的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的直线上，再根据投影点的位置来确定新样本的类别。其中线性判别(LDA)也常用于数据降维，可在数据处理的降维部分使用。

# 2、输入输出描述

输入：自变量X为1个或1个以上的定量变量，因变量Y为一个定类变量。
输出：模型的分类结果和模型分类的评价效果。

# 3、案例示例

示例：根据红酒的颜色强度，脯氨酸，类黄酮等变量，生成一个能够区分琴酒，雪莉，贝尔摩德三种品种的红酒的线性判别模型。

# 4、案例数据

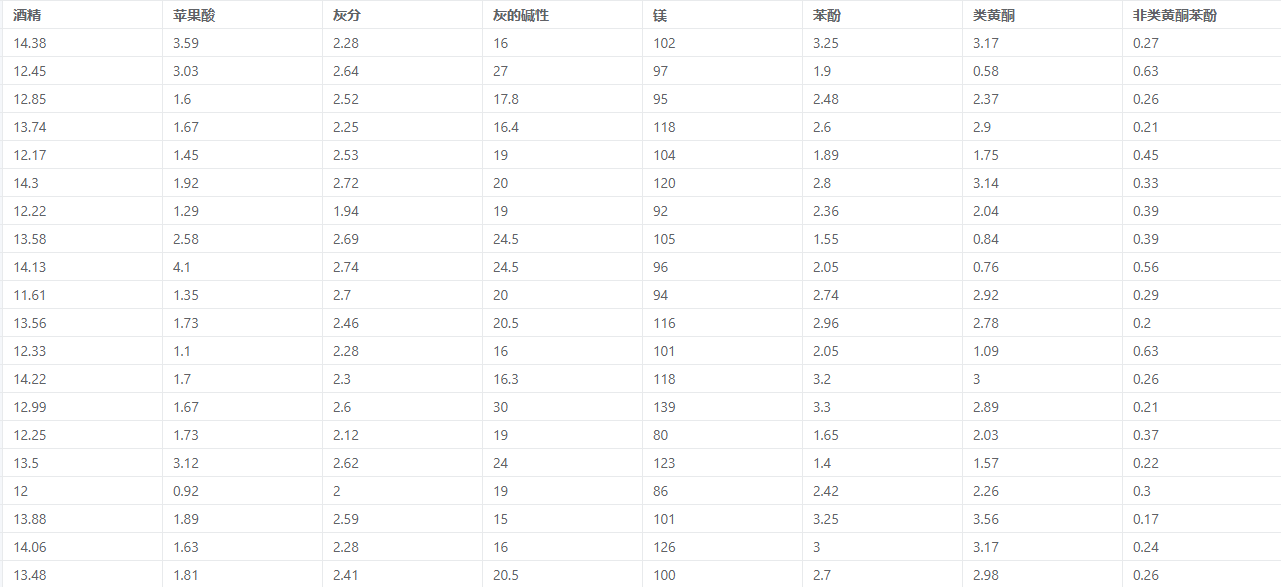
判别分析案例数据

# 5、案例操作

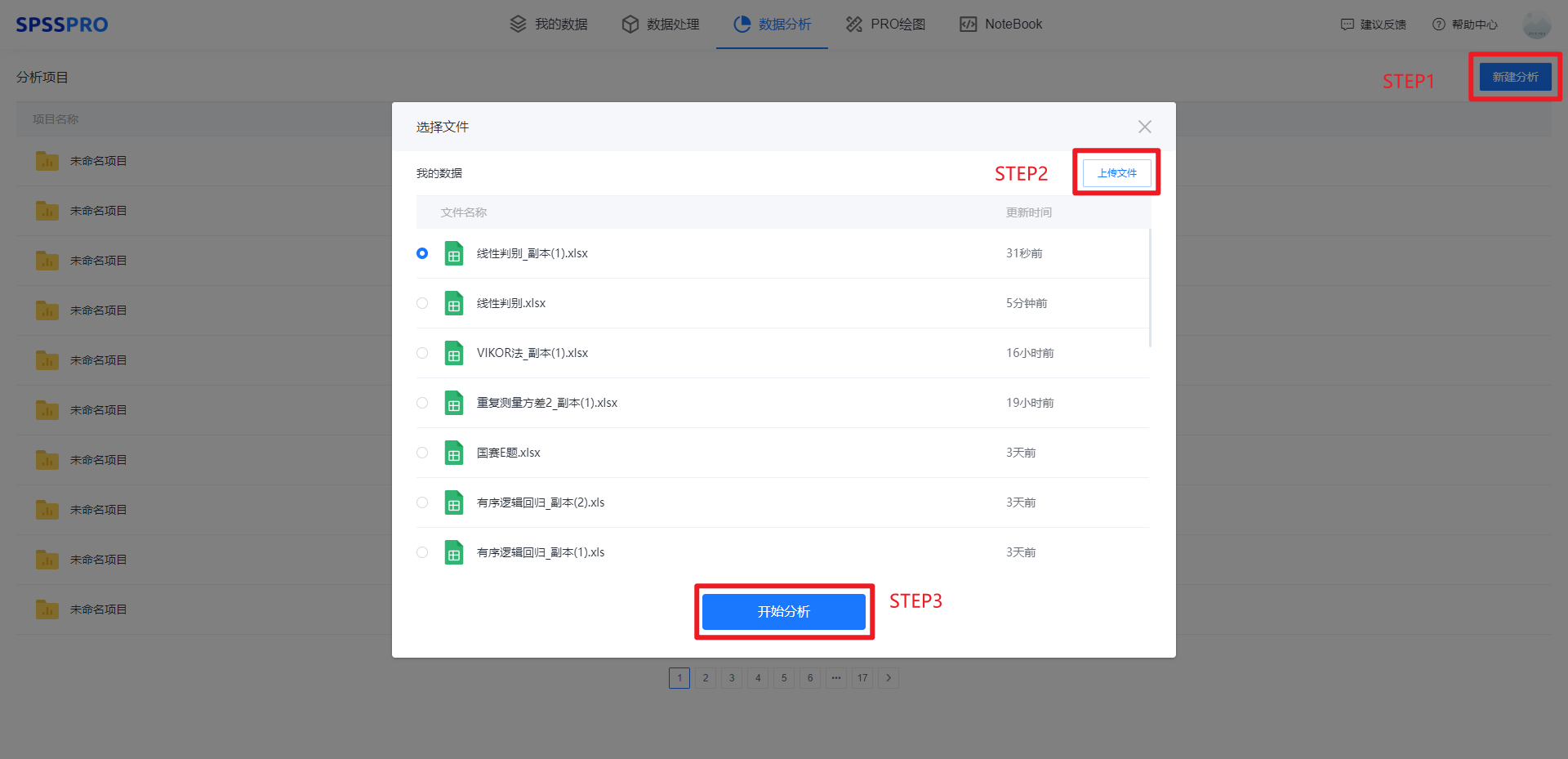
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；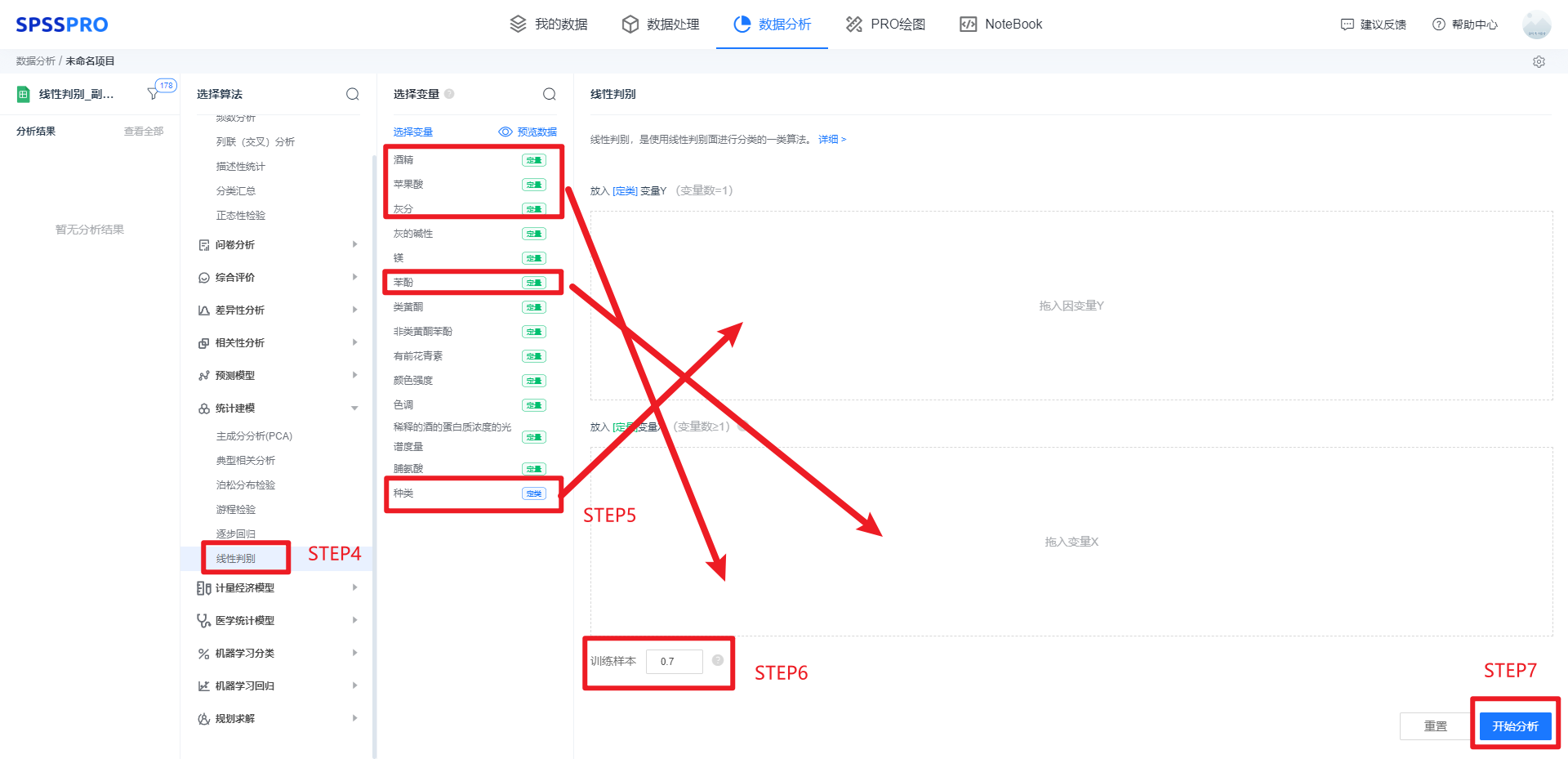

step4：选择【判别分析】；
step5：查看对应的数据数据格式，按要求输入【判别分析】数据;
step6：选择训练样本的比例，本例为默认0.7;
step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果1：判别函数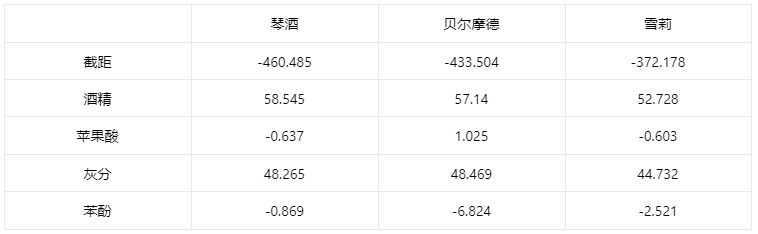

图表说明：
上表展示了线性判别的判别函数，可以将数据代入其中，然后比较不同类别的判别函数值大小进行分类，最大的值即为被判断的种类。
智能分析：
模型的判别函数如下：
琴酒=-460.485 + 58.545×酒精 - 0.637×苹果酸 + 48.265×灰分 - 0.869×苯酚
贝尔摩德=-433.504 + 57.14×酒精 + 1.025×苹果酸 + 48.469×灰分 - 6.824×苯酚
雪莉=-372.178 + 52.728×酒精 - 0.603×苹果酸 + 44.732×灰分 - 2.521×苯酚
分析：
可以将新的样本代入判别函数进行计算，用于对新样本进行类别判断。

输出结果2：混淆矩阵热力图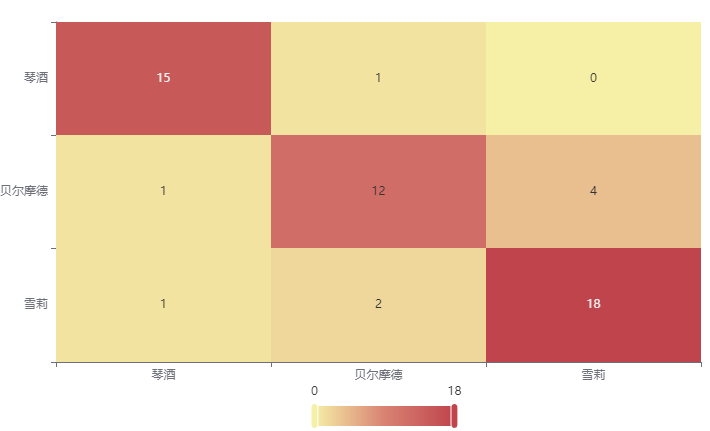

图表说明：
上表以热力图的形式展示了混淆矩阵。

输出结果3：模型评估结果
图表说明：
上表中展示了训练集和测试集的预测评价指标，通过量化指标来衡量线性判别的预测效果。 ● 准确率：预测正确样本占总样本的比例，准确率越大越好。
● 召回率：实际为正样本的结果中，预测为正样本的比例，召回率越大越好。
● 精确率：预测出来为正样本的结果中，实际为正样本的比例，精确率越大越好。
● F1：精确率和召回率的调和平均，精确率和召回率是互相影响的，虽然两者都高是一种期望的理想情况，然而实际中常常是精确率高、召回率就低，或者召回率低、但精确率高。若需要兼顾两者，那么就可以用F1指标。

输出结果4：测试数据预测评估结果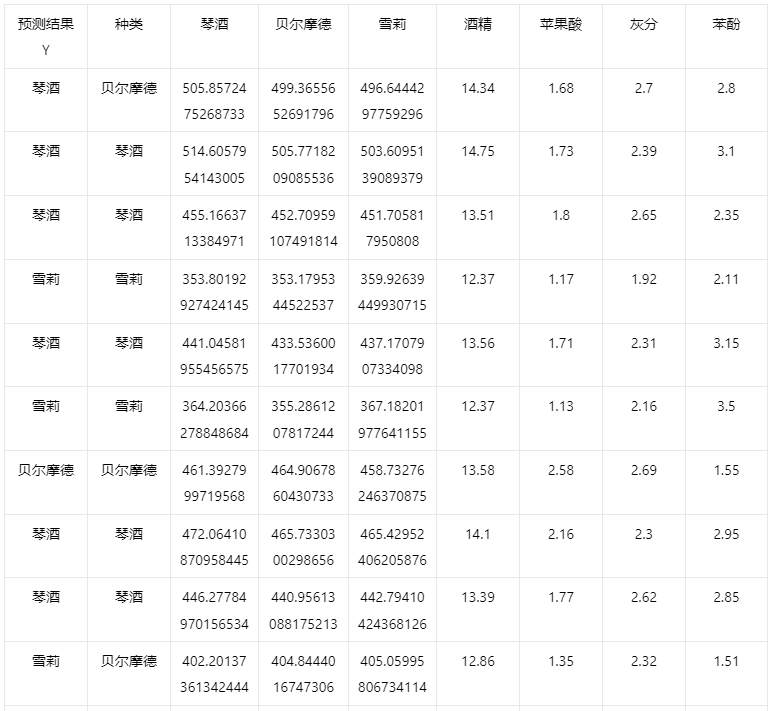

图表说明：
上表格为预览结果，只显示部分数据，全部数据请点击下载按钮导出。
上表展示了线性判别对测试数据的分类结果，分类结果值是拥有最大判别函数计算值的分类组别。

# 7、注意事项

对于本判别分析模型而言，二分类与多分类的计算方法并不一致。
本判别分析模型使用的为Fisher判别法。

# 8、模型理论

# 基本原理

本判别分析使用的判别算法为Fisher判别法，其基本原理如下：
为了克服由于维数高而引起的“维数灾难”，就需要将高维数据点投影到低维空间（如一维直线）上，从而使得数据点更为密集，这就是费歇判别法的基本思想，下文分别解释二分类和多分类的判别分析情况。

# 二分类情况

判别函数：
假设有两个总体 $G_{1}$ ， $G_{2}$ 分别从两总体中独立抽取 $n_{1}$ , $n_{2}$ 个p维训练样本。两类样本的平均值为：
$\overset{―}{X_{p}^{(k)}} = (x_{1}^{i}, . . ., x_{p}^{i})^{T} (p = 1, 2, . . ., m; i = 1, 2, . . ., n_{k}; k = 1, 2)$

两类样本的协方差阵 $S_{k}$ :
$S_{k} = \frac{1}{n_{k} - 1} \sum_{t = 1}^{n_{k}} (X_{(t)}^{(k)} - X^{(k)}) (X_{(t)}^{(k)} - X^{(k)})^{T}, (k = 1, 2)$

当两个总体的协差阵 $\sum_{1}^{}$ , $\sum_{2}^{}$ 等于总协差阵 $\sum_{}^{}$ 时，协差阵 $\sum_{}^{}$ 的无偏估计即为总样本的协差阵S:
$S = \frac{(n_{1} - 1) S_{1} + (n_{2} - 1) S_{2}}{n_{1} + n_{2} - 2}$

假设新建立的判别式为:
$y = \sum_{i = 1}^{p} c_{i} x_{i}$

想要使判别函数能够最佳的体现出来自不同总体样本的区别，可构造函数：
$d_{p} = \overset{―}{X_{p}^{(1)}} - \overset{―}{X_{p}^{(2)}}$
$s_{p j} = \sum_{i = 1}^{n_{j}} (x_{i n}^{(t)} - \overset{―}{X_{p}^{(1)}}) < b r / > (x_{i j}^{(1)} - \overset{―}{X_{j}^{(1)}}) + \sum_{i = 1}^{n_{2}} (x_{i p}^{(2)} - \overset{―}{X_{p}^{(2)}}) < b r / > (x_{i j}^{(2)} - \overset{―}{X_{j}^{(2)}})$

由此可确定判别函数的系数 $c_{1}, c_{2}, . . ., c_{p}$ ，即：
$[\begin{matrix} c_{1} \\ c_{2} \\ . . . \\ c_{p} \end{matrix}] = S^{- 1} [\begin{matrix} x_{1}^{(1)} - x_{1}^{(2)} \\ x_{2}^{(1)} - x_{2}^{(2)} \\ . . . \\ x_{p}^{(1)} - x_{p}^{(2)} \end{matrix}]$

从而得到新的判别函数:
${\begin{matrix} s_{11} c_{1} + s_{12} c_{2} + . . . + s_{1 p} c_{p} = d_{1} \\ s_{21} c_{1} + s_{22} c_{2} + . . . + s_{2 p} c_{p} = d_{2} \\ . . . . . . . . . . . . . . . . . . . . . . . . . . . . \\ s_{p 1} c_{1} + s_{p 2} c_{2} + . . . + s_{p p} c_{p} = d_{p} \end{matrix}$

得到判别函数后，确定判别临界值 $y_{0}$ 。如果二总体具有共同的先验概率，通常令 $y_{0}$ 是
${\overset{―}{y}}^{(1)}$ 与 ${\overset{―}{y}}^{(2)}$ 的加权平均值，也就是：
$y_{0} = \frac{n_{1} {\overset{―}{y}}^{(1)} + n_{2} {\overset{―}{y}}^{(2)}}{n_{1} + n_{2}}$ ，其中 ${\overset{―}{y}}^{(1)} = \sum_{k = 1}^{p} c_{k} {\overset{―}{x_{k}}}^{(1)}$ ，\overline{y}^{(2)} = \sum_{k=1}^{p}c_k \overline{x_k}^{(2)}.

判别准则：
现有一个观测数据 $X = (x_{1}, . . ., x_{p})^{T}$ 套用判别函数，解得结果值y。
当 ${\overset{―}{y}}^{(1)} > {\overset{―}{y}}^{(2)}$ ,如果y> $y_{0}$ 那么判断X属于 $G_{1}$ ;
当 ${\overset{―}{y}}^{(1)} > {\overset{―}{y}}^{(2)}$ ,如果y< $y_{0}$ 那么判断X属于 $G_{2}$ ;
当 ${\overset{―}{y}}^{(1)} < {\overset{―}{y}}^{(2)}$ ,如果y> $y_{0}$ 那么判断X属于 $G_{2}$ ;
当 ${\overset{―}{y}}^{(1)} < {\overset{―}{y}}^{(2)}$ ,如果y< $y_{0}$ 那么判断X属于 $G_{1}$ 。

# 多分类情况

判别函数：
设有k个总体 $G_{1}, . . ., G_{k}$ ，抽取样品数分别为 $n_{1}, n_{2}, . . ., n_{k}$ ，令 $n = n_{1} + n_{2} + . . . + n_{k}$ ， $X_{α}^{(i)} = (X_{α 1}^{(i)}, . . ., X_{α p}^{(i)})$ 为第i个总体的第α个样品的观测向量。

假定所建立的判别函数为：
有 $y (x) = c_{1} x_{1} + . . . + c_{p} x_{p} Δ_{=}^{b} c^{'} x$
y(x)在 $G_{i}$ 上的样本均值与样本方差为 ${\overset{―}{y}}^{(i)} = c^{'} {\overset{―}{x}}^{(i)}$ ， $σ_{i}^{2} = c^{'} {\overset{―}{s}}^{(i)} c$ 。这里 ${\overset{―}{x}}^{(i)}$ ， ${\overset{―}{s}}^{(i)}$ 依次为 $G_{i}$ 内x的样本均值向量和样本协差阵。
要选取系数向量c，即需使 $λ = \frac{\sum_{j = 1}^{k} n_{i} ({\overset{―}{y}}^{(i)} - \overset{―}{y})^{2}}{\sum_{i = 1}^{k} q_{i} σ_{i}^{2}}$ 达到最大。这里 $q_{i}$ 为自己设定的正的加权系数，通常取作先验概率。令 $q_{i} = n_{i} - 1$ ，计算可得：
$λ = \frac{c^{'} A c}{c^{'} E c}$ ,其中 $E = \sum_{i = 1}^{k} q_{i} s^{(i)}$ 为组内离差阵， $A = \sum_{i = 1}^{k} n_{i} ({\bar{x}}^{(i)} - \bar{x}) ({\bar{x}}^{(i)} - \bar{x})^{'}$ 为总体直接样本协差阵。可得模型如下：
$m a x = c^{'} A c / c^{'} E c$
并需要使其最大。

可构造m个判别函数：
$y_{t} (x) = c^{(l)^{'}} x, l = 1, . . ., m$

用 $λ_{1}, λ_{2}, . . ., λ_{m} (λ_{1} \geq λ_{2} \geq . . . \geq λ_{m} \geq 0)$ 表示全部非零特征根， $l_{1}, l_{2}, . . ., l_{m}$ 为相应的特征向量。当 $α = l_{1}$ 时，可使 $△ (α)$ 达到极大。

判别准则：
假设把总体分成p个类，若 $| \begin{matrix} y_{p} - {\bar{y}}_{1} \end{matrix} | < | \begin{matrix} y_{p} - {\bar{y}}_{q} \end{matrix} | (p, q = 1, 2, . . ., m . q \neq 1)$ ，则 $y_{p}$ 属于第1类。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 陈华豪.介绍判别分析——一种多元分析工具[J].林业勘查设计,1981(04):49-52.
[3] 赵丽娜. Fisher判别法的研究及应用[D]. 东北林业大学, 2013.

建议反馈