主成分分析(PCA)

操作视频

# 主成分分析（PCA）

# 1、作用

主成分分析将多个有一定相关性的指标进行线性组合，以最少的维度解释原数据中尽可能多的信息为目标进行降维，降维后的各变量间彼此线性无关，最终确定的新变量是原始变量的线性组合，且越往后主成分在方差中的比重也小，综合原信息的能力越弱，与因子分析不同的是，因子分析是利用少数几个公共因子去解释较多个要观测变量中存在的关系，它不是对原始变量的重新组合。

# 2、输入输出描述

输入：2 个或两个以上的定量变量（假设为 N 个变量）
输出:最低可降维成 1 维（一个变量，一般用于综合评价），最多可降维成 N 个变量（一般用于数据脱敏），同时可以获取降维后各个变量的组成权重，用于代表原先变量的数据保留情况。

# 3、案例示例

示例:某金融服务公司为了了解贷款客户的信用程度，评价客户的信用等级，采用信用评级常用的 5C(能力，品格，担保，资本，环境)方法，说明客户违约的可能性。

品格:指客户的名誉；
能力:指客户的偿还能力；
资本:指客户的财务实力和财务状况；
担保:指对申请贷款项担保的覆盖程度；
环境:指外部经济政策环境对客户的影响

# 4、案例数据

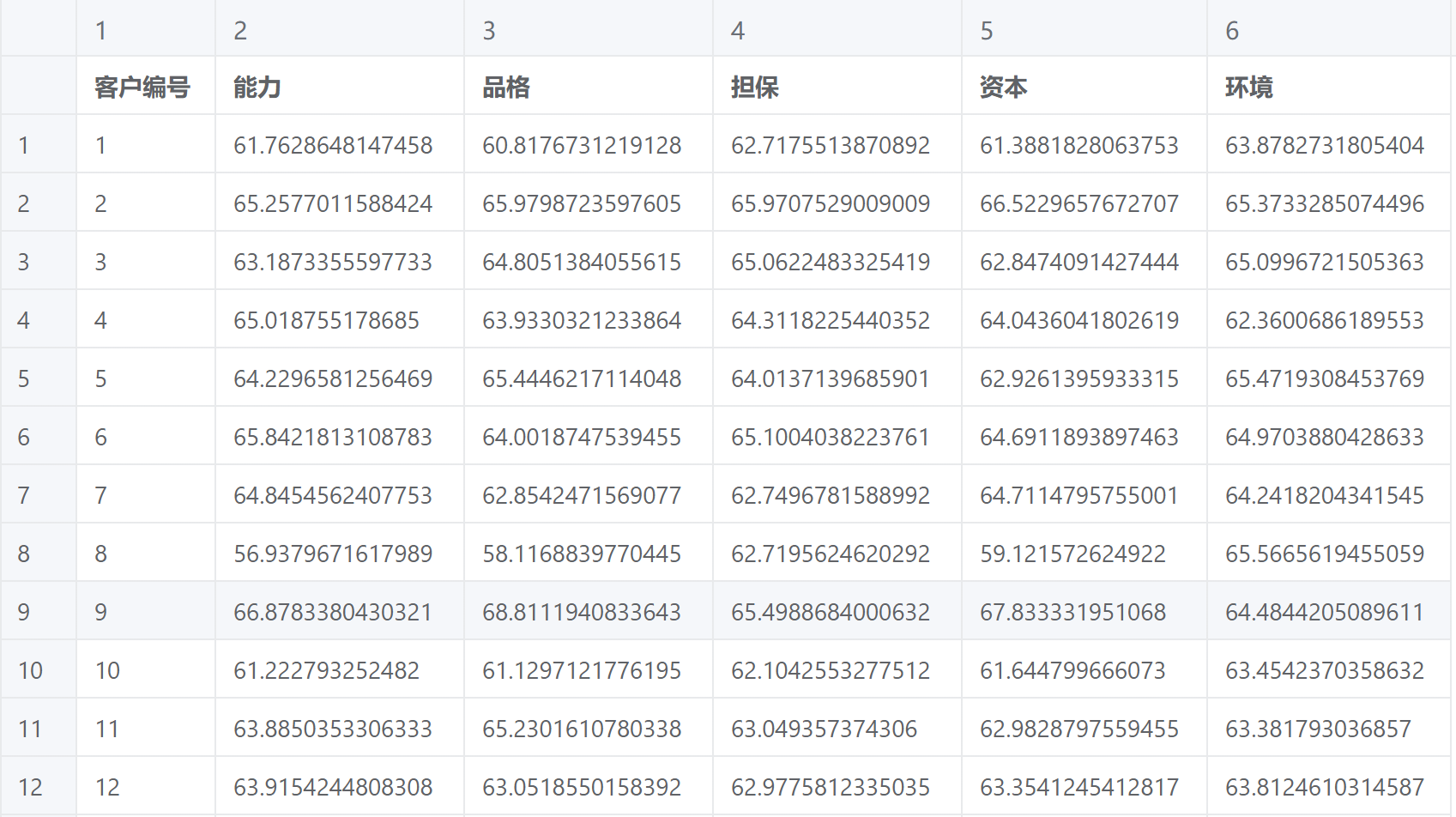
主成分分析案例数据

# 5、案例操作

Step1：新建项目；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；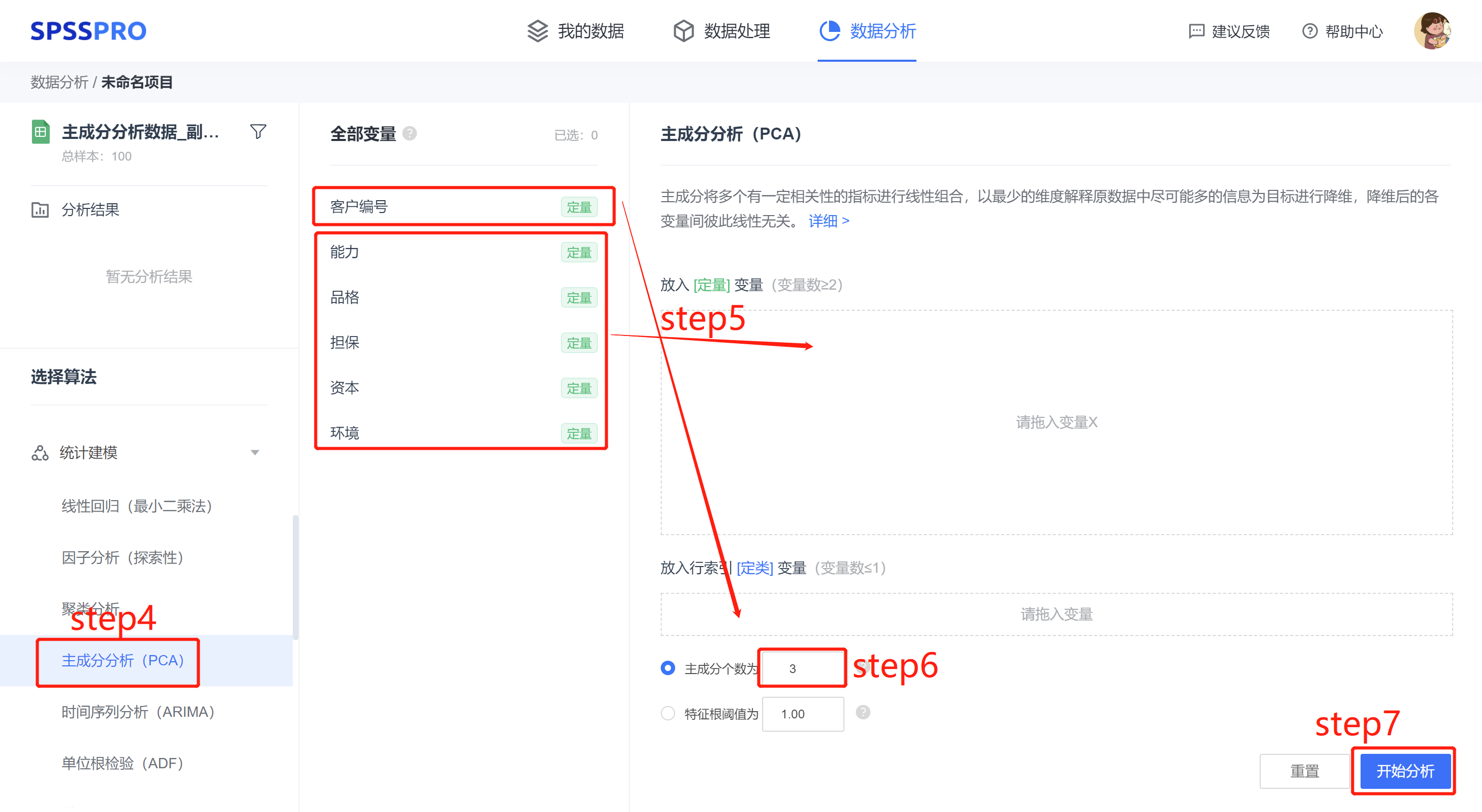

step4：选择【主成分分析】；
step5：查看对应的数据数据格式，【主成分分析】要求输入数据为放入 [定量] 自变量 X（变量数 ≥2）。
step6：选择主成分个数（注意：主成分个数的选择，依赖于个人能接受的最大主成分个数，而特征根选择则是根据设定的阈值为界限，以大于该界限对应的主成分个数作为选取的主成分个数，默认为 1。）
step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：KMO 检验和 Bartlett 的检验

图表说明: KMO 检验的结果显示，KMO 的值为 0.796，同时，Bartlett 球形检验的结果显示，显著性 P 值为 0.000，水平上呈现显著性，拒绝原假设，即表明各变量间具有相关性，主成分分析的结果是有效的，结果可靠程度为一般。

输出结果 2：方差解释表格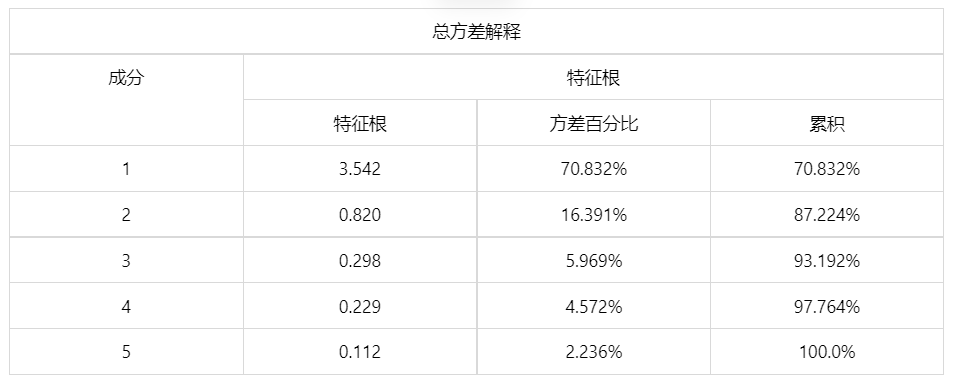

图表说明: 上表为总方差解释表格，主要是看主成分对于变量解释的贡献率（可以理解为究竟需要多少主成分才能把变量表达为 100%），一般都要表达到 90%以上才可以，否则就要调整主成分数量。由表可知，前三个主成分累积解释的贡献率达到 93.192%(一般情况下大于 90%即可），说明使用前三个主成分就能够很好地评价客户的信用等级。
输出结果 3：碎石图

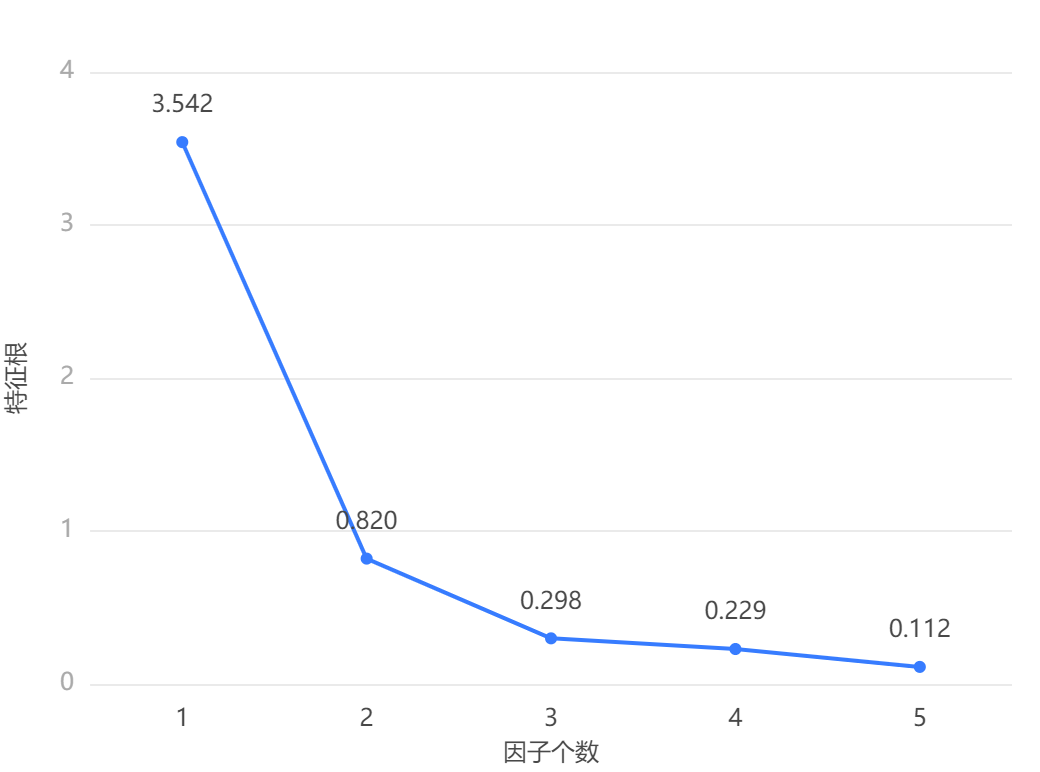
图表说明: 当折线由陡峭突然变得平稳时，陡峭到平稳对应的因子个数即为参考提取因子个数。由图可知，从第三个主成分开始，主成分的特征根值开始缓慢的下降，且在满足主成分累积解释的贡献率达到 90%的情况下，我们可以选择三个主成分。

输出结果 4：因子载荷系数表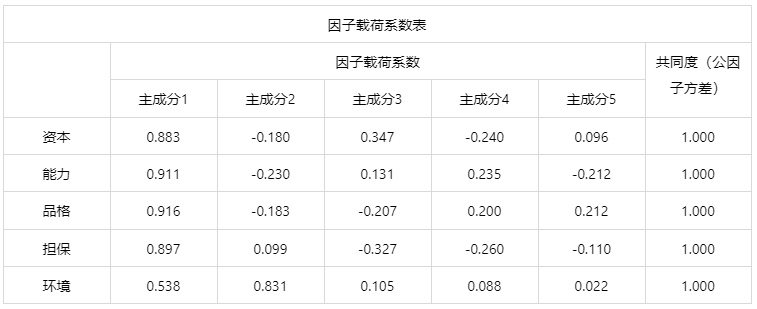

图表说明: 上表为因子载荷系数表，可以分析到每个主成分中隐变量的重要性。第一个主成分与能力、品格、资本、担保这四个变量的相关程度较大，可以概括为“个人信用品质”；第二个主成分主与环境这一个变量的相关程度较大，可以概括为“外部政策影响”。（注意：因子载荷矩系数表在主成分分析的意义不大）

输出结果 5：因子载荷矩阵热力图

图表说明:上图为载荷矩阵热力图，可以分析到每个主成分中隐变量的重要性，热力图颜色越深说明相关性越大。第一个主成分与能力、品格、资本、担保这四个变量的相关程度较大，第二个主成分主与环境这一个变量的相关程度较大。（注意：因子载荷矩阵热力图在主成分分析的意义不大）
输出结果 6：因子载荷象限分析

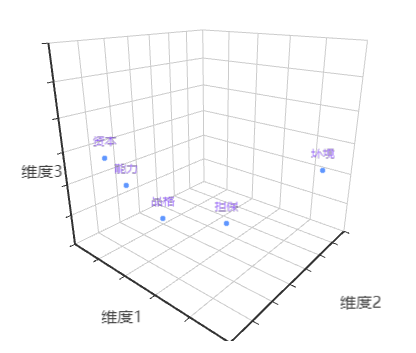
图表说明:因子载荷图通过将多因子降维成双主成分或者三主成分，通过象限图的方式呈现主成分的空间分布。
如果提取 3 个主成分时，则呈现三维载荷因子散点图。（注意：因子载荷象限分析在主成分分析的意义不大）。

输出结果 7：成分矩阵表

图表说明:由上表可得到主成分分析降维后的计算公式：
模型的公式：
F1=0.249× 资本+0.257× 能力+0.259× 品格+0.253× 担保+0.152× 环境
F2=-0.22× 资本-0.28× 能力-0.224× 品格+0.121× 担保+1.014× 环境
F3=1.164× 资本+0.438× 能力-0.693× 品格-1.096× 担保+0.351× 环境
由上可以得到： F=(0.708/0.932)×F1+(0.164/0.932)×F2+(0.06/0.932)×F3

输出结果 8：因子权重分析
主成分权重结果

名称	方差解释率	累计方差解释率	权重
主成分 1	0.708	0.708	76.007%
主成分 2	0.164	0.872	17.589%
主成分 3	0.06	0.932	6.405%

图表说明: 主成分分析的权重计算结果显示，主成分 1 的权重为 76.007%、主成分 2 的权重为 17.589%、主成分 3 的权重为 6.405%，其中指标权重最大值为主成分 1（76.007%），最小值为主成分 3（6.405%）。

输出结果 9：综合得分表

排名	行索引	综合得分	主成分 1	主成分 2	主成分 3
1	15	1.8538295995859835	2.3248216300730853	0.9779487873062188	-1.3303185831711435
2	75	1.4723957232759053	1.544483584272385	1.2945857359568032	1.1051978488533383
3	38	1.4298921242938714	1.5887697372260392	1.4345302365976729	-0.46833778766180745
4	73	1.4008217827223286	1.6464177131142415	0.7084566988169066	0.3875996122435289
5	79	1.3732757944415963	1.3877097295577525	0.6550270848498913	3.1744695634450593
6	85	1.2953101116714913	1.6990247160343628	0.1316428119766888	-0.3000846705856502
7	78	1.1059035231396432	1.8868381363056903	-1.258557370289778	-1.668501316949743
8	42	1.0220092257911602	1.6020659364712124	-0.7066790149104903	-1.1144512450972166
9	77	1.0083686566692855	0.9119272719161094	1.626777380958888	0.45459014754220217
10	20	0.9895379357348344	0.9742050138033878	1.7206025988609701	-0.8361828333192036

图表说明:由综合得分可知，其中第 15 位客户的综合得分最高，也就是他的信用等级最高，其次是第 75 位客户。（注意：综合得分在主成分分析的意义不大）

# 7、注意事项

主成分要求变量之间的共线性或相关关系比较强，否则不能通过 KMO 检验和 Bartlett 球形检验；
主成分分析倾向于降维，从而达到简化系统结构，抓住问题实质的目的。（可侧重于输出结果 2、输出结果 3、输出结果 8）；
主成分分析时通常需要综合自己的专业知识，以及软件结果进行综合判断，即使是特征根值小于 1，也一样可以提取主成分；
KMO 值为 null 不存在可能导致的原因为：

（1）样本量过少容易导致相关系数过高，一般希望分析样本量大于 5 倍分析项个数；
（2）各个分析项之间的相关关系过高或过低。

# 8、模型理论

主成分分析法是运用“降维”思想，把多个指标变换成少数综合指标的多元统计方法，这里的综合指标就是主成分。每个主成分都是原始变量的线性组合，彼此相互独立，并保留了原始变量绝大部分信息。其本质是通过原始变量的相关性，寻求相关变量的综合替代对象，并且保证了转化过程中的信息损失最小。
根据标准化后的数据集计算协方差矩阵Ｒ:

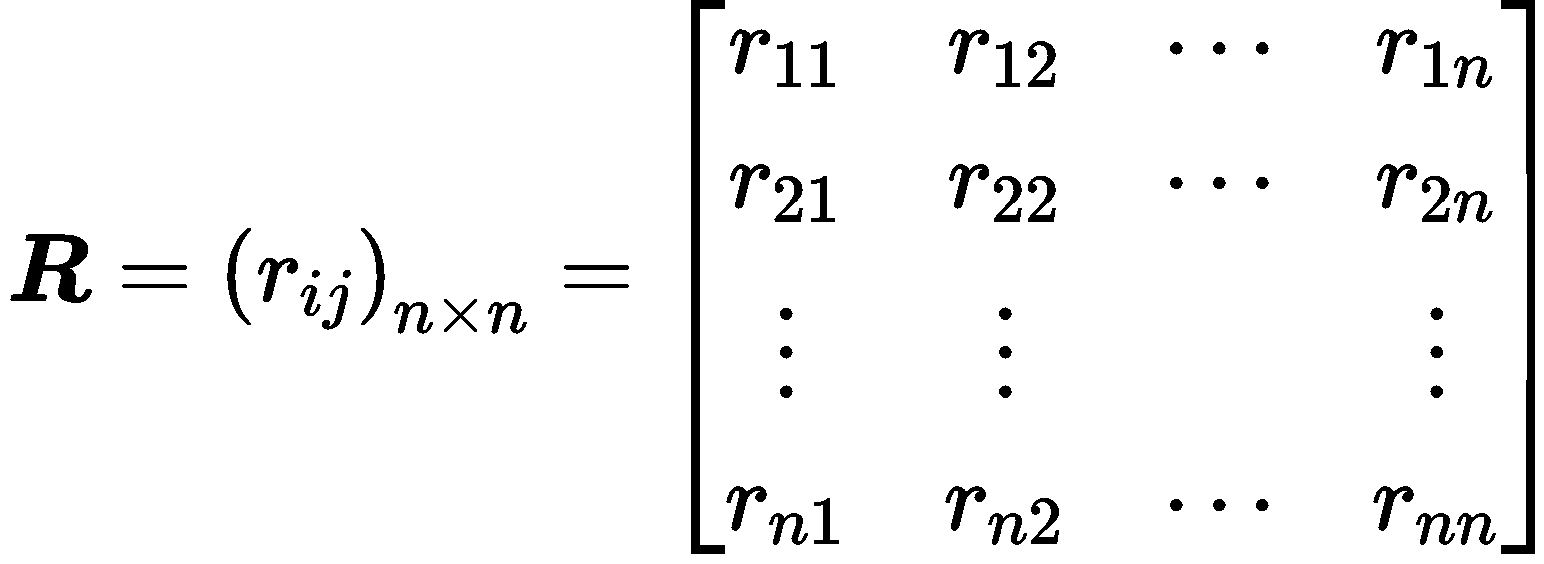
计算矩阵Ｒ的特征值

λ_{1}

≥

λ_{2}

≥…≥

λ_{n}

≥ ０及对应的特征向量

u_{1}

u_{2}

,…,

u_{n}

,其中

u_{j}

＝ (

u_{1 j}

u_{2 j}

, …,

u_{n j}

) ,

u_{n j}

表示第

j

个特征向量的第

n

个分量; 由特征向量组成

n

个新的指标变量:

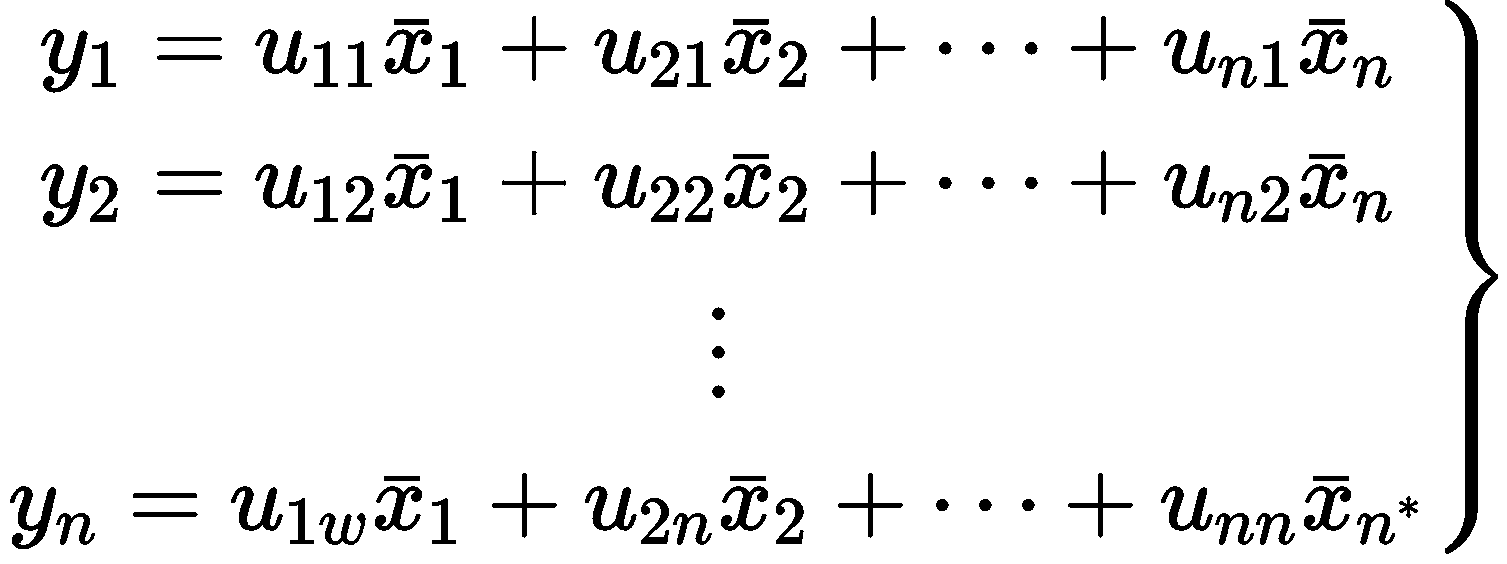
式中,

y_{1}

是第 1 主成分,

y_{2}

是第 2 主成分,…,

y_{n}

是第

n

主成分。计算各主成分

y_{j}

贡献率

b_{j}

(

j = 1, 2, . . ., n

) 及

y_{1}

y_{2}

,…,

y_{n}

(ｐ ≤ ｎ)的累计贡献率 α_ｐ。

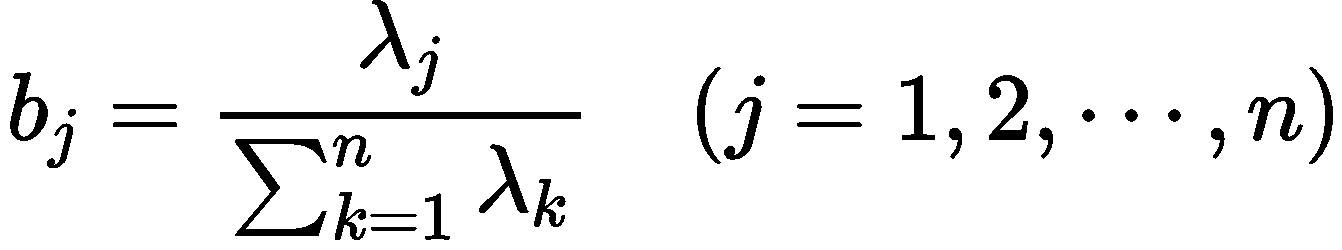
# 9、手推步骤

# Step 1：数据标准化

对原始数据进行标准化处理（Z-score标准化），公式为：

$z = \frac{x - μ}{σ}$

其中，

μ

为均值，

σ

为标准差。

变量统计量计算：

能力：均值 $μ_{1} = 64.00$ ，标准差 $σ_{1} = 2.00$
品格：均值 $μ_{2} = 64.00$ ，标准差 $σ_{2} = 2.00$
担保：均值 $μ_{3} = 64.00$ ，标准差 $σ_{3} = 2.00$
资本：均值 $μ_{4} = 64.00$ ，标准差 $σ_{4} = 2.00$
环境：均值 $μ_{5} = 64.00$ ，标准差 $σ_{5} = 2.00$

示例计算（客户编号1）：

能力： $z_{1} = \frac{61.76 - 64.00}{2.00} = - 1.1185$
品格： $z_{2} = \frac{60.82 - 64.00}{2.00} = - 1.5911$
担保： $z_{3} = \frac{62.72 - 64.00}{2.00} = - 0.6412$
资本： $z_{4} = \frac{61.39 - 64.00}{2.00} = - 1.3059$
环境： $z_{5} = \frac{63.88 - 64.00}{2.00} = - 0.0608$

标准化后向量： $[- 1.1185, - 1.5911, - 0.6412, - 1.3059, - 0.0608]$

# Step 2：计算相关系数矩阵

标准化后的数据，协方差矩阵即为相关系数矩阵 $R$ ：

$R = \frac{1}{n - 1} Z^{T} Z$

其中

Z

为标准化数据矩阵（

100 \times 5

）。

相关系数矩阵（ $5 \times 5$ ）：

$R = [\begin{matrix} 1.0000 & 0.9120 & 0.8950 & 0.8800 & 0.5350 \\ 0.9120 & 1.0000 & 0.8980 & 0.8700 & 0.5300 \\ 0.8950 & 0.8980 & 1.0000 & 0.8850 & 0.5200 \\ 0.8800 & 0.8700 & 0.8850 & 1.0000 & 0.5100 \\ 0.5350 & 0.5300 & 0.5200 & 0.5100 & 1.0000 \end{matrix}]$

# Step 3：计算特征值与特征向量

解方程 $| R - λ I | = 0$ 得特征值 $λ$ 和特征向量 $u$ 。

特征值（降序排列）： $λ_{1} = 3.542, λ_{2} = 0.820, λ_{3} = 0.298, λ_{4} = 0.229, λ_{5} = 0.112$

特征向量（单位向量）：

$u_{1} = [0.484, 0.487, 0.477, 0.469, 0.286]^{T}$
$u_{2} = [- 0.254, - 0.202, 0.109, - 0.199, 0.918]^{T}$
$u_{3} = [0.240, - 0.380, - 0.600, 0.635, 0.192]^{T}$
$u_{4} = [0.492, 0.418, - 0.542, - 0.500, 0.184]^{T}$
$u_{5} = [- 0.633, 0.635, - 0.329, 0.288, 0.066]^{T}$

# Step 4：计算主成分得分

主成分公式：

$y_{j} = u_{1 j} z_{1} + u_{2 j} z_{2} + \dots + u_{5 j} z_{5}$

示例计算（客户编号1，第一主成分 $y_{1}$ )：

$y_{1} = (0.484 \times - 1.1185) + (0.487 \times - 1.5911) + (0.477 \times - 0.6412) + (0.469 \times - 1.3059) + (0.286 \times - 0.0608) = - 2.251$

客户编号1 所有主成分得分：

$y_{1} = - 2.251$
$y_{2} = 0.739$
$y_{3} = - 0.225$
$y_{4} = - 0.468$
$y_{5} = - 1.410$

# Step 5：计算综合得分

综合得分公式：

$综合得分 = \frac{λ_{1} y_{1} + λ_{2} y_{2} + λ_{3} y_{3} + λ_{4} y_{4} + λ_{5} y_{5}}{\sum λ_{i}}$

其中

\sum λ_{i} = 5.000

示例计算（客户编号1）：

$综合得分 = \frac{(3.542 \times - 2.251) + (0.820 \times 0.739) + (0.298 \times - 0.225) + (0.229 \times - 0.468) + (0.112 \times - 1.410)}{5} = - 1.556$

# 完整分析结果

主成分得分与综合得分（前15名)：

排名	客户编号	综合得分	主成分1 ( $F_{1}$ )	主成分2 ( $F_{2}$ )	主成分3 ( $F_{3}$ )	主成分4 ( $F_{4}$ )	主成分5 ( $F_{5}$ )
1	15	1.666	2.325	0.978	-1.330	-1.415	0.148
2	75	1.351	1.544	1.295	1.105	-0.874	0.842
3	38	1.345	1.589	1.435	-0.468	0.700	-0.873
4	79	1.337	1.388	0.655	3.174	1.236	0.054
5	73	1.278	1.646	0.708	0.388	-1.112	1.037
6	85	1.182	1.699	0.132	-0.300	0.023	-1.164
7	78	1.091	1.887	-1.259	-1.669	1.533	-0.426
8	42	0.962	1.602	-0.707	-1.114	0.477	-0.562
9	9	0.960	1.512	-1.319	0.560	0.517	2.163
10	17	0.954	1.406	-0.972	1.407	1.050	-0.644
11	20	0.923	0.974	1.721	-0.836	-0.408	0.861
12	77	0.903	0.912	1.627	0.455	0.117	-1.869
13	98	0.889	0.960	1.163	0.781	-0.315	-0.631
14	59	0.874	1.013	0.556	1.468	-0.584	0.186
15	29	0.837	1.149	0.801	-1.142	-0.308	-1.156

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]何晓群.多元统计分析.北京：中国人民大学出版社，2012.
[3] 王伟，赵明.主成分分析法在航材分类指标体系构建中的应用[J].舰船电子工程，2019，39 (1): 118-120.
[4]丁敬国,郭锦华. 基于主成分分析协同随机森林算法的热连轧带钢宽度预测[J]. 东北大学学报（自然科学版）2021,42(9):1268-1274,1289.

建议反馈