拟合工具箱
# 拟合工具箱
# 1、作用
拟合工具箱是处理一个变量或者两个变量的拟合问题,适用于对二维、三维数据的进行线性、非线性拟合。
# 2、输入输出描述
输入:因变量为一个定量变量;自变量为不超过 2 个的定量变量。
输出:拟合效果以及可视化拟合情况。
# 3、案例示例
案例:现当前有一组数据,两个 x,一个 y,根据拟合工具箱对自变量和因变量的关系进行分析。
# 4、案例数据

拟合工具箱案例数据
# 5、案例操作
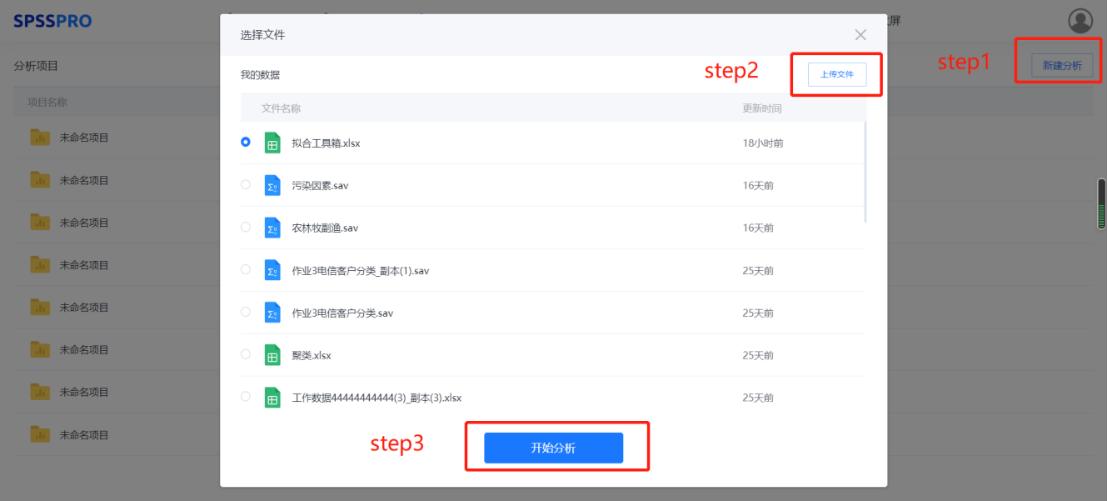
Step1:新建分析;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;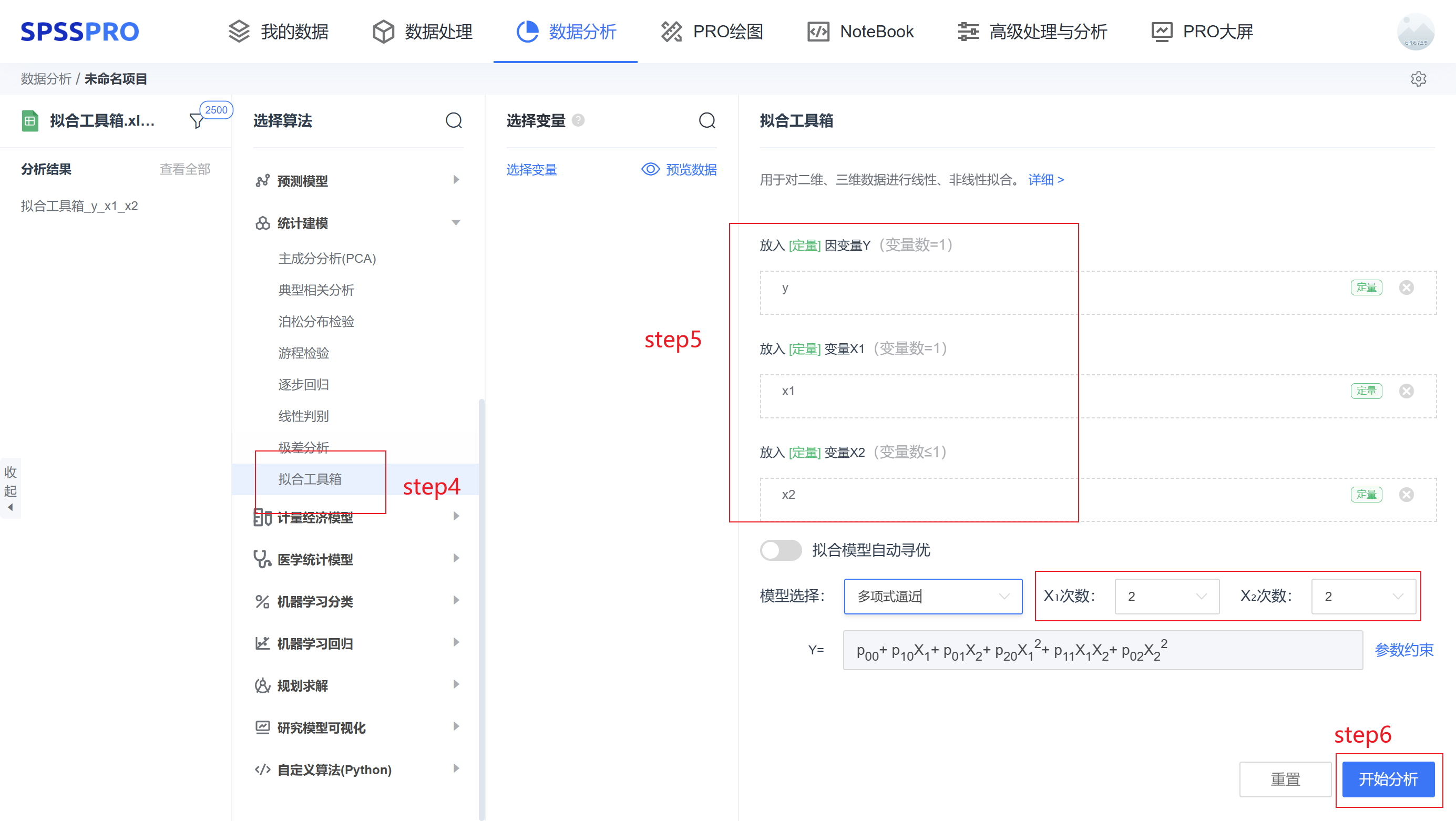
step4:选择【拟合工具箱】;
step5:查看对应的数据数据格式,【拟合工具箱】要求因变量为一个定量变量;自变量为不超过 2 个的定量变量。
step6:点击【开始分析】,完成全部操作。
# 6、输出结果分析
输出结果 1:拟合评价表
| R² | RMSE |
|---|---|
| 1 | 7.275351235944175e-9 |
图表说明:
上表展示了模型的拟合评价指标结果。
● R² :多重测定系数,该值越接近 1,表明方程的变量对 y 的解释能力越强。
● RMSE:均方根误差,该值越接近 0 的值表示误差较小、预测较好。
上表中的 R 方等于 1,均方根误差趋近于 0,说明完美拟合,模型拟合结果优秀。
输出结果 2:拟合结果表
| 参数 | 估计值 | 95%置信上限 | 95%置信下限 |
|---|---|---|---|
| p00 | 0 | 0 | 0 |
| p10 | 0 | 0 | 0 |
| p01 | 0 | 0 | 0 |
| p20 | 1 | 1 | 1 |
| p11 | 0 | 0 | 0 |
| p02 | 1 | 1 | 1 |
图表说明:上表展示了模型的拟合结果,包括各个参数的估计结果以及估计置信上限、下限(表明参数有 95%的可能性落在[置信上限,置信下限]的区间),由估计值可以得到模型的公式。
智能分析:模型的公式为:Y = -0.0+-0.0x1+0.0x2+1.0x1^2+0.0x1x2+1.0x2^2。
输出结果 3:拟合效果图
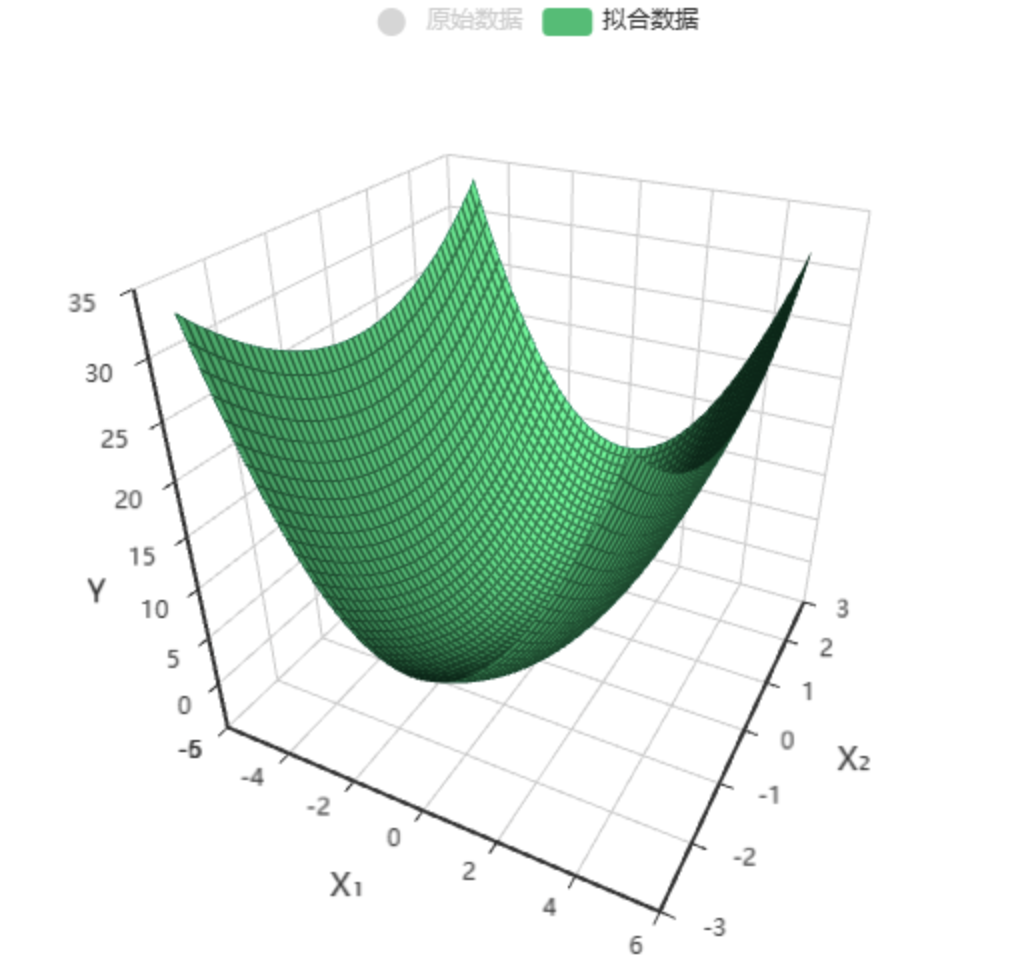
图表说明:左图是原始散点图,右图是拟合曲面效果图,原始散点图都接近与拟合曲线或是拟合曲面,说明拟合效果较好。
# 7、注意事项
- 无
# 8、模型理论
(一)对于一个自变量的拟合,可选择的方法有
多项式逼近、指数逼近、傅里叶逼近、高斯逼近、幂逼近、正弦曲线逼近、威布尔逼近、有理数逼近
- 多项式逼近: 多项式逼近是使用一个多项式函数来拟合数据。多项式函数是一组常数项和幂次项的和。通过选择适当的多项式次数,我们可以根据数据点的分布获得较好的拟合效果。多项式逼近通常使用最小二乘法来确定多项式系数,以使多项式与数据点的误差最小化。
- 指数逼近: 指数逼近是使用指数函数来拟合数据。指数函数具有形式 y = a * e^(bx),其中 a 和 b 是拟合参数。这种逼近适用于数据的增长或衰减遵循指数规律的情况。
- 傅里叶逼近: 傅里叶逼近是使用三角函数(正弦和余弦函数)的线性组合来拟合数据。它是傅里叶级数的近似,可以将任意周期函数分解为多个正弦和余弦函数的和。通过使用适当数量的三角函数项,可以逼近许多周期性函数。
- 高斯逼近: 高斯逼近使用高斯函数(或称为正态分布)来拟合数据。高斯函数具有钟形曲线,可用于拟合数据的分布情况。
- 幂逼近: 幂逼近是使用幂函数来拟合数据。幂函数具有形式 y = ax^b,其中 a 和 b 是拟合参数。幂逼近适用于某些数据具有幂律关系的情况,例如幂律分布。
- 正弦曲线逼近: 正弦曲线逼近是使用正弦函数来拟合数据。正弦函数具有周期性,适用于周期性数据。
- 威布尔逼近: 威布尔逼近使用威布尔分布函数来拟合数据。威布尔分布函数是一种广泛应用于可靠性工程和生存分析的概率分布函数。
- 有理数逼近: 有理数逼近是使用有理函数(多项式之比)来拟合数据。有理函数可以表示为 y = (p(x) / q(x)),其中 p(x)和 q(x)是两个多项式函数。这种逼近方法适用于某些数据具有有理函数关系的情况。
(二)对于两个自变量的拟合,可选择的方法有
多项式逼近:两个自变量的多项式逼近原理与一维情况类似,但涉及到两个自变量
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 周纪芗. 实用回归分析方法[M]. 上海科学技术出版社, 1990.
