对数线性模型

操作视频

SPSSPRO教程-对数线性模型

# 对数线性模型

# 1、作用

对数线性模型用于处理多个分类变量的关系，通过估计各个变量水平及交互水平的系数来检验各变量及其交互效应的作用大小；卡方分析只能通过列联表分析两个分类变量，对于多个分类变量无能为力，由此建议使用对数线性模型。

# 2、输入输出描述

输入：一个或多个的定类变量以及可选的协变量。
输出：预测频数和实际频数的差异以及各个变量水平对频数的影响。

# 3、案例示例

案例：某公司的员工的基本信息：学历、文科理科、收入水平，使用对数线性模型对这三个变量的关系进行分析。

# 4、案例数据

对数线性模型案例数据

# 5、案例操作

Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；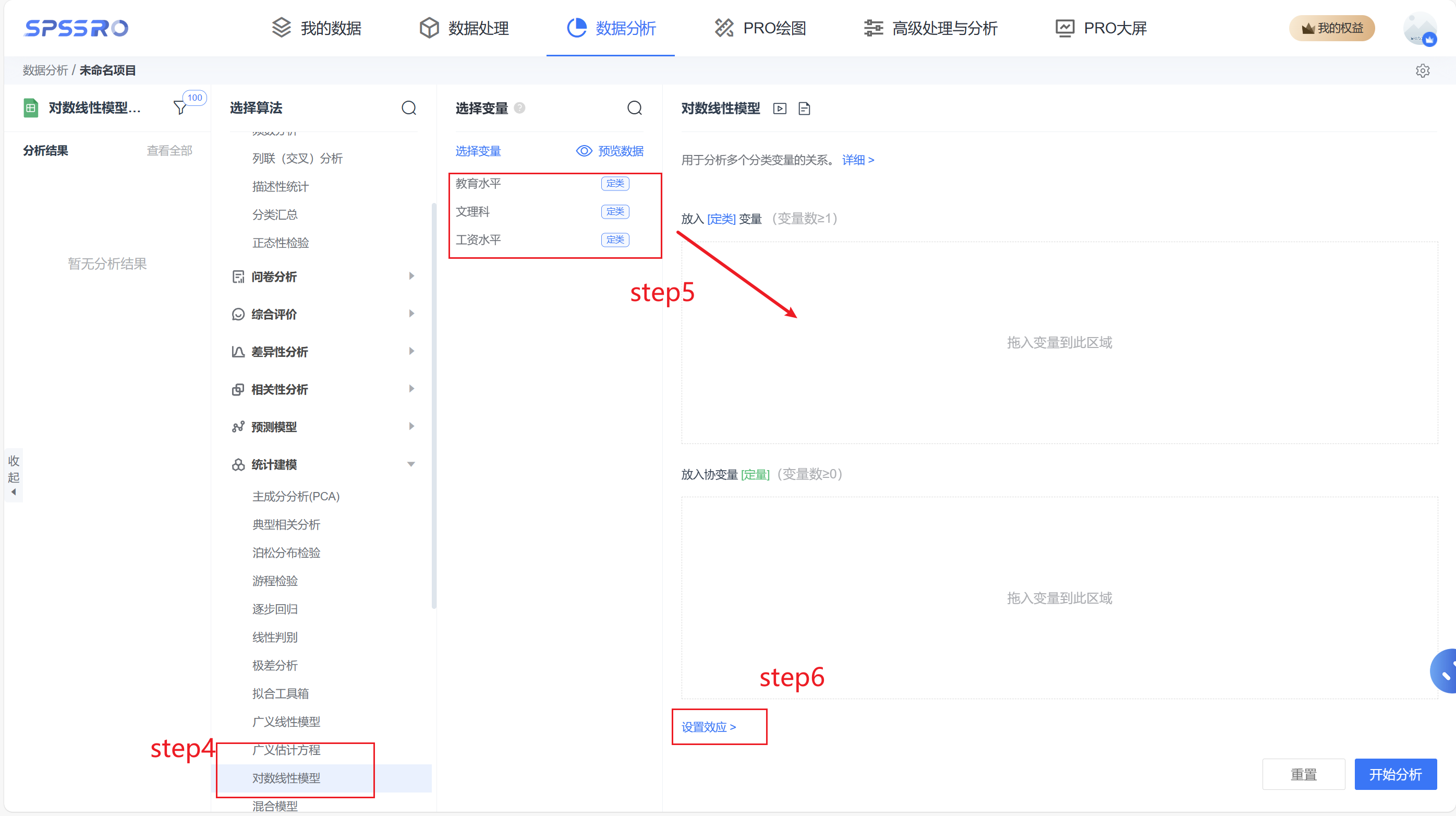

step4：选择【对数线性模型】；
step5：查看对应的数据数据格式，按照【对数线性模型】要求拖入变量；
step6：设置主效应和交互项；
step7：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果1：拟合优度检验

	值	自由度	P
似然比	13.606	11	0.256
皮尔逊卡方	10.839	11	0.457

图表说明：上表展示了拟合优度检验结果。
● 若当检验结果P≥0.05时，说明模型拟合较好，数据预测频数接近观测频数，结果准确性强。
● 但如果检验结果P<0.05，就说明模型拟合程度不好，提示应适当调整模型，重新进行对数线性分析。
以上结果拟合优度检验P=0.256，不呈现显著性，说明模型拟合较好，数据预测频数接近观测频数。

输出结果2：效应值估计

图表说明：上表展示了各个水平的效应值。效应值代表水平对因变量的频数的影响系数；

输出结果3：实际统计与期望统计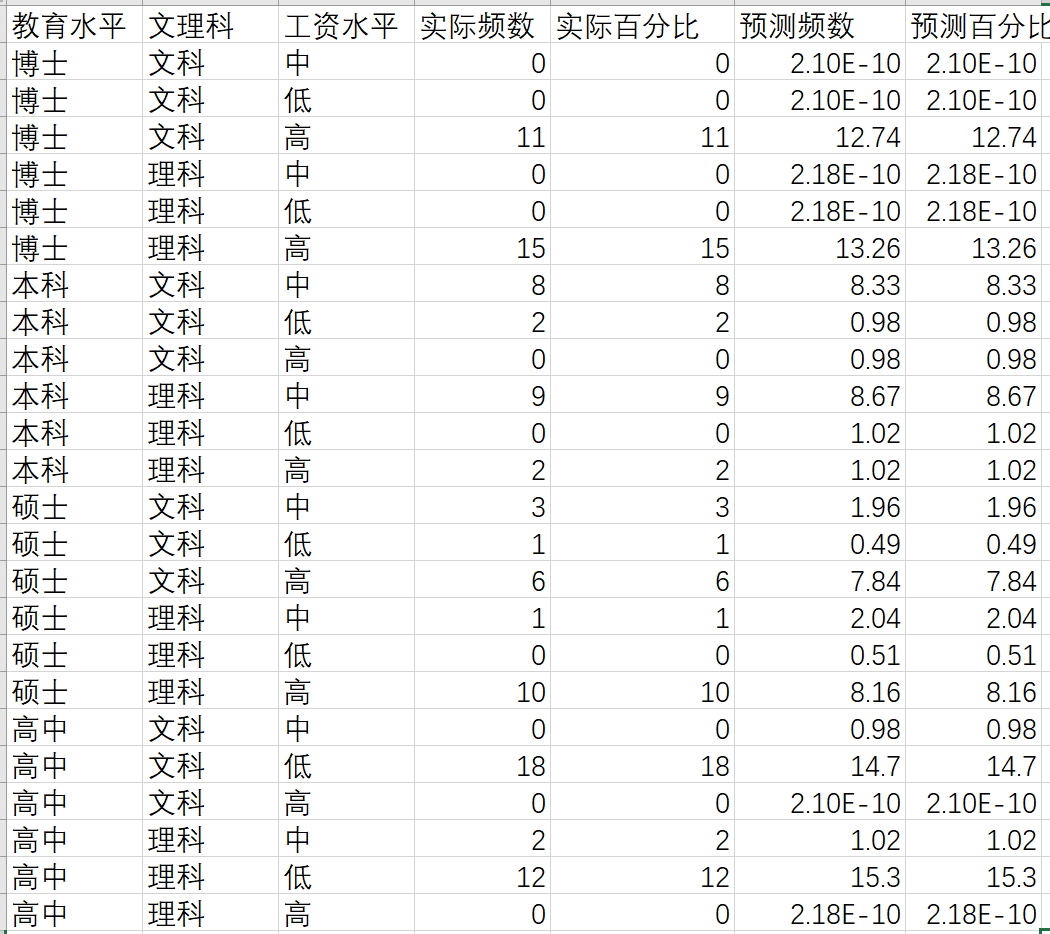

图表说明：上表展示了各个分类变量水平组合的实际频数、预测频数及其占总样本例数的比例，实际频数与预测频数越接近，说明该模型拟合得越好。

# 7、注意事项

输出结果2效应值估计可能会缺少分类水平，这是由于模型中涉及到泊松回归模型，待分析项作为定类自变量，会按照哑变量进行处理，n个分类水平会有（n-1）个哑变量；比如学历：小学、初中、高中、本科，处理之后会有1个水平作为基准项，最终只保留三个分类水平。

# 8、模型理论

对数线性模型是线性模型的一种扩展形式，它采用了对数函数来建模因变量的期望和自变量之间的关系。其形式如下：

其中，λi 是第 i 个观测的期望计数。这个数值需要对分类变量进行频数统计，然后将频数作为因变量，待分析变量为自变量建立泊松回归模型。
模型的参数_β_0,_β_1,…,βk 可以通过最大似然估计等方法估计得到，它们的解释与普通线性模型相似，表示因变量对自变量的影响。

# 9、手推步骤

教育水平	文理科	工资水平
硕士	文科	高
硕士	文科	高
高中	理科	低
高中	文科	低
本科	理科	中
高中	理科	低
高中	文科	低
高中	文科	低
硕士	理科	高
本科	理科	中

对数线性模型求解过程如下：

step1：交叉频数表
数据表中包含三个变量：教育水平、文理科和工资水平，列出所有可能的组合以及出现的次数，完整频数表如下：

编号	教育水平	文理科	工资水平	频数 y
1	高中	理科	低	2
2	高中	文科	低	3
3	高中	理科	中	0
4	高中	文科	中	0
5	高中	理科	高	0
6	高中	文科	高	0
7	本科	理科	低	0
8	本科	文科	低	0
9	本科	理科	中	2
10	本科	文科	中	0
11	本科	理科	高	0
12	本科	文科	高	0
13	硕士	理科	低	0
14	硕士	文科	低	0
15	硕士	理科	中	0
16	硕士	文科	中	0
17	硕士	理科	高	1
18	硕士	文科	高	2

step2：设置哑变量
教育水平：
$E_{1} = 1$ 如果教育水平=本科，否则 $E_{1} = 0$
$E_{2} = 1$ 如果教育水平=硕士，否则 $E_{2} = 0$
基准：高中（E1=0,E2=0）
文理科：
W = 1 如果文理科=文科，否则W = 0
基准：理科（W=0）
工资水平：
$S_{1} = 1$ 如果工资水平=中，否则 $S_{1} = 0$
$S_{2} = 1$ 如果工资水平=低，否则 $S_{2} = 0$
基准：高（S1=0,S2=0）
则有对数线性模型：

\log (λ) = β_{0} + β_{1} E_{1} + β_{2} E_{2} + β_{3} W + β_{4} S_{1} + β_{5} S_{2}

step3：求解系数
对于三维列联表，对数线性模型（独立模型）的期望频数公式是

{\hat{λ}}_{a b c} = n \cdot \frac{y_{a + +}}{n} \cdot \frac{y_{+ b +}}{n} \cdot \frac{y_{+ + c}}{n} = \frac{y_{a + +} \cdot y_{+ b +} \cdot y_{+ + c}}{n^{2}}

取自然对数后有

\ln {\hat{λ}}_{a b c} = \ln y_{a + +} + \ln y_{+ b +} + \ln y_{+ + c} - 2 \ln n

{高中，本科，硕士}={1，2，3}，{理科，文科}={1，2}，{低，中，高}={1，2，3}
基准组（高中，理科，高）：
$y_{1 + +} = 5, y_{+ 1 +} = 5, y_{+ + 3} = 3, n = 10$
$\ln {\hat{λ}}_{1, 1, 3} = \ln 5 + \ln 5 + \ln 3 - 2 \ln 10 \approx - 0.288$
所以 $β_{0} = - 0.288$
本科效应（教育水平=本科，其他=基准）：
$y_{2 + +} = 2, y_{+ 1 +} = 5, y_{+ + 3} = 3, n = 10$
$\ln {\hat{λ}}_{2, 1, 3} = \ln 2 + \ln 5 + \ln 3 - 2 \ln 10 \approx - 1.204$
与基准组的差： $- 1.204 - (- 0.288) = - 0.916$
所以 $β_{1} = - 0.916$
硕士效应（教育水平=硕士，其他=基准）：
$y_{3 + +} = 3, y_{+ 1 +} = 5, y_{+ + 3} = 3, n = 10$
$\ln {\hat{λ}}_{3, 1, 3} = \ln 3 + \ln 5 + \ln 3 - 2 \ln 10 \approx - 0.799$
与基准组的差： $- 0.799 - (- 0.288) = - 0.511$
所以 $β_{2} = - 0.511$
文科效应（文理科=文科，其他=基准）：
$y_{1 + +} = 5, y_{+ 2 +} = 5, y_{+ + 3} = 3, n = 10$
$\ln {\hat{λ}}_{1, 2, 3} = \ln 5 + \ln 5 + \ln 3 - 2 \ln 10 \approx - 0.288$
与基准组的差： $- 0.288 - (- 0.288) = 0$
所以 $β_{3} = 0$
中工资效应（工资水平=中，其他=基准）：
$y_{1 + +} = 5, y_{+ 1 +} = 5, y_{+ + 2} = 2, n = 10$
$\ln {\hat{λ}}_{1, 1, 3} = \ln 5 + \ln 5 + \ln 2 - 2 \ln 10 \approx - 0.693$
与基准组的差： $- 0.693 - (- 0.288) = - 0.405$
所以 $β_{4} = - 0.405$
低工资效应（工资水平=低，其他=基准）：
$y_{1 + +} = 5, y_{+ 1 +} = 5, y_{+ + 1} = 5, n = 10$
$\ln {\hat{λ}}_{1, 1, 3} = \ln 5 + \ln 5 + \ln 5 - 2 \ln 10 \approx 0.223$
与基准组的差： $0.223 - (- 0.288) = 0.511$
所以 $β_{5} = 0.511$
最终模型为 $\log (λ) = - 0.288 - 0.916 E_{1} - 0.511 E_{2} - 0.405 S_{1} + 0.511 S_{2}$ 。

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.

建议反馈