广义线性模型

操作视频

# 广义线性模型

# 1、作用

广义线性模型（GLM）是一种通用的模型，用于不同类型的数据和分布，包括二项分布（用于二分类问题）、泊松分布（用于计数数据）、正态分布等，且不一定要求因变量和自变量之间是线性关系；而线性回归OLS适用于因变量是连续的、正态分布的，且自变量对因变量的关系是线性的。

# 2、输入输出描述

输入：1个定量因变量；1个或以上的自变量。
输出：自变量对因变量的影响程度。

# 3、案例示例

案例：假设正在研究某种药物和不同年龄（不同年龄具有不同的免疫能力）这两个变量对患者的治疗效果。

# 4、案例数据

广义线性模型案例数据

# 5、案例操作

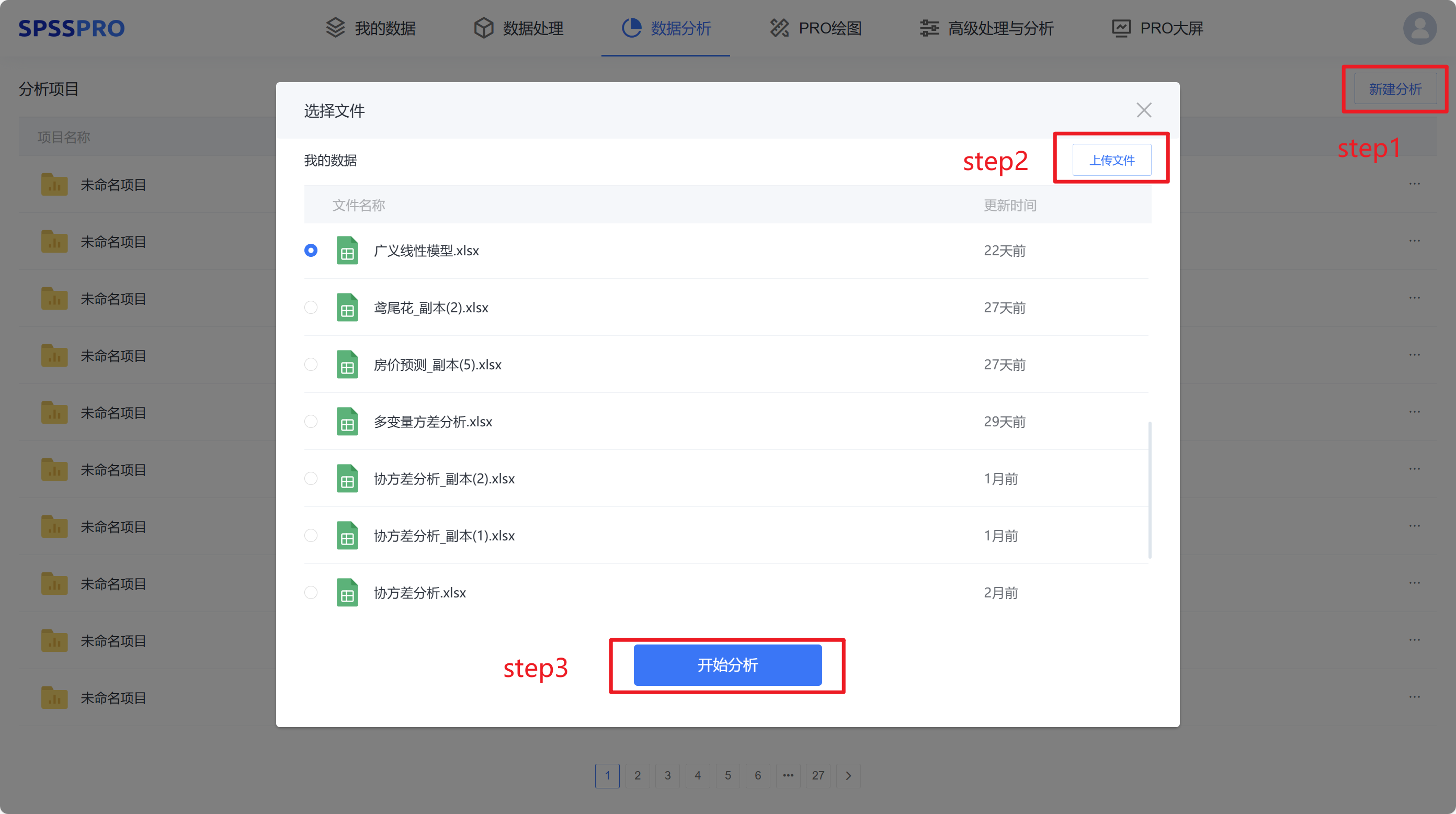
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

step4：选择【广义线性模型】；
step5：查看对应的数据数据格式，按照【广义线性模型】要求拖入变量
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果1：Omnibus检验

似然比卡方	自由度	P
202.25	3	0.000***

图表说明：上表展示了Omnibus检验结果，用于同时检验模型中的多个系数是否显著。若P<0.05，表明至少有一个自变量对因变量有显著影响，即整个模型显著。Omnibus检验结果显示，显著性𝑝值0.000***，水平上呈现显著性，至少有一个自变量对因变量有显著影响，因而模型是有效的。

输出结果2：参数估计表

参数	系数	标准误差	Wald	P	95%置信区间下限	95%置信区间上限
截距	67.421	6.791	98.561	0.000***	54.111	80.731
Age	2.906	0.175	275.643	0.000***	2.563	3.249
Treatment_A	1.791	3.861	0.215	0.643	-5.778	9.359
Treatment_B	5.216	3.841	1.844	0.174	-2.312	12.744

图表说明：上表展示了参数估计的结果。由上表可知，年龄对血压有显著影响，且年龄与血压成正比；

输出结果3：预测结果表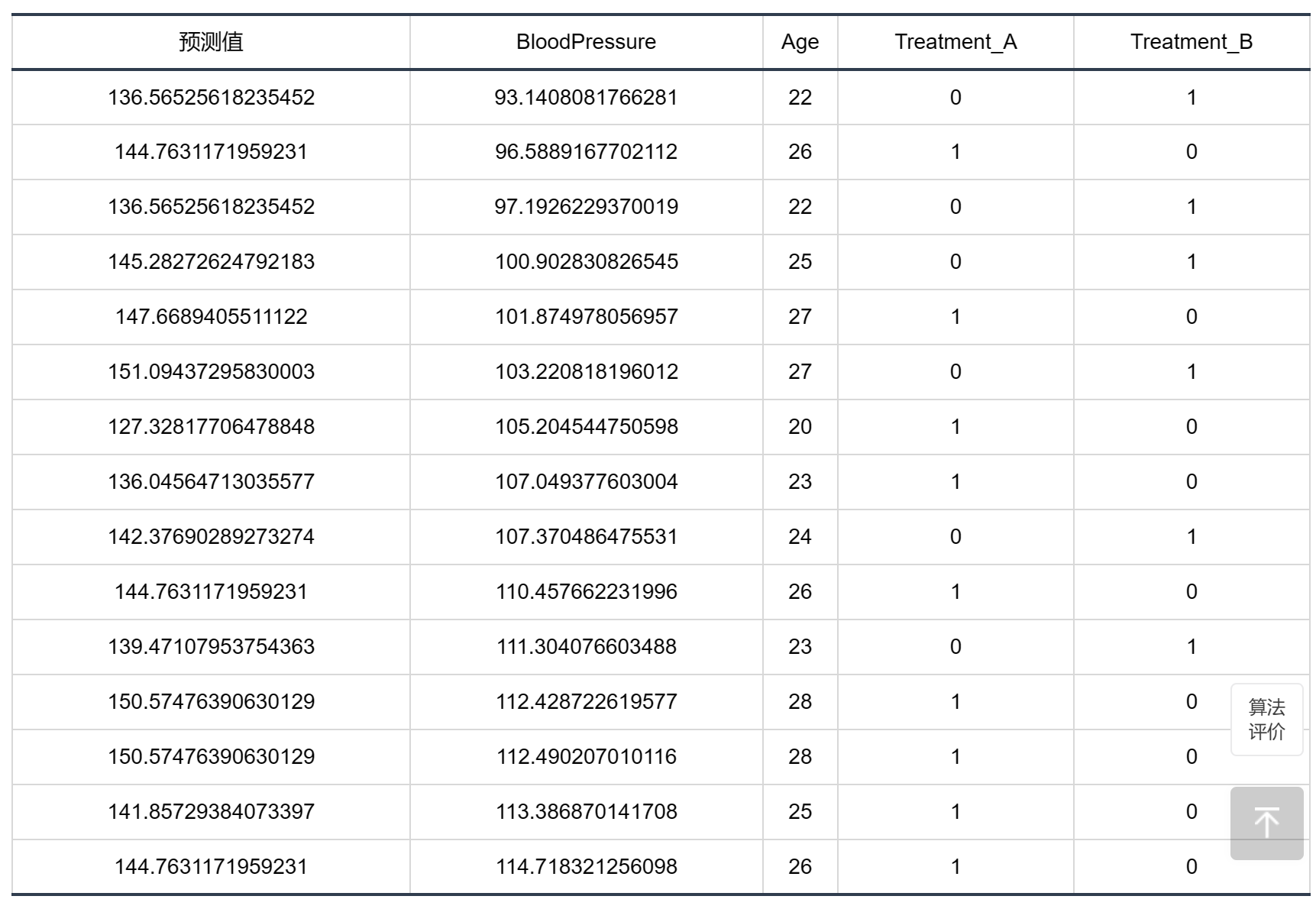

图表说明：上表显示了模型的预测情况。若是数据结果超过15行，点击表格右上角的下载按钮导出全部数据结果。

# 7、注意事项

综合考虑因变量的类型、分布，选择适合数据的 GLM 模型；

# 8、模型理论

广义线性模型是统计学中一类用于建模和分析的框架，适用于因变量不一定服从正态分布的情况。GLM 的一般形式如下：

其中：

g(μ) 是一个链接函数（Link function），它用于将预测的线性组合与均值_μ_ 相联系。
μ 是因变量的均值。
_β_0,_β_1,…,βk 是模型的系数。
_x_1,_x_2,…,xk 是自变量。
g(⋅) 是一个非线性函数，用于将线性组合转换成均值 μ 的预测值。

GLM 的核心是链接函数，它用于描述因变量均值与预测的线性组合之间的关系。不同的链接函数适用于不同的数据类型，例如：
（1）对于二项分布数据，链接函数是 logit 函数，其中p是成功的概率；

（2）对于有序数据，链接函数也是 logit 函数，p是取值不大于某个有序水平的累计概率；
（3）对于泊松分布数据（计数数据），链接函数是对数函数。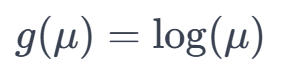
（4）对于高斯分布数据，链接函数是恒等函数，
总体来说，GLM 提供了一种灵活的建模框架，适用于各种类型的数据和不同的分布假设。通过选择合适的链接函数和权重函数，可以适应多样化的数据分析需求。

# 9、手推步骤

Treatment	Age	BloodPressure
A	59	114.7183213
B	55	126.0767401
A	41	112.4287226
B	52	138.0981769
B	36	133.923485
A	39	131.2284298
A	55	131.3732887
A	51	161.3312703
A	59	147.9931024
B	60	168.4041728
A	29	151.2222127
B	38	178.3852231
B	62	197.0592839
B	44	191.4140216
B	68	207.3198245

以线性回归为例，研究药物A、B和年龄对血压的影响。

step1：构造模型
线性回归模型：

y = β_{0} + β_{1} \cdot x_{1} + β_{2} \cdot x_{2}

其中， $x_{1}$ 是Age， $x_{2}$ 是Treatment。

x_{2} = {\begin{cases} 1, & Treatment A \\ 0, & Treatment B \end{cases}

$T r e a t m e n t_{A}$ = 1 表示A组，0 表示B组。
此时模型为

y = β_{0} + β_{1} \cdot Age + β_{2} \cdot {Treatment}_{A}

step2：构造设计矩阵和响应向量
设计矩阵X：

X = [\begin{matrix} 1 & 59 & 1 \\ 1 & 55 & 0 \\ 1 & 41 & 1 \\ 1 & 52 & 0 \\ 1 & 36 & 0 \\ 1 & 39 & 1 \\ 1 & 55 & 1 \\ 1 & 51 & 1 \\ 1 & 59 & 1 \\ 1 & 60 & 0 \\ 1 & 29 & 1 \\ 1 & 38 & 0 \\ 1 & 62 & 0 \\ 1 & 44 & 0 \\ 1 & 68 & 0 \end{matrix}]

响应向量Y：

Y \approx [\begin{matrix} 114.7183 \\ 126.0767 \\ 112.4287 \\ 138.0982 \\ 133.9235 \\ 131.2284 \\ 131.3733 \\ 161.3313 \\ 147.9931 \\ 168.4042 \\ 151.2222 \\ 178.3852 \\ 197.0593 \\ 191.4140 \\ 207.3198 \end{matrix}]

step3：解正规方程
正规方程： $X^{T} X β = X^{T} Y$
计算得到

X^{T} X = [\begin{matrix} 15 & 748 & 7 \\ 748 & 39104 & 333 \\ 7 & 333 & 7 \end{matrix}]

X^{T} Y \approx [\begin{matrix} 2290.9762 \\ 115623.428 \\ 950.2953 \end{matrix}]

代入数据得到 $β_{0} \approx 141.606, β_{1} \approx 0.501, β_{2} \approx - 29.673$ 。
所以最终模型是：

BloodPressure = 141.606 + 0.501 \times Age - 29.673 \times {Treatment}_{A}

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.

建议反馈