泊松分布检验
# 1、作用
泊松分布描述的是一个小概率事件在单位时间内发生的次数,如每个小时进入银行办理业务的人数、报纸上每一页的错别字数量、某个网页的点击量等,简单地说,就是泊松检验的是某种事件是否发生概率很低,且很稳定,同时发生频数的大小之间没有影响关系,例如在一定时间内产品产生的用户需求数,上周发生的用户提的需求数跟这周的没关系。
# 2、输入输出描述
输入:泊松分布检验有两种输入方式,由于泊松分布检验是描述的是一个小概率事件在单位时间内发生的次数,则次数是正整数,是分类离散变量,但是其表现形式可能是数值型(次数),所以对于“单位时间内发生次数”格式,定量或定类的都可以。
- 若是直接输入一连串单位时间内发生次数的序列,要求变量格式为定量或者定类,spsspro 会对单位时间内发生次数进行频数分析后,再进行泊松分布检验。
- 若是已对单位时间内发生次数进行频数分析后,即要输入“单位时间内发生次数”和其对应”频数“,把“频数”放入到加权项中,其中加权项格式为定量。
输出:是否呈现泊松分布。
# 3、案例示例
示例:收集了某上线的产品近 50 个自然周产品每周出 bug 的个数,试检验是否发生概率很低,且很稳定,同时发生频数的大小之间没有影响关系。
# 4、案例数据

泊松分布检验案例数据1(一连串单位时间内发生次数)
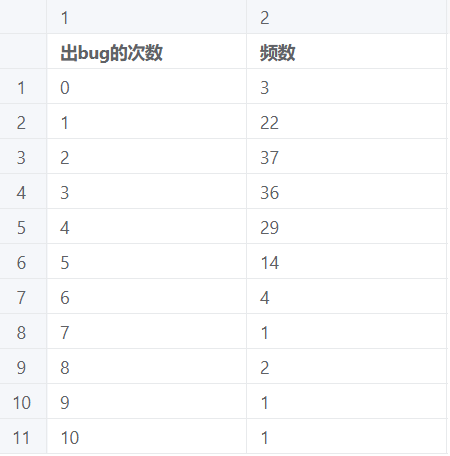
泊松分布检验案例数据2(已对单位时间内发生次数进行频数分析的数据)
# 5、案例操作

Step1:新建项目;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;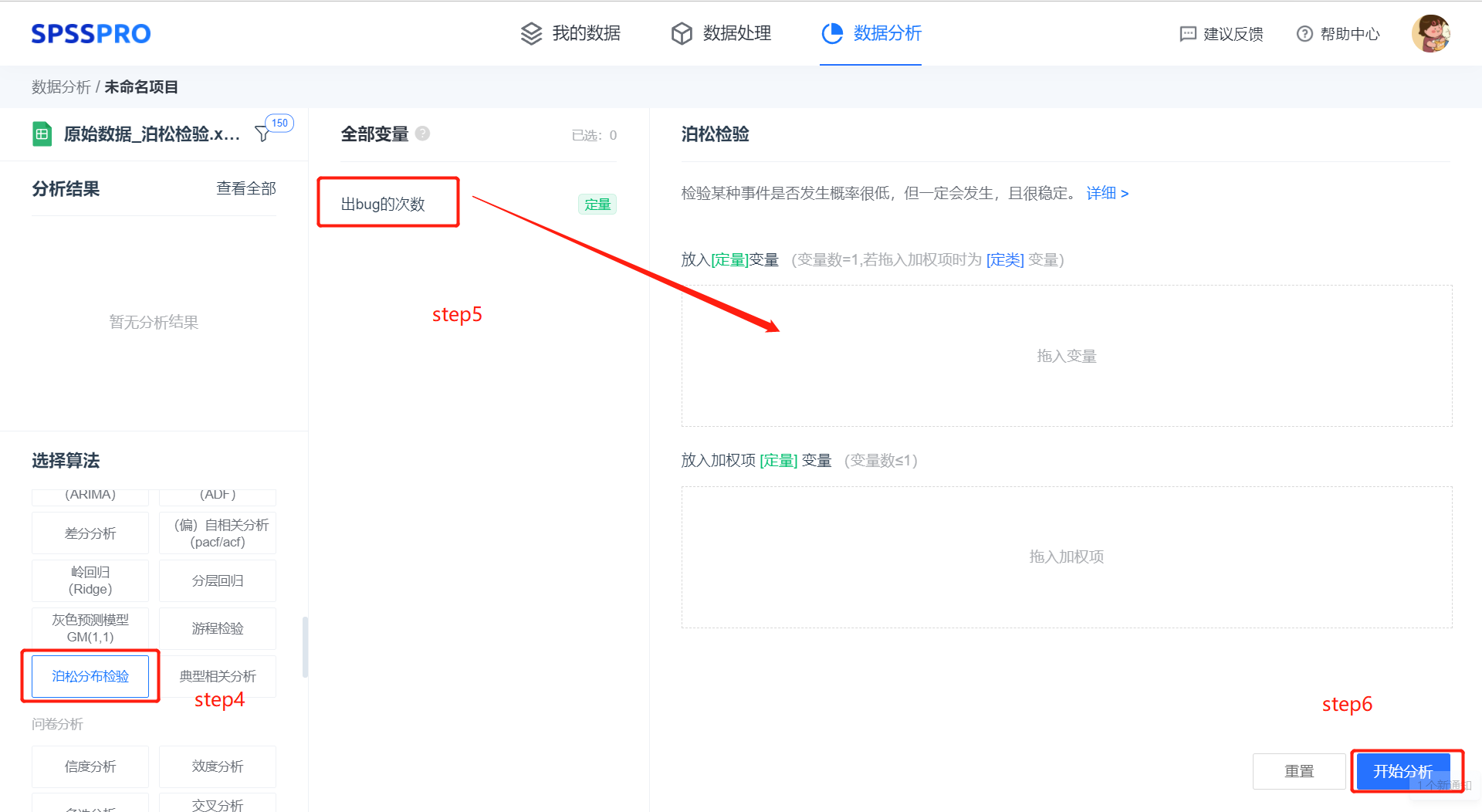
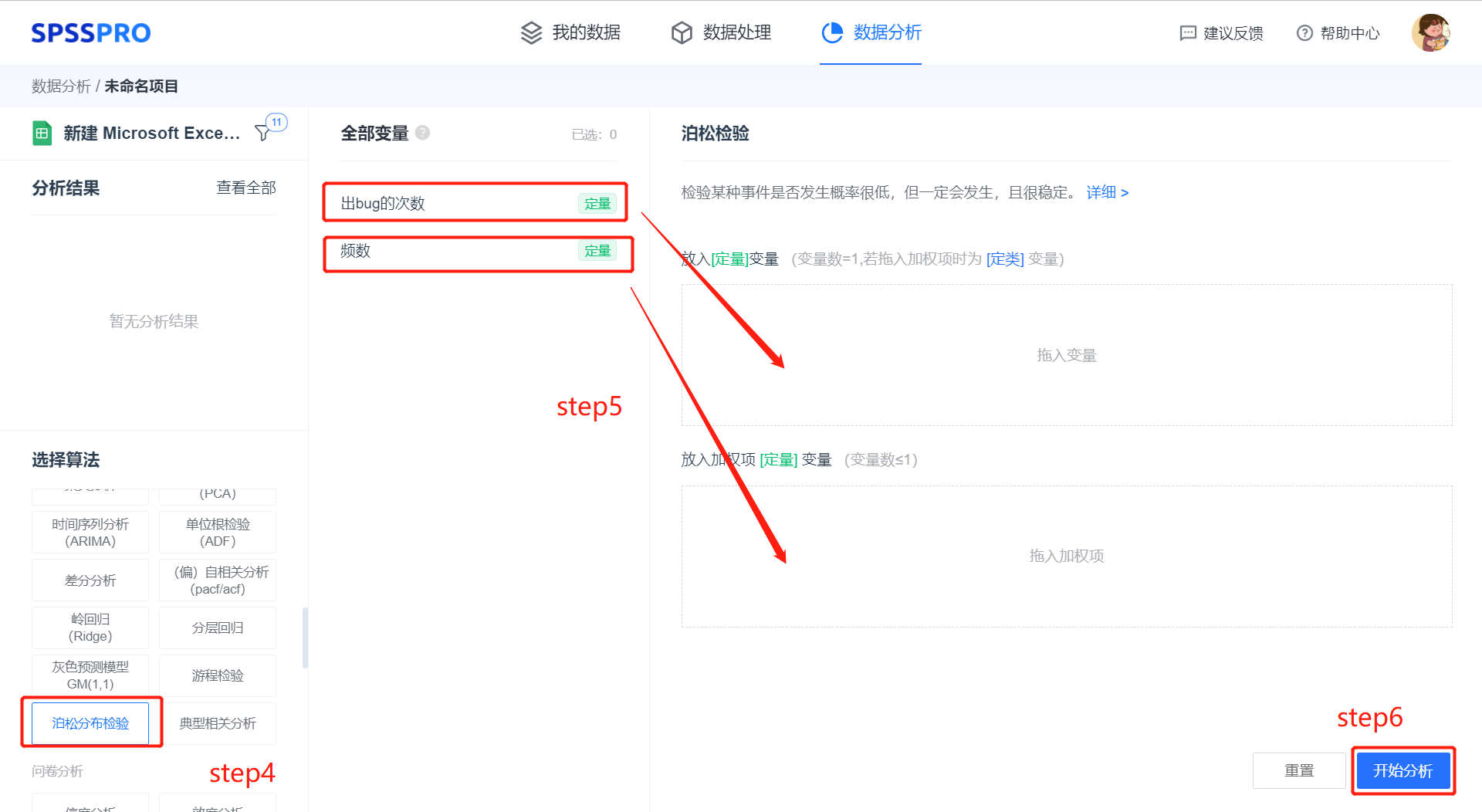
step4:选择【泊松分布检验】;
step5:查看对应的数据数据格式,【泊松分布检验】根据数据不同有两种输入方式,但是结果输出一致。
- 若是直接输入一连串单位时间内发生次数的序列,要求变量格式为定量或者定类,spsspro 会对单位时间内发生次数进行频数分析后,再进行泊松分布检验。
- 若是已对单位时间内发生次数进行频数分析后,即要输入“单位时间内发生次数”和其对应”频数“,把“频数”放入到加权项中,其中加权项格式为定量。
step6:点击【开始分析】,完成全部操作;
# 6、输出结果分析
输出结果 1:Poisson 检验表
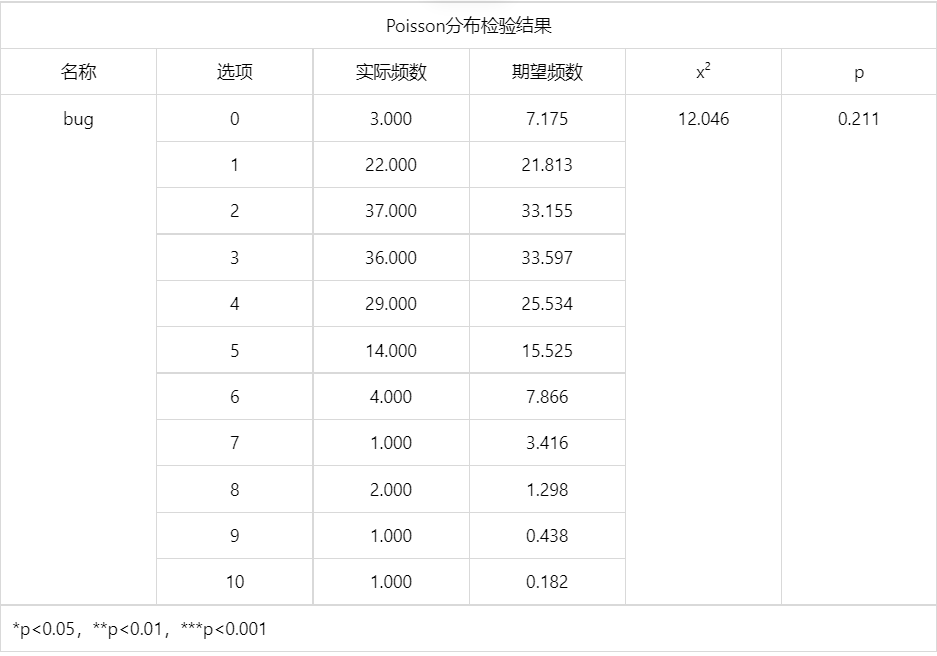
图表说明:上表展示了模型检验的结果,包括频数、选项、期望频数、卡方值 𝑥²、显著性 𝑝 值。 分析选项是否呈现出显著性(𝑝<0.05 或 0.01) 若呈显著性,则拒绝原假设(数据服从泊松分布),数据不服从泊松分布;反之则说明数据服从泊松分布 。
泊松检验的结果显示,不能拒绝原假设,因此数据服从泊松分布,所以 BUG 是会发生的,但是概率很低。
输出结果 2:泊松分布图

图表说明:上表为泊松分布表,其中蓝色的条形柱是实际的观察值,青色的虚线是理论的预期值,用于分析实际频数和理论频数是否差异。可见图中分布基本拟合 lam=3 的泊松分布,故可认为 bug 的出现是一种泊松分布。
# 7、注意事项
- 由于泊松分布的取值为 0 和大于 0 的正整数,故输入数据有两种形式:
- 1)若不输入权数,则数据必须为 0 和大于 0 的正整数,此时的数据为定量。
- 2)若输入权数,则数据为定类数据,而权数代表发生的频次。
- 在 poisson 检验表中:
- 1)若不输入权数:
- 若最大值减去最小值+1 的值小于 200,则中间的空值会自动补全,然后取去重次数。
- 若大于 200,则直接按期望值计算。
- 2)若输入权数,则直接按期望值计算。
- 1)若不输入权数:
# 8、模型理论
泊松分布的拟合检验:在长为 t 的时间间隔内观测事件 A 发生的次数 X(t),将这样的观测重复进行 m 次,
记 Ai={X(t)=i}(i = 0,1,2,…,n)为一次观测中事件 A 发生 i 次这个事件。A0,A1,…An 在 m 次观测中出现的频数分别为 m0,m1,…,mn,且![]() 。
。
上述假定用到以下事实:即使是泊松分布, 重复观测 m 次时,也只能观测到有限个不同的值,我们需要检验的假设为事件流 X(t)是否服从泊松分布 P(λ),其中 P 为未知参数。将检验的假设 X(t) ~ p(λ)转化为检验以下假设:

这里有一个未知参数 λ,采用极大似然估计:
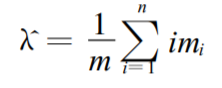
将λ代入第二个公式可以估计出pi。可用X2检验H0检验统计量:
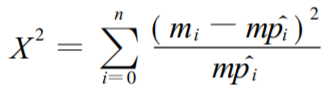
在H0成立时近似服从自由度为n+1-1-1 = n-1的X2分布。给定显著性水平α,可得H0的拒绝域为:
![]()
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com. (opens new window)
[2]刘瑞元,张智霞.二项分布与泊松分布判别的假设检验[J].青海大学学报(自然科学版),2008,(01):44-47.2000.
[3] 魏宗舒.概率论与数理统计教程[ M] .北京:高等教育出版社, 1983.
