广义估计方程

# 广义估计方程

# 1、作用

广义估计方程（GEE）要用于处理具有相关性结构的数据，如重复测量数据、集群数据或纵向数据，其中观测点之间可能存在相关性。它是在广义线性模型（GLM）关注因变量与自变量的关系的基础上，还关注相关性参数的估计，通过考虑相关性结构来更准确地估计模型参数。

# 2、输入输出描述

输入：1个定量因变量；1个或以上的自变量，1个个体项变量，1个重复项变量。
输出：重复变量相关性结构，以及考虑相关性结构后估计模型参数。，

# 3、案例示例

案例：假设正在研究某种药物对患者的治疗效果，并每天在30个时点去测量患者的血压，用广义估计方程去研究药物对患者的治疗效果。

# 4、案例数据

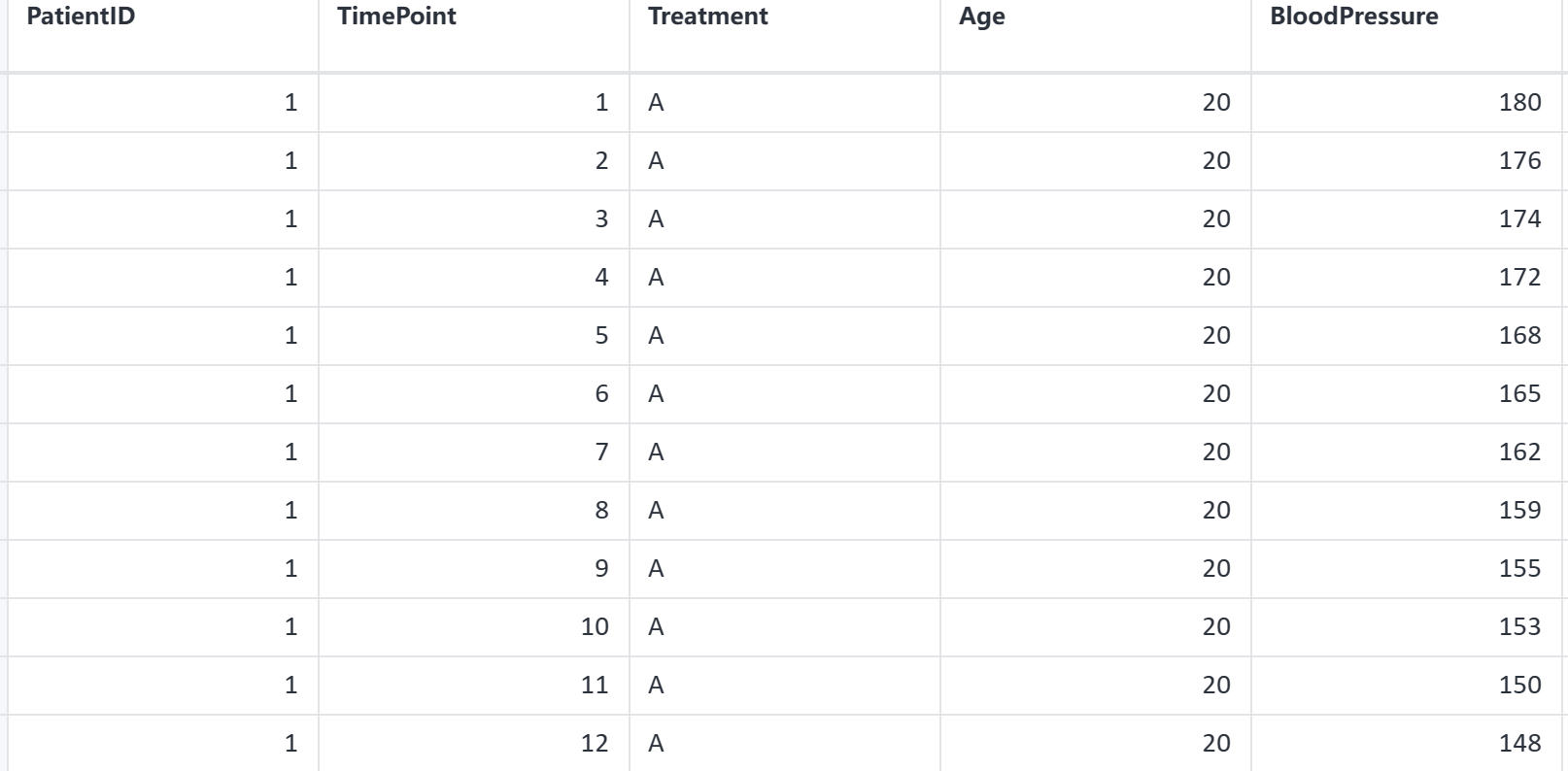
广义估计方程案例数据

# 5、案例操作

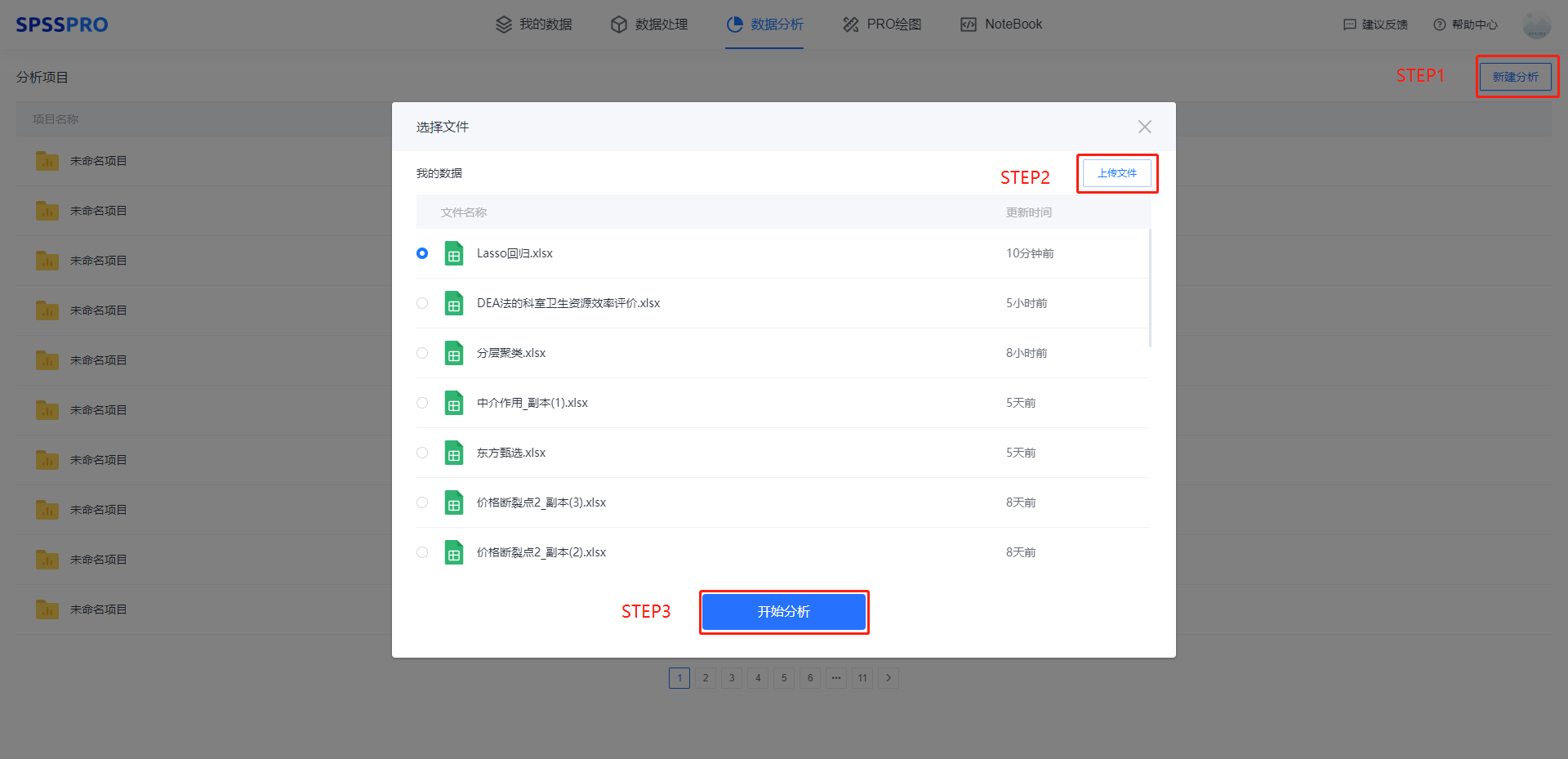
Step1：新建分析；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；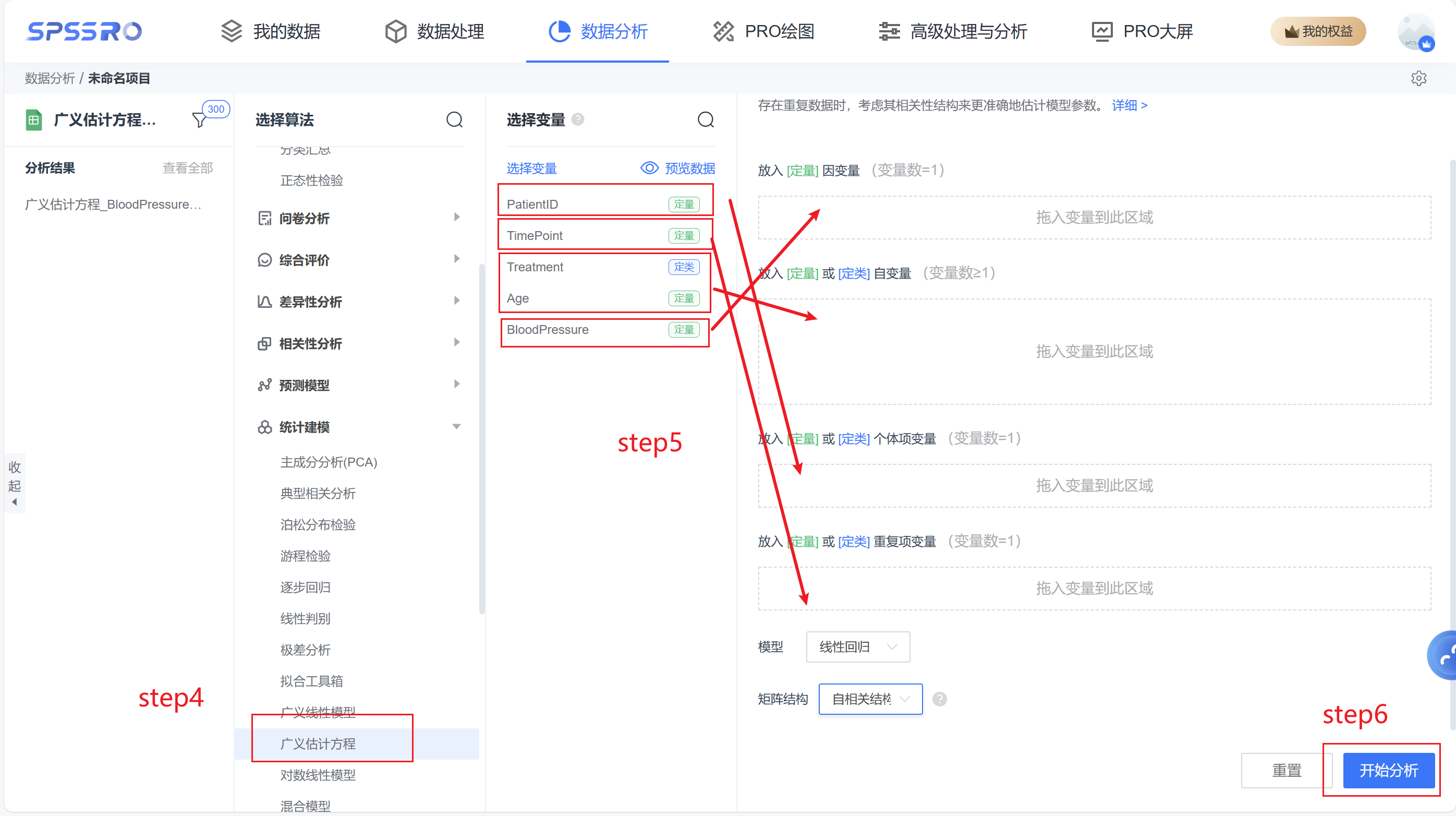

step4：选择【广义估计方程】；
step5：查看对应的数据数据格式，按照【广义估计方程】要求拖入变量。
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果1：参数估计

参数	系数	标准误差	Wald	P	95%置信区间下限	95%置信区间上限
const	152.168	25.94	34.411	0.000***	101.326	203.01
Age	0.079	0.546	0.021	0.885	-0.991	1.149
Treatment_A	-12.818	13.242	0.937	0.333	-38.772	13.136
Treatment_B	2.258	7.786	0.084	0.772	-13.003	17.519

图表说明：上表展示了参数估计的结果，由于广义估计方程考虑了重复变量相关性，能够更准确地估计模型参数和标准误差。

输出结果2：工作相关矩阵

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1.00	0.94	0.89	0.85	0.80	0.76	0.72	0.68	0.65	0.61	0.58	0.55	0.52	0.49	0.47
0.94	1.00	0.94	0.90	0.85	0.81	0.77	0.73	0.69	0.65	0.62	0.59	0.56	0.53	0.50
0.89	0.94	1.00	0.95	0.90	0.85	0.81	0.77	0.73	0.69	0.65	0.62	0.59	0.56	0.53
0.85	0.90	0.95	1.00	0.95	0.90	0.85	0.81	0.77	0.73	0.69	0.65	0.62	0.59	0.56
0.81	0.85	0.90	0.95	1.00	0.95	0.90	0.85	0.81	0.77	0.73	0.69	0.65	0.62	0.59
0.77	0.81	0.85	0.90	0.95	1.00	0.95	0.90	0.85	0.81	0.77	0.73	0.69	0.65	0.62
0.73	0.77	0.81	0.85	0.90	0.95	1.00	0.95	0.90	0.85	0.81	0.77	0.73	0.69	0.65
0.69	0.73	0.77	0.81	0.85	0.90	0.95	1.00	0.95	0.90	0.85	0.81	0.77	0.73	0.69
0.65	0.69	0.73	0.77	0.81	0.85	0.90	0.95	1.00	0.95	0.90	0.85	0.81	0.77	0.73
0.62	0.65	0.69	0.73	0.77	0.81	0.85	0.90	0.95	1.00	0.95	0.90	0.85	0.81	0.77
0.59	0.62	0.65	0.69	0.73	0.77	0.81	0.85	0.90	0.95	1.00	0.95	0.90	0.85	0.81
0.56	0.59	0.62	0.65	0.69	0.73	0.77	0.81	0.85	0.90	0.95	1.00	0.95	0.90	0.85
0.53	0.56	0.59	0.62	0.65	0.69	0.73	0.77	0.81	0.85	0.90	0.95	1.00	0.95	0.90
0.50	0.53	0.56	0.59	0.62	0.65	0.69	0.73	0.77	0.81	0.85	0.90	0.95	1.00	0.95
0.47	0.50	0.53	0.56	0.59	0.62	0.65	0.69	0.73	0.77	0.81	0.85	0.90	0.95	1.00

图表说明：上表展示了重复变量的相关结构矩阵。因为题目中的数据，每一个个体涉及到30次重复数据，所以会产生一个30*30的工作相关矩阵，若是超过15阶的矩阵，输出报告篇幅有限，需要点击表格右上角的下载按钮下载数据。

输出结果3：预测结果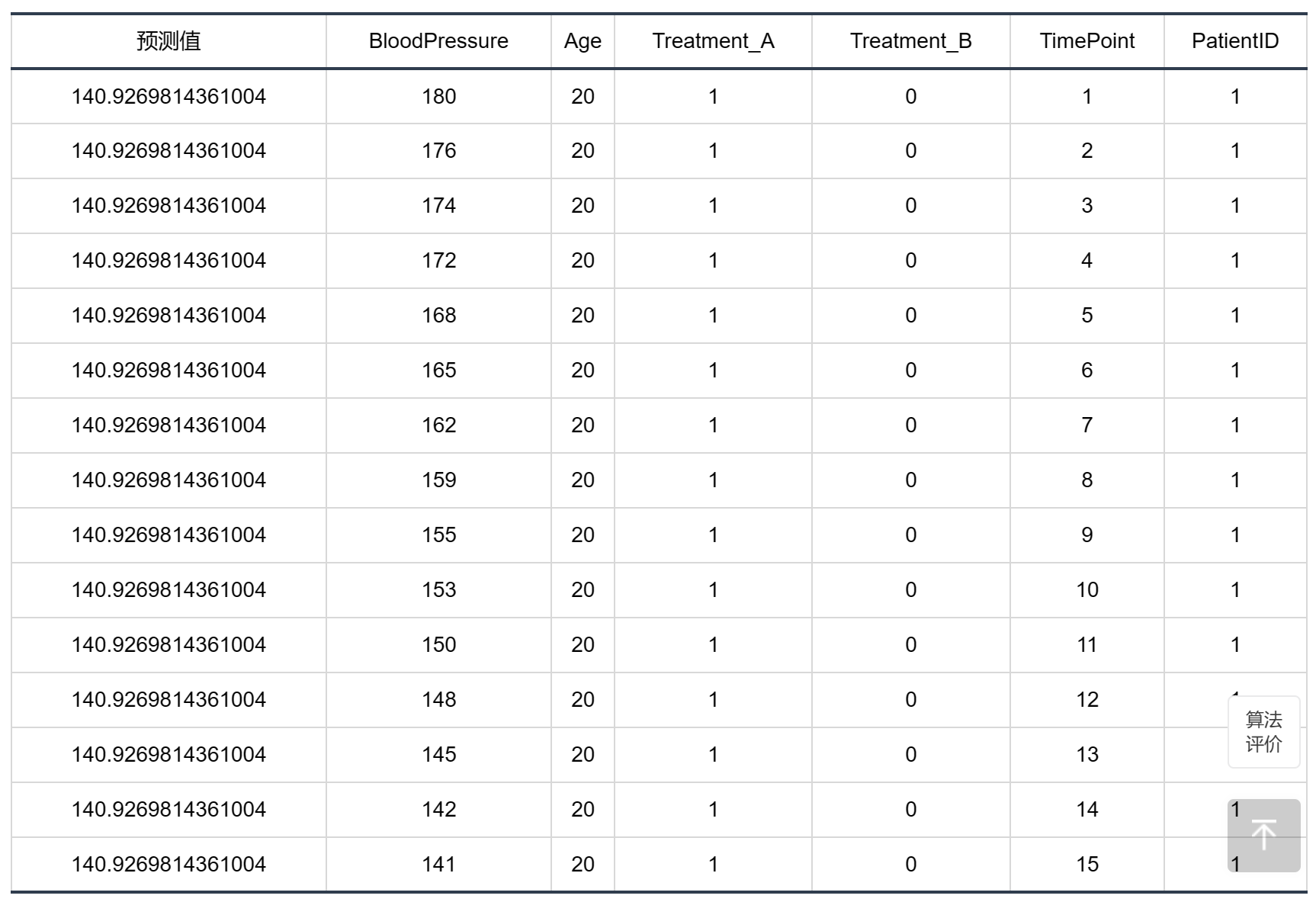

图表说明：上表显示了模型的预测情况。若是数据结果超过15行，点击表格右上角的下载按钮导出全部数据结果。

# 7、注意事项

综合考虑因变量的类型、分布，选择适合数据的GEE模型；
根据重复变量实际特性选择广义估计方程的协方差矩阵结构：

独立结构，它假定观测值之间没有相关性，即它们是相互独立的。
交换结构，它假定观测值之间的相关性相等且对称，通常用于描述不同组内观测值的相关性。
一阶自相关结构，其中相邻时间点之间存在相关性。

# 8、模型理论

广义估计方程（Generalized Estimating Equations，GEE）是一种用于处理相关数据的统计方法，通常用于建模重复测量或群集化的数据。GEE 通过建立广义估计方程来估计参数，而不需要过多关于数据分布的先验假设。以下是 GEE 的基本公式和原理：
考虑观测单位 i 在时间 t 的观测 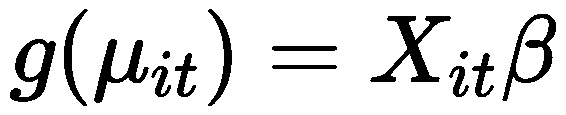Y_it，与自变量 X_it 之间的关系被建模为：

其中：

g(⋅) 是一个链接函数，将均值 μ_it 与自变量 X_it 的线性组合关联起来。
_μ_it_是观测 Y_it 的均值。
X_it 是包含观测 Y_it 的自变量的矩阵。
β 是待估计的参数向量。

将模型的形式写成一个广义估计方程，形式为：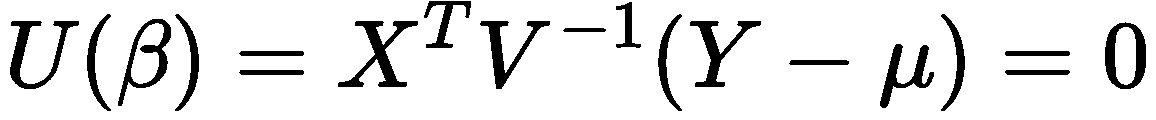

其中 U(β) 是一个方程，X 是设计矩阵，V 是观测数据的工作结构矩阵，Y 是观测数据的响应，μ 是均值，β 是参数。
对于重复测量数据，协方差矩阵 V 考虑了观测单位内观测之间的相关性。例如，如果测量来自同一观测单位的多个时间点，V 可以包含对角线元素表示时间点内的方差，非对角线元素表示时间点间的协方差。GEE 通过考虑协方差结构，使得模型更能适应具有相关性结构的数据，如重复测量或集群化的数据。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.

建议反馈