三因素方差分析
# 1、作用
在现实研究中,一个变量的影响可能不足以说明差异效果,当方差分析中涉及三个定类自变量时,称为三因素方差分析,用于分析三个自变量对因变量带来的显著性影响。
# 2、输入输出描述
输入:三个定类变量(如电脑的品牌、广告形式和生产地区)与一个定量变量(如电脑销量)
输出:模型三因素方差分析的结果:变量一对定量变量产生/不产生显著性影响,变量二对定量变量产生/不产生显著性影响,变量三对定量变量产生/不产生显著性影响,均值对比图。
# 3、案例示例
案例:分析品牌、地区和广告形式三个定类自变量对电脑销量(定量因变量)的影响。
# 4、案例数据
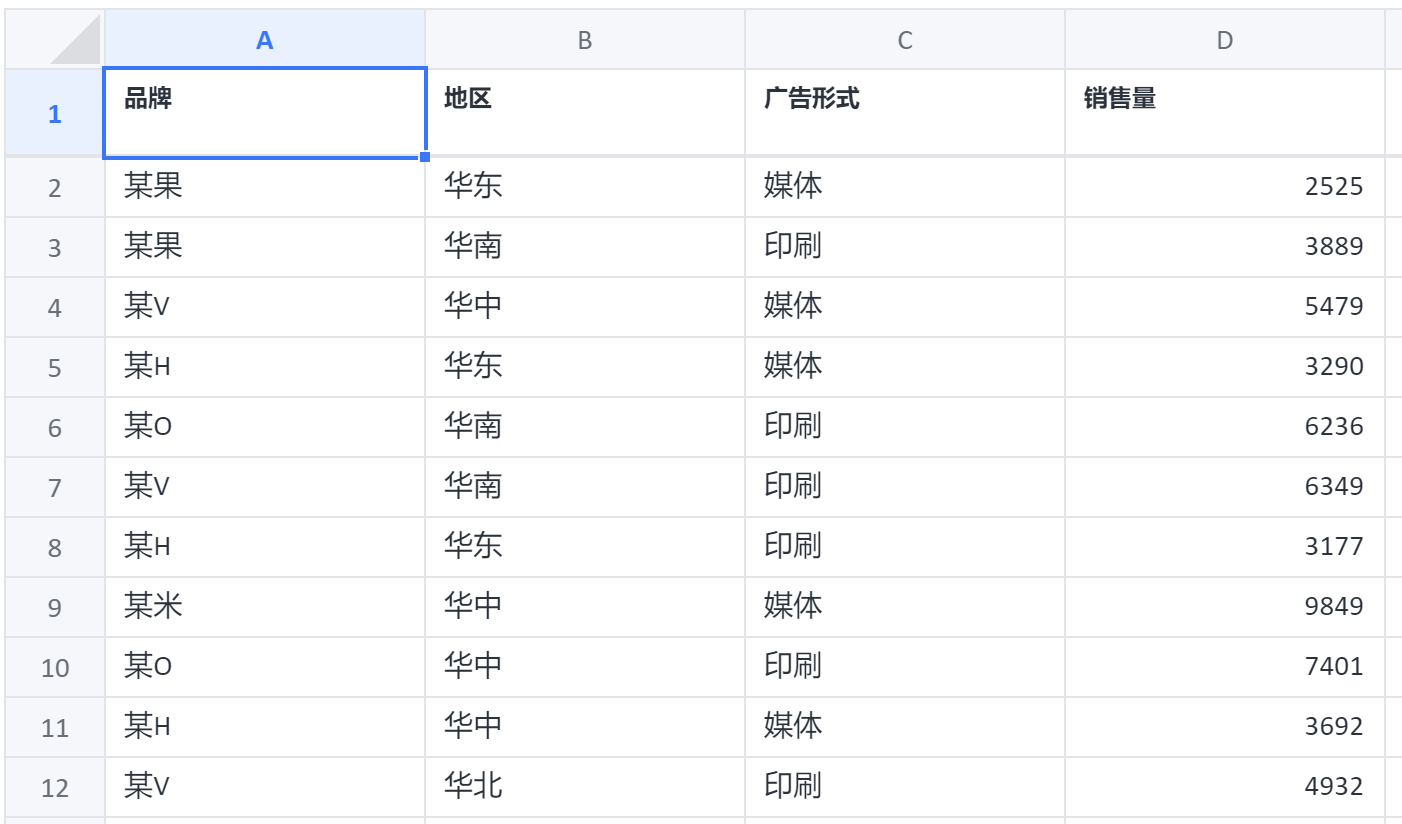
三因素方差分析案例数据
# 5、案例操作
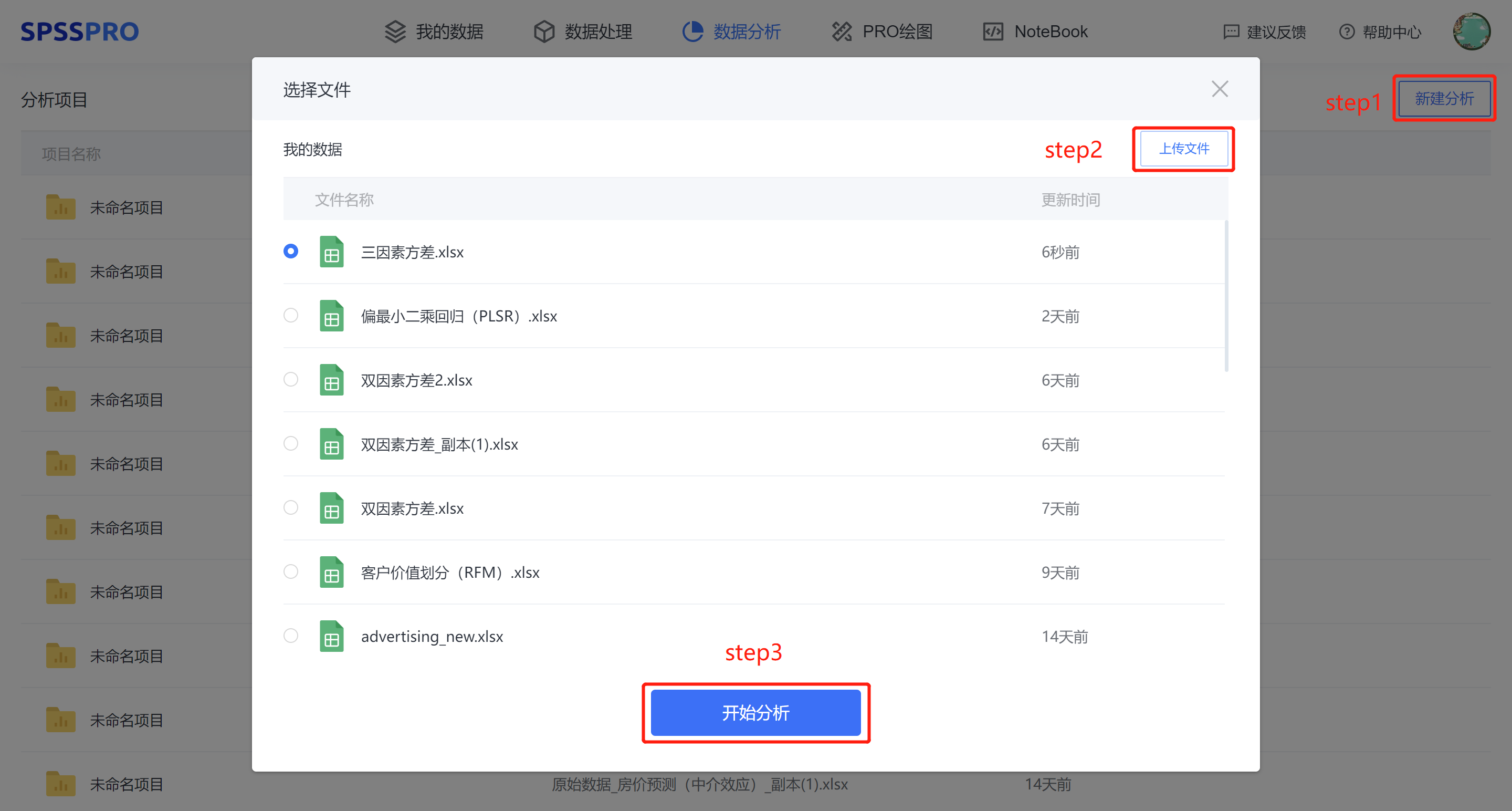
Step1:新建项目;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;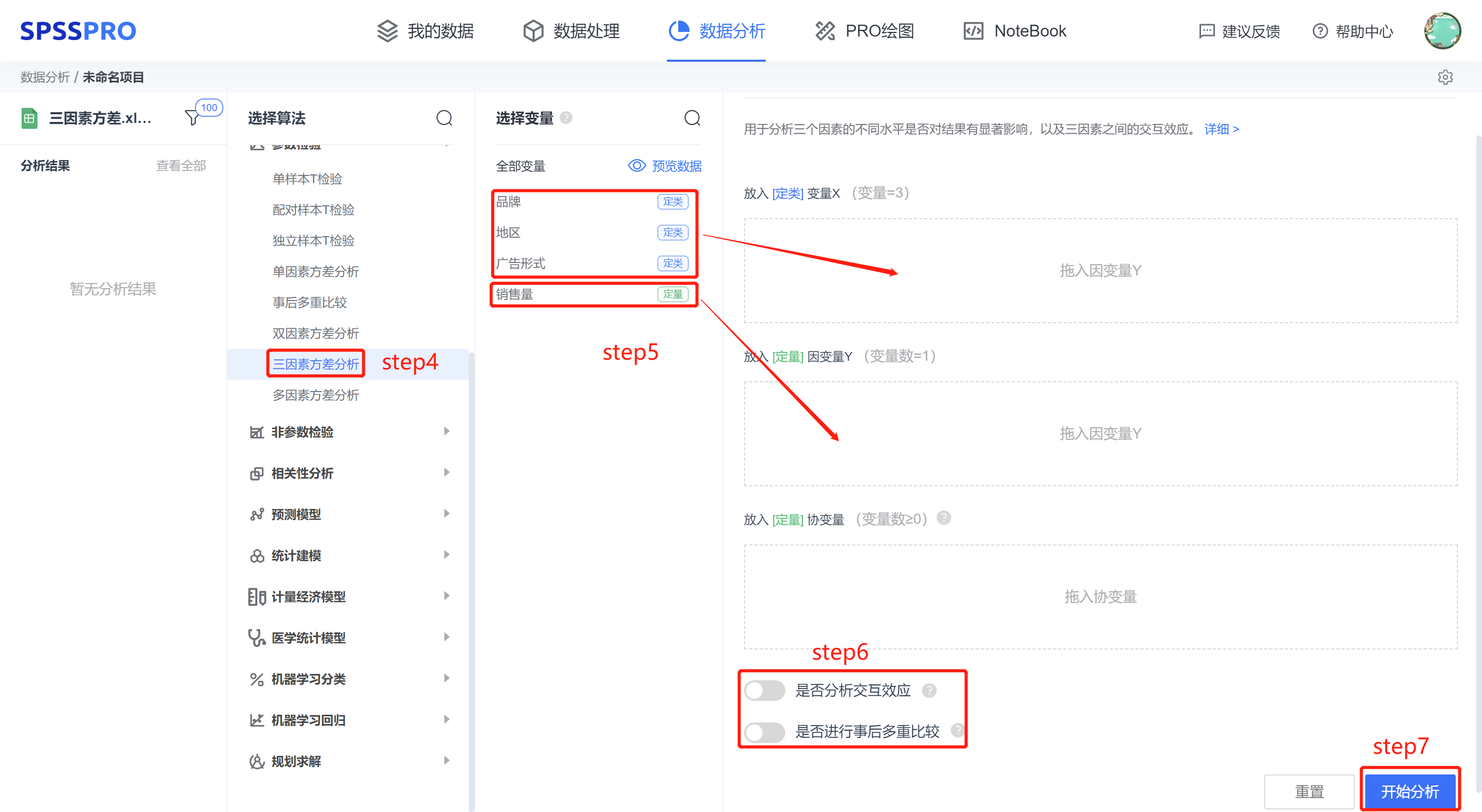
step4:选择【三因素方差分析】;
step5:查看对应的数据数据格式,【三因素方差分析】要求输入数据为分组定类变量,变量数=3;放入定量变量,变量数为 1 项;
step6:进行相关设置;
step7:点击【开始分析】,完成全部操作。
# 6、输出结果分析
输出结果 1:三因素方差分析结果
| 项 | 平方和 | 自由度 | 均方 | F | p |
|---|---|---|---|---|---|
| 截距 | 2649689679.717 | 1 | 2649689679.717 | 3601.38 | 0.000**_ |
| 广告形式 | 8428.282 | 1 | 8428.282 | 0.011 | 0.915 |
| 地区 | 38251430.782 | 3 | 12750476.927 | 17.33 | 0.000_** |
| 品牌 | 286834540.466 | 4 | 71708635.117 | 97.464 | 0.000*** |
| 误差 | 66952596.343 | 91 | 735742.817 | NaN |
R 方=0.852(调整后 R 方=0.839)
图表说明:上表展示了三因素方差分析的结果,主效应如果显著可以进一步分析事后多重分析结果。
**智能分析**:三因素方差结果显示: 对于变量截距,从 F 检验的结果分析可以得到,显著性 P 值为 0.000、***水平上呈现显著性,对结果有显著性影响,存在主效应。 对于变量广告形式,从 F 检验的结果分析可以得到,显著性 P 值为 0.915 水平上不呈现显著性,对结果没有显著性影响,不存在主效应。 对于变量地区,从 F 检验的结果分析可以得到,显著性 P 值为 0.000***水平上呈现显著性,对结果有显著性影响,存在主效应。 对于变量品牌,从 F 检验的结果分析可以得到,显著性 P 值为 0.000***水平上呈现显著性,对结果有显著性影响,存在主效应。
输出结果 2:均值对比图
图表说明:上图展示了三因素方差分析的均值的结果,通过比较不同分组变量的均值以及交叉情况(通常有交叉则有交互作用),可以挖掘其差异关系。
# 7、注意事项
- 每一个总体都服从正态分布,且有相同的方差。
- 需考虑是否是重复测量/是否满足独立性假设。
- 需考虑三个因素之间是否有交互作用,有交互作用可以在算法界面选择分析交互作用。
# 8、模型理论
# 1.介绍
方差分析又称“变异数分析”或“F 检验”,用于对两个及两个以上样本均数差别的显著性检验。三因素方差分析是检验在三种因素影响下,三个以上总体的均值之间是否相等的一种统计方法。包括无交互影响和有交互影响的情况。
# 2.原理
1.模型建立
假设有三个因素 A, B, C,因素 A 有 r 个水平,记为![]() ;因素 B 有 s 个水平,记为
;因素 B 有 s 个水平,记为![]() ;因素 C 有 t 个水平,记为
;因素 C 有 t 个水平,记为![]() 。在水平组合
。在水平组合![]() 下样本相互独立,且
下样本相互独立,且![]() 。
。![]() 是全部样本数据的总平均值:
是全部样本数据的总平均值:![]() ,
,![]() 是因素 A 的第 i 个水平下各观察值的平均值:
是因素 A 的第 i 个水平下各观察值的平均值: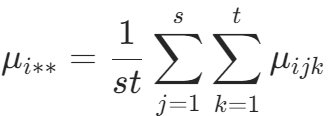 ,
,![]() 是因素 B 的第 j 个水平下各观察值的平均值:
是因素 B 的第 j 个水平下各观察值的平均值: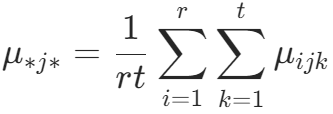 ,
,![]() 是因素 C 的第 k 个水平下各观察值的平均值:
是因素 C 的第 k 个水平下各观察值的平均值: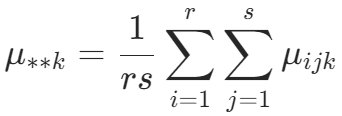 ,
,![]() 为因素 A 的第 i 个水平的效应,
为因素 A 的第 i 个水平的效应,![]() 为因素 B 的第 j 个水平的效应,
为因素 B 的第 j 个水平的效应,![]() 为因素 C 的第 k 个水平的效应,分别为:
为因素 C 的第 k 个水平的效应,分别为: ![]() 。他们分别满足:
。他们分别满足: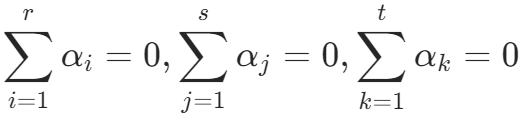
若![]() ,则模型为:
,则模型为: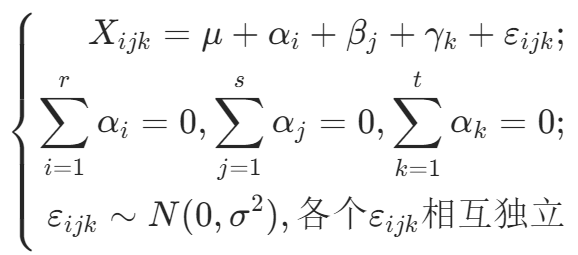
2.提出假设
为了检验三个因素的影响,需要对三个因素分别提出以下假设:
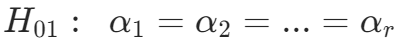 ,A 因素(自变量)对因变量没有显著影响;
,A 因素(自变量)对因变量没有显著影响;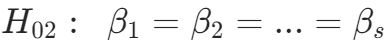 ,B 因素(自变量)对因变量没有显著影响;
,B 因素(自变量)对因变量没有显著影响;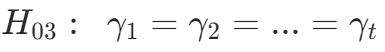 ,C 因素(自变量)对因变量没有显著影响。
,C 因素(自变量)对因变量没有显著影响。
3.构造检验的统计量
为检验假设是否成立,需要分别确定检验因素的统计量。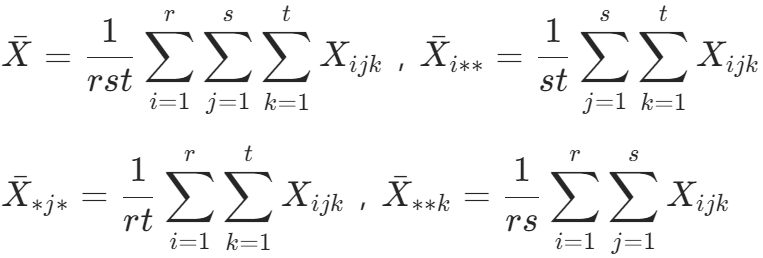
引入 ,则
,则
因素 A 所产生的误差平方和为: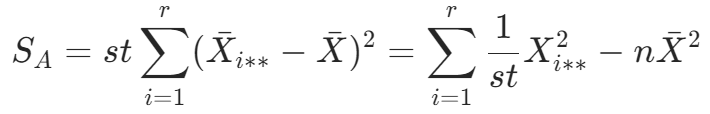
因素 B 所产生的误差平方和为:
因素 C 所产生的误差平方和为: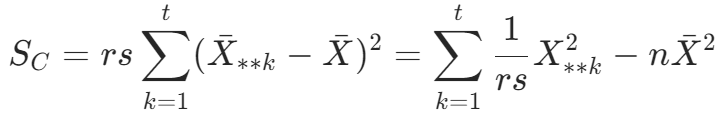
随机误差平方和: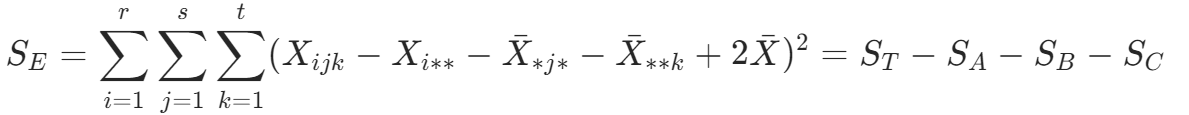
4.三因素方差分析表

5.检验规则
- 若
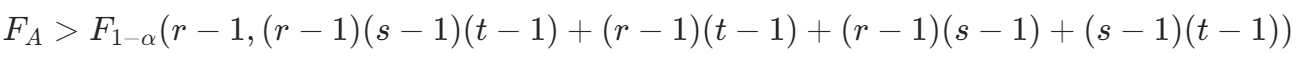 ,则拒绝
,则拒绝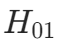 ,表示在因素 A 的各水平下的效应有显著差异;
,表示在因素 A 的各水平下的效应有显著差异; - 若
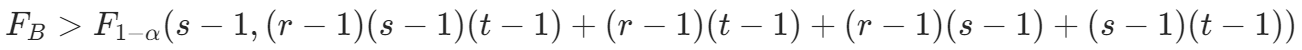 ,则拒绝
,则拒绝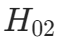 ,表示在因素 B 的各水平下的效应有显著差异;
,表示在因素 B 的各水平下的效应有显著差异; - 若
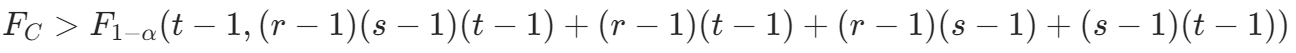 ,则拒绝
,则拒绝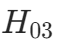 ,表示在因素 C 的各水平下的效应有显著差异。
,表示在因素 C 的各水平下的效应有显著差异。
以上介绍为无交互影响的三因素方差分析,若需分析有有交互影响的情况,只需在上面案例操作 step6:进行相关设置即可。
# 9、参考文献
[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2] 郭萍. 三因素方差分析的原理及应用[J]. 沈阳大学学报(自然科学版),2015,27(1):40-43. DOI:10.3969/j.issn.2095-5456.2015.01.009.