多变量方差分析

# 1、作用

多变量方差分析（MANOVA）的目标是综合考虑多个因变量，去分析分组因素是否会对多个因变量整体上具有差异性。若是结果显示有差异，可以通过主体效应检验去查看具体是对哪一个因变量有着显著的差异影响。

# 2、输入输出描述

输入：2个及以上定量因变量；1个及以上的定类分组变量；0个及以上的定量协变量。
输出：分组因素是否会对多个因变量整体上具有差异性。

# 3、案例示例

案例：一个制药公司正在研究一种新药的疗效。研究对象是患有某种疾病的患者。研究设计包括两个治疗组别：Treatment A 和 Treatment B。研究人员感兴趣的是在不同组别之间比较三个因变量：患者的生存率、症状改善程度和生活质量。

# 4、案例数据

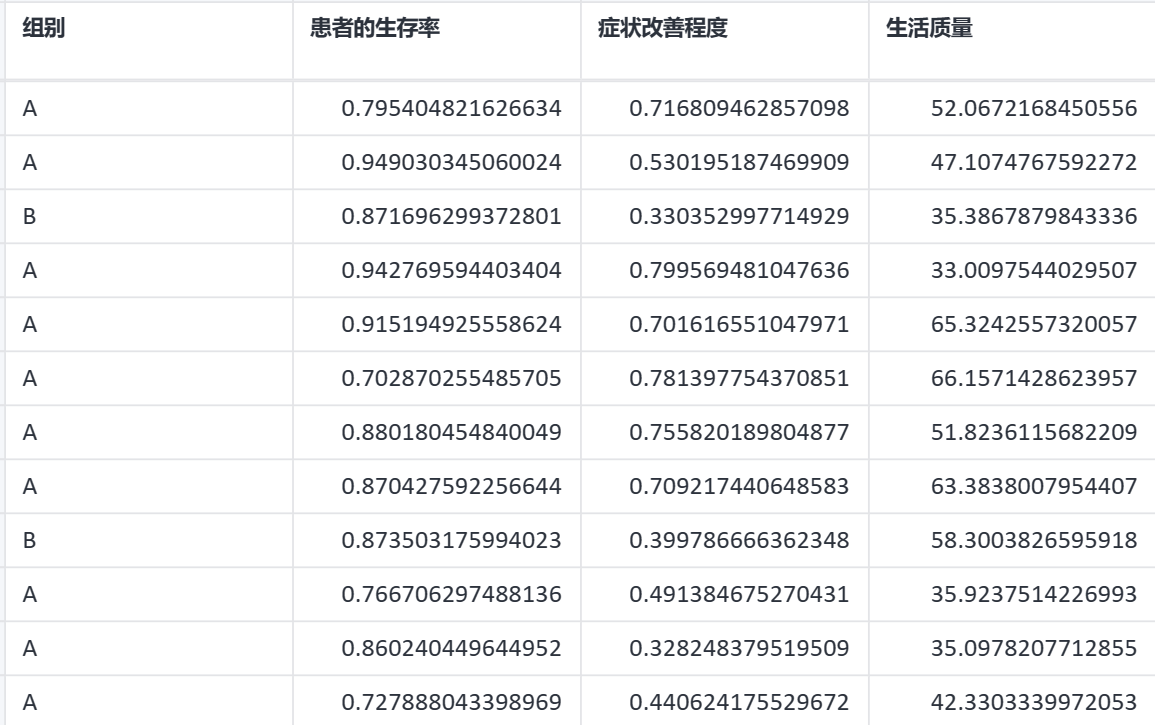
案例数据

# 5、案例操作

Step1：新建项目；
Step2：上传数据；
Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

step4：选择【多变量方差分析】；
step5：查看对应的数据数据格式，按要求拖入数据，
step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果1：多变量检验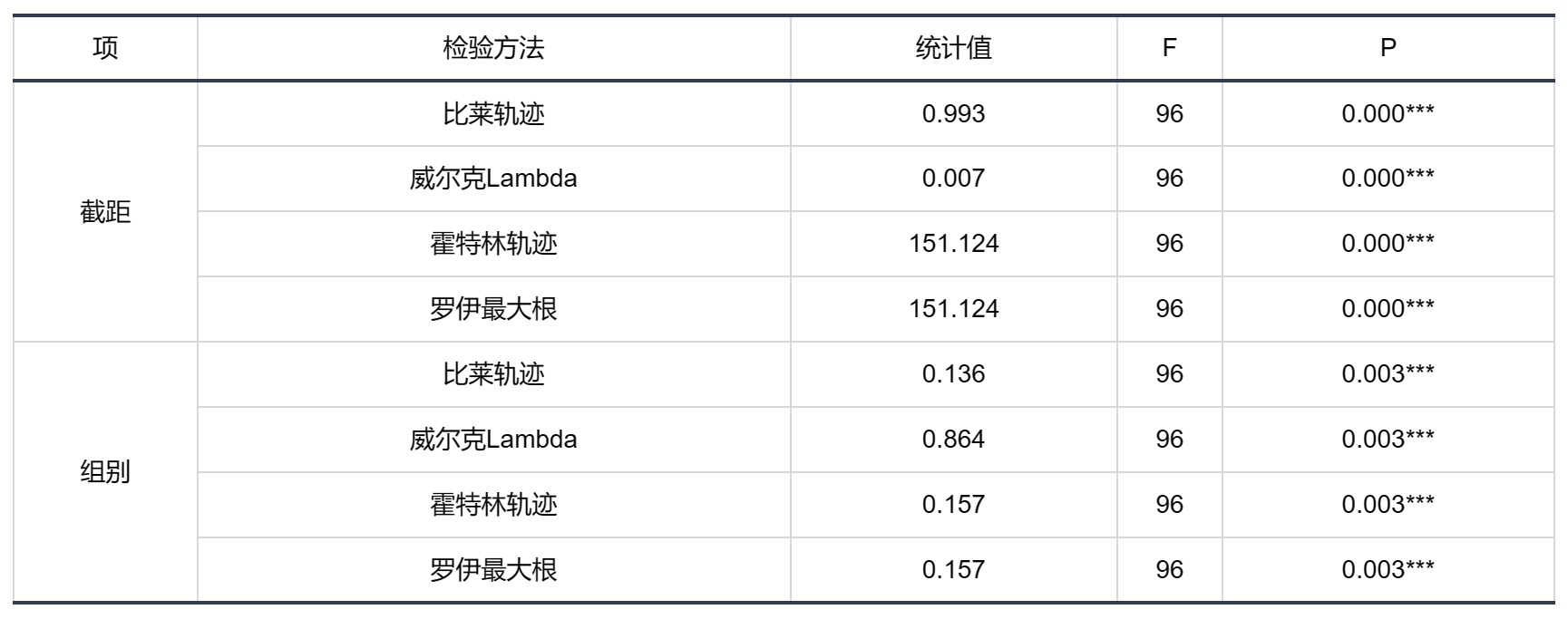

图表说明：上表展示了多变量检验的结果，用于研究中不同组别在多个因变量方面总体上是否存在显著差异。
● Wilks' Lambda（威尔克Lambda）：值范围从 0 到 1，较小的值表示组别之间的多个因变量存在较大的总体差异。若 Wilks' Lambda 的 P< 0.05，拒绝原假设，认为组别之间存在差异。
● Pillai's Trace（比莱轨迹）：值范围从 0 到正无穷，较小的值表示组别之间存在较大的总体差异。若Pillai's Trace 的 P< 0.05，拒绝原假设，认为组别之间存在差异。
● Hotelling-Lawley Trace（霍特林轨迹）：值范围从 0 到正无穷，较小的值表示组别之间存在较大的总体差异。若Hotelling-Lawley Trace 的 P< 0.05，拒绝原假设，认为组别之间存在差异。
● Roy's Largest Root（罗伊最大根）：值范围从 0 到正无穷，较小的值表示组别之间存在较大的总体差异。若Roy's Largest Root的 P< 0.05，拒绝原假设，认为组别之间存在差异。如果结果显著，那么你可以进一步进行后续分析，可以通过主体效应检验去查看具体是对哪一个因变量有着显著的差异影响。
解释结果时，常用的 Wilks' Lambda，但建议综合考虑这些指标，而不是仅仅依赖于一个。如果这些指标的结果一致，那么你对组别之间的差异更有信心。

输出结果2：主体间效应检验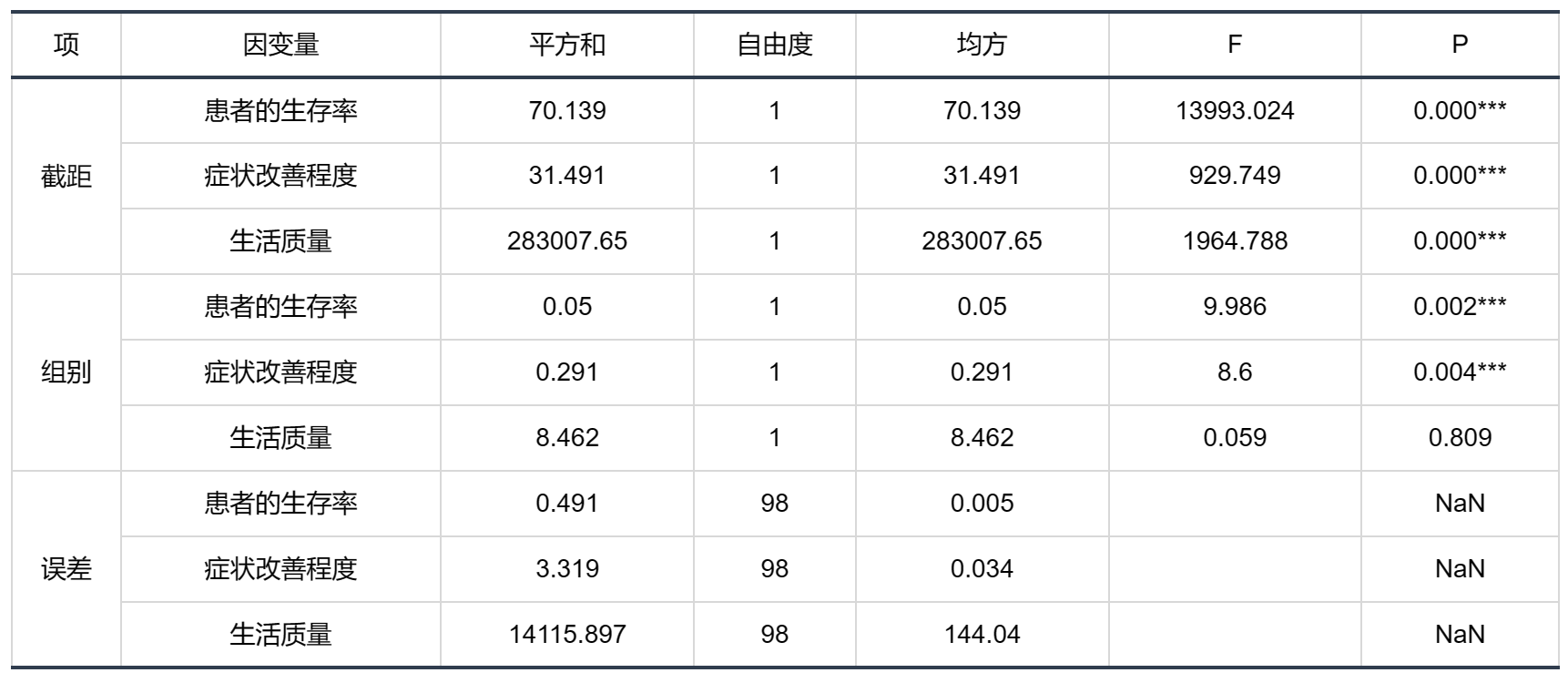

图表说明：上表展示了主体间效应检验的结果，可以通过主体效应检验去查看具体是对哪一个因变量有着显著的差异影响。由结果可知，治疗组别会对患者的生存率和症状改善程度有影响，对生活质量没有影响。

# 7、注意事项

保持组别之间的均衡，并确保每个组别中的观测值足够多。不平衡的组别可能导致对 MANOVA 结果的不准确解释。

# 8、模型理论

考虑有k个组别，每个组别有p个因变量，总共有n个观测值。我们将观测到的数据表示为X矩阵，其中：

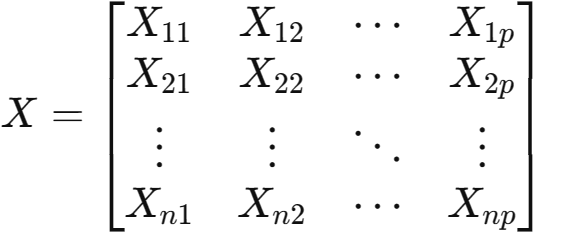
其中，X_ij 表示第i个观测值在第j个变量上的取值。

在多变量方差分析（MANOVA）中，W 表示组内变异的协方差矩阵，B 表示组间变异的协方差矩阵。这两个协方差矩阵的计算涉及到对观测值的分组和变异的度量。
(1)组内变异的协方差矩阵 W：
组内变异表示在每个组别内部的数据变异。W 的计算涉及到每个组别内观测值之间的协方差。给定第 i 个组别，其数据矩阵表示为 X_i，则 W 的计算公式为：

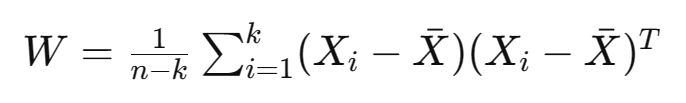
(2)组间变异的协方差矩阵 B：
组间变异表示不同组别之间的数据变异。B 的计算涉及到每个组别的均值之间的协方差。给定每个组别 i 的均值和总体均值，则 B 的计算公式为：

（3）MANOVA 采用多个统计量来评估组间和组内的差异。最常用的统计量之一是 Wilks' Lambda

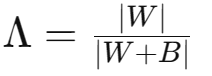
Wilks' Lambda 统计量使用 W 和 B 的协方差矩阵来评估组间和组内的差异。Lambda 的值越接近 0，表示组间差异较大，而 Lambda 的值越接近 1，表示组间差异相对较小。

# 9、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.

建议反馈