# 方差分析

# 1、作用

方差分析（单因素方差分析或 F 检验）用于定类字段（X）与 1 个或 1 个以上的定量字段（Y）之间的差异性研究。需要注意的是，一个定类字段称为单因素方差分析，两个定类字段及以上称为多因素方差分析，与独立样本 T 检验不同的是，方差分析可用于多分类定类字段数据的差异性分析，T 检验只能作用于二分类定类变量。

# 2、输入输出描述

输入：一个定类字段（如受教育程度）、一个或多个定量字段（如工资、家庭年收入）

输出：模型检验的结果：同一因素不同分组（如：不同的受教育程度 X）对定量变量（如：工资 Y）产生/不产生显著性影响

# 3、案例示例

案例：分析个人受教育程度（定类变量）是否给个人的经济收入（定量变量）带来显著性影响

# 4、案例数据

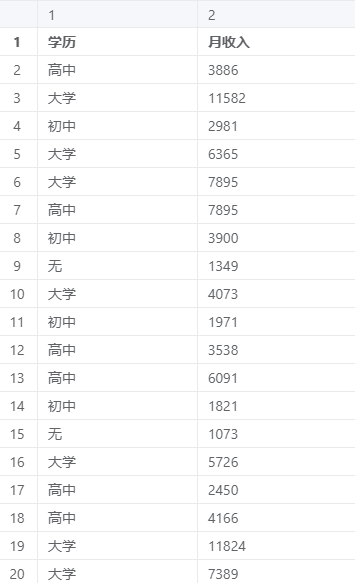
方差分析案例数据

# 5、案例操作

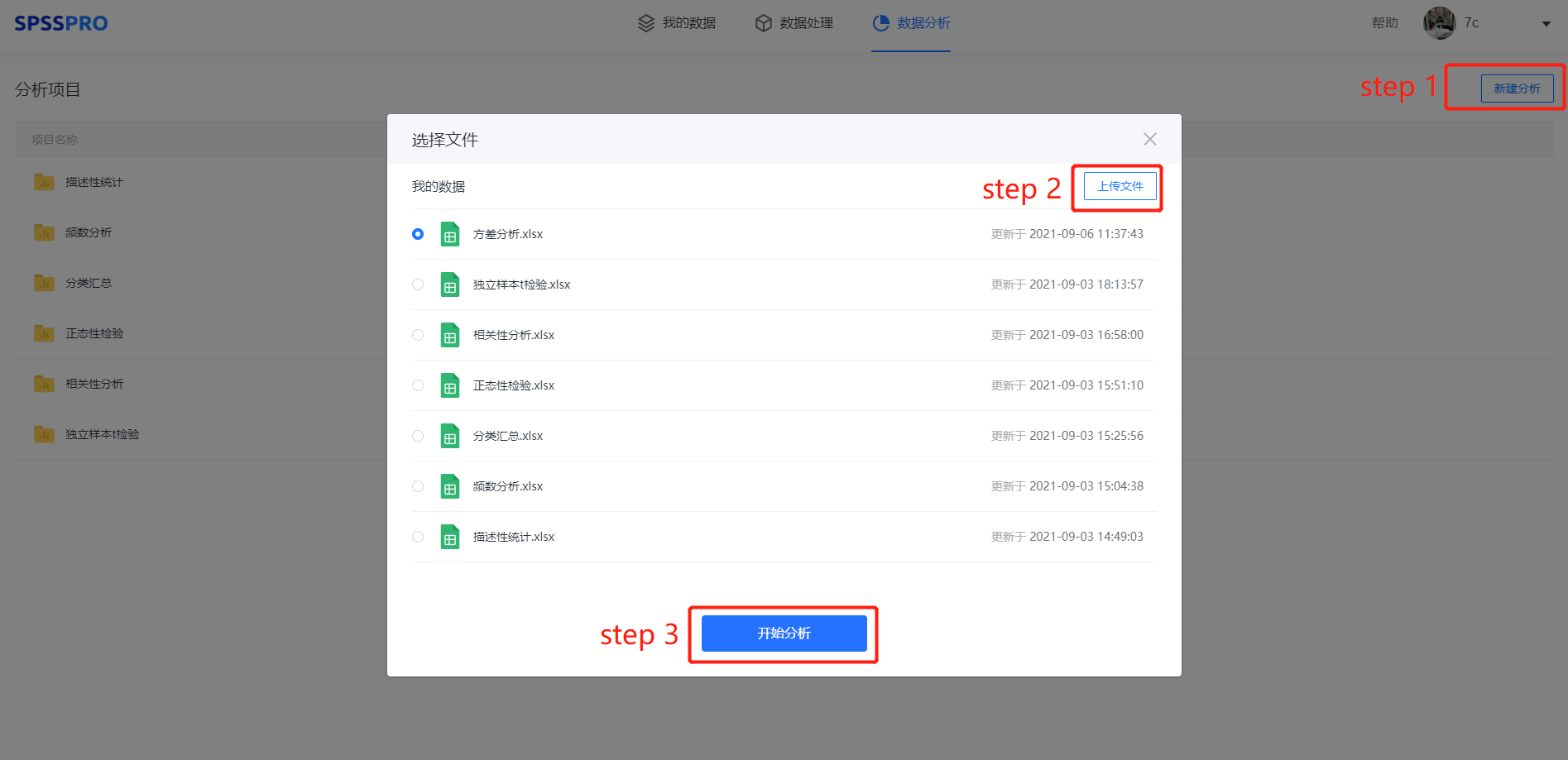
Step1：新建项目；

Step2：上传数据；

Step3：选择对应数据打开后进行预览，确认无误后点击开始分析；

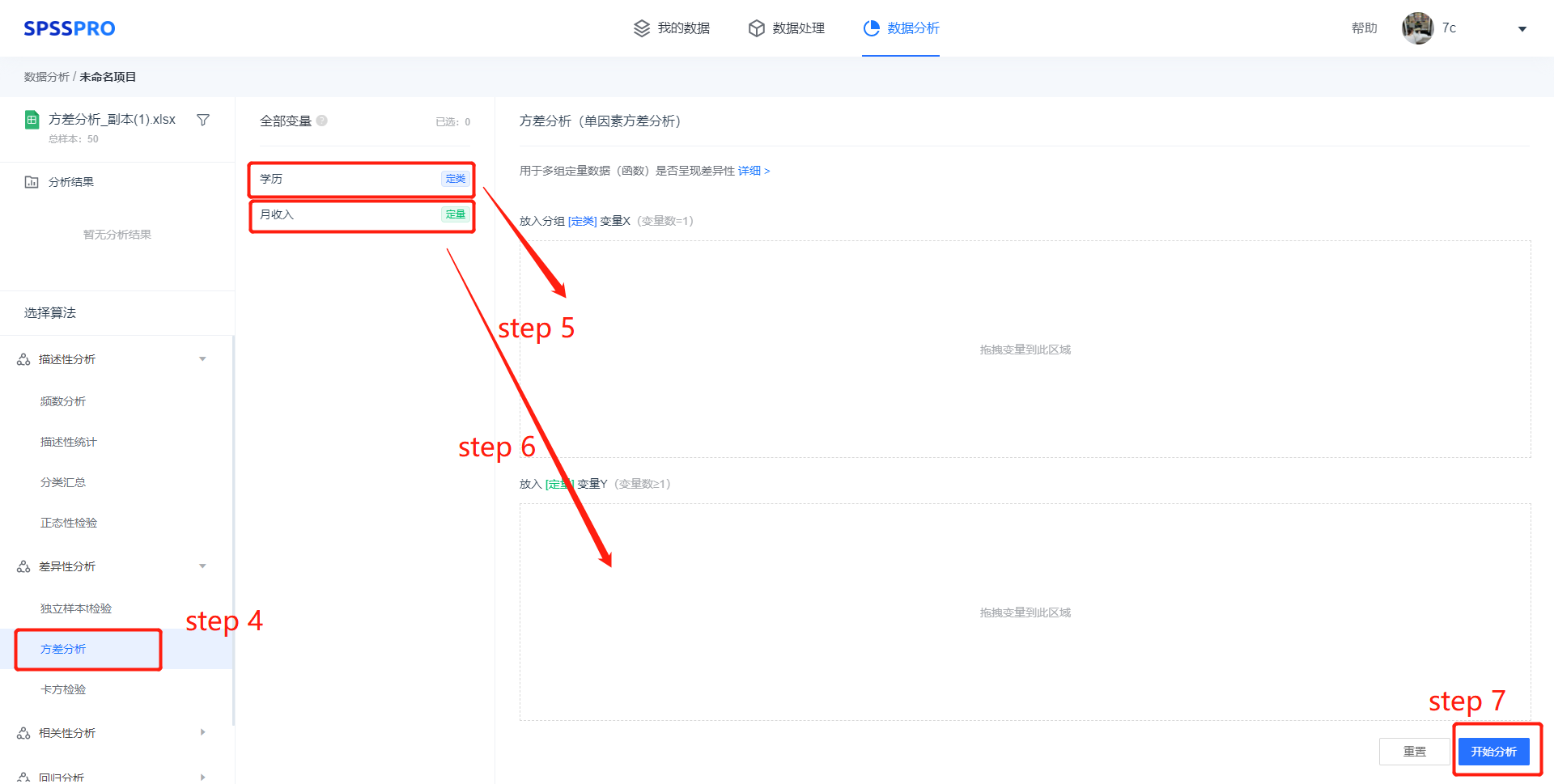
step4：选择【方差分析】；

step5-6：查看对应的数据数据格式，【方差分析】要求输入数据为分组定类变量，变量数=1；放入定量变量，变量数至少为 1 项；

step6：点击【开始分析】，完成全部操作。

# 6、输出结果分析

输出结果 1：正态性检验结果​

变量名	样本量	平均值	标准差	偏度	峰度	S-W 检验	K-S 检验
月收入	50	4959.8	3279.92	0.6	-0.468	0.945(0.022*)	0.116(0.481*)

图表说明​: 上表展示了定量变量月收入描述性统计和正态性检验的结果，包括中位数、平均值等，用于检验数据的正态性。分析项：月收入，样本采用 Shapiro-Wilk 检验，显著性 P 值为 0.022_，水平上呈现显著性，拒绝原假设，因此数据不满足正态分布，其峰度（-0.468）绝对值小于 10 并且偏度（0.6）绝对值小于 3，可以结合正态分布直方图、PP 图或者 QQ 图进行进一步分析，如果分布大致正态化，可以描述为基本符合正态分布。

输出结果 2：正态性检验直方图

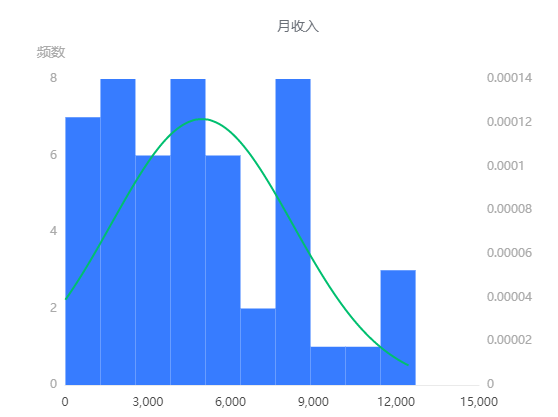
图表说明：上图展示了定量变量月收入数据正态性检验的结果，若正态图基本上呈现出钟形（中间高，两端低）， 则说明数据虽然不是绝对正态，但基本可接受为正态分布。 ​

输出结果 3：方差齐性检验

图表说明：上表展示了方差齐性的结果，包括标准差、F 检验结果、显著性 P 值。方差齐性检验的结果显示，对于时间，显著性 P 值为 0.202*，水平上不呈现显著性，不能拒绝原假设，因此数据满足方差齐性。 ​

输出结果 4：单因素方差分析对比图

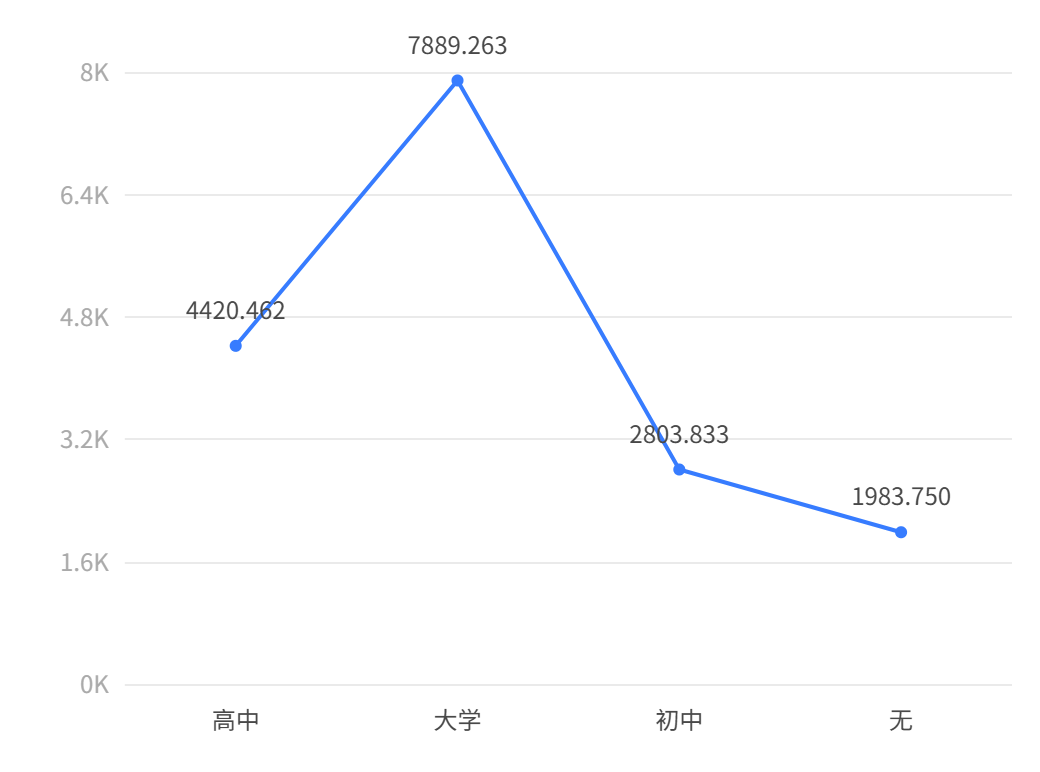
图表说明：上图展示了方差分析的均值的结果，通过比较均值，可以挖掘其差异关系。 ​

输出结果 5：方差分析结果表

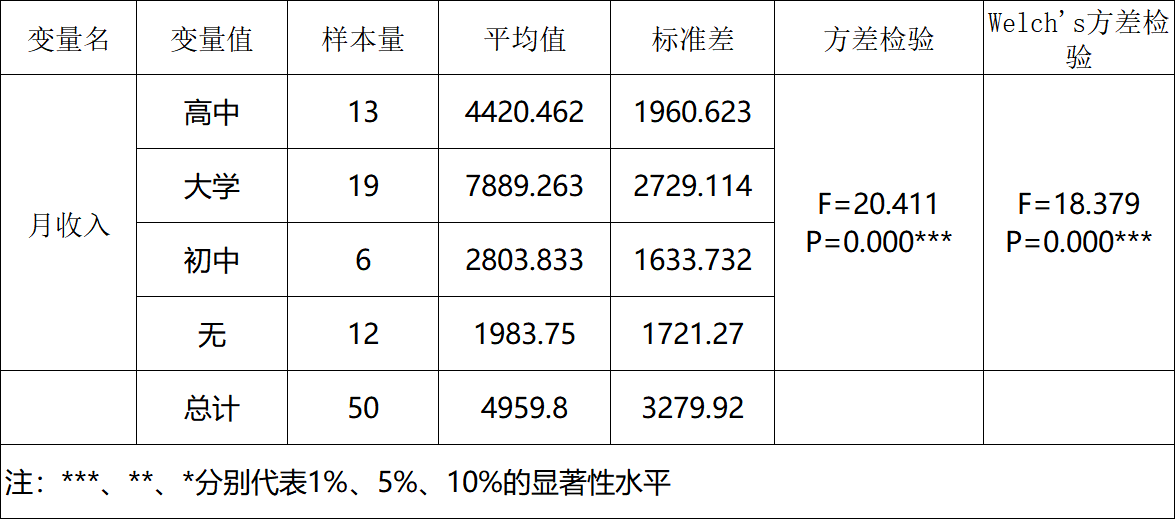
图表说明：上表展示了方差分析的结果，包括均值 ± 标准差的结果、F 检验结果、显著性 P 值。1.0 与 2.0 与 3.0 与 4.0 在月收入上的均值分别为：4420.462、7889.263、2803.833、1983.750；T 检验结果 p 值为 0.000≤0.05，因此统计结果显著，说明 1.0 与 2.0 与 3.0 与 4.0 在月收入上存在显著差异。 ​

输出结果 6：效应量化分析表

分析项	组间差	总离差	偏 Eta 方(Partial η²)	Cohen’s f 值
月收入	301006488.002	527136008.000	0.571	1.154

图表说明：上表展示了效应量化分析的结果，包括组间差异、总差异、偏 Eta 方 η²、Cohen's f 值，用于分析数据间的差异。效应量化分析的结果显示，基于月收入，Eta 方（η² 值）为 0.571，说明数据的差异有 57.1%是来源于不同组别间的差异。Cohen’s f 值为 1.154，说明数据的效应量化的差异程度为大程度差异

# 7、注意事项

• 从理论上方差分析的分析变量（定量变量）Y 需要满足正态性检验与方差齐检验，如果不满足，建议采用非参数多独立样本检验；
• 单因素方差分析与独立样本 T 检验的区别主要在于分析的分组个数，独立样本 T 检验支持 2 个分组，超过三个分组需要采用方差分析，从原理上来说本来 t 检验和 F 检验在公式上推倒上是可以相通的，两个检验的条件都得符合正态性和方差齐性

# 8、模型理论

# 概念

• 因素（条件）：在进行方差分析研究时，所要检验的对象称为因素或条件；
• 水平（处理）：因素对应的不同取值称为水平或处理；
• 观测值：每个因素水平下得到的实验数据称为观 测值。 设因素共有k个水平，而各个水平的均值分别用${\mu }_1,{\mu }_2,{\mu }_3,...,{\mu }_k$表示，要同时检验k个水平（即k个总体）的均值是否相等，需要提出如下假设： - $H_0:H0:{\mu }_1={\mu }_2={\mu }_3=...={\mu }_k$ ，因素对实验结果的影响比随机误 差对实验结果的影响小； - $H_1:{\mu }_1,{\mu }_2,{\mu }_3,...,{\mu }_k$不全相等，因素对实验结果的影响比 随机误差对实验结果的影响大。

# 基本假设

• 线性假定，即模型假定为线性的；
• 各个总体均服从正态分布。对于因素的每一个水平来说，观测值都是来自正态总体的简单随机样本；
• 各个总体的方差$σ^{2} $应相等。对于各组观测数据，它们是具有从相同方差的正态分布中抽取的；
• 观测值是独立的。

# 分析操作步骤

第一步：
提出两种假设（原假设与备择假设）。

• $H_0:{\mu }_1={\mu }_2={\mu }_3=...={\mu }_k$，因素对实验结果的影响比随机误差对实验结果的影响小；
• $H_1:{\mu }_1,{\mu }_2,{\mu }_3,...,{\mu }_k$不全相等，因素对实验结果的影响比随机误差对实验结果的影响大。

如果拒绝原假设$H_0$，说明因素对实验结果的影响比随机误差对实验结果的影响大；
如果不拒绝原假设$H_0$ ，则还没有充分证据证明因素对实验结果的影响比随机误差对实验结果的影响大。
特别指出，当拒绝原假设$H_0$时，所有的总体均值${\mu }_1,{\mu }_2,...,{\mu }_i,...,{\mu }_k$应该至少有两个总体的均值不相等，但不能保证所有的总体均值同时都不相等。

第二步：
选择并且构造检验统计量。 为了检验原假设H0是否成立，需要先选择合适的检验统计量，并且计算检验统计量的值。 分别计算因素在不同水平的均值：
$\overline{x_i}=\frac{\sum _{j=1}^{n_i}{x}_{ij}}{n_i}$
$i=1,2,3,...,k$ ，其中，$n_i$是第i个总体实验数据的个数；
计算全部观测值的总均值：
$\overline{\overline{x_i}}=\frac{\sum _{i=1}^k\sum _{j=1}^{n_i}{x}_{ij}}{n}=\frac{\sum _{i=1}^k{n}_i\overline{x_i}}{n}$

其中，n = n1 + n2 + ... + nk
为了构造检验统计量，首先需要计算3个误差平方和：分别是总误差平方和（SST ）、因素误差平方和（SSA )、 随机误差平方和( SSE )。其计算公式如下：
$SST=\sum _{i=1}^k\sum _{j=1}^{n_i}(x_{ij}-\bar{\overline{x}}{)}^2$
$SSA=\sum _{i=1}^k\sum _{j=1}^{n_i}(\overline{x_i}-\bar{\overline{x}}{)}^2=\sum _{i=1}^k{n}_i(\overline{x_i}-\bar{\overline{x}}{)}^2$
$SSE=SSE=\sum _{i=1}^k\sum _{j=1}^{n_i}(x_{ij}-\overline{x_i}{)}^2$
三者之间存在：
$\sum _{i=1}^k\sum _{j=1}^{n_i}(x_{ij}-\bar{\overline{x}}{)}^2=\sum _{i=1}^k{n}_i(\overline{x_i}-\bar{\overline{x}}{)}^2+\sum _{i=1}^k\sum _{j=1}^{n_i}(x_{ij}-\overline{x_i}{)}^2$
即SST = SSA + SSE
由于三个误差平方和的大小都受到观测数据数目多少的影响，观测值数目越多，计算得到的误差平方和越大。为了消除观测值数目多少对误差平方和计算结果大小的影响，需要用各平方和计算结果除以它们各自所对应的自由度，即是均方。三个自由度分别为: n-1，k-1 与 n-k 。
SSA 的均方也被称为组间均方或组间方差，记为 MSA 。计算公式可以表示为：
$MSA=\frac{\mathrm{组}\mathrm{间}\mathrm{平}\mathrm{方}\mathrm{和}}{\mathrm{自}\mathrm{由}\mathrm{度}}=\frac{SSA}{k-1}$
SSE 的均方也被称为组内均方或组内方差，记为 MSE 。其计算公式为：
$MSE=\frac{\mathrm{组}\mathrm{内}\mathrm{平}\mathrm{方}\mathrm{和}}{\mathrm{自}\mathrm{由}\mathrm{度}}=\frac{SSE}{n-k}$
统计理论已经证明，组间均方与组内均方之比是一个服从F分布的统计量。将 MSA 与 MSE 进行对比，即得到所需要的 F 检验统计量,如下所示。
$F=\frac{MSA}{MSE}\sim F(k-1,n-k)$

第三步：
根据给定的显著性水平α，查F分布表，确定临界值F_α(k-1,n-k)。
根据给定的显著性水平α 、分子（组间均方）自由度$d{f}_1=k-1$ 、分母（组内均方）自由度 $d{f}_2=n-k$ ，查找$F_{\alpha }(k-1,n-k)$，确定相应的临界值。

第四步：
做出统计意义上的决策。 根据计算得到的检验统计量的值F，与查表所得的 临界值$F_{\alpha }(k-1,n-k)$进行比较，做出统计意义上的决策。
若$F>F_{\alpha }$，则拒绝原假设，即$H_0:{\mu }_1={\mu }_2={\mu }_3=...={\mu }_k$的假设不成立，表明因素对实验结果的影响比随机误差对实验结果的影响大；
若$F<F_{\alpha }$，则不能拒绝原假设$H_0$，没有充分的证据证明因素对实验结果的影响比随机误差对实验结果的影响大。
在进行统计决策时，还可以直接利用方差分析表中输出 P值与显著性水平α进行比较，得出结论。

# 9、手推步骤

# Step 1：建立假设

原假设 $H_0$:所有学历的月收入均值相等（${\mu }_{\text{高中}}={\mu }_{\text{大学}}={\mu }_{\text{初中}}={\mu }_{\text{无}}$）。
备择假设 $H_1$:至少有一个学历的月收入均值与其他组不同。

# Step 2：计算各组均值与总均值

根据数据分组计算：

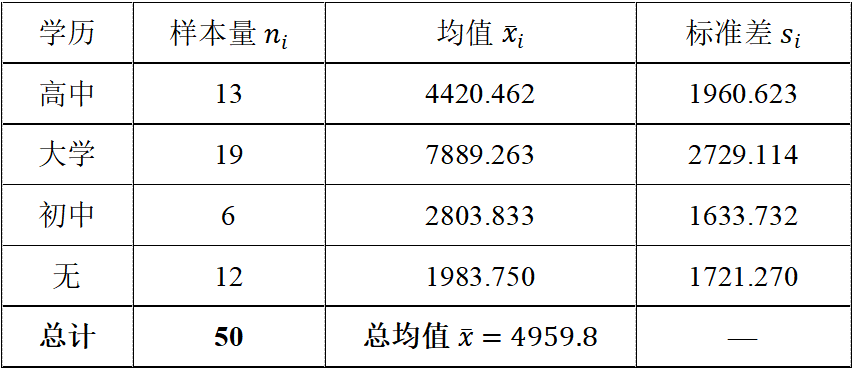
# Step 3：计算平方和

组间平方和（SSA）:

$SSA=\sum n_i({\overline{x}}_i-\overline{x}{)}^2$

计算过程：

• 高中：$13\times (4420.462-4959.8{)}^2=13\times (-539.338{)}^2=3,783,000$
• 大学：$19\times (7889.263-4959.8{)}^2=19\times {2929.463}^2=163,020,000$
• 初中：$6\times (2803.833-4959.8{)}^2=6\times (-2155.967{)}^2=27,888,000$
• 无：$12\times (1983.75-4959.8{)}^2=12\times (-2976.05{)}^2=106,272,000$
• $SSA$ 总和:$3,783,000+163,020,000+27,888,000+106,272,000=300,963,000$

总平方和（SST）:

1.计算数据均值：$\overline{x}=4959.8$
2.求和所有平方差: $SST=\sum _{i=1}^{50}(x_{ij}-4959.8{)}^2=527,136,008$

组内平方和（SSE):

$SSE=SST-SSA=527,136,008-301,006,488.002=226,129,519.998$

# Step 4：计算均方

组间均方（MSA）:

$MSA=\frac{SSA}{k-1}=\frac{301,006,488.002}{4-1}=100,335,496.001$

组内均方（MSE）:

$MSE=\frac{SSE}{n-k}=\frac{226,129,519.998}{50-4}=4,915,859.130$

# Step 5：计算 $F$ 统计量

如下：

$F=\frac{MSA}{MSE}=\frac{100,335,496.001}{4,915,859.130}=20.41$

# Step 6：决策与结论

临界值：查F分布表（$\alpha =0.05,d{f}_1=3,d{f}_2=46$），临界值 $F_{0.05}(3,46)\approx 2.81$。
比较：$F=20.41>2.81$，拒绝原假设 $H_0$。
结论：不同学历的月收入存在显著性差异（$P={0.000}^{\ast \ast \ast }$）。

# Step 7：完整分析结果：

方差分析表：

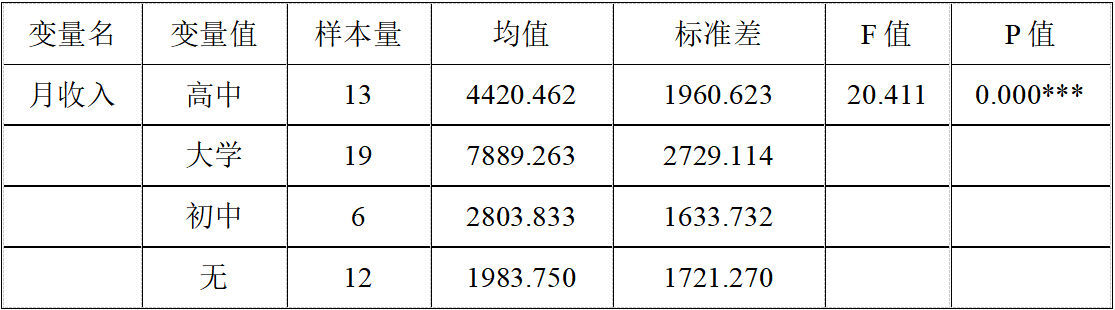
效应量分析：

• 偏Eta方（η²）：0.571（57.1%的差异由学历不同导致）。
• Cohen's f值：1.154（大效应量）。

不同学历对月收入的影响具有统计学显著性（$F=20.41,P<0.001$），且效应量较大（$\eta ²=0.571$）。大学学历的月收入显著高于其他学历。

# 10、参考文献

[1] Scientific Platform Serving for Statistics Professional 2021. SPSSPRO. (Version 1.0.11)[Online Application Software]. Retrieved from https://www.spsspro.com.
[2]戴金辉, 袁靖. 单因素方差分析与多元线性回归分析检验方法的比较[J]. 统计与决策, 2016, No.453(09):23-26.